基于列车车次的动车组运用优化模型与算法

钟庆伟; 张永祥; 王典; 殷勇; 闫旭; 彭其渊

doi:10.3969/j.issn.0258-2724.20191140

基于列车车次的动车组运用优化模型与算法

doi: 10.3969/j.issn.0258-2724.20191140

钟庆伟^1,2,,
张永祥^1,2,
王典^1,2,
殷勇^1,2, ,,
闫旭^1,2,
彭其渊^1,2

基金项目: 国家重点研发计划（2017YFB1200701）；国家自然科学基金（U1834209）

详细信息

作者简介:
钟庆伟（1991—），男，博士研究生，研究方向为运输组织优化理论与方法，E-mail：qingweizhong@my.swjtu.edu.cn

通讯作者:
殷勇（1976—），男，副教授，博士，研究方向为运输组织优化理论与方法，E-mail：yinyong@swjtu.edu.cn

中图分类号: U292.6+2
计量
- 文章访问数: 743
- HTML全文浏览量: 239
- PDF下载量: 52
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-11
- 修回日期: 2020-03-01
- 网络出版日期: 2021-03-09
- 刊出日期: 2021-04-15

Optimization Model and Algorithm for Train-Set Scheduling Based on Trip Sequence

ZHONG Qingwei^{1,2
,},
ZHANG Yongxiang^1,2,
WANG Dian^1,2,
YIN Yong^{1,2
, ,},
YAN Xu^1,2,
PENG Qiyuan^1,2

摘要

摘要: 动车组运用计划的编制通常需要综合考虑运输安全、效率及成本等多方面因素，其编制质量及编制效率对高速铁路运营有重要影响. 为了快速获得高质量动车组运用计划，以降低综合运营成本和总空驶里程等为优化目标，建立了基于列车车次的可改编动车组运用优化混合整数线性规划模型，并设计了一个迭代逼近算法框架. 该算法框架将整个问题分解为主问题和子问题，其中主问题的最优解为整个问题提供有效下界，而主问题可行解集合中能够通过子问题检验的解为整个问题提供有效上界，从而算法框架可以不断地更新上、下界之间的最优间隙，迫使生成更接近于下界的新可行解. 多个实例分析表明：所提出的方法与人工方法相比，能够快速生成动车组运用计划，且使得动车组综合运营成本平均下降10.5%，总空驶里程平均减少23%.
- 高铁网络 /
- 动车组运用优化 /
- 改编 /
- 维修约束 /
- 迭代逼近算法
Abstract: Usually, the train-set schedule involves several practical aspects, such as operational safety, efficiency, and cost. The quality and efficiency of the schedule have a significant impact on the operation of high-speed railways. In order to quickly obtain a high-quality train-set schedule, a mixed-integer linear programming (MILP) model that takes composition changes on the basis of the trip sequences was established with the optimization goals of reducing operating costs and total deadhead mileages. Furthermore, an iterative gap reducing algorithm is developed to solve the MILP model, which divides the whole problem into the master problem and sub-problem. The master problem provides an effective lower bound for the whole problem, and its solutions that can pass the sub-problem provide an effective upper bound for the whole problem. As a result, the algorithm can continuously reduce the gap between bounds and generate a new feasible solution towards the lower bound. The real cases show that compared with the manual method, the proposed method can generate a high quality one-day train-set schedule in a short time, which reduces the total operating costs by 10.5% and the total deadhead mileage by 23%.
- high-speed rail network /
- train-set scheduling /
- composition changes /
- maintenance constraints /
- iterative gap reducing algorithm

HTML全文

图 1 列车时刻表及站间距信息

Figure 1. Information of timetable and interval of stations

下载: 全尺寸图片幻灯片

图 2 3种可行的动车组运用计划方案示例

Figure 2. Three kinds of possible train-set scheduling

下载: 全尺寸图片幻灯片

图 3 基于路径生成的迭代逼近算法流程

Figure 3. Flow chart of iterative gap reducing algorithm

下载: 全尺寸图片幻灯片

图 4 测试的高铁路网络结构

Figure 4. Tested high-speed railway network

下载: 全尺寸图片幻灯片

图 5 不同策略下目标函数值收敛过程示意

Figure 5. Convergence process of objective function value process under different scenarios

下载: 全尺寸图片幻灯片

表 1 动车组单元基本量信息

Table 1. Basic information of EMUs

动车编号	动车类型	累积时间/min	累积里程/km
1	AL	1 440	800
2	AL	1 440	800
3	AL	0	0
4	AL	0	0
5	A	1 440	2 000
6	A	1 440	2 000
7	A	0	0
8	A	0	0

下载: 导出CSV

表 2 各动车所不同类型的动车组单元保有量信息

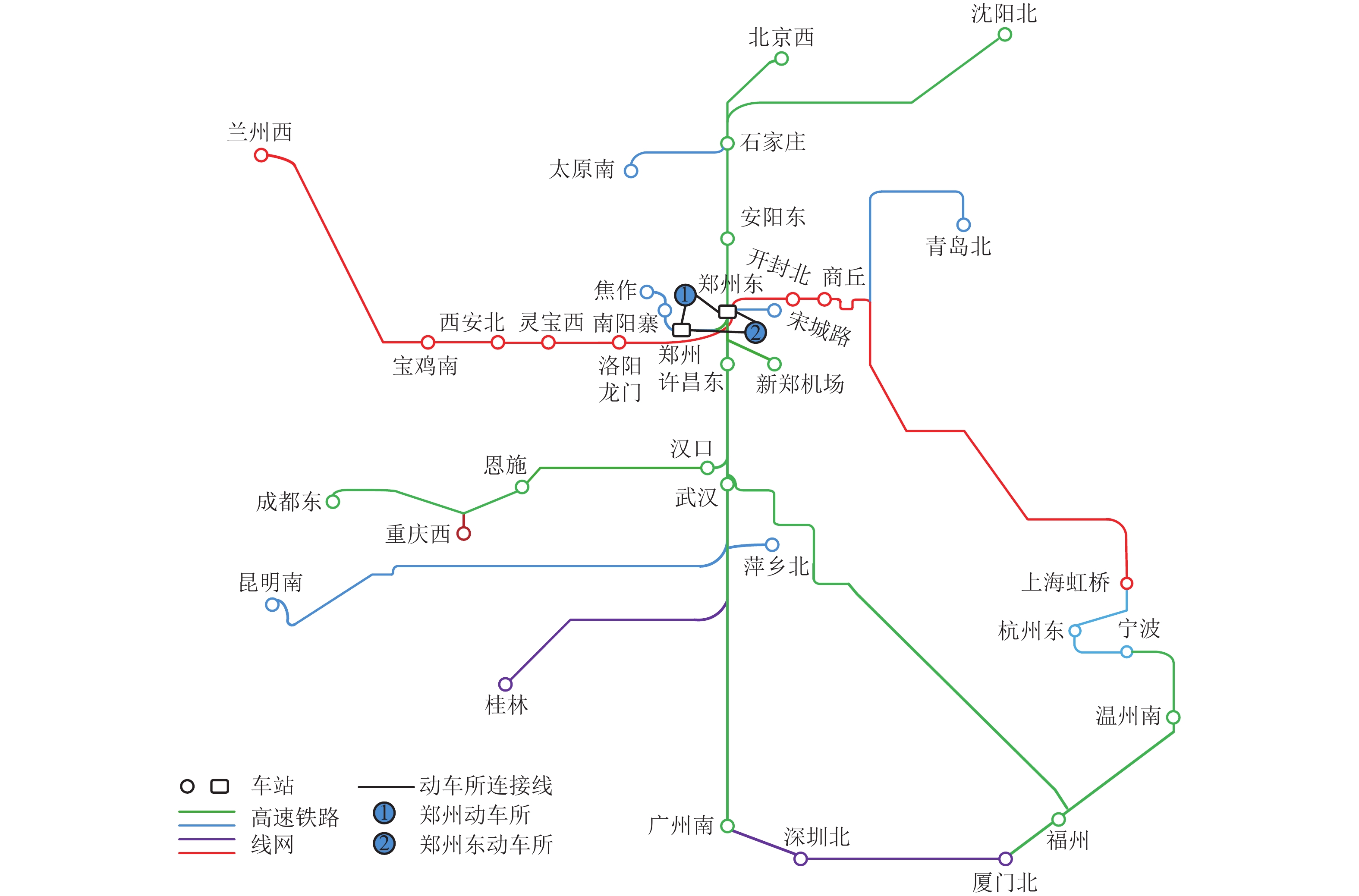
Table 2. Information of EMUs for different depots 组

数据	动车所	380AL	380A	380B	6A
数据 1	郑州	0	7	11	0
数据 1	郑州东	36	9	28	0
数据 2	郑州	0	0	0	8
数据 2	郑州东	34	16	40	0

下载: 导出CSV

表 3 不同策略下各案例的动车运用计划关键技术指标

Table 3. Key statistics of train-set scheduling cases under different scenarios

数据	运营策略	方案	RS/km	ARL/km	MRL/km	MARL/km	AERL/km	ERL/km	OP/组	OBJ/元	OBJ^SP/元	CT/s
数据 1	策略 1	下界	53	2577.7	509	4771	61.7	3273	13	110053	735117	13
		算法	53	2577.7	509	4771	61.7	3273	13	110053	742809	108
		人工	57	2435	183	4898	92.8	5291	13	124471	745915
	策略 2	下界	51	2678.0	320	5419	63.7	3247	13	109727	705117	17
	策略 2	算法	51	2678.0	320	5419	63.7	3247	13	109727	705117	17
数据 2	策略 1	下界	66	2720.0	554	5316	72.2	4765	18	145862	916365	20
		算法	66	2720.4	324	5188	72.8	4804	18	145904	903375	120
		人工	70	2575.7	571	5229	74.8	5240	18	160753	945812
	策略 2	下界	65	2760.8	660	5316	72.9	4736	18	145336	888375	22
	策略 2	算法	65	2760.8	631	5434	72.9	4736	18	145536	894313	120
注：人工方案并未统计具体的编制时间.

下载: 导出CSV

参考文献(16)

彭其渊,李建光,杨宇翔,等. 高速铁路建设对我国铁路运输的影响[J]. 西南交通大学学报,2016,51(3): 525-533. doi: 10.3969/j.issn.0258-2724.2016.03.011

PENG Qiyuan, LI Jianguang, YANG Yuxiang, et al. Influences of high-speed railway construction on railway transportation of China[J]. Journal of Southwest Jiaotong University, 2016, 51(3): 525-533. doi: 10.3969/j.issn.0258-2724.2016.03.011

尹深, 曾伟. 全国铁路今起实行新的列车运行图. [EB/OL]. 人民网, （2019-04-10）[2019-04-10]. http://society.people.com.cn/n1/2019/0410/c1008-31021820.html? utm_source=UfqiNews

ABBINK E, BERG B V D, KROON L, et al. Allocation of railway rolling stock for passenger trains[J]. Transportation Science, 2004, 38(1): 33-41. doi: 10.1287/trsc.1030.0044

ALFIERI A, GROOT R, KROON L, et al. Efficient circulation of railway rolling stock[J]. Transportation Science, 2006, 40(3): 378-391. doi: 10.1287/trsc.1060.0155

FIOOLE P J, KROON L, MARÓTI G, et al. A rolling stock circulation model for combining and splitting of passenger trains[J]. European Journal of Operational Research, 2006, 174(2): 1281-1297. doi: 10.1016/j.ejor.2005.03.032

MARÓTI G, KROON L. Maintenance routing for train units:the transition model[J]. Transportation Science, 2005, 39(4): 518-525. doi: 10.1287/trsc.1050.0116

GÁBOR M, LEO K. Maintenance routing for train units:the interchange model[J]. Computers & Operations Research, 2007, 34(4): 1121-1140.

史峰,周文梁,郁宇卫,等. 客运专线动车组运用计划优化模型与算法[J]. 铁道学报,2011,33(1): 1-13. doi: 10.3969/j.issn.1001-8360.2011.01.001

SHI Feng, ZHOU Wenliang, YU Yuwei, et al. Optimized model and algorithm of motor trains-sets scheduling for dedicated passenger lines[J]. Journal of the China Railway Society, 2011, 33(1): 1-13. doi: 10.3969/j.issn.1001-8360.2011.01.001

赵鹏,富井规雄. 基于路段交换的多基地动车组运用计划的编制算法[J]. 铁道学报,2004,26(1): 7-11. doi: 10.3321/j.issn:1001-8360.2004.01.002

ZHAO Peng, NORIO Tomii. An algorithm for multiple-bases train-set scheduling based on path-exchange[J]. Journal of the China Railway Society, 2004, 26(1): 7-11. doi: 10.3321/j.issn:1001-8360.2004.01.002

王莹,刘军,苗建瑞. 基于列生成算法的动车组检修计划优化[J]. 中国铁道科学,2010,31(2): 115-120.

WANG Ying, LIU Jun, MIAO Jianrui. Column generation algorithms based optimization method for maintenance scheduling of multiple units[J]. China Railway Science, 2010, 31(2): 115-120.

李建,林柏梁,耿令乾,等. 基于交路接续的动车组运用计划优化模型与算法[J]. 交通运输系统工程与信息,2015,15(5): 172-177,194.

LI Jian, LIN Boliang, GENG Lingqian, et al. Optimizaiton model and algorithm for motor trainset utilization scheduling based on routes connection[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(5): 172-177,194.

LI J, LIN B, WANG Z, et al. A pragmatic optimization method for motor trainset assignment and maintenance scheduling problem[J]. Discrete Dynamics in Nature & Society, 2016(3): 1-13.

BORNDÖRFER R, REUTHER M, SCHLECHTE T, et al. Integrated optimization of rolling stock rotations for intercity railways[J]. Transportation Science, 2016, 50(3): 863-877. doi: 10.1287/trsc.2015.0633

高博, 曹国厂. 我国首列可变编组动车组已具备出厂条件[EB/OL]. 新华网, （2019-02-25）[2019-02-25]. http://www.gd.xinhuanet.com/newscenter/2019-02/25/c_1124157073.htm

殷勇,陈锦渠,朱蔓,等. 城市轨道交通站点失效修复策略[J]. 西南交通大学学报,2020,55(4): 865-872.

YIN Yong, CHEN Jinqu, ZHU Man, et al. Repair strategies for failure of urban rail transit stations[J]. Journal of Southwest Jiaotong University, 2020, 55(4): 865-872.

ZHONG Q, LUSBY R M, LARSEN J, et al. Rolling stock scheduling with maintenance requirements at the Chinese high-speed railway[J]. Transportation Research Part B: Methodological, 2019, 126: 24-44.

施引文献

附加材料(0)

访问统计