Optimization Research on Mixed-Model Multi-manned Assembly Line Balancing Problem of Type I
-
摘要: 针对使用传统模型和算法求解第一类多人共站混流装配线的平衡问题,兼顾工作站数、工人数和工作站负荷均衡,引入了新变量和不对称约束来构建新的数学模型. 提出了一种改进的鸡群算法,使用基于优先权值的编码方式在解码过程中优先选择能最早开始作业的工人来减少序列相关空闲时间,设定工位分配接受准则来分配工人数量以减少工位平均空闲时间;根据适应值大小将种群分为3个不同的群体来实现系统的有效搜索,其中,公鸡群个体基于其适应值差异在不同大小的邻域范围内搜索,母鸡群个体基于适应值相关的参数分别向所归属的公鸡或者其他公鸡/母鸡方向搜索,小鸡群个体则向其归属的母鸡方向搜索;最后将新模型和改进的鸡群算法用于求解标杆算例. 研究结果表明:在算例验证中,对比传统的模型,新模型多找出8个算例的最优解,且寻优速度更快;在算法平均收敛运算时间相似的情况下,本文所提算法求得的平均工人数、工位数以及平滑指标系数等评价指标分别提高了10.74%、16.05%和44.89%,验证了所提模型和算法的有效性和优越性.Abstract: Owing to the incapability of the traditional approaches in solving the mixed-model multi-manned assembly line balancing problem of type I (MMALBP-I), a new mixed integer mathematical model is built to minimize the number of stations/workers and to balance the load between stations by introduce new variants and unequal constraints. What’s more, a modified chicken swarm optimization is also proposed. The algorithm adopts a priority-based coding and in decoding procedure, a worker which the assigned task can start earlier is being selected to reduce the sequence-dependent idle time, and the number of workers is decided by the designed station assignment rules to rude the mean station idle time. Moreover, in order to achieve more systematic and efficient search, the chicken swarm is divided into three groups according to the fitness values of the chickens themselves. The roosters generate new solution by a local search in different range of places based on the fitness value, the hens follow their group-mate roosters or other chickens to search a new solution based on the fitness value, the chicks move around their mother hens to update themselves. The proposed approaches are applied to solve the standard test instances. The results show that compared with the old model, the optimal results of eight more instances are found in the new mode in less time. The performance of the three evaluation indicators obtained using the proposed algorithm are improved by 10.74%, 16.05%, 44.89%, respectively, within the approximate time. Thus, above results verify the effectiveness and superiority of the proposed model and algorithm.
-
表 1 符号含义
Table 1. Meaning of the notations
符号 描述 $ n $ 总的作业数量 $ {S}_{\rm{max}} $ 最大的工位数量 $ {M}_{\rm{max}} $ 总的模型数量 $ {W}_{\rm{max}} $ 每个工位允许分配的最大的工人数量 $ i,h $ 作业序号 $ j $ 工位序号 $ m $ 模型序号 $ k $ 工人序号 $ {C}_{\rm{T}} $ 节拍 $ \psi $ 一个很大的数 $ \vartheta $ 一个很小的数 $ I $ 作业集合$({1,2},3,\cdots ,\;n)$ $ J $ 工位集合${({1,2},3,\cdots ,\;S}_{\rm{max} })$ $ M $ 模型集合$({1,2},3,\cdots,\; {M}_{\rm{max} })$ $ K $ 工人集合${({1,2},3,\cdots, \;W}_{\rm{max} })$ $ P\left(i\right) $ 作业 i 的全部直接前序 ${P}_{{\rm{a}}} \left(i\right)$ 作业 i 的全部前序 $ S\left(i\right) $ 作业 i 的全部直接后序 $ {S}_{\rm{a}}\left(i\right) $ 作业 i 的全部后序 $ {t}_{im} $ 作业 i 在模型 m下的作业时间 $ {T}_{im} $ 如果 tim大于0,则 Tim为1;否则为 0 $ {t}_{{\rm{s}},im} $ 作业 i 在模型 m下的开始时间 $ {w}_{ik} $ 如果作业 i 分配给工人 k 为 1;否则为 0 $ {s}_{ij} $ 如果作业 i 分配给工位 j 为 1;否则为 0 $ {w}_{{\rm{u}},jk} $ 如果工人 k 分配给工位 j 为 1;否则为 0 $ {s}_{{\rm{u}},j} $ 如果开启工位 j,则为 1;否则为 0 $ {y}_{ih} $ 如果作业 i 分配在作业 h 的前面为 1;否则为 0 表 2 测试数据集特征
Table 2. The feature of test data sets
ID 问题 n $ {M}_{\rm{max}} $ $ {W}_{\rm{max}} $ ${T}_{\rm{min} }$ ${T}_{\rm{max} }$ In1 Mertens 7 2 2 1 5 In2 Bowman 8 2 2 2 17 In3 Jaeschke 9 2 2 1 6 In4 Jackson 11 2 2 1 7 In5 Mansoor 11 2 2 2 44 In6 Mitchell 21 2 2 1 12 In7 Heskia 28 2 2 2 115 In8 Sawyer 30 2 2 1 24 In9 Kilbridge 45 2 2 1 54 In10 Tong 70 2 2 1 170 In11 Arcus 83 2 2 23 3 899 In12 Arcus 111 2 2 6 5 712 表 3 模型对比结果
Table 3. Model comparison results
ID $ {C}_{\rm{T}} $ 模型 1 模型 2 $ {N}_{{\rm{s}}}\left({N}_{\rm{w}}\right) $ G/% t/s $ {N}_{{\rm{s}}}\left({N}_{\rm{w}}\right) $ G/% t/s In1 6 4(6) 0 < 1.0 4(6) 0 < 1.0 7 3(6) 0 2.6 3(6) 0 < 1.0 8 3(5) 0 < 1.0 3(5) 0 < 1.0 10 3(4) 0 < 1.0 3(4) 0 < 1.0 15 2(3) 0 < 1.0 2(3) 0 < 1.0 18 1(2) 0 < 1.0 1(2) 0 < 1.0 In2 17 5(6) 0 < 1.0 5(6) 0 < 1.0 21 4(5) 0 < 1.0 4(5) 0 < 1.0 24 4(4) 0 < 1.0 4(4) 0 < 1.0 28 3(3) 0 < 1.0 3(3) 0 < 1.0 31 2(3) 0 < 1.0 2(3) 0 < 1.0 In3 6 5(8) 0 < 1.0 5(8) 0 < 1.0 7 5(8) 0 < 1.0 5(8) 0 < 1.0 8 5(7) 0 < 1.0 5(7) 0 < 1.0 10 4(4) 0 < 1.0 4(4) 0 < 1.0 18 2(3) 0 < 1.0 2(3) 0 < 1.0 In4 7 6(9) 0 33.0 6(9) 0 < 1.0 9 4(6) 0 15.0 4(6) 0 < 1.0 10 4(6) 0 23.0 4(6) 0 < 1.0 13 3(5) 0 105.0 3(5) 0 < 1.0 14 3(4) 0 11.0 3(4) 0 < 1.0 21 2(3) 0 3.9 2(3) 0 < 1.0 In5 45 3(5) 0 15.0 3(5) 0 < 1.0 54 3(4) 0 3.3 3(4) 0 < 1.0 63 3(4) 0 13.4 3(4) 0 < 1.0 72 2(3) 0 1.3 2(3) 0 < 1.0 81 2(3) 0 1.6 2(3) 0 < 1.0 In6 14 10(14) 32 ~ 10(14) 0 2.5 15 9(13) 42 ~ 9(13) 0 2.0 21 5(7) 52 ~ 5(7) 0 < 1.0 26 5(6) 64 ~ 5(6) 0 < 1.0 35 3(4) 0 782.0 3(4) 0 < 1.0 39 3(4) 0 1 938.0 3(4) 0 < 1.0 In7 138 21(9) 77 ~ 5(8) 0 27.2 205 28(7) 86 ~ 3(6) 0 719.0 216 5(6) 83 ~ 3(5) 0 19.5 256 3(5) 80 ~ 3(5) 20 ~ 324 4(4) 75 ~ 2(4) 0 197.0 342 2(4) 75 ~ 2(4) 25 ~ 表 4 算法对比结果
Table 4. Comparison results of algorithms
ID ${ {{C} }_{\rm{T} } }$ ${ {{L} }_{\rm{B} } }$ SA ICSO ${{N} }_{ {\rm{s} } }\left({{N} }_{\rm{w} }\right)$ ${{L} }_{\rm{E} }$ ${ {{S} } }_{\rm{I} }$ ${{N} }_{ {\rm{s} } }\left({\rm{N} }_{\rm{w} }\right)$ ${{L} }_{\rm{E} }$ ${ {{S} } }_{\rm{I} }$ t/s 最佳值 平均值 最佳值 平均值 最佳值 平均值 最佳值 平均值 最佳值 平均值 最佳值 平均值 In10 184 19 12(22) 12.9(23.3) 84.99 79.75 31.61 45.07 12(21) 12(21.4) 89.04 87.42 23.35 26.48 258.0 364 10 6(11) 6.5(11.8) 85.93 80.20 61.32 87.18 6(11) 6.0(11.0) 85.93 85.93 46.68 52.32 128.0 410 9 5(10) 5.9(10.6) 83.91 79.46 66.14 99.69 5(9) 5.0(9.9) 93.24 84.85 34.27 58.02 107.0 468 8 5(9) 5.0(9.5) 81.68 77.60 86.53 121.80 4(8) 4.9(8.1) 91.89 90.87 39.43 46.85 165.0 527 7 4(8) 4.3(8.0) 81.61 81.61 101.3 114.80 4(8) 4.0(8.0) 81.61 81.61 64.45 75.59 199.0 In11 5048 16 11(19) 12.0(19.4) 78.88 75.76 1295 1522.00 10(18) 10.1(18.4) 83.26 81.51 960.90 1221.00 81.8 5853 14 10(16) 10.1(16.8) 80.79 76.62 1295 1670.00 9(15) 9(15) 86.17 86.17 790.20 937.00 89.7 6842 12 8(14) 8.3(14.1) 78.98 76.88 1527 1895.00 8(13) 8(13) 85.06 84.45 1057.00 1176.00 118.0 7571 11 7(12) 7.6(12.9) 83.27 77.05 1514 2134.00 7(11) 7(11.1) 90.85 90.09 703.00 818.8 79.1 8412 10 6(11) 6.9(11.7) 81.76 77.20 1695 2252.00 6(11) 6(11) 81.76 81.76 1460.00 1518 94.4 8998 9 6(10) 6.2(10.7) 84.08 76.69 1844 2663.00 6(10) 6(10) 84.08 84.08 1380.00 1447 113.0 10816 8 5(8) 5.1(8.8) 87.44 77.14 1720 2993.00 5(8) 5(8) 87.44 87.44 1410.00 1509 112.0 In12 5755 27 18(32) 19.3(32.6) 82.71 76.62 1249 1497.00 16(29) 16.2(29.4) 91.26 90.05 589.50 726.5 403.0 8847 18 12(22) 13.0(22.4) 86.08 76.88 1754 2830.00 11(19) 11(19.6) 90.61 87.89 915.60 1461 447.0 10027 16 11(18) 11.2(19.7) 79.95 77.05 2669 3298.00 10(17) 10(17.2) 89.35 88.36 1343.00 1589 377.0 10743 15 10(17) 11.0(18.8) 78.77 77.20 3189 3556.00 9(16) 9(16.3) 88.61 87.11 1450.00 1936 376.0 11378 14 9(16) 9.6(16.8) 83.67 76.69 2444 3429.00 8(15) 8(15.4) 89.24 87.01 1683.00 2206 345.0 17067 9 6(11) 6.1(11.2) 81.13 77.14 3911 4810.00 5(10) 5.9(10) 89.24 89.24 2167.00 2387 252.0 表 5 对比结果汇总
Table 5. The summary of comparison results
算法 g1% g2% LE SI 平均值 最佳值 Db Dc 平均值 最佳值 Db Dc 平均值 最佳值 平均值 最佳值 SA 19.88 14.33 0.66 0.72 31.24 23.06 0.50 0.39 73.56 79.38 965.34 730.70 ICSO 9.14 7.71 0.15 0.19 15.19 14.02 0.06 0.03 82.88 83.06 531.06 446.47 差值 10.74 6.62 0.51 0.53 16.05 9.04 0.44 0.36 −9.32 −3.68 434.28 284.23 -
CEVIKCAN E, ASLAN D, YENI F B. Disassembly line design with multi-manned workstations:a novel heuristic optimisation approach[J]. International Journal of Production Research, 2020, 58(3): 649-670. doi: 10.1080/00207543.2019.1587190 潘志豪,郭宇,查珊珊,等. 基于混合优化算法的飞机总装脉动生产线平衡问题[J]. 计算机集成制造系统,2018,24(10): 64-75.PAN Zhihao, GUO Yu, ZHA Shanshan, et al. Aircraft pulsating assembly line balancing problem based on hybrid algorithm[J]. Computer Integrated Manufacturing Systems, 2018, 24(10): 64-75. SIVASANKARAN P, SHAHABUDEEN P. Literature review of assembly line balancing problems[J]. The International Journal of Advanced Manufacturing Technology, 2014, 73(9): 1665-1694. 李大双,张超勇,邵新宇,等. 基于殖民竞争算法的多约束双边装配线平衡[J]. 机械工程学报,2015,51(2): 183-189. doi: 10.3901/JME.2015.02.183LI Dashuang, ZHANG Chaoyong, SHAO Xinyu, et al. Hybrid colonial competitive algorithm for the two-sided assembly line balancing problem with mutiple constraints[J]. Journal of Mechanical Engineering, 2015, 51(2): 183-189. doi: 10.3901/JME.2015.02.183 刘俨后,左敦稳,张丹. 随机作业时间的装配线平衡问题[J]. 计算机集成制造系统,2014,20(6): 1372-1378.LIU Yanhou, ZUO Dunwen, ZHANG Dan. Assembly line balancing with stochastic operation times[J]. Computer Integrated Manufacturing Systems, 2014, 20(6): 1372-1378. 詹慧文,罗亚波,潘玉玲,等. 基于混合蝙蝠算法的多约束双边装配线平衡问题研究[J]. 工业工程与管理,2019,24(1): 16-23.ZHAN Huiwen, LUO Yabo, PAN Yulin, et al. A study on two-sided assembly line balancing problem with multiple constraints based on hybrid bat algorithm[J]. Industrial Engineering and Management, 2019, 24(1): 16-23. DIMITRIADIS S G. Assembly line balancing and group working:a heuristic procedure for workers’ groups operating on the same product and workstation[J]. Computers & Operations Research, 2006, 33(9): 2757-2774. doi: 10.1016/j.cor.2005.02.027 KELLEGOZ T. Assembly line balancing problems with multi-manned stations:a new mathematical formulation and Gantt based heuristic method[J]. Annals of Operations Research, 2017, 253(1): 377-404. doi: 10.1007/s10479-016-2156-x MICHELS A S, LOPES T C, SIKORA C G S, et al. A Benders’ decomposition algorithm with combinatorial cuts for the multi-manned assembly line balancing problem[J]. European Journal of Operational Research, 2019, 278(3): 796-808. doi: 10.1016/j.ejor.2019.05.001 KELLEGÖZ T, TOKLU B. An efficient branch and bound algorithm for assembly line balancing problems with parallel multi-manned workstations[J]. Computers & Operations Research, 2012, 39(12): 3344-60. doi: 10.1016/j.cor.2012.04.019 ŞAHIN M, KELLEGÖZ T. Balancing multi-manned assembly lines with walking workers:problem definition,mathematical formulation,and an electromagnetic field optimisation algorithm[J]. International Journal of Production Research, 2019, 57(20): 6487-6505. doi: 10.1080/00207543.2019.1566672 CHEN Y Y, CHENG C Y, LI J Y. Resource-constrained assembly line balancing problems with multi-manned workstations[J]. Journal of Manufacturing Systems, 2018, 48: 107-119. doi: 10.1016/j.jmsy.2018.07.001 ROSHANI A, GHAZI NEZAMI F. Mixed-model multi-manned assembly line balancing problem:a mathematical model and a simulated annealing approach[J]. ASSEM Autom, 2017, 37(1): 34-50. doi: 10.1108/AA-02-2016-016 NADERI B, AZAB A, BOROOSHAN K. A realistic multi-manned five-sided mixed-model assembly line balancing and scheduling problem with moving workers and limited workspace[J]. International Journal of Production Research, 2019, 57(3): 643-661. doi: 10.1080/00207543.2018.1476786 MENG X, LIU Y, GAO X, et al. A new bio-inspired algorithm: chicken swarm optimization[C]//Proc. of the Advances in Swarm Intelligence. Hefei: Springer, 2014: 86-94. -




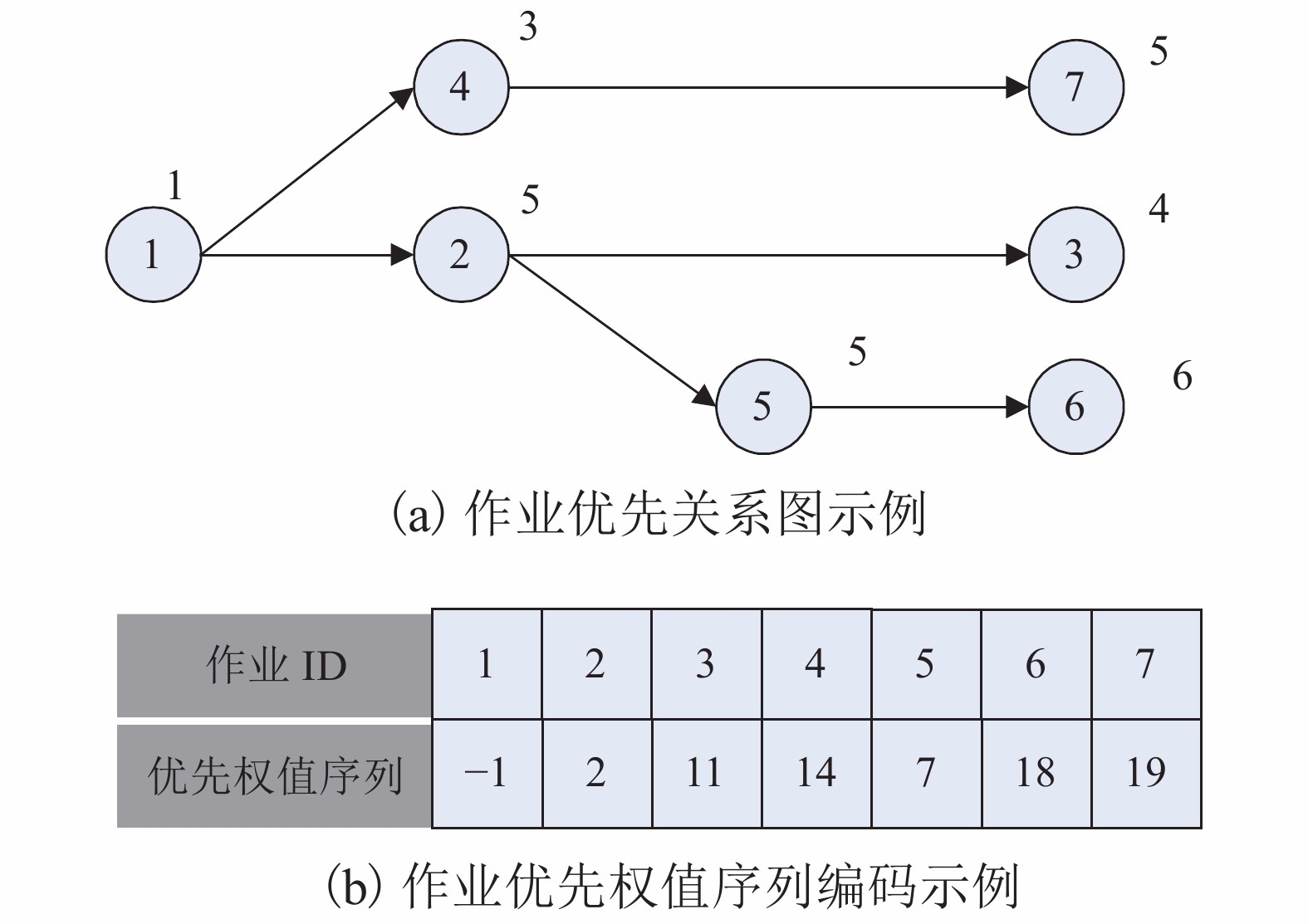
 下载:
下载:

