Spatial Distribution Characteristics of Dynamic Displacement of Heavy-Haul Railway Subgrade System under Launching Impact Load
-
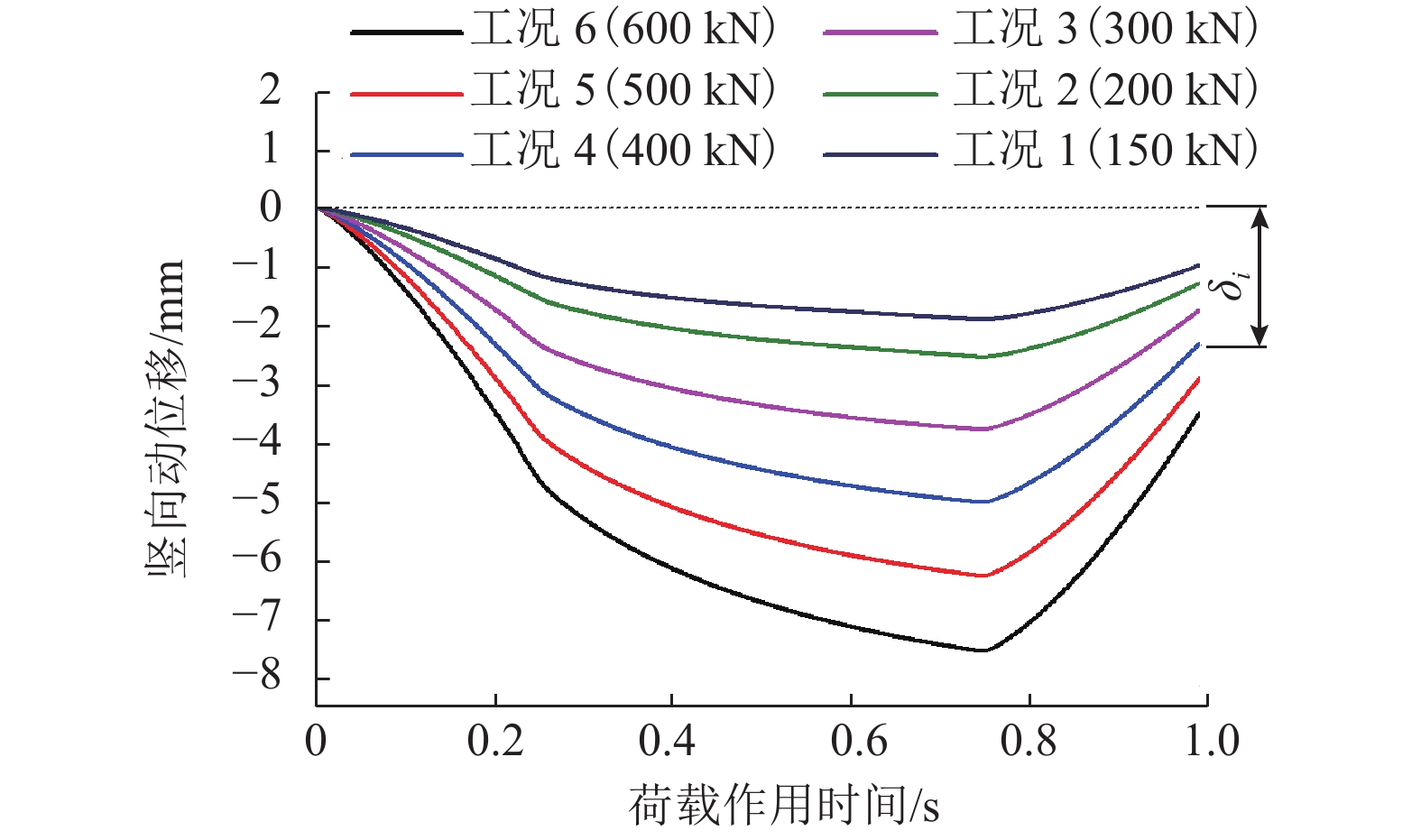
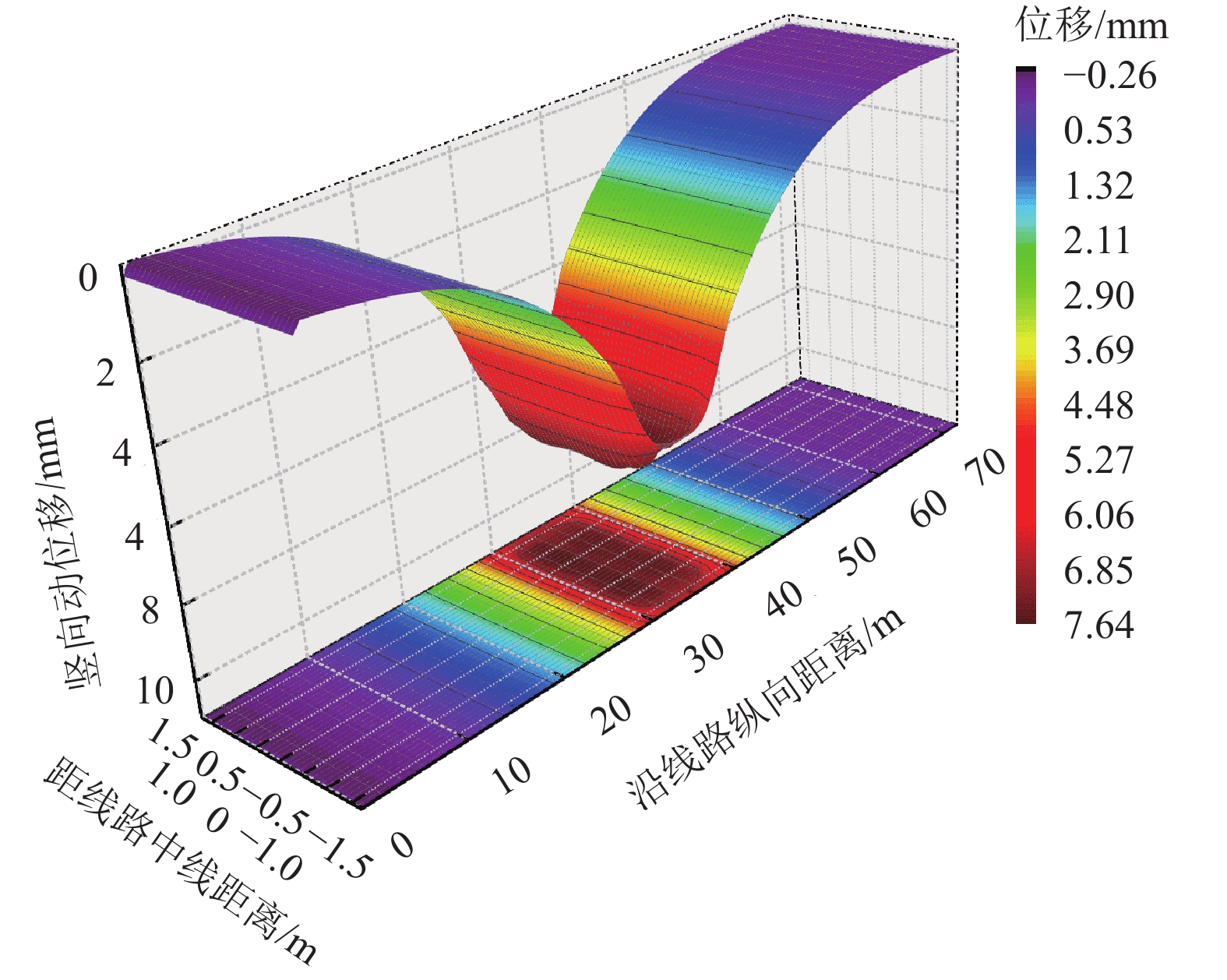
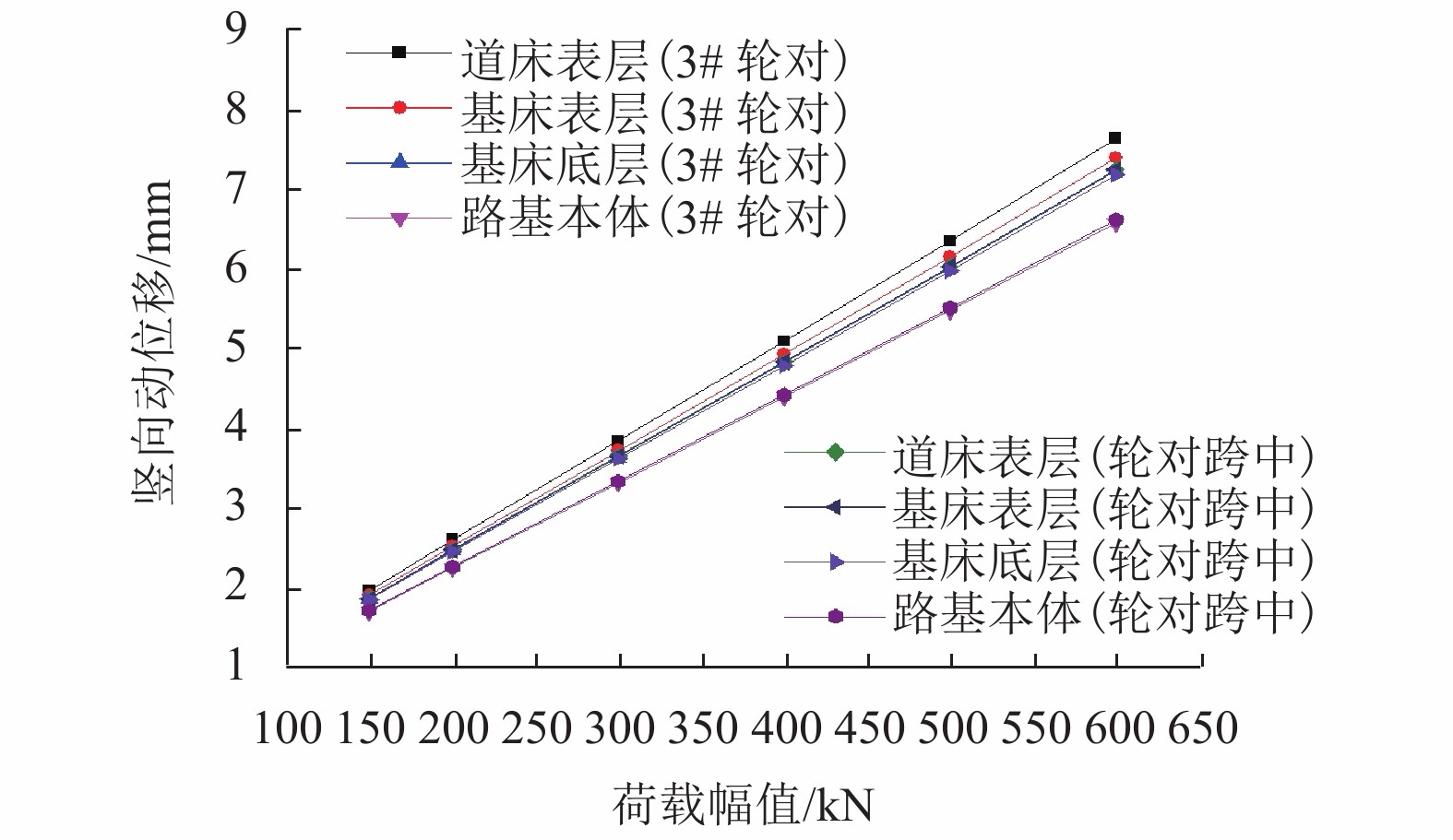
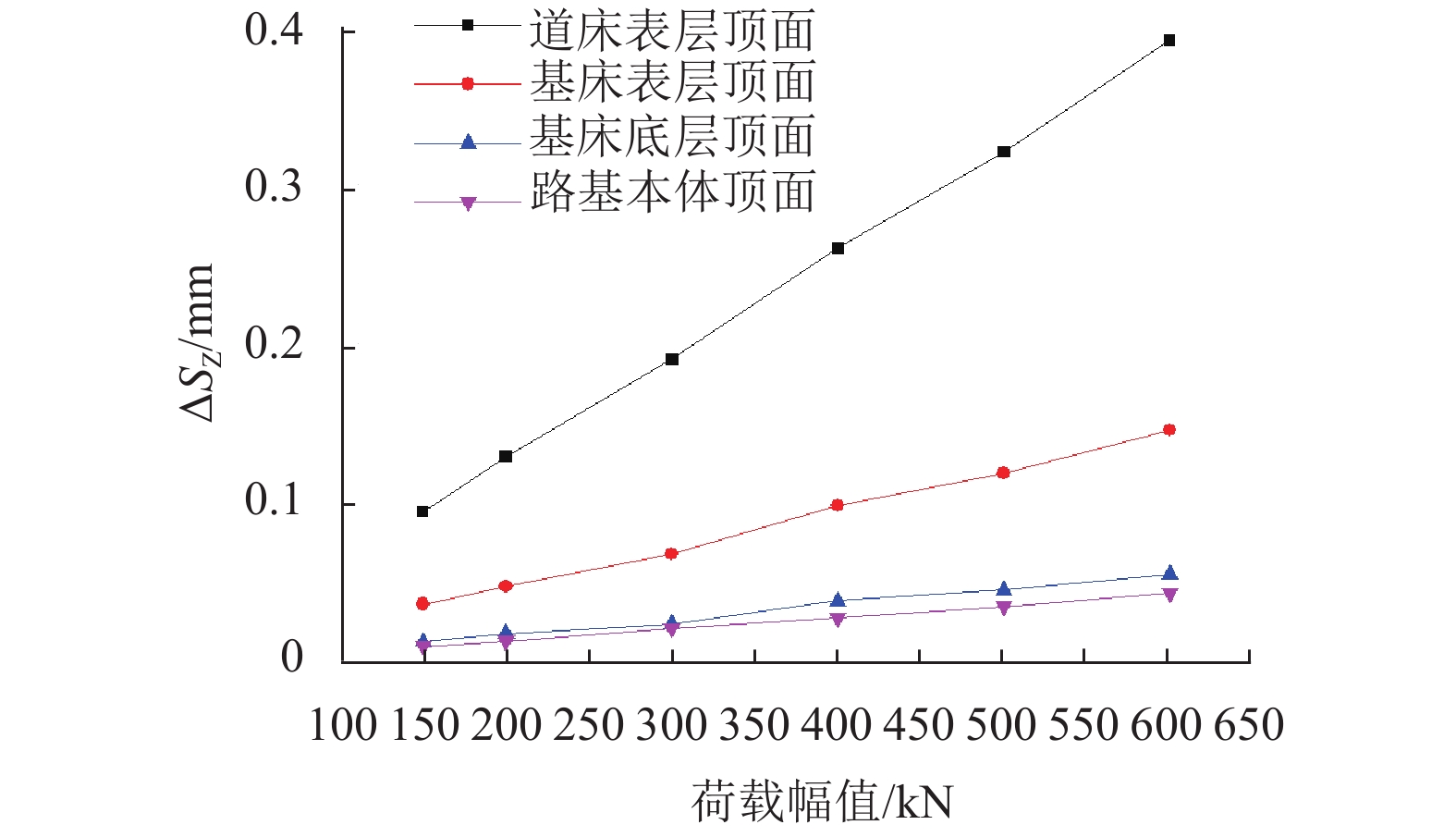
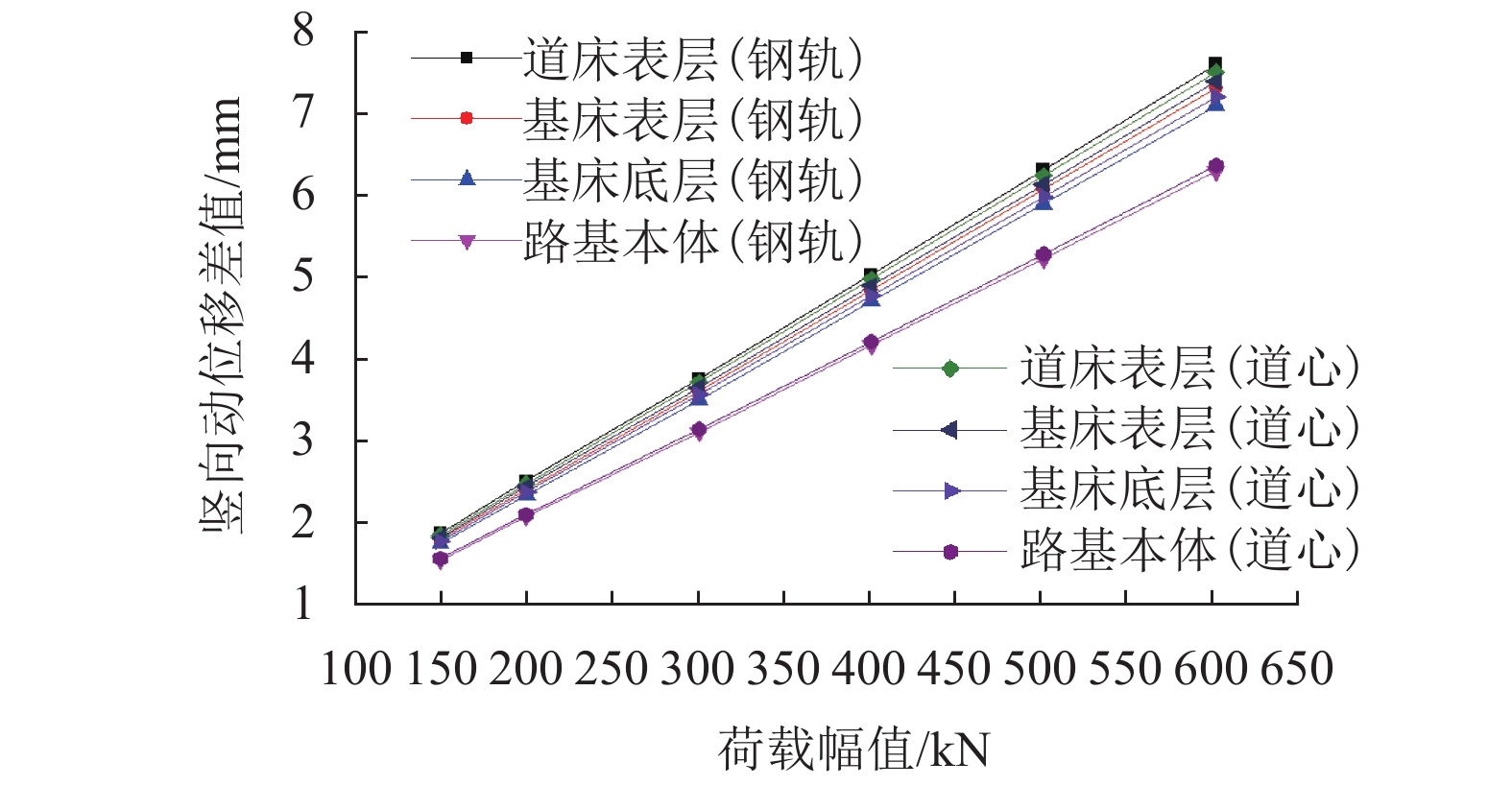
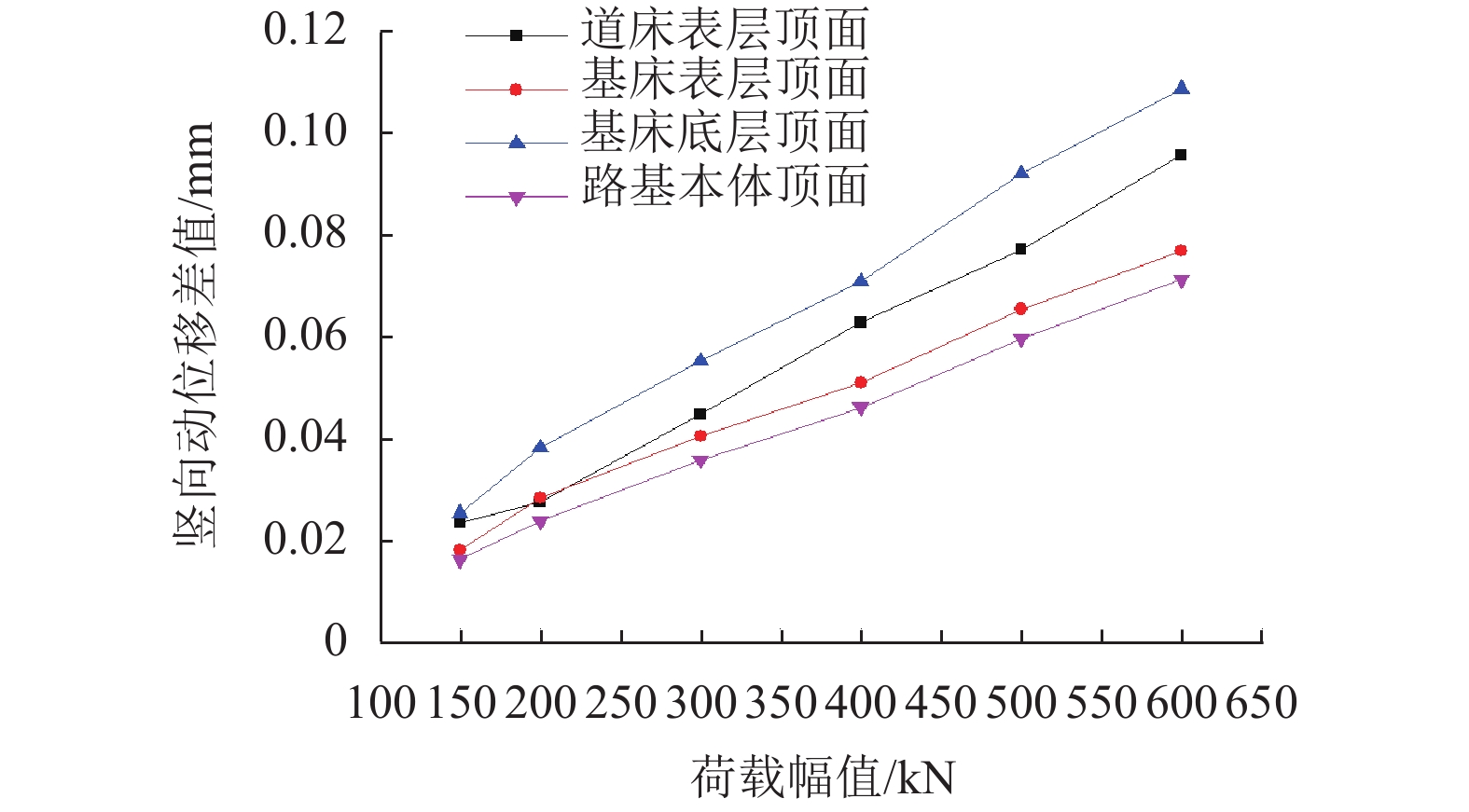
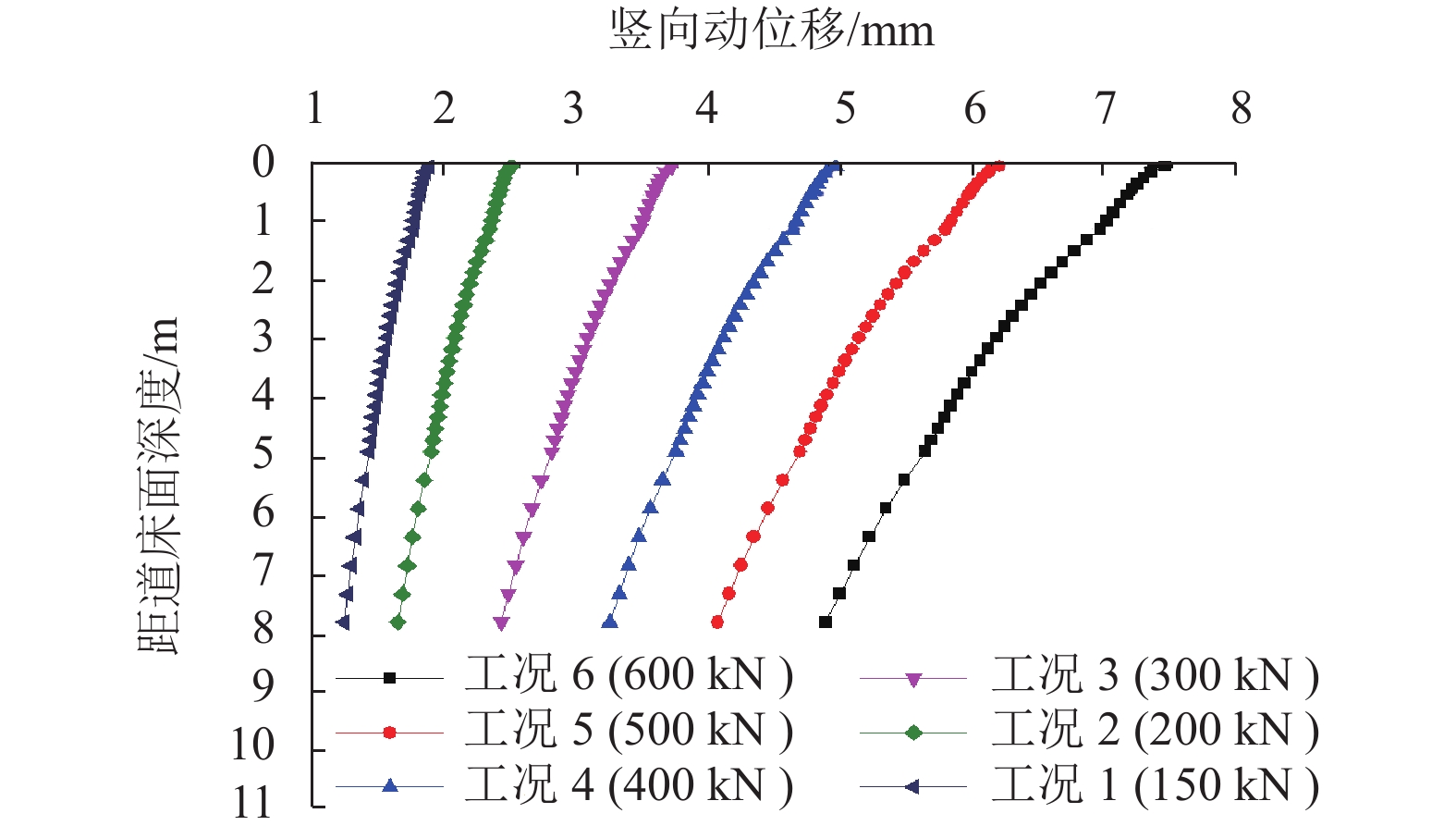
摘要: 为研究军用重载铁路路基动响应空间分布特征，通过高度非线性分析程序ANSYS/LS-DYNA3D建立了重载铁路轨道-路基-地基三维显式动力分析模型，并引入三维一致黏弹性人工边界；采用梯形冲击荷载模拟弹射冲击，探讨了不同幅值(150～600 kN)的弹射冲击荷载作用时重载铁路路基系统动位移的空间分布特征，通过Boussinesq弹性理论与林绣贤多层系统当量理论验证了数值模型的可靠性. 结果分析表明：当作用在轨道上的弹射荷载开始进入卸载状态时，路基系统的竖向动位移达到最大值；结束卸载时，道床顶面存在一定量的残余变形，且残余变形随荷载幅值增长呈线性增长，增长速率约为0.60 × 10−2 mm/kN；在不同荷载幅值下路基动位移沿线路横、纵向均呈对称分布，动位移沿竖向近似呈直线型衰减，且衰减速率随着荷载幅值的增加而增大；荷载幅值越大，路基动位移的轮对效应及道床和基床对钢轨动力的分担作用均越来越显著；路基的动位移峰值与荷载幅值大致呈线性关系，道床顶面的动位移峰值随荷载幅值增长最快，增长速率约为1.27 × 10−2 mm/kN，基床表层与基床底层次之，增长速率分别约为1.23 × 10−2、1.20 × 10−2 mm/kN，路基本体增长最慢，增长速率约为1.10 × 10−2 mm/kN.Abstract: To study the spatial distribution characteristics of dynamic response of military heavy-haul railway subgrade, using highly nonlinear analysis program ANSYS/LS-DYNA3D, a 3D explicit dynamic model of a track-subgrade-foundation system was established with the 3D consistent viscous-spring artificial boundary. The trapezoidal impulse load was used to simulate the launching impact load, and spatial distribution characteristics of the dynamic displacement of the subgrade system under loads of different amplitudes (150−600 kN) were discussed. The model reliability was then verified by Boussinesq elastic theory and Lin Xiuxian ’s multi-layer system equivalent theory. The results indicated that the vertical dynamic displacement of the subgrade system reaches the maximum value when the launching impact load on the track starts to unload. At the end of unloading, there is a certain amount of residual deformation in the top surface of the ballast bed, and the residual deformation increases linearly with an increase in load amplitude, and the growth rate is about 0.6 × 10−2 mm/kN. Under different load amplitudes, the dynamic displacement of the subgrade system is distributed symmetrically both laterally and longitudinally along the line, it decays linearly along the vertical direction, and the decaying rate increases with the increase of the load amplitude. The larger the load amplitude is, the more significant the wheelset effect of dynamic displacement and the contribution of ballast bed and subgrade bed to rail dynamic force are; the peak dynamic displacement of subgrade system is approximately linear with the load amplitude. With the increase of the load amplitude, the peak dynamic displacement of the ballast bed surface grows at the fastest rate of about 1.27 × 10−2 mm/kN, followed by the peak value of the subgrade bed surface and the subgrade bed bottom at growth rates of about 1.23 × 10−2 and 1.20 × 10−2 mm/kN, respectively, and the peak value of the subgrade body grow at the slowest rate of about 1.10 × 10−2 mm/kN.
-
随着基础设施建设的推进，公路与铁路工程建设中为了保证线路的顺直，越来越多的隧道衬砌结构工程穿行大型滑坡区域，形成滑坡-隧道相互作用、相互影响的工程特征[1]，隧道衬砌结构势必会承受滑坡推力作用，当滑坡作用力足够大时，隧道衬砌结构会产生相应变形或破坏.
目前，国内外对这种滑坡-隧道相互作用的特征及机理投入了较多关注，主要表现在三方面，一是对滑坡-隧道相互作用模型体系进行了总结与归纳，如吴红刚等[2]从滑面与隧道相处位置出发，建立了以平行体系、正交体系和斜交体系为核心的较为完备的受力变形模式；张鲁新等[3]分析了滑坡与隧道变形特征并提出五种地质结构模型；陈小云等[4]对于正交体系下隧道与滑带相交力学模型进行了研究. 二是采用多种手段研究了滑坡作用下隧道衬砌结构受力机理以及滑坡-隧道相互作用机理，如陶志平[5]采用室内模型试验方法，分析了滑坡地段隧道的变形机理，研究了隧道围岩和隧道衬砌压力的变化规律；毛坚强等[6]运用接触面来模拟滑面，应用有限元算法分析了滑坡-隧道间的相互作用机理以及隧道的受力变形规律；陈刚[7]分别讨论了隧道开挖和降雨作用对滑坡体变形的影响；王旭[8]结合具体的工程实例，考虑隧道与滑面相对位置关系变化，计算了边坡的安全系数和隧道衬砌结构变形. 同时，国外一部分学者[9-14]确定了隧道在滑坡应力作用下的变形机理，并采用现代传感、监测新技术对滑坡-隧道模型进行研究. 另一部分学者[15-19]通过二维和三维数值模拟方法探讨隧道开挖诱发深部滑坡问题及隧道-滑坡相互作用机理. 特别地，Chiu等[20]通过隧道衬砌变形情况来反应滑坡作用下隧道所受作用力. 第三方面是滑坡-隧道治理措施上开展了卓有成效的研究，如杜升涛[21]通过选用抗滑桩支挡和排水工程综合治理的方案治理襄渝线赵家塘隧道滑坡；陶志平等[22]采用抗滑桩来治理滑坡地段隧道的变形问题；郑颖人等[23]以重庆某高速公路隧道出口段的滑坡治理工程为背景，采用有限元强度折减法研究了滑动面位置与抗滑桩位置和桩间距的关系. 总体来说，目前治理方式一般应用滑坡治理措施和隧道加固措施的原则，主要采用预应力锚索和抗滑桩等来治理滑坡，围岩注浆和增强隧道衬砌等方式来加固隧道，如赣龙铁路马蹄径隧道[24]和相田二号隧道[25]等. 虽然以上研究得了一定的成果，但所有研究主要依托于某一具体滑坡-隧道相互作用案例开展相关滑坡稳定性、隧道变形机理或治理措施相关的研究，还没有出现专门探讨滑坡滑带角度变化对隧道衬砌结构受力变化及对衬砌结构影响的相关研究.
因此，本文采用室内模型试验、数值模拟的方法，探讨针对不同滑带角度条件滑坡作用对隧道衬砌结构受力的影响，得到滑坡作用下偏压隧道衬砌受力[26]变化规律，这对于弥补滑坡-隧道相互作用研究的不足，更加清楚的掌握滑坡作用下隧道衬砌结构受力的变化有一定的现实意义.
1. 滑坡隧道室内模型试验设计
1.1 滑坡隧道工程实例
通过分析国内多个典型滑坡-隧道特征[1, 4, 26-28]可以得出，滑坡滑动带的倾角基本在0°～50°，破坏点基本位于拱脚处. 因此，以下研究主要以大（同）准（格尔）铁路K20南坪隧道为研究原型，考虑不同滑带角度作用下隧道衬砌结构受力变化特征及变化规律. 大（同）准（格尔）铁路K20南坪隧道洞顶回填区为宽缓平台，平台高程为1 205～1 207 m，宽43～77 m. 其地形、岩性结构剖面如图1. 其滑带与隧道夹角约为10°.
南坪隧道受滑坡影响变形较为严重，裂缝多位于拱壁墙边，以纵向为主最长达28 m. 在16～18避车间变形最大实测最大累计变形达24 mm （2016年1月14日—2016年5月1日），工务段实测最大累计变形达77 mm （2015年3月14日— 4月13日）. 避车洞墙边位移过大，导致水沟挤压变形：K20 + 082～K20 + 058段水沟被挤压扭曲，隧道表面混凝土面层产生脱落现象，位移量达28 cm；K20 + 41～K20 + 58段水沟受挤压，盖板鼓起，位移量达6 cm，在与滑带相交处产生了较大的局部剪切变形.
1.2 模型试验相似比
以南坪滑坡隧道为原型，几何比设为1∶100，将重要的滑坡体参数容重γ、黏聚力c、内摩擦角φ根据相似材料进行配比，隧道衬砌弹性模量E以及泊松比μ按照一定的比例进行配置. 按照相似比理论，各变量对应的相似比为CL=100，Cγ=1，Cμ=Cc=Cφ=1，Cσ=CE= 100，其中L为几何尺寸，σ为应力.
1.3 模型试验设计与制作
根据几何相似比，试验模型长2.5 m，宽0.5 m，高0.9 m，如图2. 滑带厚度为3.0 cm，滑动区为滑动面的角度分别设为0°、10°、20°、30°、40°、50°. 滑带材料采用黏性土加少量石膏，滑体由砾石粉粒分层压实组成，使其参数满足相似比要求. 滑床采用中等风化碎石同少量黏土石灰混合、夯实，以减少实验时不必要的沉降变形. 试验材料参数如表1.
表 1 模型试验材料力学参数Table 1. Mechanical parameters of model materials名称 密度 ρ/
（kg•m−3）E/MPa c/kPa φ/（°） 滑坡体 1 900 18.65 27.79 25.35 滑带 1 800 9.36 15.82 15.63 滑床 2 200 23.72 54.24 54.32 隧道衬砌 2 100 289.61 236.65 61.71 在滑体内部放置一长0.5 m、厚1.0 cm的石膏材料隧道. 模型隧道按照模型尺寸订做模具，模具材料为2.0 cm厚的PVC塑料板，并用螺杆穿起拼装为整体，隧道衬砌内模由两块弧形钢板拼成. 模具组装前，先在模具内铺设间距12.0 mm钢丝网，用螺杆拼接，采用石膏∶水＝2∶1比例进行隧道整体浇筑，形成模型试验用隧道结构.
模型试验按滑带角度0°、10°、20°、30°、40°、50° 分别制作相应模型进行试验，即一种滑带角度模型试验完成后，重新制作模型，进行下一种滑带角度模型试验.
1.4 测点布置
滑坡体表面设置位移计监测加载过程中位移变形情况（如图2）. 为了能够详细掌握不同滑带角度作用下隧道衬砌结构应力变化，内外分别布置20个应变片测点（N1～N20、W1～W20），如图3（a）所示. 在隧道横截面布置10个粘贴应变花的测点（J1～J10）监测隧道衬砌受剪情况（图3（b））. 微型压力盒（1～7）布置在隧道衬砌的外侧，用以监测隧道衬砌受到的滑坡推力或压力变化（图3（c））. 同时，为得到隧道衬砌结构上竖向压应力值，采用应变片的方法采集数据，应变片黏贴位置与图3（c）一致（图中未画出）.
1.5 加载方案
根据滑坡隧道演化规律，采用多级加载. 详细的装载方案见表2. 荷载施加在滑坡隧道模型的后缘. 在第一阶段，施加的荷载为500 N，保持20 min. 第二阶段施加1 000 N的荷载，并保持40 min. 从第三阶段到第六阶段，在20 min的时间间隔内平稳地增加了荷载，然后保持40 min，这一过程一直持续到滑坡模型破坏失效.
表 2 模型试验加载方案Table 2. Loading scheme in model test滑带角度/（°） 荷载/kN 加载时
间/min维持时
间/min0、10、20、30、40、50 0.5 10 20 1.0 10 20 5.0 20 40 10.0 20 40 15.0 20 40 20.0 30 40 25.0 30 40 1.6 试验结束标准
经过多次预试验及参考已有模型试验成果，模型试验结束标准选为坡体从隧道顶部滑出，同时加载测力计数值下降，此时判定为模型破坏、失效. 除坡体位移监测外，其他监测元件数据采用测力计为最大值时的监测值作为最终计算数据.
2. 模型试验结果与分析
2.1 模型试验破坏特征
依次开展了滑带角度为0°、10°、20°、30°、40°、50° 的滑坡隧道模型试验. 试验结束后，坡体产生两条裂缝，滑坡产生较大位移，隧道顶部的坡体（坡脚处）基本滑移出模型槽. 隧道顶部坡体表层位移监测点的位移如图4. 随着加载时间的推移，位移逐渐增长，滑带角度为0° 时，模型破坏时位移达到160 mm，滑带角度为50° 时，模型破坏时位移约10 mm. 可以看出：滑带角度越小，坡体变形越大，滑带角度越大，坡体变形越小. 另外，在模型加载初始阶段，滑带小角度变形增长最快，有突然增大过程，但滑带角度达到30° 以后，坡体位移初始阶段增长较慢. 同时，在滑坡推力作用下，隧道衬砌结构产生一定程度的变形，并且隧道衬砌结构相对于原位置产生了一定的位移，0° 时隧道所产生的位移最大约为10 mm，30° 时产生约4 mm的变形，50° 时几乎未产生位移. 可以得到，随着滑带角度的增大，在相同滑坡推力作用下，隧道的变形逐渐减小.
图 4 不同滑带角度条件下坡体位移Figure 4. Displacements of slope with various angles of sliding zone2.2 隧道衬砌结构受力特征
1） 弯矩与剪应力特征
根据图3中隧道衬砌结构上的应变片等测试元件，按照一定的关系式可以计算不同滑带角度下作用于隧道衬砌结构上的应力与弯矩值，如表3.
表 3 不同滑带角度下隧道弯矩与剪应力值Table 3. Bending and shear stress values of tunnel under different angles of sliding zone滑带角度/（°） 弯矩/（kN•m） 剪力/kN 0 
10 
20 
30 
40 
50 
从表3中可以看出：对于隧道衬砌结构上所受弯矩，滑带角度0° 时弯矩最大值为463 kN•m（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）弯矩值为201 kN•m，左右两侧弯矩相差2.3倍，两侧受力不均，形成典型偏压隧道. 滑带角度30° 时，弯矩最大值为178 kN•m（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）弯矩值为65 kN•m，左右两侧弯矩相差2.7倍. 当滑带角度50° 时，弯矩最大值为87 kN•m（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）弯矩值为27 kN•m，左右两侧弯矩相差3.2倍. 可见，弯矩在靠山侧的拱脚处达到最大值，最大值随着滑带角度的增大而减小，并且随滑带角度越大，在相同滑坡推力作用下隧道衬砌结构上所受弯矩越小.
对于隧道衬砌结构上所受剪力，基本与弯矩规律类似. 滑带角度 0° 时剪力最大值为20.3 kN（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）剪力值为18.5 kN. 滑带角度30° 时，剪力最大值为16.8 kN（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）剪力值为5.7 kN. 当滑带角度50° 时，剪力最大值为7.3 kN（图3（c）点3），对应的隧道另一侧测点（图3（c）点6）剪力值为2.9 kN. 可见，剪力在靠山侧的拱脚处达到最大值，最大值随着滑带角度的增大而减小，并且随滑带角度越大，在相同滑坡推力作用下隧道衬砌结构上所受剪力越小，被剪切破坏的可能性减小.
2） 土压力特征
由压力盒的监测数据计算得到滑坡推力作用在隧道衬砌结构上的土压力，如表4. 可以看出：作用在隧道衬砌结构上的土压力在靠山侧大于另一侧1～2倍，拱脚处大于拱肩、拱顶处的土压力，沿着隧道衬砌结构截面分布出现出左右不均的偏压现象. 由于滑带的作用，靠山侧拱脚处土压力值最大，在滑带角度为0° 时，土压力为16.4 kPa，30° 时，土压力为9.6 kPa，50° 时，土压力为7.4 kPa，仅为滑带角度为0° 时的0.45倍，可见随着滑带角度逐渐增大，作用在拱脚处的土压力逐渐减小.
表 4 不同滑带角度下隧道土压力值Table 4. Distribution of earth pressure on tunnel under different angles of sliding zone滑带角度/（°） 土压力分布/kPa 0 
10 
20 
30 
40 
50 
3） 偏压应力比
将同样埋深情况下隧道衬砌结构左右侧洞壁上对应点的竖向应力比值定义为偏压应力比[26]. 为了全面掌握不同滑带角度作用下的偏压应力比，布置了如图3（c）所示的7个隧道衬砌结构竖向压应力分析点.
如图3（c），对于其中顶部和底部应力比，底部采用点4、5的平均值. 分别对应拱顶（点1），左右拱肩（点2、7），拱脚（点3、6）以及拱底（点4、5）. 按照拱肩（点2、7）偏压应力比Δ1，以及拱脚（点3、6）偏压应力比Δ2进行计算分析.
Δ1=σ2σ7, (1) Δ2=σ3σ6, (2) 式中：σ2、σ7和σ3、σ6分别为隧道衬砌结构监测点测得左右拱肩（点2、7）和拱脚（点3、6）应力值.
由监测元件数据换算，并根据式（1）、（2）得到表5的数值，可以得出：在拱肩位置，当滑带角度为0° 时偏压应力比为1.17，滑带角度为30° 时，偏压应力比为1.07，50° 时，偏压应力比1.01. 可见，随着滑带角度的增大，偏压应力比逐渐减小，即随着滑带角度的增大，在拱肩位置处隧道衬砌拱结构左右应力差越来越小，越来越趋于平衡拱. 在拱脚位置，当滑带角度0° 时偏压应力比为1.08，滑带角度为30°时，偏压应力比为1.29，50° 时，偏压应力比1.87. 可见，随着滑带角度的增大，偏压应力比逐渐增大，即随着滑带角度的增大，在拱脚位置处隧道衬砌拱结构左右所受应力差越来越大，趋向于偏压隧道.
表 5 模型试验下不同滑带角度隧道衬砌偏压应力比Table 5. Bias stress ratio at different sliding angles in model test滑带角度/（°） Δ1 Δ2 0 1.17 1.08 10 1.09 1.25 20 1.04 1.27 30 1.07 1.29 40 1.02 1.54 50 1.01 1.87 3. 隧道衬砌结构受力数值模拟
3.1 模型建立
根据大准铁路南坪隧道原型结构，采用有限单元法进行不同滑带角度作用下隧道衬砌结构受力分析，数值模拟中所用模型参数如表1. 模拟中设置了桩与土、隧道结构与土之间的接触单元[29-31]，材料参数中桩接触单位极限剪切力0.99 N/m，法向刚度系数0.99 kN；隧道接触单元主应力刚度模量2.45 MPa，剪切刚度模量0.245 MPa，摩擦角36°.
分别采用 0°、10°、20°、30°、40°、50°，6种滑带角度条件进行模拟分析，分析模型如图5（限于篇幅，其他未列出）.
3.2 模拟结果分析
如图6所示为 30° 滑带角度滑坡推力作用下隧道衬砌结构位移变形（其他滑带角度作用下隧道位移云图规律类似，仅位移值不同），当滑带角度为 0° 时最大变形量为121 mm，滑带角度为30° 时最大变形为59.8 mm，滑带角度为 50° 时最大变形为0.2 mm，最大变形位置均发生在靠山侧的拱脚处. 可见，随着滑带角度的增大，隧道衬砌结构变形逐渐减小，这与模型试验得出的位移规律基本一致，仅在变形量数值上略有差别.
图7为数值模拟所得隧道衬砌结构所受弯矩（其他滑带角度作用下隧道弯矩云图规律类似，仅弯矩值不同）. 与模型试验所得规律基本一致，最大弯矩值分布在靠山侧的拱脚处，当滑带角度为 0° 时最大弯矩量为487.90 kN•m，滑带角度为30° 时最大弯矩为187.00 kN•m，滑带角度为50° 时最大弯矩为89.03 kN•m. 同样地，随着滑带角度的增大，隧道衬砌结构所受弯矩逐渐减小. 在滑坡推力作用下，隧道衬砌结构拱左右受力不均，存在偏压现象.
3.3 数值模拟与模型试验对比分析
数值模拟中设置如图3的监测点，得到隧道衬砌结构上7个监测点的应力值，并根据式（1）、（2）计算出偏压应力比，如表6，与模型试验中的监测数值进行比较，数值上接近，反映出的规律一致，在拱肩位置处，随着滑带角度的增长，拱左右两侧所受竖向应力差逐渐减少，趋于平衡拱，在拱脚位置处，由于滑坡推力的作用，随着滑带角度的增大，拱左右两侧的竖向应力值越来越大，更趋于偏压隧道.
表 6 数值模拟下不同滑带角度隧道衬砌偏压应力比Table 6. Bias stress ratios in numerical simulation滑带角度/（°） Δ1 Δ2 0 1.21 0.98 10 1.20 1.22 20 1.14 1.25 30 1.11 1.48 40 1.09 1.83 50 1.06 2.34 4. 结 论
以大准铁路K20南坪隧道为例，采用室内模型试验、数值模拟手段，开展了不同滑带角度的滑坡作用下隧道衬砌结构受力特征相关研究，得到如下结论：
1） 穿越滑坡区的隧道由于滑坡推力的作用，隧道衬砌结构容易产生变形或破坏.
2） 滑坡滑带角度的不同，对隧道衬砌结构的力学作用也不同. 对于隧道衬砌结构上所受弯矩与剪应力，在靠山侧的拱脚处达到最大值，最大值随着滑带角度的增大而减小，并且随滑带角度越大，在相同滑坡推力作用下隧道衬砌结构上所受弯矩与剪应力越小. 作用在隧道衬砌结构上的土压力在靠山侧大于另一侧1～2倍，拱脚处大于拱肩、拱顶处的土压力，沿着隧道衬砌结构截面分布出现出左右不均的偏压现象，随着滑带角度逐渐增大，作用在拱脚处的土压力逐渐减小.
3） 计算得到隧道衬砌结构上不同位置处的竖向压应力，并计算出其左右两侧的偏压应力比，得出在拱肩位置，随着滑带角度的增大，隧道衬砌拱结构左右应力差越来越小，越来越趋于平衡拱. 在拱脚位置，随着滑带角度的增大，偏压应力比逐渐增大，隧道衬砌拱结构左右两侧所受应力差越来越大，趋向于偏压隧道.
在实际工程中，对于穿行大型滑坡区域的隧道，在设计过程中可在隧道衬砌结构拱脚处加强设置，同时采用抗滑桩等滑坡支挡措施抵御滑坡推力的作用.
-
图 3 道床顶面动位移空间分布
Figure 3. Spatial distribution of dynamic displacement of ballast bed surface.
图 4 路基各结构层顶面动位移沿纵向的分布
Figure 4. Longitudinal distribution of dynamic displacement along the line
图 5 不同位置各结构层动位移与荷载幅值的关系
Figure 5. Relationship between dynamic displacement at different positions and load amplitude
图 6 动位移差值与荷载幅值的关系曲线
Figure 6. Relationship between dynamic displacement difference and load amplitude
图 7 路基各结构层顶面动位移沿横向的分布
Figure 7. Lateral distribution of dynamic displacement along the line
图 8 不同位置各结构层动位移与荷载幅值的关系
Figure 8. Relationship between dynamic displacement at different positions and load amplitude
图 9 动位移差值与荷载幅值的关系曲线
Figure 9. Relationship between dynamic displacement difference and load amplitude
图 10 不同荷载工况下竖向动位移沿深度的分布
Figure 10. Distribution of dynamic displacement along depth under different load conditions
表 1 不同荷载工况下路基的动位移峰值
Table 1. Peak dynamic displacements of subgrade under different load conditions
mm 结构层 150 kN 200 kN 300 kN 400 kN 500 kN 600 kN 道床表层 1.9238 2.5702 3.8182 5.0829 6.3527 7.6513 基床表层 1.8613 2.4838 3.6894 4.9132 6.1418 7.3952 基床底层 1.8193 2.4280 3.6074 4.8030 6.0048 7.2288 路基本体 1.6660 2.2179 3.2957 4.3921 5.4917 6.6061 
下载: 导出CSV
-
国家发展改革委. 铁路“十三五”发展规划发布——铁路发展蓝图绘就[J]. 隧道建设(中英文),2017,37(12): 1584. 刘放, 张永久, 张强, 等. 战略导弹陆基多样式发射方式研究[J]. 飞航导弹, 2019（10）: 61-65 周媛. 战略导弹铁路机动发射系统的回顾与展望[J]. 中国航天,2014(11): 42-45. 周晓和,马大为,任杰,等. 某导弹无依托发射场坪动态响应与破坏形态研究[J]. 兵器材料科学与工程,2014,37(2): 77-81.ZHOU Xiaohe, MA Dawei, REN Jie, et al. Dynamic response and failure mode of a missile unsupported random launching site[J]. Ordnance Material Science and Engineering, 2014, 37(2): 77-81. MEI H, LENG W, NIE R, et al. Experimental research on the dynamic response characteristics of the transition subgrade induced by heavy-haul train passage[J]. Proceedings of the Institution of Mechanical Engineers, 2019, 233(9): 974-987. doi: 10.1177/0954409718822924 肖世伟,雷长顺. 重载铁路路基荷载特征和路基动力响应分析[J]. 铁道工程学报,2014(4): 51-56. doi: 10.3969/j.issn.1006-2106.2014.04.011XIAO Shiwei, LEI Changshun. Loading characteristics and dynamic response analysis of subgrade for heavy haul railway[J]. Journal of Railway Engineering Society, 2014(4): 51-56. doi: 10.3969/j.issn.1006-2106.2014.04.011 肖军华,郭鹏飞,周顺华,等. 既有铁路开行大轴重列车路基的动力稳定性[J]. 同济大学学报(自然科学版),2016,44(6): 884-891.XIAO Junhua, GUO Pengfei, ZHOU Shunhua. Dynamic stability of existing railway subgrade under the effect of heavy axle load trains[J]. Journal of Tongji University (Natural Science), 2016, 44(6): 884-891. 杨新文,龙天航,周顺华. 重载铁路轨道-路基系统动位移空间分布特征[J]. 同济大学学报(自然科学版),2016,44(11): 1709-1715.YANG Xinwen, LONG Tianhang, ZHOU Shunhua. Spatial distribution characteristics of displacement of heavy haul railway ballasted track-subgrade system under 30 t axle freight vehicle running[J]. Journal of Tongji University (Natural Science), 2016, 44(11): 1709-1715. GE B, WANG L, LI D. Dynamic characteristic of subgrade in da-qin heavy haul railway[J]. Revista Tecnica de la Facultad de Ingenieria Universidad del Zulia, 2016, 39(6): 146-151. SANTOS N C D, BARBOSA J, CALÇADA R, et al. Track-ground vibrations induced by railway traffic:experimental validation of a 3D numerical model[J]. Soil Dynamics and Earthquake Engineering, 2017, 97: 324-344. doi: 10.1016/j.soildyn.2017.03.004 薛富春,张建民. 移动荷载作用下高速铁路路基动应力的空间分布[J]. 铁道学报,2016,38(1): 86-91. doi: 10.3969/j.issn.1001-8360.2016.01.014XUE Fuchun, ZHANG jianmin. Spatial distribution of dynamic stresses in embankment of high-speed railway under moving loads[J]. Journal of The China Railway Society, 2016, 38(1): 86-91. doi: 10.3969/j.issn.1001-8360.2016.01.014 张瑞国. 400 km/h高速铁路与轴重40 t重载铁路基床结构设计技术探讨[D]. 成都: 西南交通大学, 2017. 邱明明,杨啸,杨果林,等. 云桂高速铁路新型全封闭路堑基床动响应特性研究[J]. 岩土力学,2016,37(2): 537-544.QIU Mingming, YANG Xiao, YANG Guolin, et al. Dynamic response of the new fully-enclosed cuttingsubgrade of Yun−Gui high-speed railway[J]. Rock and Soil Mechanics, 2016, 37(2): 537-544. 杨果林,邱明明,申权,等. 防排水结构层对铁路基床动力响应的影响研究[J]. 中国铁道科学,2016,37(2): 8-16. doi: 10.3969/j.issn.1001-4632.2016.02.02YANG Guolin, QIU Mingming, SHEN Quan, et al. Effect of waterproofing and drainage structure layer on dynamic response of railway subgrade bed[J]. China Railway Science, 2016, 37(2): 8-16. doi: 10.3969/j.issn.1001-4632.2016.02.02 肖军华,周顺华,韦凯. 列车振动荷载下铁路粉土路基的长期沉降[J]. 浙江大学学报(工学版),2010,44(10): 1912-1918.XIAO Junhua, ZHOU Shunhua, WEI Kai. Long term settlement of railroad silt subgrade induced by train loading[J]. Journal of Zhejiang University (Engineering Science), 2010, 44(10): 1912-1918. 朱剑月,练松良. 轨道结构落轴冲击动态响应有限元分析[J]. 铁道学报,2005,27(3): 76-79. doi: 10.3321/j.issn:1001-8360.2005.03.014ZHU Jianyue, LIAN Songliang. Railway track structuredynamic response under wheel load drop by use of FEM[J]. Journal of the China Railway Society, 2005, 27(3): 76-79. doi: 10.3321/j.issn:1001-8360.2005.03.014 王忆佳,曾京,高浩,等. 车轮扁疤引起的轮轨冲击分析[J]. 西南交通大学学报,2014,49(4): 700-705. doi: 10.3969/j.issn.0258-2724.2014.04.022WANG Yijia, ZENG Jing, GAO Hao, et al. Analysis of wheel/rail impact induced by wheel flats[J]. Journal of Southwest Jiaotong University, 2014, 49(4): 700-705. doi: 10.3969/j.issn.0258-2724.2014.04.022 翟婉明. 铁路轮轨冲击振动模拟与试验[J]. 计算力学学报,1999,16(1): 93-99. doi: 10.3969/j.issn.1007-4708.1999.01.014ZHAI Wanming. Simulation and experiment of railway wheel/rail impact vibrations[J]. Chinese Journal of Computational Mechanics, 1999, 16(1): 93-99. doi: 10.3969/j.issn.1007-4708.1999.01.014 张震东,马大为,胡建国,等. 弹射冲击载荷作用下沥青混凝土路面面层的损伤[J]. 工程力学,2015,32(10): 161-168. doi: 10.6052/j.issn.1000-4750.2014.02.0111ZHANG Zhendong, MA Dawei, HU Jianguo, et al. Damage of surface layer of asphalt concrete pavement under launching impact load[J]. Engineering Mechanics, 2015, 32(10): 161-168. doi: 10.6052/j.issn.1000-4750.2014.02.0111 袁成林. 强冲击作用下发射场坪动力响应研究[D]. 南京: 南京理工大学, 2018. 陈云敏,边学成. 高速铁路路基动力学研究进展[J]. 土木工程学报,2018,51(6): 1-13.CHEN Yunmin, BIAN Xuecheng. The review of high-speed railway track foundation dynamics[J]. China Civil Engineering Journal, 2018, 51(6): 1-13. 国家铁路局. 重载铁路设计规范: TB 10625—2017[S]. 北京: 中国铁道出版社, 2017. 刘晶波,杜义欣,闫秋实. 粘弹性人工边界及地震动输入在通用有限元软件中的实现[J]. 防灾减灾工程学报,2007,27(增刊): 37-42.LIU Jingbo, DU Yixin, YAN Qiushi. Application of viso-elastic artificial boundaries and seismic input in general finite element software[J]. Journal of Disaster Prevention and Mitigation Engineering, 2007, 27(S): 37-42. 刘晶波,谷音,杜义欣. 一致粘弹性人工边界及粘弹性边界单元[J]. 岩土工程学报,2006,28(9): 1070-1075. doi: 10.3321/j.issn:1000-4548.2006.09.004LIU Jingbo, GU Yin, DU Yixin. Consistent viscous-spring artificial boundaries and viscous-spring boundary element[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1070-1075. doi: 10.3321/j.issn:1000-4548.2006.09.004 杨邦强. 特种荷载作用下铁路轨道路基试验研究[D]. 成都: 西南交通大学, 2017. 易思蓉, 何华武. 铁道工程[M]. 3版. 北京: 中国铁道出版社, 2015: 246-248. 吕文强,罗强,刘钢,等. 重载铁路路基基床结构分析及设计方法[J]. 铁道学报,2016,38(4): 74-81. doi: 10.3969/j.issn.1001-8360.2016.04.011LYV Wenqiang, LUO Qiang, LIU Gang, et al. Structural analysis and design method for subgrade bed of heavy haul railway[J]. Journal of the China Railway Society, 2016, 38(4): 74-81. doi: 10.3969/j.issn.1001-8360.2016.04.011 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 586
- HTML全文浏览量: 252
- PDF下载量: 20
- 被引次数: 0