Dynamic Response Characteristics of Bridge-Tunnel Transition Section with Deep Buried Pile-Plank Structures
-
摘要:
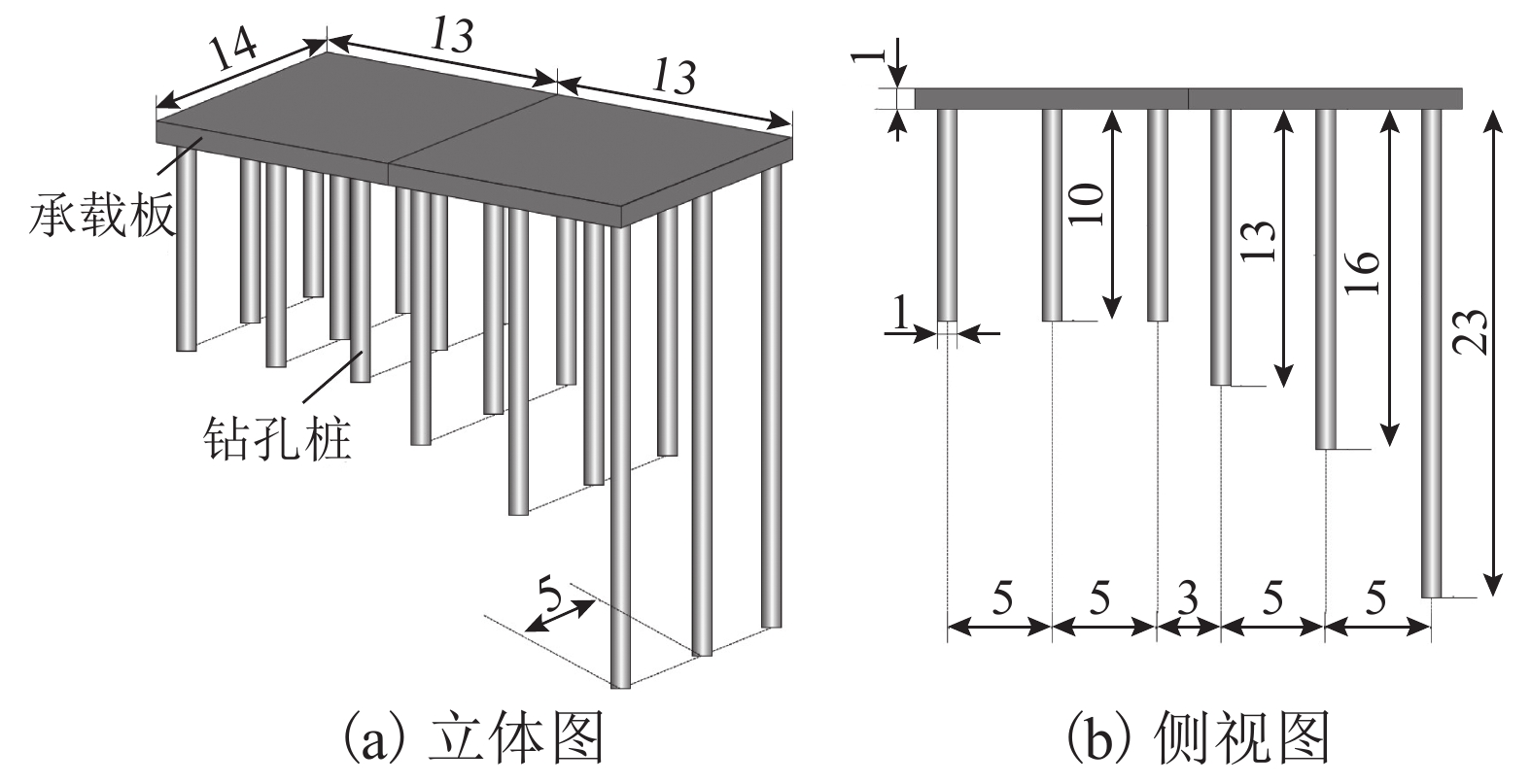
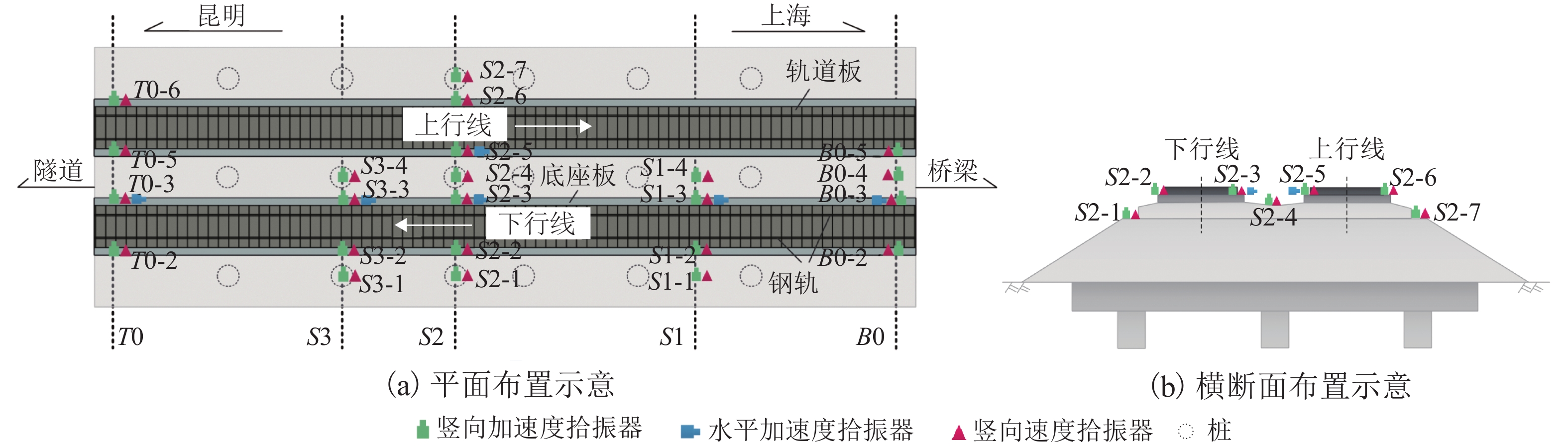
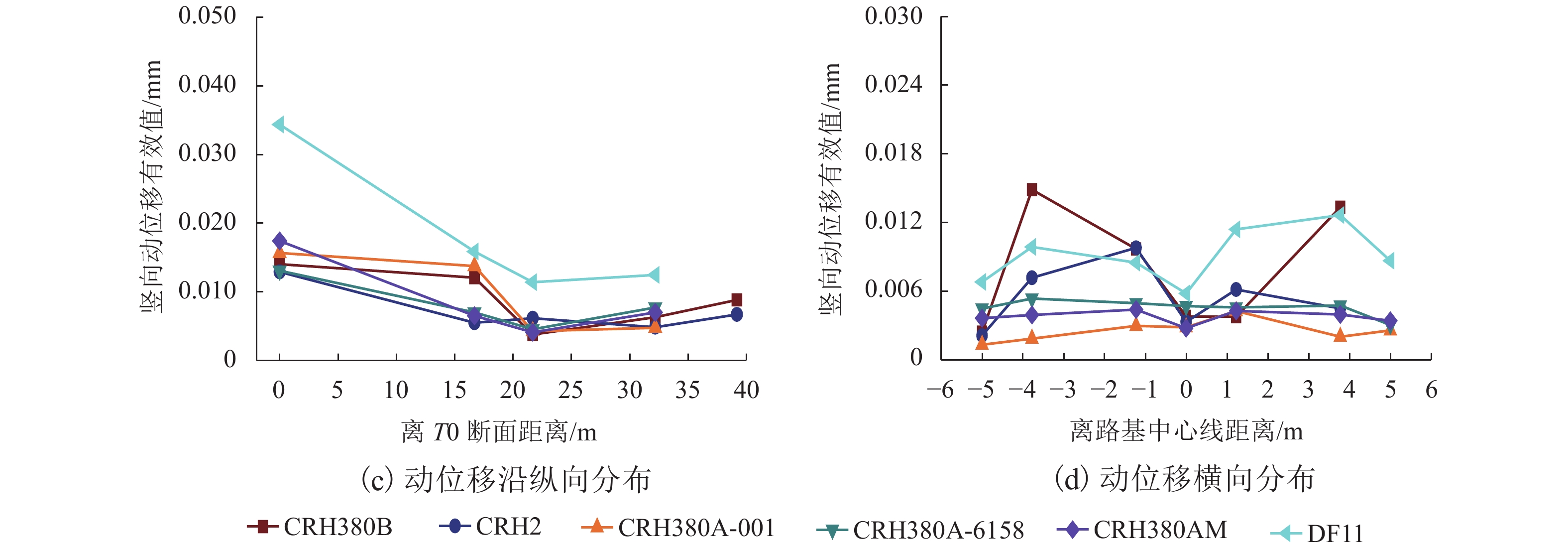
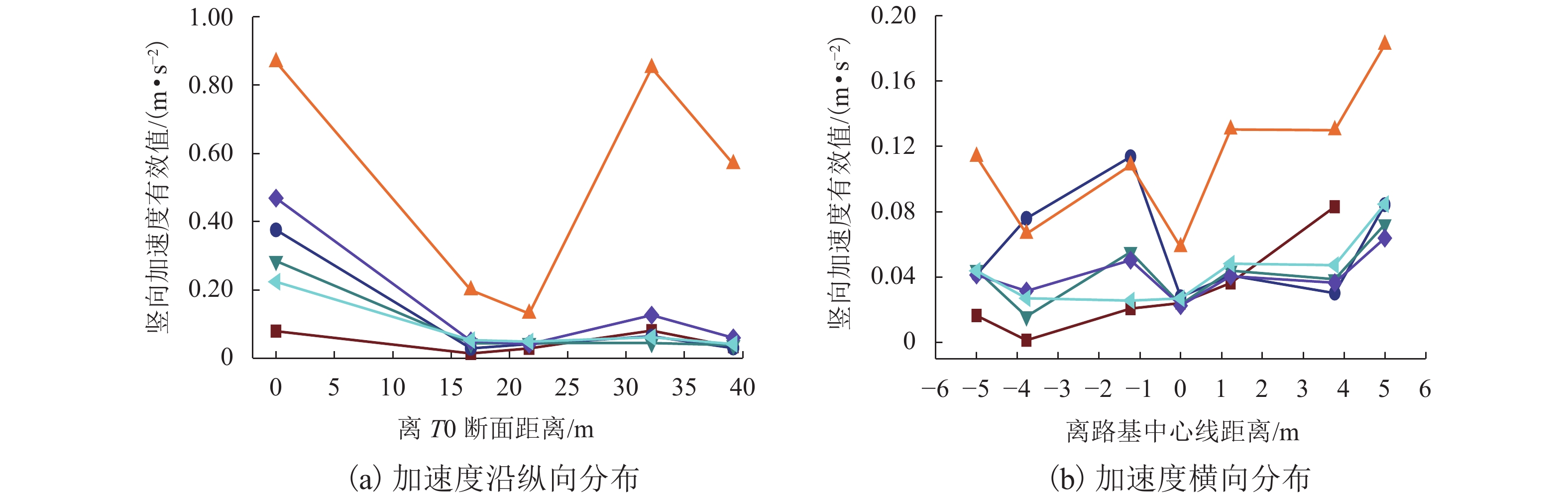
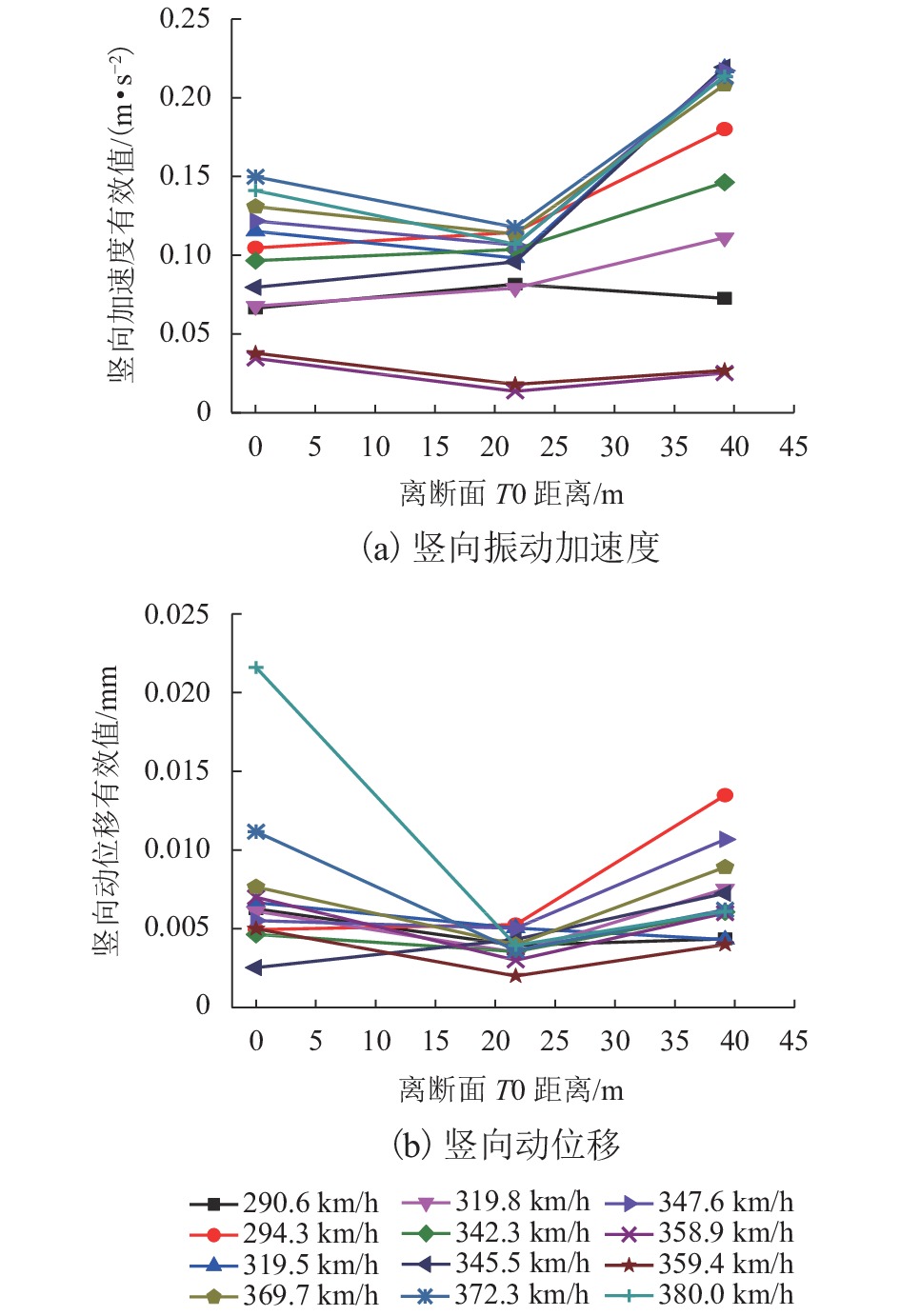
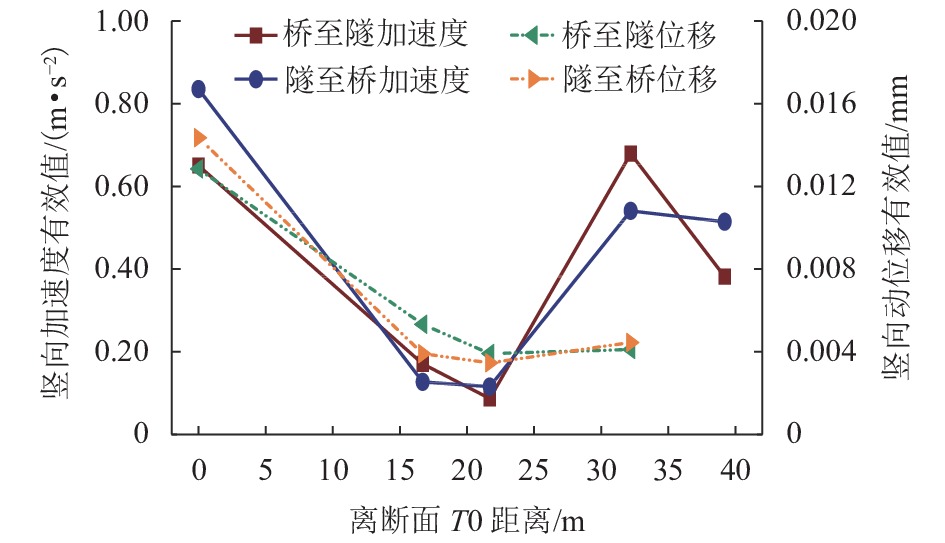
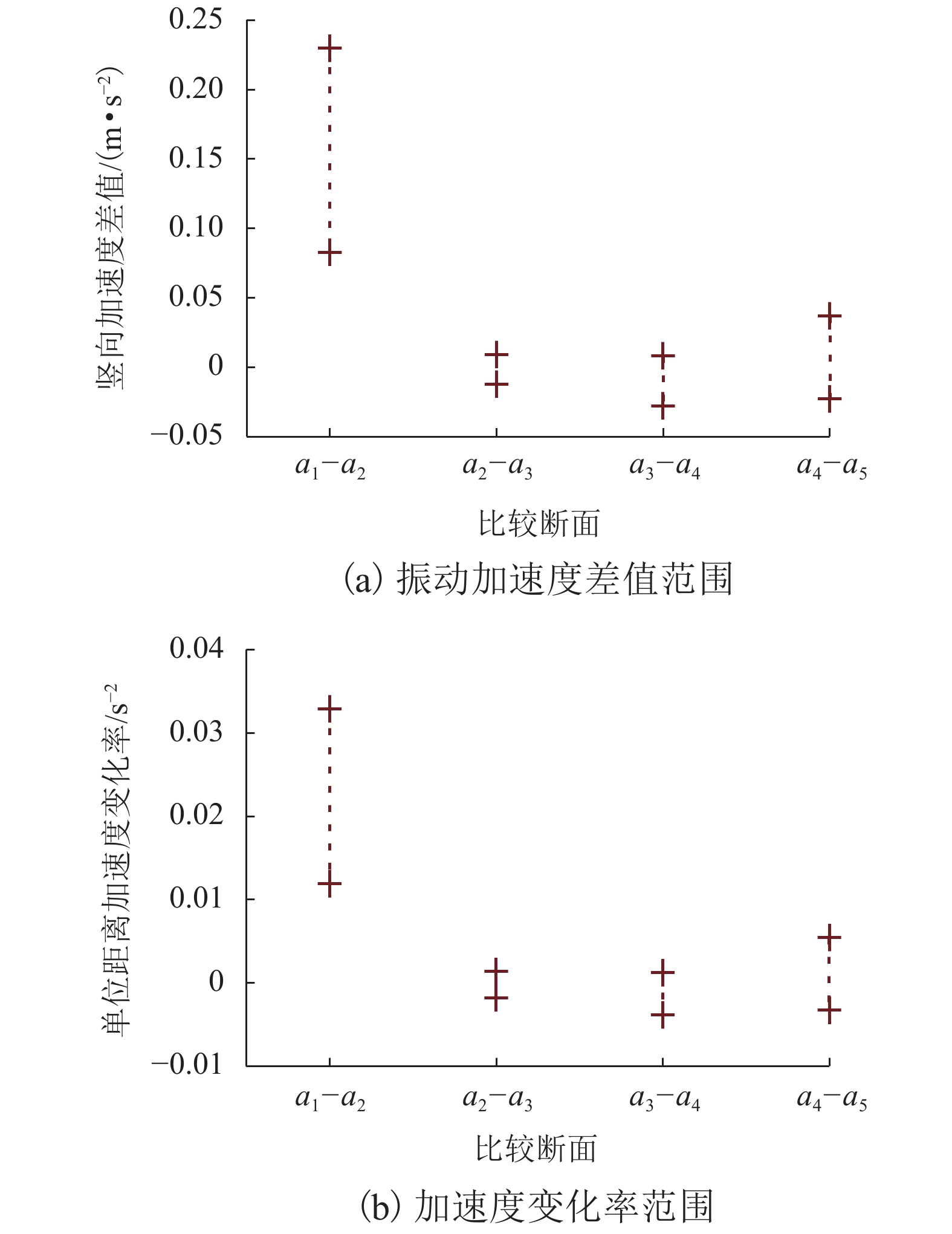
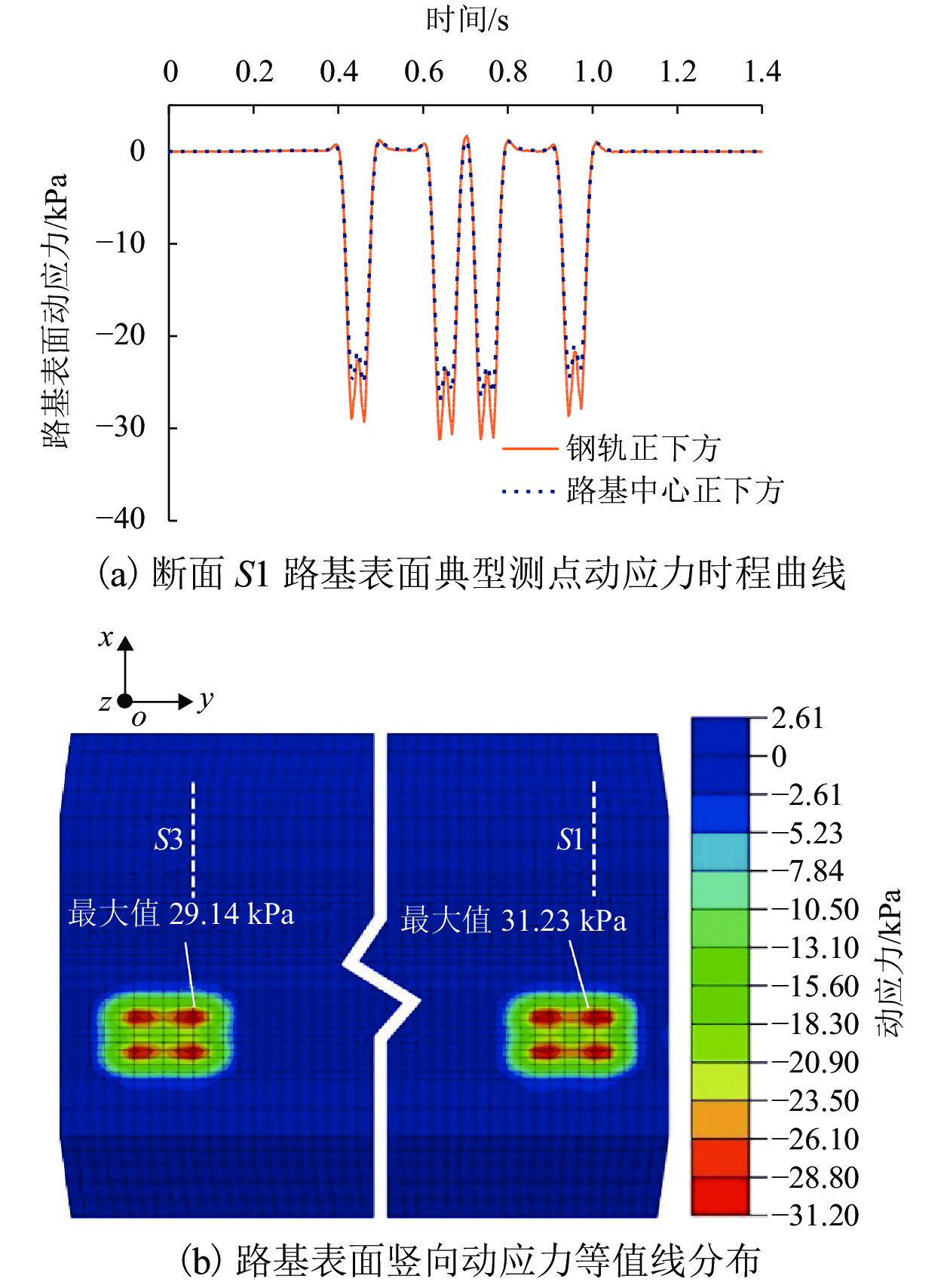
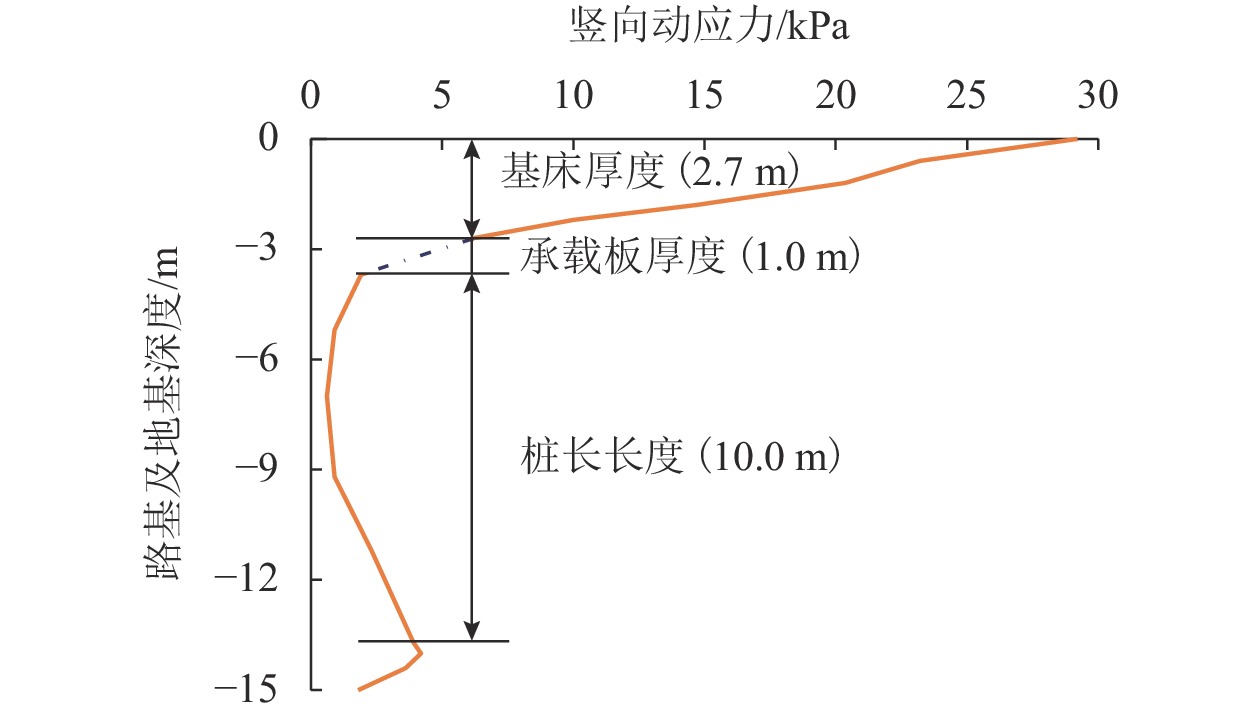
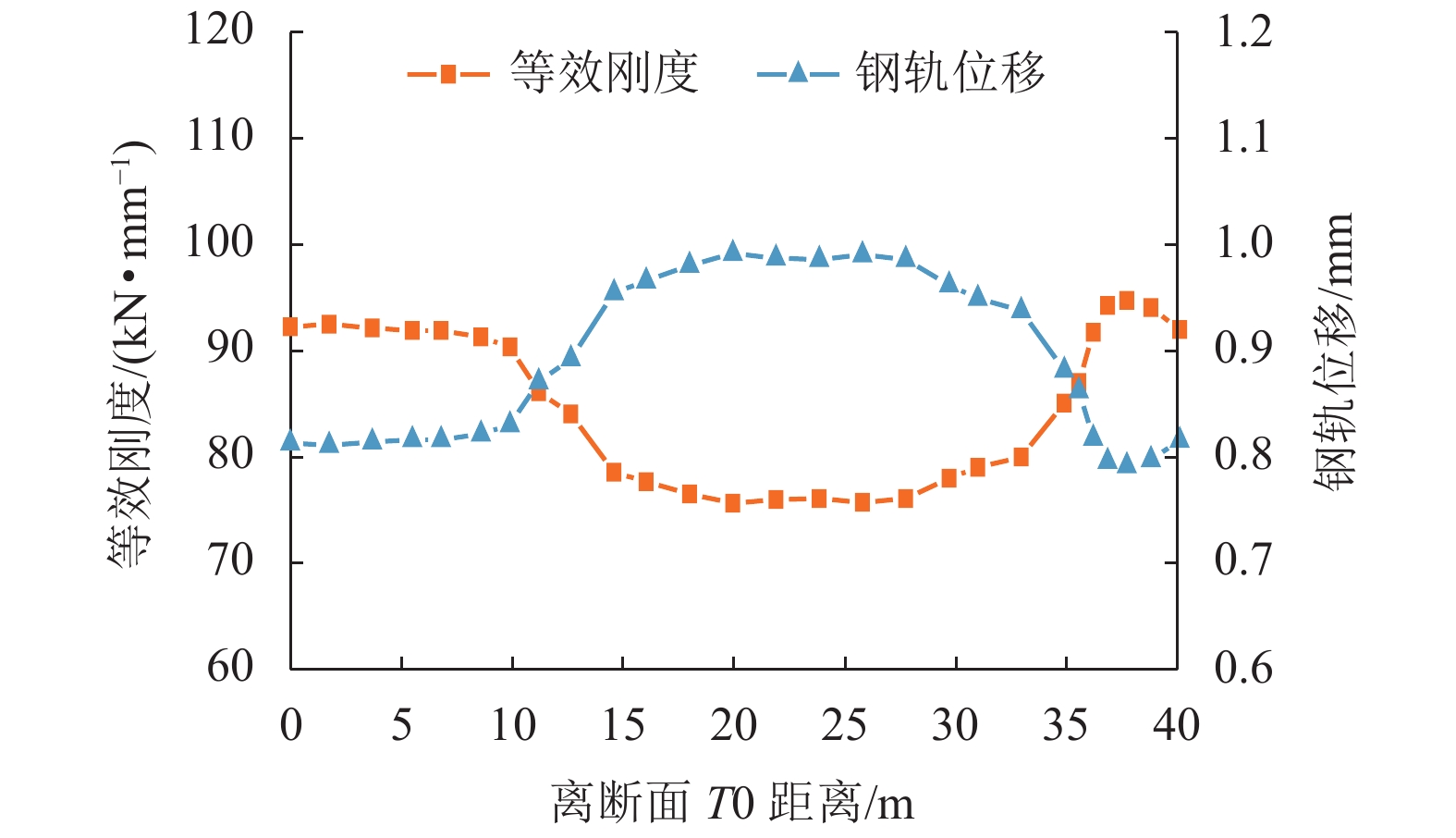
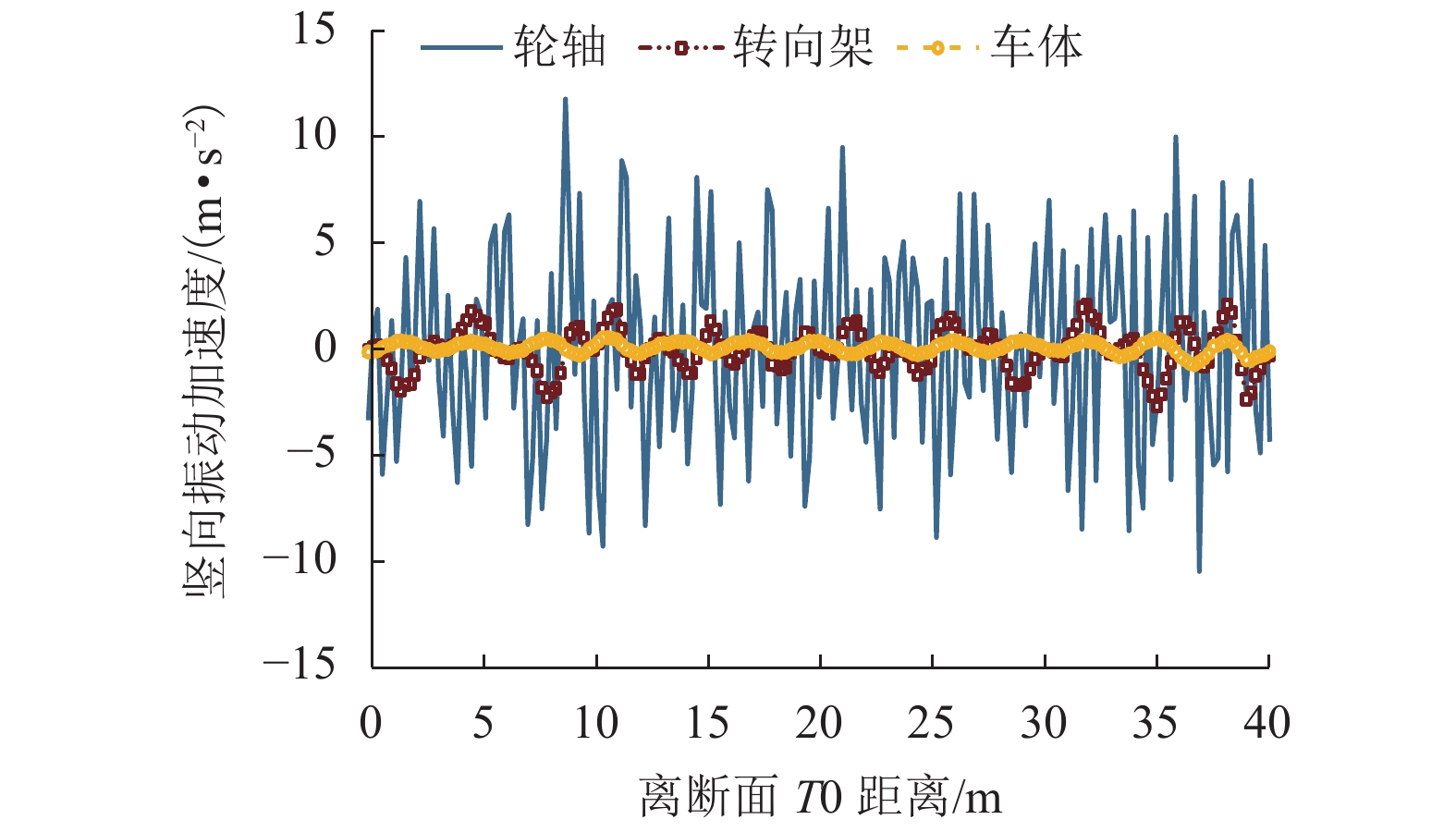
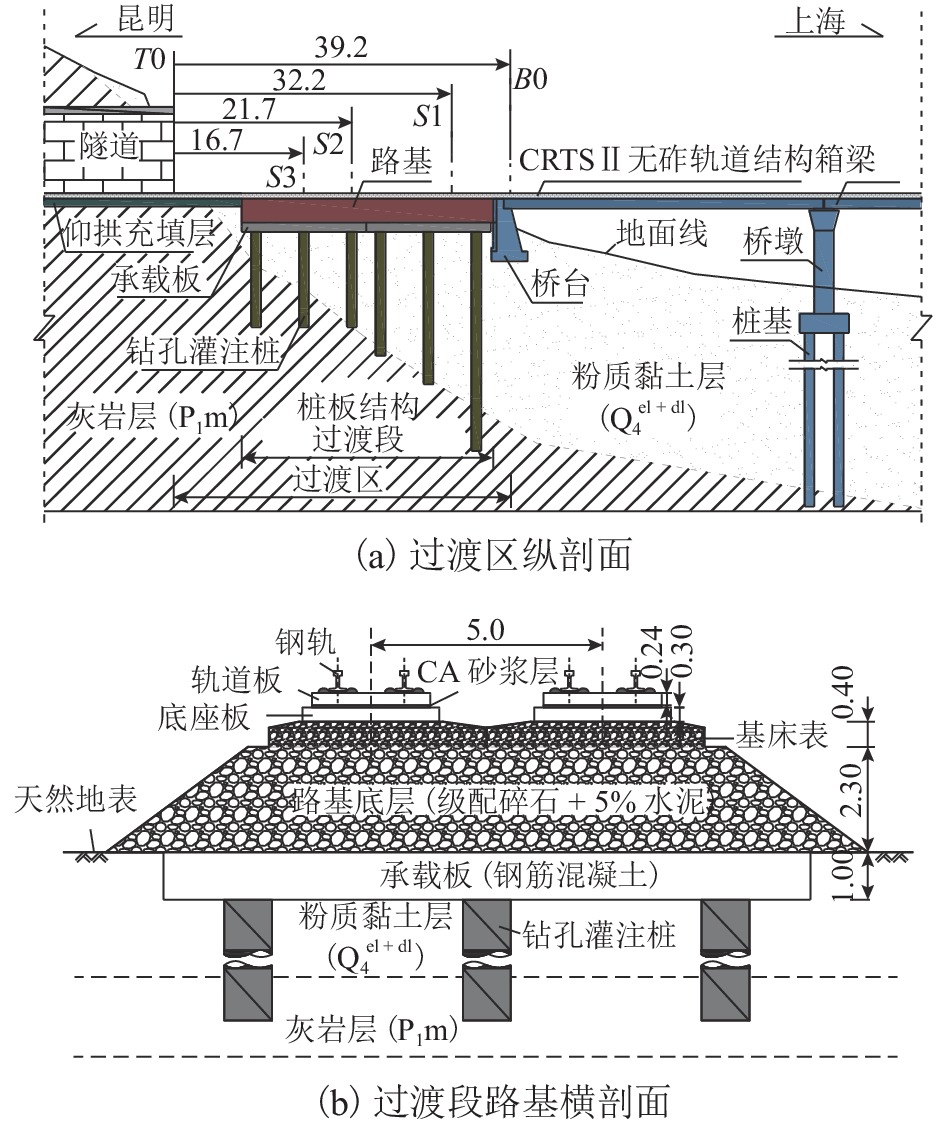
为了解深埋式桩板结构桥-隧过渡段的动力特性及过渡性能，在沪昆高铁某工点过渡区（含隧道口、过渡段及桥台）开展现场动力响应测试，分析不同车型、车速及行车方向等工况下过渡区的动力响应分布规律；并建立考虑车辆-轨道-路基耦合振动数值模型，研究过渡区的线路平顺性及桩板结构过渡段的动应力分布. 研究结果表明：不同车型列车激励下，过渡区振动加速度及动位移有效值的最大值分别为0.85 m/s2、0.034 mm，过渡段的振动水平要比隧道及桥台的更低；过渡段动力响应有效值随车速增大而增大，其增幅比隧道与桥台的更小；行车方向对过渡段与桥台连接区域的动力响应影响较大，对其他断面影响微弱；列车以300 km/h车速经过该过渡区时，过渡区钢轨挠度最大变化率约为0.149 mm/m，车体竖向加速度最大值为0.74 m/s2；桩板结构的存在能够将列车荷载传递至深部地基，使浅层地基土体承受的动力作用降低.
Abstract:To understand the dynamic characteristics and performances of bridge-tunnel transition sections with deep buried pile-plank structures (DBPPS), dynamic field tests were performed on a transition zone including a tunnel entrance, a transition section and a abutment in the Shanghai—Kunming high-speed railway to investigate its dynamic response distributions under running trains with different train types, speeds and driving directions. A numerical model considering vehicle-track-subgrade coupled interaction was then established to study the railway line smoothness along the transition zone and the vertical dynamic stress distribution of the DBPPS subgrade. Results show that under the train loads with different train types, the maximum effective values of acceleration and displacement along the transition zone are 0.85 m/s2 and 0.034 mm, respectively. The vibration level of the transition section is lower than that of the tunnel and the abutment. The effective values of dynamic response in the transition section increase with the increasing train speed, and its increase rate is smaller than that of the tunnel and the abutment. The driving directions have a significant influence on the dynamic responses in the connection between the transition section and the abutment, but have a weak influence on other sections. When the train passes through the transition zone at a speed of 300 km/h, the maximum change rate of rail deflection is approximately 0.149 mm/m, and the maximum vertical acceleration of the carbody is 0.74 m/s2. The pile-plank structure can transfer the train load to the deep foundation and reduce the dynamic effect on shallow soil of the foundation.
-
随着无人驾驶技术的发展，未来道路上的智能网联车（connected automated vehicle，CAV）将逐渐普及. 但最新研究表明[1]，预计2045年道路上L4级别的CAV渗透率仅能达到24.8%. 因此，未来很长一段时间内，道路上将普遍呈现由常规车（regular vehicle，RV）、网联人工驾驶车（connected vehicle，CV）和CAV组成的混合交通流. 网联车（CV和CAV）能够提供海量的车辆轨迹数据，而这些数据蕴含了丰富的时空交通信息，是交通状态估计的基础数据之一. 但由于RV无法提供自身的轨迹数据，在智能网联环境下全样本车辆轨迹数据仍难以获得. 因此，如何利用已有的轨迹数据来重构所有车辆的轨迹具有重要的意义[2].
近年来，有许多学者对车辆轨迹重构问题进行了探讨，主要为基于经典交通流理论和基于统计概率模型的方法. 这些方法按轨迹重构数据来源可分为三大类：定点检测器、移动检测器和多源数据. Coifman[3]基于双线圈检测器数据和交通流理论，通过在时空图中估计路段行程时间重构车辆轨迹. Rao等[4]利用车牌识别数据构建了一种车辆路径重构方法，进一步可基于路径对交通网络的历史OD （original-destination）进行估计. Hao等[5]、Wan等[6]、Shan等[7]基于概率论的思想，分别采用随机模型、期望最大化算法（expectation-maximum，EM）及最大似然估计，从微观角度重构浮动车任意相邻采样点之间的运动轨迹. Li等[8]提出了基于K最近邻回归算法利用不完整轨迹来扩充轨迹样本量. Xie等[9]基于修正的交通信号配时方案、车辆通过时间和车辆行程时间构建微观仿真环境，实现了对干道车辆轨迹重构. Mehran等[10]通过融合秒级浮动车数据、音视频数据（audio video interleaved，AVI）及信号控制参数，提出了一种基于变分理论城市干道车辆运行轨迹估计方法，并利用东京一条包含五个交叉口的单行道实测数据进行了方法验证和误差分析. 唐克双等[11]通过融合视频和定点检测器流量数据，基于交通流理论和交通仿真思想，构建了一种不依赖高频浮动车数据，适用于多车道的轨迹重构方法. 综上分析可知，现有研究均能够对车辆轨迹数据进行有效重构，但均只考虑了人工驾驶环境，未考虑未来智能网联混合交通流的情况. 随着智能网联技术的发展，CAV除了能提供自身轨迹数据外，还能通过感知设备（摄像头和雷达）提供自身一定范围内的车辆轨迹数据. 因此，CAV采集的移动传感数据将会给轨迹重构提供一种新的思路. 如何充分考虑混合交通流环境下不同车辆类型提供的数据，构建全样本车辆轨迹重构模型，是未来CAV环境下车辆轨迹重构亟待解决的关键问题.
为解决该问题，本文拟研究混有RV、CV和CAV的混合交通流全样本车辆轨迹重构方法. 充分利用CAV和CV提供的轨迹数据信息，提出基于跟驰特性的混合交通流轨迹重构模型，并通过仿真试验验证模型在不同交通流密度和CAV渗透率条件下的合理性与有效性.
1. 跟驰特性分析
在本文研究中，不考虑车辆换道的影响，选取较为简单的场景来阐述轨迹重构思想. 在微观交通流分析中，一般采用跟驰模型描述车辆之间的跟驰行为. 该模型认为当前车辆是否加减速与本身速度、前后车速度差和位置差有关. 因此，在已知部分轨迹的情况下，采用该模型可分析相邻轨迹中存在其他车辆轨迹的可能性.
跟驰模型主要可分为五种类型：刺激反应模型、安全间距模型、社会力模型、优化速度模型和低阶线性模型[12]，均可作为本文轨迹重构的基础模型. 而作为社会力模型的一种，智能驾驶员模型（intelligent driver model，IDM）能够很好地描述熟练驾驶员的驾驶习惯，应用范围更广. 因此，本文以IDM为例描述车辆之间的跟驰特性，如式（1）所示.
ap(t)=aM[1−(vp(t)vf)δ−(s0+Tvp(t)+vp(t)[vp(t)−vp−1(t)]2√aMbxp−1(t)−xp(t))2], (1) 式中：ap(t)为时刻t车辆p的加速度；vf为期望速度；aM为最大加速度；T为安全车头时距；b为舒适减速度的绝对值；s0为最小停车间距；vp(t)为时刻t车辆p的速度；xp(t)为时刻t车辆p的位置；δ为加速度指数（一般取4）.
2. 基于IDM的车辆状态估计
2.1 数据环境分析
本文研究的混合交通流中有三种类型的车辆：RV、CV和CAV. 其中，CAV除提供自身的轨迹数据外，还可通过感知设备获取周围一定范围内的车辆位置和状态信息，因此，能提供周围一定范围内车辆的轨迹数据. 混合交通流中不同车辆组成如图1所示. CAV探测范围内的车辆信息均可采集，不论是RV还是CV. CV由于不具备感知设备，所以只能提供自身的轨迹数据. 而RV由于其不具备或未打开联网功能，所以既不能提供自身的轨迹数据，也不能提供周围车辆的轨迹数据.
图 1 混合交通流中不同车辆组成Figure 1. Composition of different types of vehicles in mixed traffic flow从以上分析可知，在该混合交通流环境下，主要需要对CAV探测范围之外的RV进行轨迹重构. 混合交通流轨迹时空图如图2所示. CAV两辆（CAV1、CAV2），CV三辆（CV1、CV2、CV3）；将阴影区域A中前一辆CAV探测到的最后一辆车记为Vn−1，后面一辆CV记为Vn；红色虚线表示CAV轨迹；蓝色点线表示CV轨迹；黑色实线表示RV轨迹；阴影区域A和B即为需要重构轨迹的区域. 在跟驰模型中，本车的跟驰行为主要与前车有关，即前车的轨迹直接影响本车的轨迹. 以阴影区域A为例，若区域A中无其他车辆，Vn会跟随Vn−1，本车Vn与前车Vn−1构成跟驰行为，可采用跟驰模型进行描述. 但若区域A中还存在未被观测的RV，则本车Vn用跟驰模型计算的加速度会与实际加速度存在较大差异. 因此，构建轨迹重构模型试图寻找区域A内的最佳轨迹条数，来实现这种差异的最小化.
CV提供的轨迹数据可分为是否在CAV的检测范围内. 当CV在CAV的检测范围内，如图2中的CV1和CV3，这两辆车的轨迹可直接由CAV观测，故该车提供的数据有无对整个模型的求解没有影响. 当CV不在CAV检测范围内时，如图2中的CV2，此时需要利用该轨迹和CAV提供的轨迹重构阴影区域A和B中的车辆轨迹.
2.2 估计插入车辆的速度
车辆时空轨迹示意如图3所示，图中：A1,A2,⋯,Ak为时空区域；k为时间总步数；Δt为时间步长；xn(Δt)为Δt时Vn的位置. 考虑到交通流稳定时，前后车的速度差别较小. 因此，第k个时空区域Ak中车辆Vn的速度vn的估计如式（2）所示[13].
vn=d(Ak)T(Ak)=xn−1(t+Δt)−xn−1(t)+xn(t+Δt)−xn(t)2Δt, (2) 式中：d(Ak)和T(Ak)分别为区域Ak的位置差和时间差.
由于插入的RV在区域 Ak中，因此，该车在时刻 kΔt的速度可以用区域 Ak的速度 v(Ak)进行估计.
2.3 估计插入车辆的位置
在任意时刻，插入车辆的位置都需满足与前后车之间的安全间距. 因此，将Vn前插入的第i辆车记为Vn,i，Vn,i的位置xn，i只能出现在一定的区间范围内，如式（3）所示.
xn(t)+s0+l⩽xn,i(t)⩽xn−1(t)−s0−l, (3) 式中：l为车身长度.
当获得插入车辆的速度和可能位置区间后，可将Vn,i和Vn分别作为前车和后车，而Vn,i插入位置xn,i(t) 会对后车Vn产生影响，这种影响会反映到后车的加速度上. 因此，可以根据IDM代入式（1）计算Vn的加速度 ˆan(xn,i(t)).
当 xn,i(t) 在可行域内取不同的值时，Vn会得到不同的加速度. 而当估计加速度 ˆan(xn,i(t))与实际加速度 an(t) 最接近时，对应的 xn,i(t) 即为要插入车辆Vn,i的位置.
因此，可构建目标函数求得最优的插入车辆位置，同时考虑到车辆不同时刻的位置即为车辆的轨迹，可选用Vn的实际加速度和估计加速度之间均方根误差最小为优化目标，如式（4）所示.
min (4) 综上，该优化模型的目标函数为式（4），约束条件为{{x_{n,i}}} 和{{\hat a}_n}( {{x{_{n,i}(t)}}})，为典型的非线性优化模型，可用MATLAB自带的函数直接进行求解.
3. 基于IDM的车辆轨迹重构
由第2节的分析可知，得出插入车辆后，可由模型计算其插入的位置和速度. 因此，车辆轨迹重构模型即为需要寻找已知轨迹中间未知轨迹的数量，插入车辆轨迹示意如图4所示. 当插入车辆数已知时，可采用第2节中的方法依次求得每辆插入车辆轨迹的具体位置和速度. 考虑到车辆之间的最小安全间距，插入车辆数m的最大可能取值为N，如式（5）所示.
\begin{split} & N = {\rm{ent}}\left( {\rm{min}} \left\{ {\dfrac{{{x_{n - 1}}\left( 0 \right) - {x_n}\left( 0 \right)}}{{{s_0} + l}},\dfrac{{x_{n - 1}}\left( {\Delta t} \right) - {x_n}\left( {\Delta t} \right)}{{{s_0} + l}},}\cdots, \right. \right. \\ &\quad \left. \left. { \dfrac{{{x_{n - 1}}\left( {k\Delta t} \right) - {x_n}\left( {k\Delta t} \right)}}{{{s_0} + l}}}\right\}\right) . \\[-20pt] \end{split} (5) 在车辆{{\rm{V}}_n}和车辆{{\rm{V}}_{n - 1}}之间依次插入的m辆车({{\rm{V}}_{n,1}},{{\rm{V}}_{n,2}},\cdots,{{\rm{V}}}_{n,m}）， {{\rm{V}}_{n,m}}为距离{{\rm{V}}_n}最近的车辆，即为{{\rm{V}}_n}的前车. 插入m辆车后，类比式（2），可粗略估计{{\rm{V}}_{n,m}}的速度和位置分别如式（6）、（7）所示.
{v_{n,m}}\left( t \right) = {v_n}\left( t \right) - \frac{{ {{v_n}\left( t \right) - {v_{n - 1}}\left( t \right)} }}{{ {m + 1} }}, (6) {x_{n,m}}\left( t \right) = {x_n}\left( t \right) - \frac{{{{x_n}\left( t \right) - {x_{n - 1}}\left( t \right)} }}{{{m + 1} }}. (7) 在估计插入的速度和位置后，可重构{{\rm{V}}_{n,m}}的轨迹. 根据IDM由{{\rm{V}}_{n,m}}的轨迹可求出{{\rm{V}}_n}的加速度. 插入m辆RV后代入式（1）可计算{{\rm{V}}_n}的理论加速度.
此处，选用{{\rm{V}}_n}加速度的均方根误差作为衡量标准，则均方根误差最小时对应的m即为最佳插入的车辆数，如式（8）所示.
\mathop {{\rm{arg min}}}\limits_m \sqrt {\frac{1}{k}{{\sum\limits_{t = 0}^{k\Delta t} {\left[ {{{\hat a}_n}\left( {{x_{n,i}}(t)} \right) - {a_n}\left( t \right)} \right]^2} }}}. (8) 因此，该问题也为一个非线性优化问题，目标函数为式（8），约束条件为式（1）、（6）、（7）. 综上，当确定最佳插入车辆数量以后，可采用第2节中的方法对每一插入车辆轨迹进行精确地重构.
4. 数值仿真分析
4.1 仿真参数设置
为验证模型的有效性，基于IDM设计元胞自动机进化规则，模拟单车道高速公路交通流运行规律. 所有车辆之间跟驰行为均用IDM描述[14-15]. 仿真路段长度1000 m，元胞长度0.1 m，仿真时间1000 s，仿真步长1 s. 为使仿真数据更趋向于真实数据，在仿真过程给车辆设置随机减速模拟真实道路上的车流运行状况.
本文共设计两种基准试验方案，第一种方案是将CAV的渗透率恒定为8%，CV渗透率恒定为20%，改变试验中的交通流密度，研究不同交通流密度对模型的影响. 第二种方案将交通流密度设定为70 辆/km，改变CAV和CV的渗透率，研究不同渗透率对模型的影响. 本文IDM的参数[16]取值为：{s_0}=2 m，{a_{\rm{M}}}=1 m/s2，T=1.5 s，b=2 m/s2，l=4.5 m.
4.2 交通流密度的影响
为研究道路上交通流密度对本文模型结果的影响，将CAV和CV的渗透率分别设定为8%和20%. 首先，可基于仿真试验获取路段的流量-密度-速度关系如图5所示.
图 5 流量-密度-速度关系Figure 5. Relationship between volume，density and speed of traffic flow由图5可知：仿真路段中的最佳密度为40 辆/km，即当交通流密度大于40 辆/km时，路段上的车辆开始出现拥挤；当交通流密度大于70 辆/km时，车辆的平均速度低于20 km/h，而高速公路中很少出现车辆速度小于20 km/h的情况. 因此，为研究本文模型在不同交通状态下的重构效果，此处将交通流密度设为20、30、40、50、60、70 辆/km. 为避免随机因素的影响，同一交通流密度下采用不同的随机种子进行仿真和轨迹重构，取其平均值作为最终结果. 轨迹重构图像示例如图6所示. 不同交通流密度条件下求得的插入车辆数如表1所示.
图 6 交通流密度为60辆/km时轨迹时空图Figure 6. Spatio-temporal diagram of the trajectories when traffic flow density is 60 veh/km由表1可知：当交通流密度小于等于40 辆/km时，会出现插入的车辆数小于实际车辆数；而当交通流密度大于40 辆/km时，则出现插入的车辆数大于实际车辆数. 从百分比误差来看，当出现拥堵前，随着交通流密度的增加，模型求得的插入车辆数的误差逐渐减小，插入辆数的百分比误差也逐渐减小；当出现拥堵后，随着交通流密度的增加，模型求得的插入车辆数的误差逐渐增加，插入辆数的百分比误差也逐渐增大. 分析可知，开始拥堵之前，大多数车辆自由行驶，且车辆之间相互干扰较少，所以误差较大. 开始拥堵后，当两辆车之间插入的车辆数较大时，模型求得的插入车辆数会产生一定的误差. 随着交通流密度的增大，车辆之间的间距逐渐减小，出现两辆车之间插入的车辆数较大的情况增多，故插入辆数的误差逐渐增大.
表 1 不同交通流密度条件下插入车辆数估计Table 1. Estimation of the numbers of inserted vehicles under different traffic densities交通流密度/
（辆•km−1）CAV/
辆插入车辆/辆 实际车辆/辆 插入误差/辆 插入误差百分比/% 20 2 5.80 6.40 0.60 9.38 30 2 14.05 13.80 0.35 2.54 40 3 15.80 16.05 0.25 1.56 50 4 21.75 21.38 0.31 1.50 60 5 27.85 25.75 2.10 8.16 70 6 31.40 27.25 4.30 15.78 注：表中插入车辆数为多次仿真试验的平均值，因此会出现不是整数的情况；插入误差百分比为插入辆数的误差与实际插入车辆数的百分比. 当交通流密度小于60 辆/km时，本文模型求得的插入车辆数的误差小于1辆，误差小于10%. 综上分析可知，本文模型求得的插入车辆数较为准确，适用于高速公路的各种交通状态.
为进一步评估本文模型的轨迹插入效果，选用每一时刻插入车辆的实际和估计位置之间的平均绝对误差（MAE，eMAE）、平均绝对百分比误差（MAPE，eMAE）和均方根误差（RMSE，eMAE）表征重构轨迹的准确性，分别如式（9）～（11）所示.
{e_{\rm{MAE}}} = \frac{1}{k}\sum\limits_{t = 0}^{k\vartriangle t} {\left| {\hat x(t) - x(t)} \right|}, (9) {e_{\rm{MAPE}}} = \frac{1}{k}\sum\limits_{t = 0}^{k\Delta t} {\left| {\frac{{\hat x(t) - x(t)}}{{x(t)}}} \right|}\; \times \; {100{\text{%}} }, (10) {e_{\rm{RMSE}}} = \sqrt {\frac{1}{k}\sum\limits_{t = 0}^{k\Delta t} {{{\left[ {\hat x(t) - x(t)} \right]}^2}} }, (11) 式中：\hat x(t)为插入车辆的估计位置；x(t)为插入车辆的实际位置.
根据式（9）～（11），可得不同交通流密度下的误差值，如表2所示. 由表2可知：当交通流密度为20 辆/km时，由于需要插入的车辆数过少，所以重构轨迹车辆位置的平均绝对误差相较其他密度较高. 当交通流密度大于20 辆/km时，重构轨迹车辆位置的误差随着交通流密度的增大而增加，但变动幅度不大. 在不同的交通流密度条件下，重构轨迹车辆位置的平均绝对误差的平均值为12.97 m，平均绝对百分比误差的平均值为0.37%，均方根误差的平均值为19.55 m. 从整体上来说，本文模型在不同交通流密度下重构轨迹车辆位置的误差较为稳定.
表 2 不同交通流密度条件下轨迹重构误差Table 2. Trajectory reconstruction error under different traffic density conditions交通流密度/
（辆•km−1）CAV/
辆MAE/
mMAPE/
%RMSE/
m20 2 15.02 0.36 18.28 30 2 11.90 0.29 14.30 40 3 12.14 0.31 18.68 50 4 12.30 0.35 20.39 60 5 13.09 0.42 22.19 70 6 13.39 0.52 23.47 平均值 12.97 0.37 19.55 4.3 CAV和CV渗透率的影响
CAV和CV提供的数据作为模型的已知数据，研究其渗透率对模型结果的影响尤为重要.
4.3.1 CAV渗透率的影响
为研究不同CAV渗透率对模型结果的影响，将交通流密度设为70 辆/km，CV渗透率设为20%. CAV的检测范围设为100 m. 若车辆在道路上均匀分布，则CAV检测范围包含7辆车. 但考虑到车辆的随机分布和感知设备的误差，此处假设CAV能记录检测范围内车辆数为6. 将CAV渗透率分别设置为4%、6%、8%、10%、12%和14%，研究不同渗透率下的车辆轨迹重构效果，其中，插入车辆数估计误差如表3所示，轨迹重构结果示例如图7所示.
表 3 不同渗透率条件下插入车辆数估计Table 3. Estimation of the numbers of inserted vehicles under different CAV penetration ratesCAV
渗透率/%CAV/辆 插入
车辆/辆实际
车辆/辆插入
误差/辆插入误差
百分比/%4 3 45.50 38.70 6.80 17.57 6 4 41.50 35.20 5.80 16.48 8 6 31.40 27.25 4.30 15.78 10 7 29.44 25.44 4.00 15.72 12 8 26.80 23.20 3.60 15.52 14 10 19.60 17.00 2.60 15.29 
图 7 CAV渗透率为14%时轨迹时空图Figure 7. Spatio-temporal diagram of the trajectories when CAV penetration rate is 14%由表3可知：当道路上的交通流密度为70 辆/km时，随着CAV渗透率的增加，需要插入的车辆数减少，轨迹重构的难度减小，求出的插入车辆数的误差和百分比误差均逐渐减小；当渗透率只有4%的情况下，模型也能够较好地估计插入轨迹的数量. 因此，本文模型在未来不同渗透率环境下均能很好应用. 进一步，可计算重构轨迹车辆位置误差如表4所示.
表 4 CAV不同渗透率条件下轨迹重构误差Table 4. Trajectory reconstruction error under different CAV penetration ratesCAV渗
透率/%CAV/辆 MAE/m MAPE/% RMSE/m 4 3 16.76 0.68 33.77 6 4 15.69 0.63 28.95 8 6 13.39 0.52 23.47 10 7 12.98 0.51 21.86 12 8 12.23 0.49 19.90 14 10 10.45 0.42 16.45 由表4可知：当道路上的交通流密度为70 辆/km时，随着CAV渗透率的增加，重构轨迹车辆位置的误差逐渐减小，即本文模型的准确性逐渐提高. 以MAE为例，当CAV的渗透率在4%～8%范围内时，平均每增加一辆CAV，平均绝对误差减小1.12 m. 当CAV的渗透率在8%～14%范围内时，平均每增加一辆CAV，平均绝对误差减小0.73 m. 因此，当CAV渗透率大于8%时，平均绝对误差趋于稳定.
4.3.2 CV渗透率的影响
将交通流密度设为70 辆/km，CAV渗透率设为8%，研究CV渗透率为16%、18%、20%、22%、24%时轨迹重构结果，如表5所示.
表 5 CV不同渗透率轨迹重构结果Table 5. Reconstruction results of different CV penetration ratesCV 渗透率/% CV/辆 插入
误差/辆插入误差
百分比/%MAE/m MAPE/
%RMSE/
m16 11 5.40 0.18 17.46 0.69 32.43 18 13 4.33 0.16 13.98 0.55 24.27 20 14 4.30 0.16 13.39 0.52 23.47 22 15 4.20 0.15 12.93 0.52 21.50 24 17 3.80 0.14 11.50 0.48 19.11 由表5可知：随着CV渗透率的提高，插入辆数的误差逐渐减小，插入数量的百分比误差也逐渐减小，即轨迹重构效果不断提升. 此外，车辆位置的误差也越小，即轨迹重构的准确性有所提高.
为研究CAV和CV渗透率对试验结果的影响，以CAV渗透率为横轴，CV渗透率为纵轴，绘制均方根误差热力图，如图8所示.
由图8可知：均方根误差趋势为随着CAV或CV渗透率的提高，轨迹重构效果逐渐变好. 但与CV渗透率相比，CAV渗透率对结果的影响更大. 分析可知，增加一辆CAV能够获得道路上多辆车的轨迹数据，而增加一辆CV，只能获取该车的轨迹数据. 因此，当CAV渗透率较高时，已知轨迹的车辆较多，此时CV对试验结果的影响较小.
5. 结 论
1） 在出现拥堵前，随着交通流密度的增加，本文模型求得的插入车辆数的误差逐渐减小；而在出现拥堵后，随着交通流密度的增加，本文模型求得的插入车辆数的误差逐渐增大.
2） 本文模型重构轨迹车辆位置的平均绝对误差在不同的交通流密度条件下均在可接受范围内，即本文模型在不同的交通流密度下均能较为准确地重构所有车辆的轨迹.
3） 重构轨迹的准确性随着CAV和CV渗透率的增加而提高. 与CV渗透率相比，CAV渗透率对结果的影响更大. 且当CAV渗透率较低时，本文模型也能较好地重构所有车辆的轨迹.
本文证明了基于跟驰特性的车辆轨迹重构模型的有效性，但选取的场景简单，仅研究了单车道高速公路车辆轨迹重构模型，未来将结合换道模型，研究智能网联环境下多车道车辆轨迹重构模型.
致谢：西南交通大学综合交通大数据应用技术国家工程实验室交大数科创新中心项目（JDSKCXZX202003）和重庆交通大学重庆市交通运输工程重点实验室开放课题（2018TE01）的资助.
-
图 4 不同车型振动加速度和动位移有效值对比
Figure 4. Comparison of effective values of acceleration and displacement under different train types
图 5 不同车速列车激励振动响应对比
Figure 5. Comparison of dynamic responses underdifferent train speeds.
图 9 模拟值与实测值对比（测点S2-3）
Figure 9. Comparison between the numerical results and the field measurements (Point S2-3)
图 11 基床及地基竖向动应力沿深度分布
Figure 11. Distribution of vertical dynamic stress along the depth of subgrade and foundation
图 12 过渡区钢轨位移和等效刚度分布
Figure 12. Distribution of the rail displacement and equivalent stiffness in the transition zone
图 13 列车经过过渡区时的竖向加速度分布
Figure 13. Vertical acceleration distribution of the train passing through the transition zone
表 1 车辆参数与扣件参数
Table 1. Vehicle parameters and fastener parameters
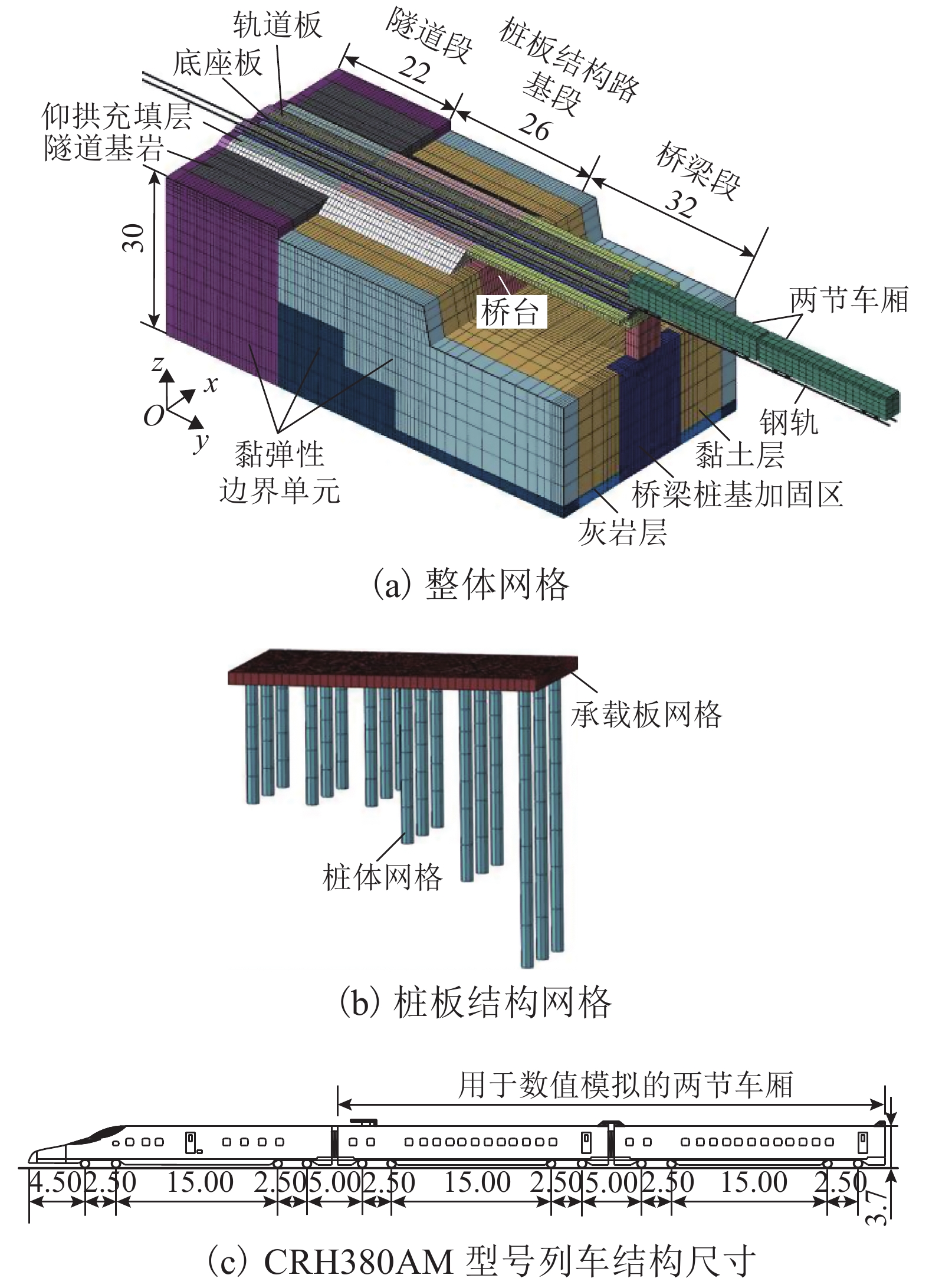
车体及扣件参数 数值 车体质量 Mv/kg 44 320 转向架质量 Mb/kg 3 136 轮对质量 Mw/kg 2 352 一系悬挂刚度 Kpz/（kN•m−1） 1 040 二系悬挂刚度 Ksz/（kN•m−1） 400 扣件刚度 Krz/（MN•m−1） 60 一系悬挂阻尼 Cpz/（kN•s•m−1） 40 二系悬挂阻尼 Csz/（kN•s•m−1） 60 扣件阻尼 Crz/（kN•s•m−1） 60 
下载: 导出CSV
表 2 过渡区各结构层材料属性
Table 2. Material properties of components in the transition zone
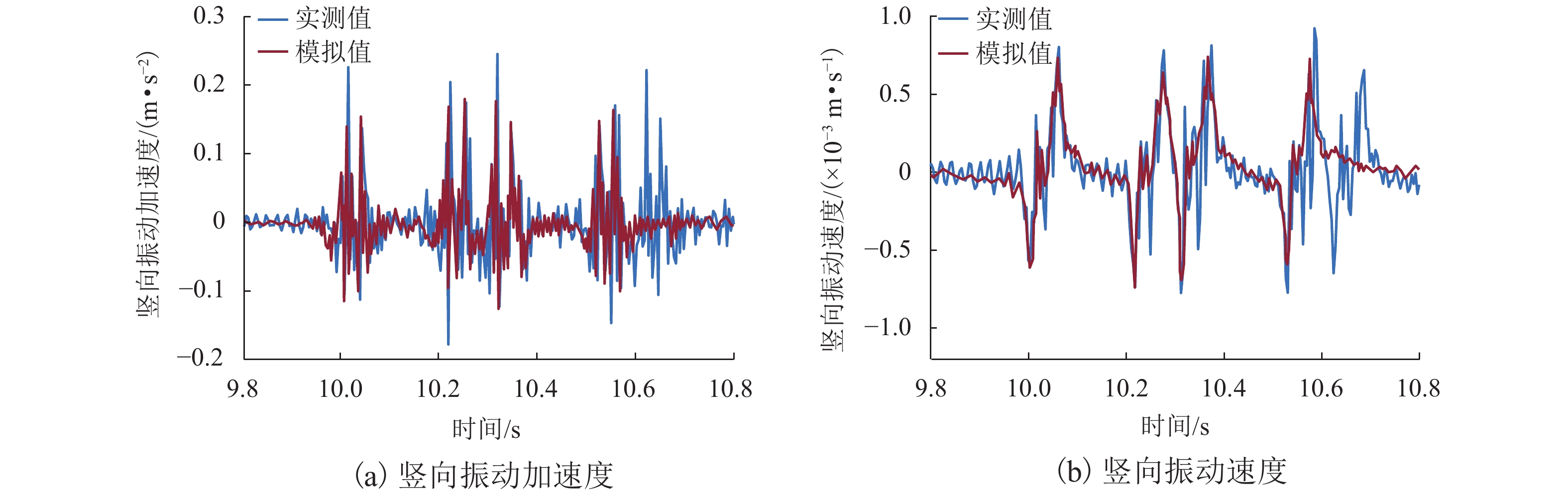
结构层 弹性模量/GPa 泊松比 密度/（kg•m−3） 黏聚力/kPa 内摩擦角/（°） 阻尼比 钢轨 205.900 0.30 7830 0.01 轨道板 32.500 0.16 2500 0.03 底座板 25.500 0.16 2500 0.03 基床表层 0.5400 0.30 2000 34 58 0.08 基床底层 0.920 0.25 2100 29 27 0.07 承载板 56.000 0.20 2500 0.02 钻孔桩 38.000 0.20 2500 0.03 粉质黏土 0.035 0.30 1930 24 16 0.10 灰岩 0.600 0.29 2090 0.09 桥台 30.000 0.20 2300 0.02 简支梁 22.000 0.18 2550 0.03 隧道基岩 12.000 0.20 2300 0.04
下载: 导出CSV
表 3 模拟值与实测值对比
Table 3. Comparison between the numerical results and the field measurements
项目名称 加速度 速度 实测值/（m•s−2） 模拟值/（m•s−2） 差异/% 实测值/
（× 10−3 m•s−1）模拟值/
（× 10−3 m•s−1）差异/% 底座板内侧测点 B0-3 0.190 0.170 10.5 0.940 0.89 5.3 S1-3 0.250 0.270 8.0 0.860 0.820 4.7 S2-3 0.170 0.160 5.9 0.800 0.690 13.8 S3-3 0.150 0.110 26.7 0.470 0.460 2.1 T0-3 0.460 0.250 45.6 1.420 0.930 34.5 路基中心线测点 B0-4 0.127 0.121 4.1 0.723 0.636 12.1 S1-4 0.114 0.129 13.1 0.391 0.357 8.8 S2-4 0.077 0.070 10.0 0.320 0.288 10.2 S3-4 0.071 0.055 23.0 0.247 0.209 15.5
下载: 导出CSV
-
[1] 苏谦, 罗照新, 王迅. 高速铁路路基非埋式桩板结构理论与实践[M]. 北京: 中国铁道出版社, 2011: 12-13. [2] 张树明,蒋关鲁,杜登峰,等. 新型桩板结构路基在季节冻土区的适用性[J]. 西南交通大学学报,2021,56(3): 541-549.ZHANG Shuming, JIANG Guanlu, DU Dengfeng, et al. Applicability of novel pile-plank embankment in seasonally frozen regions[J]. Journal of Southwest Jiaotong University, 2021, 56(3): 541-549. [3] 中华人民共和国铁道部. 铁路工程地基处理技术规程: TB 10106—2010[S]. 北京: 中国铁道出版社, 2010. [4] 詹永祥,蒋关鲁,牛国辉,等. 桩板结构路基动力模型试验研究[J]. 岩土力学,2008,29(8): 2097-2101,2110.ZHAN Yongxiang, JIANG Guanlu, NIU Guohui, et al. Model experimental research on dynamic performance of pile-plank embankment[J]. Rock and Soil Mechanics, 2008, 29(8): 2097-2101,2110. [5] 苏谦,王武斌,白皓,等. 非埋式桩板结构路基承载机制[J]. 交通运输工程学报,2012,12(1): 19-24.SU Qian, WANG Wubin, BAI Hao, et al. Bearing capacity mechanism of non-embedded pile-plank structure subgrade[J]. Journal of Traffic and Transportation Engineering, 2012, 12(1): 19-24. [6] 梁波,邓剑辰. 桩板结构路基的动力响应分析[J]. 铁道学报,2008,30(5): 80-84.LIANG Bo, DENG Jianchen. Analysis on dynamic responses of subgrade with the pile-plank structure[J]. Journal of the China Railway Society, 2008, 30(5): 80-84. [7] 马坤全. 高速行车条件下桩板结构-地基土系统的空间振动性能分析[J]. 铁道学报,2013,35(1): 93-100.MA Kunquan. Analysis on space vibration performance of pile-plank structure-foundation soil system under the condition of high-speed trains running[J]. Journal of the China Railway Society, 2013, 35(1): 93-100. [8] 苏谦,白皓,黄俊杰,等. 埋入式连续桩板结构温度效应计算方法[J]. 西南交通大学学报,2012,47(2): 181-186.SU Qian, BAI Hao, HUANG Junjie, et al. Calculation method for embedded continuous pile-board structure under thermal stresses[J]. Journal of Southwest Jiaotong University, 2012, 47(2): 181-186. [9] 国家铁路局. 高速铁路设计规范: TB 10621—2014[S]. 北京: 中国铁道出版社, 2014. [10] 魏丽敏, 何重阳, 杨哲. 沪昆铁路客运专线南昌西至宜春东段高速综合试验研究报告[R]. 长沙: 中南大学, 2014. [11] PAIXAO A, FORTUNATO E, CALCADA R. Transition zones to railway bridges:track measurements and numerical modelling[J]. Engineering Structures, 2014, 80: 435-443. doi: 10.1016/j.engstruct.2014.09.024 [12] 瀚邦. 峰值、有效值和平均值的使用[J]. 噪声与振动控制,1984(3): 26. [13] ANG K K, DAI J. Response analysis of high-speed rail system accounting for abrupt change of foundation stiffness[J]. Journal of Sound and Vibration, 2013, 332(12): 2954-2970. [14] SANUDO R, CERRADA M, ALONSO B, et al. Analysis of the influence of support positions in transition zones. a numerical analysis[J]. Construction and Building Materials, 2017, 145: 207-217. doi: 10.1016/j.conbuildmat.2017.03.204 [15] LI D, SELIG E T. Method for railroad track foundation design. I:development[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(4): 316-322. doi: 10.1061/(ASCE)1090-0241(1998)124:4(316) [16] ZHAI W M, SUN X. A detailed model for investigating vertical interactions between railway vehicle and track[J]. Vehicle System Dynamics, 1994, 23: 603-615. doi: 10.1080/00423119308969544 [17] 刘文劼,梅慧浩,冷伍明,等. 路基基床动应力响应特征的数值模拟研究[J]. 铁道学报,2017,39(12): 108-1.LIU Wenjie, MEI Huihao, LENG Wuming, et al. Numerical analysis of dynamic stress response characteristics of subgrade bed[J]. Journal of the China Railway Society, 2017, 39(12): 108-1. [18] 薛富春,张建民. 移动荷载下高铁路基段振动加速度频谱衰减特性[J]. 岩土力学,2015,36(增刊1): 445-451.XUE Fuchun, ZHANG Jianming. Attenuations of acceleration spectra of high-speed railway embankment subjected to moving loads[J]. Rock and Soil Mechanics, 2015, 36(S1): 445-451. [19] HU P, ZHANG C, WEN S, et al. Dynamic responses of high-speed railway transition zone with various subgrade fillings[J]. Computers and Geotechnics, 2019, 108: 17-26. doi: 10.1016/j.compgeo.2018.12.011 [20] 聂志红,阮波,李亮. 秦沈客运专线路堑段基床结构动态测试分析[J]. 振动与冲击,2005,24(2): 30-32,146.NIE Zhihong, RUAN Bo, LI Liang. Testing and analysis on dynamic performance of subgrade of QingShen Railway[J]. Journal of Vibration and Shock, 2005, 24(2): 30-32,146. [21] 郭志广,魏丽敏,何群,等. 武广高速铁路无砟轨道路基动力响应试验研究[J]. 振动与冲击,2013,32(14): 148-152,163.GUO Zhiguang, WEI Limin, HE Qun, et al. Tests for dynamic response of ballastless track subgrade of wu-guang high-speed railway[J]. Journal of Vibration and Shock, 2013, 32(14): 148-152,163. [22] ESVELD C. Modern railway track[M]. Zaltbommel: MRT-Production, 2001: 480-481. [23] 陈小平,王平. 时速350 km客运专线无砟道岔的合理轨道刚度研究[J]. 铁道标准设计,2010(3): 1-3.CHEN Xiaoping, WANG Ping. Study on reasonable orbital stiffness of ballastless turnouts in passenger dedicated lines with a speed of 350km/h[J]. Railway Standard Design, 2010(3): 1-3. [24] 蔡成标,徐鹏. 弹性支承块式无砟轨道结构参数动力学优化设计[J]. 铁道学报,2011,33(1): 69-75.CAI Chengbiao, XU Peng. Dynamic optimization design of the structural parameters of low vibration track[J]. Journal of the China Railway Society, 2011, 33(1): 69-75. [25] 铁道部标准计量研究所. 铁道机车动力学性能试验鉴定方法及评定标准: TBT 2360—1993[S]. 北京: 中华人民共和国铁道部, 1993. 期刊类型引用(15)
1. 甘建，王晓明，杨光，朱翔宇，黄乐乐. 钢管连接卯榫接缝预制拼装桥墩抗震性能分析. 公路. 2024(05): 233-239 . 
百度学术2. 欧智菁，曹磊，林上顺，薛文浩，陈治雄. 装配式方钢管约束混凝土桥墩恢复力模型研究. 应用力学学报. 2024(03): 612-620 . 百度学术3. 林上顺，何乐，夏樟华，秦志清，张乐彤，陈治雄. 榫卯-灌浆套筒混合连接装配式方墩轴压性能研究. 重庆大学学报. 2024(06): 58-67 . 百度学术4. 林上顺，张建帅，夏樟华，叶世集，赵锦冰. 装配式RC桥墩研究现状及展望. 土木与环境工程学报(中英文). 2024(06): 135-147 . 百度学术5. 欧智菁，颜建煌，俞杰，林上顺. 装配式圆钢管约束混凝土桥墩抗震试验及计算方法研究. 土木工程学报. 2023(01): 77-89 . 百度学术6. 林上顺，林永捷，夏樟华，林长庚，赵锦冰. UHPC和预制榫卯混合连接装配式RC桥墩拟静力试验. 桥梁建设. 2023(01): 16-23 . 百度学术7. 欧智菁，曹磊，薛文浩. 混合接头装配式方钢管约束混凝土桥墩抗震性能研究. 桥梁建设. 2023(01): 40-47 . 百度学术8. 孟凌霄，孙中华，朱志鑫，许英东，张传平，付涛. 中空夹层预制装配式圆形桥墩抗震性能参数分析. 建筑科学与工程学报. 2023(05): 138-147 . 百度学术9. 欧智菁，陈玮悦，林上顺，薛文浩. 方钢管约束混凝土桥墩拟静力试验. 重庆大学学报. 2023(10): 40-50 . 百度学术10. 林上顺，林永捷，夏樟华，赵锦冰，黎雅乐. 现浇ECC和预制榫卯混合连接装配式RC桥墩抗震性能. 交通运输工程学报. 2023(05): 104-117 . 百度学术11. 夏樟华，林龙镁，林上顺，张伟，姜绍飞. 灌浆套筒混合连接装配式方柱墩偏压性能试验. 沈阳建筑大学学报(自然科学版). 2022(01): 24-32 . 百度学术12. 林上顺，何乐，夏樟华，张乐彤，叶世集，陈治雄. 榫卯-灌浆套筒混合连接装配式方墩轴压承载力. 郑州大学学报(工学版). 2022(03): 67-72 . 百度学术13. 林上顺，林永捷，夏樟华，杨切，叶世集. 不同拼接构造的装配式圆柱墩偏压性能试验. 工业建筑. 2022(04): 91-97 . 百度学术14. 欧智菁，颜建煌，俞杰，林上顺，秦志清. 装配式圆钢管约束混凝土桥墩抗震性能研究. 振动与冲击. 2022(18): 47-54 . 百度学术15. 林上顺，叶世集，夏樟华，杨切，欧智菁. 采用混合接头的装配式RC圆柱墩轴压极限承载力试验研究. 武汉大学学报(工学版). 2022(12): 1221-1228 . 百度学术其他类型引用(4)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 468
- HTML全文浏览量: 343
- PDF下载量: 29
- 被引次数: 19