Experimental Study on Coefficient Value of Subgrade Reaction in Seismic Analysis of Underground Structures
-
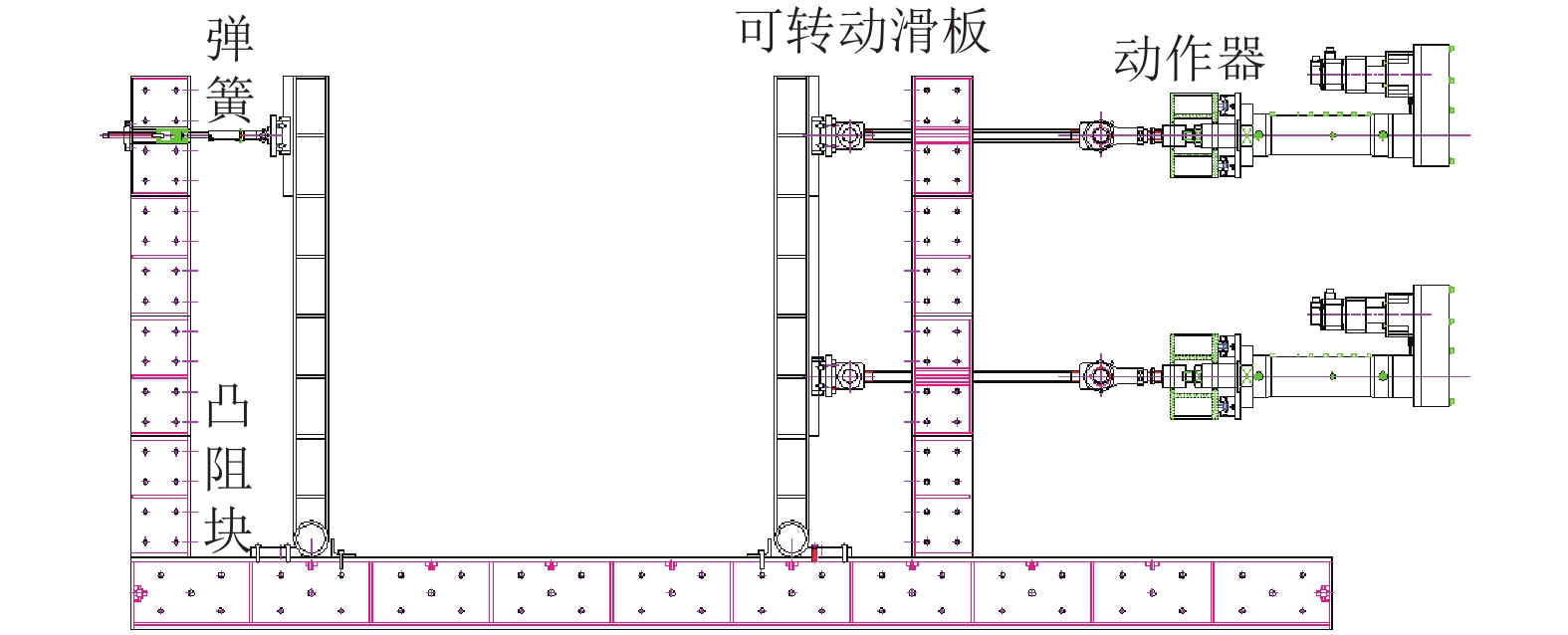
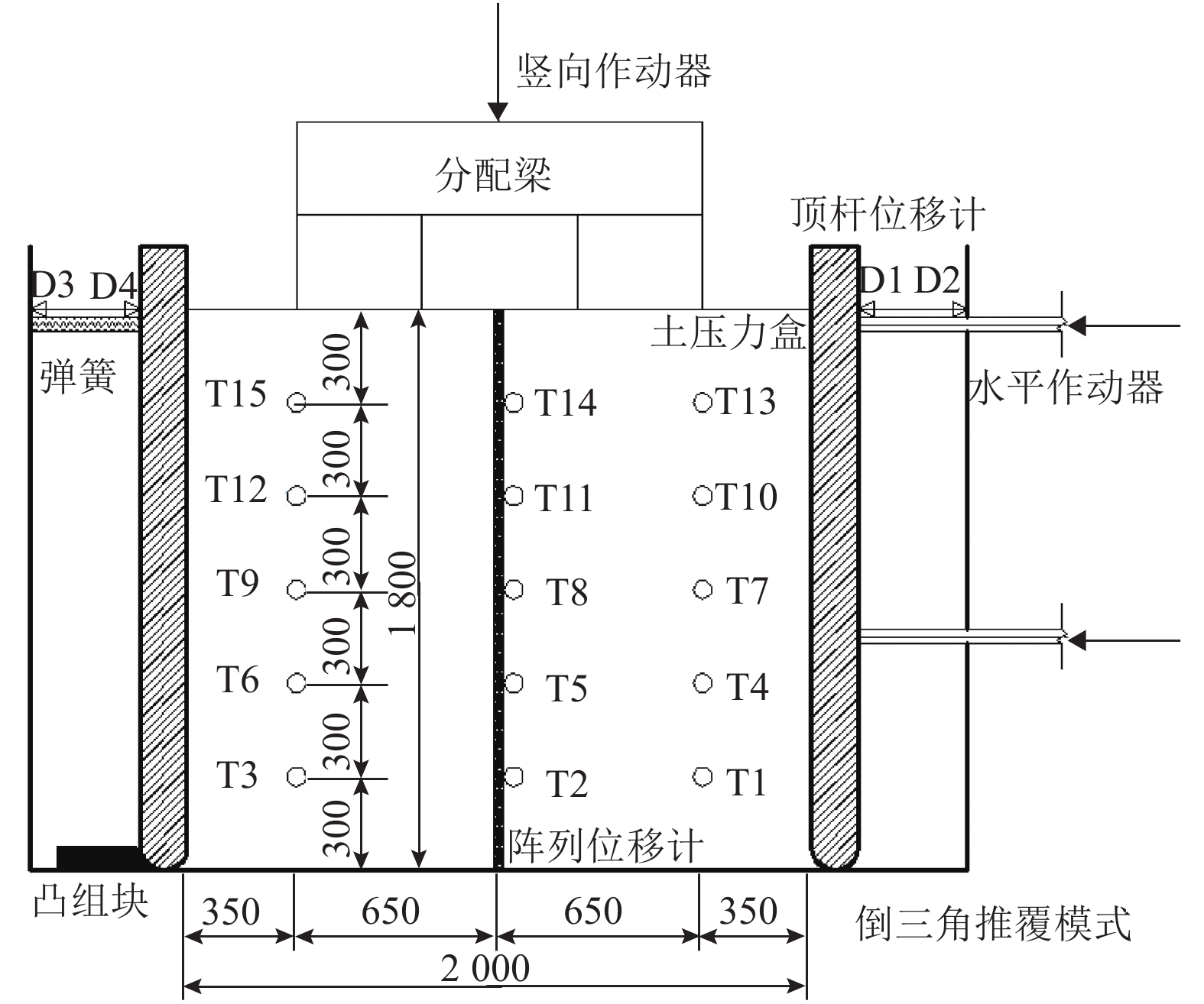
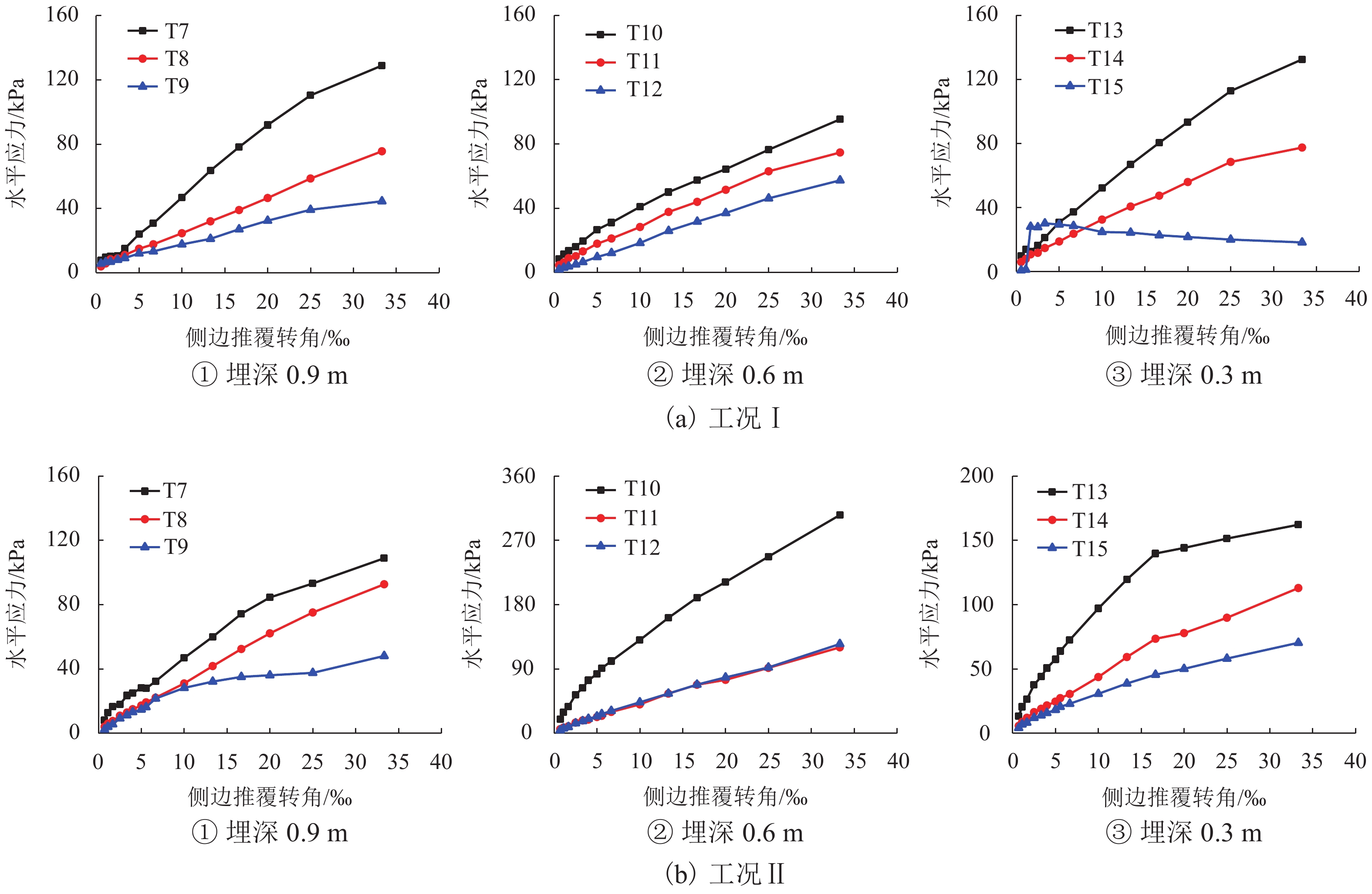
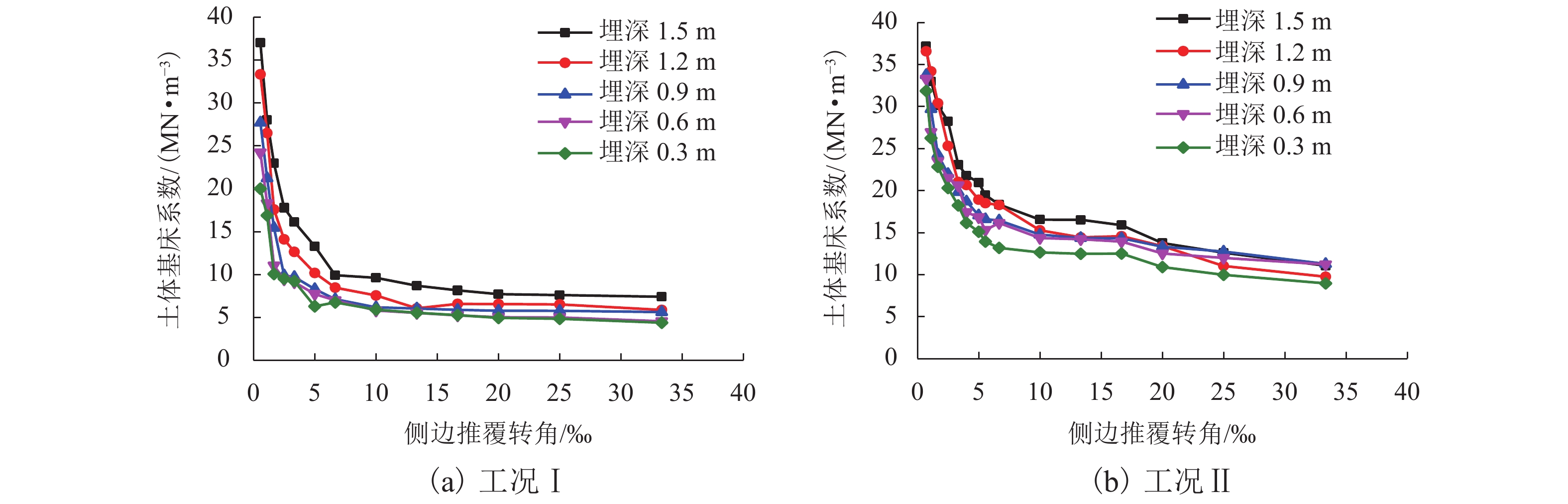
摘要: 在对地下结构进行抗震分析时,基床系数的准确性直接决定了反应位移法的计算精度. 针对基床系数相关研究的不足,提出了一种拟静力试验法,自主研发了大型拟静力模型箱,围绕砂土场地开展了有无轴压两组试验;在此基础上,提出了基床系数沿深度修正法,并进行了算例验证. 结果表明:水平基床系数随推覆水平的增大而减小,随土层深度的增大而增大;附加应力对基床系数取值存在较大影响;采用修正基床系数可显著提高反应位移法的计算精度,较规范中基床系数静力有限元法,地下结构弯矩误差最大可由16.7%降低至9.1%,顶底板相对位移的计算误差可由35.0%降低至18.8%,验证了该新型室内基床系数测试方法的可行性及基床系数沿深度修正法的合理性.Abstract: In seismic analysis of underground structures, the precision of the coefficient of subgrade reaction directly determines the accuracy of response displacement method. Considering the deficiencies of relevant research on the coefficient of subgrade reaction, a quasi-static test method was proposed, a large quasi-static model box was developed, and two groups of tests with and without axial load in sandy soil were carried out. On this basis, a correction method for the coefficient of subgrade reaction along depth is proposed and verified by an example. Results indicate that the horizontal coefficient of subgrade reaction decreases with an increase in the pushover level and increases with the soil depth. Moreover, the additional stress has great influence on the coefficient value; using modified coefficient can significantly improve the accuracy of the response displacement method. Compared with the result adopting the coefficient in terms of static finite element method in the code, the maximum bending moment error of the underground structure can be reduced from 16.7% to 9.1%, and the relative displacement error between roof and floor can be reduced from 35.0% to 18.8%. Thus, the feasibility of the new coefficient measuring method and the rationality of the coefficient modified method are validated.
-
表 1 深度修正系数
Table 1. Depth correction factor
工况 埋深/mm 300 600 900 1 200 1 500 Ⅰ 0.848 0.888 1 1.183 1.457 Ⅱ 0.866 0.967 1 1.062 1.131 表 2 两种方法所得基床系数值
Table 2. Coefficient values of subgrade reaction by two methods
MN•m−3 反向位移法 侧边基床系数 顶部基床系数 底部基床系数 正向 切向 正向 切向 正向 切向 1 33.5 23.8 12.4 13.7 56.9 43.5 2 11.1~55.3 7.9~39.3 12.4 13.7 56.9 43.5 表 3 地下结构地震反应计算结果
Table 3. Seismic response calculation results of underground structure
方法类型 弯矩/(kN•m) 弯矩误差/% 顶底板相对位移/mm 位移误差/% 点 A 点 B 点 A 点 B 动力时程分析 347.5 340.6 4.144 反应位移法 1 291.8 16.0 283.7 16.7 2.694 35.0 反应位移法 2 315.3 9.3 309.6 9.1 3.366 18.8 -
程新俊,景立平,崔杰,等. 不同场地沉管隧道振动台模型试验研究[J]. 西南交通大学学报,2017,52(6): 1113-1120.CHENG Xinjun, JING Liping, CUI Jie, et al. Research of shaking table model tests on immersed tunnels under different conditions[J]. Journal of Southwest Jiaotong University, 2017, 52(6): 1113-1120. HASHASH Y M A, HOOK J J, SCHMIDT B, et al. Seismic design and analysis of underground structures[J]. Tunnelling and Underground Space Technology, 2001, 16(4): 247-293. doi: 10.1016/S0886-7798(01)00051-7 川岛一彦. 地下构筑物の耐震设计[M]. 茨城: 鹿岛出版社, 1994: 11-26. 中华人民共和国国家标准. 核电厂抗震设计规范: GB 50267—1997[S]. 北京: 中国标准出版社, 1997. 中华人民共和国国家标准. 城市轨道交通结构抗震设计规范: GB 50909—2014[S]. 北京: 中国计划出版社, 2014. Japan Society of Civil Engineers. Earthquake resistant design codes in Japan[S]. Tokyo: Waco Co., Ltd., 2000. 朱令,丁文其,王瑞,等. 考虑成层土变异性的等效基床系数分析[J]. 岩石力学与工程学报,2014,33(S1): 3036-3041.ZHU Ling, DING Wenqi, WANG Rui, et al. Analysis of equivalent coefficient of subgrade reaction considering variability of layered soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(S1): 3036-3041. 李英民,王璐,刘阳冰,等. 地下结构抗震计算地基弹簧系数取值方法研究[J]. 地震工程与工程振动,2012,32(1): 106-113.LI Yingmin, WANG Lu, LIU Yangbing, et al. Analysis of methods for determining the spring constant of ground foundationin seismic design of underground structures[J]. Journal of Earthquake Engineering and Engineering Vibration, 2012, 32(1): 106-113. NAEINI S A, TAHERABADI E. Numerical and theoretical study of plate load test to define coefficient of subgrade reaction[J]. Journal of Geotechnical and Transportation Engineering, 2015, 1(2): 38-42. 刘益平,孙焯. 基床系数试验测试与取值方法比选[J]. 电力勘测设计,2018(增刊1): 130-135.LIU Yiping, SUN Chao. Comparison of test and evaluation methods of coefficient of subgrade reaction[J]. Electric Power Survey and Design, 2018(S1): 130-135. 韩相超,雷醒民,吕远强. 渭北黄土塬地基土基床系数空间分布规律探索[J]. 陕西煤炭,2016,35(2): 51-55.HAN Xiangchao, LEI Xingmin, LYU Yuanqiang. Research on the spatial distribution of subgrade coefficient of the foundation soil in Weibei loess tableland[J]. Shanxi Coal, 2016, 35(2): 51-55. 王沛,魏丽,王晓燕,等. 旁压试验在车站基坑工程勘察中应用[J]. 土工基础,2019,33(2): 228-231.WANG Pei, WEI Li, WANG Xiaoyan, et al. Application of pressuremeter tests in the geotechnical investigations of a metro station[J]. Soil Engineering and Foundation, 2019, 33(2): 228-231. 牛真茹,李飞飞,庞炜. 合肥地区黏性土基床系数分布规律及相关性研究[J]. 铁道勘察,2018,44(4): 87-89.NIU Zhenru, LI Feifei, PANG Wei. Study on distribution and correlation analysis of reaction coefficient of subgrade cohesive soil in Hefei area[J]. Railway Investigation and Surveying, 2018, 44(4): 87-89. BURHAN A, AYHAN G. Modulus of subgrade reaction that varies with magnitude of displacement of cohesionless soil[J]. Arabian Journal of Geosciences, 2018, 11(13): 351-358. doi: 10.1007/s12517-018-3713-1 禹海涛,张正伟,朱春成,等. 关于反应位移法中地层变形模式的讨论[J]. 结构工程师,2018,34(2): 145-151.YU Haitao, ZHANG Zhengwei, ZHU Chuncheng, et al. Discussion on the ground deformation mode in response displacement method[J]. Structural Engineers, 2018, 34(2): 145-151. 中华人民共和国国家标准. 城市轨道交通岩土工程勘察规范: GB 50307—2012[S]. 北京: 中国计划出版社, 2012. -





 下载:
下载: