Rapid Identification Method for Lithology of Tunnel Based on Lightweight Model
-
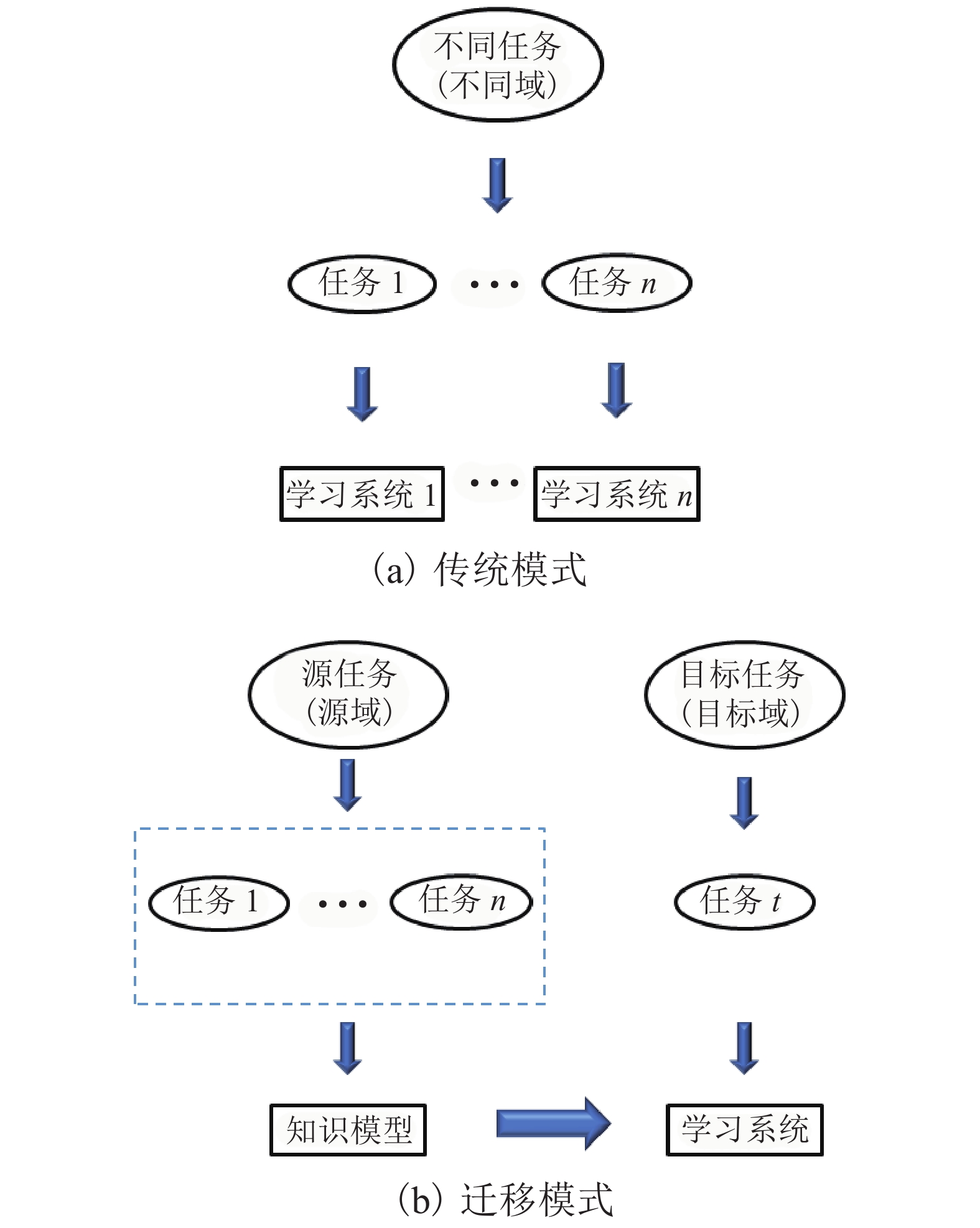
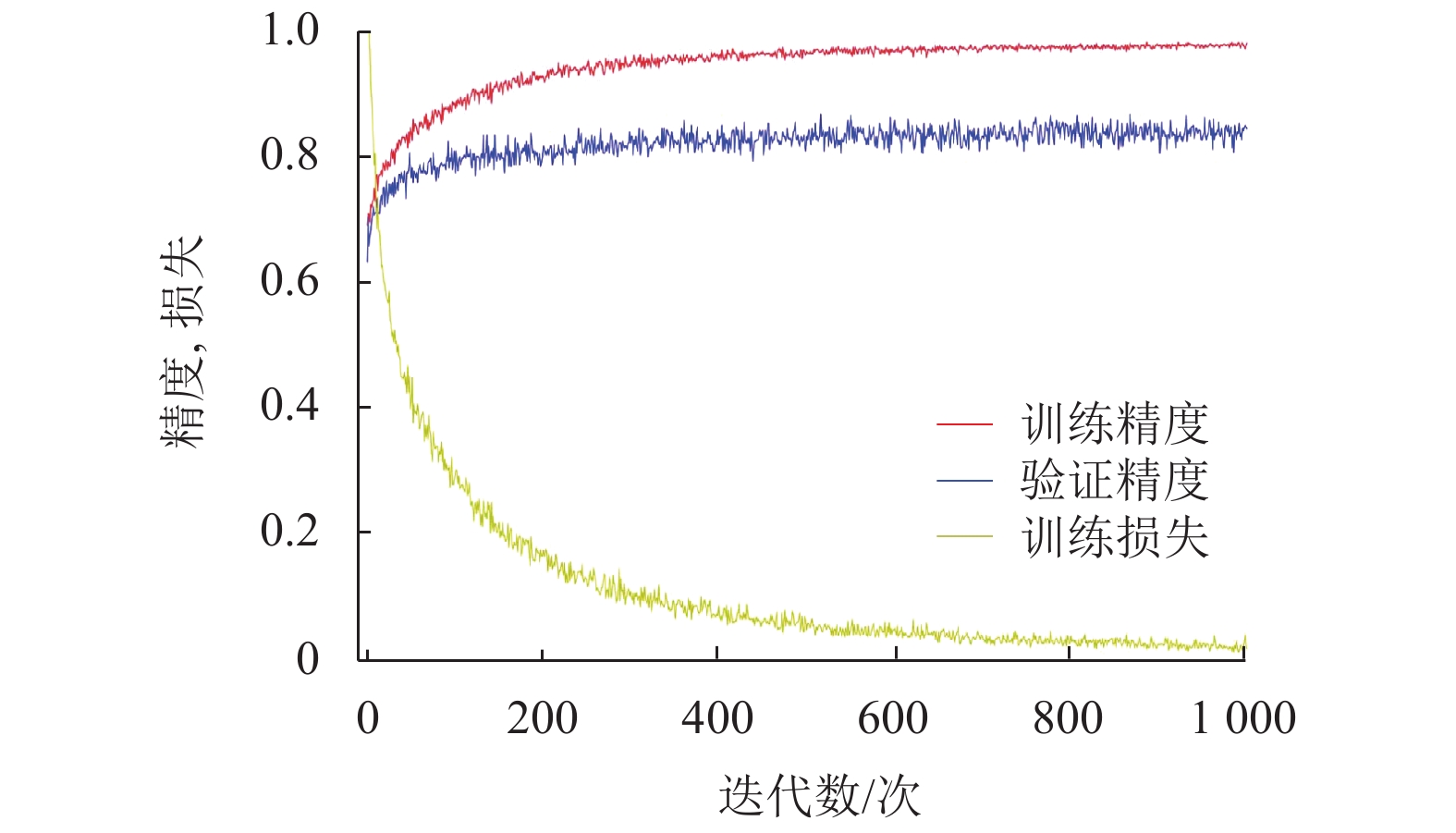
摘要: 为了解决隧道岩性现有识别方法中识别时间长、安全性低、主观性大等问题，结合不同岩性表面具有不同的成分特征，提出了一种基于轻量级模型与岩石图像的隧道岩性快速识别方法. 首先，通过相机采集隧道常见的片麻岩、花岗岩、石灰岩、大理岩、凝灰岩、砂岩等6类主要岩石，建立了岩石图像数据集并划分训练集、验证集与测试集；然后，基于轻量级模型MobileNet V2在ImageNet数据集上进行预训练，改进模型分类器结构以适应岩石数据集，并采用模型迁移学习训练方法对1170张训练集图像进行训练，获取了岩石岩性识别模型；最后，选取共计300张测试集图像在离线条件下进行了模型测试，并与VGG16模型与SVM （support vector machine）模型进行了对比. 实验结果表明：模型在测试数据集上的各项总体评估指标均在85%以上，其中凝灰岩各项评价指标达到94%以上，模型大小仅28.3 MB，平均识别时间为2880 ms，表明该识别模型体积小，识别准确率高，识别时间快，在精确率与识别速度上均优于传统方法.Abstract: In order to solve the problems of long identification time, low security, and high subjectivity in the existing identification methods of tunnel lithology, given the fact that composition characteristics differ among lithological surfaces, a rapid identification method of tunnel lithology based on the lightweight model and rock images was proposed. First, six types of major rocks in tunnels, including gneiss, granite, limestone, marble, tuff and sandstone, were collected by camera, and the rock image data set was established and divided into training set, verification set and test set. Then, based on the lightweight model MobileNet V2, pre-training was conducted on the ImageNet data set, the structure of the model classifier was improved to adapt to the rock data set, and 1170 images of the training set were trained using the transfer learning method for model training to obtain the rock lithology recognition model. Finally, a total of 300 test set images were selected and tested offline, and compared with those of the VGG16 model and the SVM (support vector machine) model. The experimental results show that the overall evaluation indexes of the model on the test data set were above 85%, of which the evaluation indexes of tuff reached more than 94%, the size of the model was only 28.3 MB, and the average recognition time was 2880 ms, indicating that the recognition model was small in size, high in recognition accuracy, and fast in recognition time, which is superior to traditional methods in accuracy and recognition speed.
-
Key words:
- lightweight model /
- transfer learning /
- rock image /
- lithology identification
-
图 6 MobileNet V2深度可分离式卷积结构
Figure 6. MobileNet V2 depthwise separable convolution structure
图 7 训练中训练精度、验证精度及损失变化
Figure 7. Training accuracy，verification accuracy and loss changes during training
表 1 MobileNet V2基础结构
Table 1. MobileNet V2 basic structure
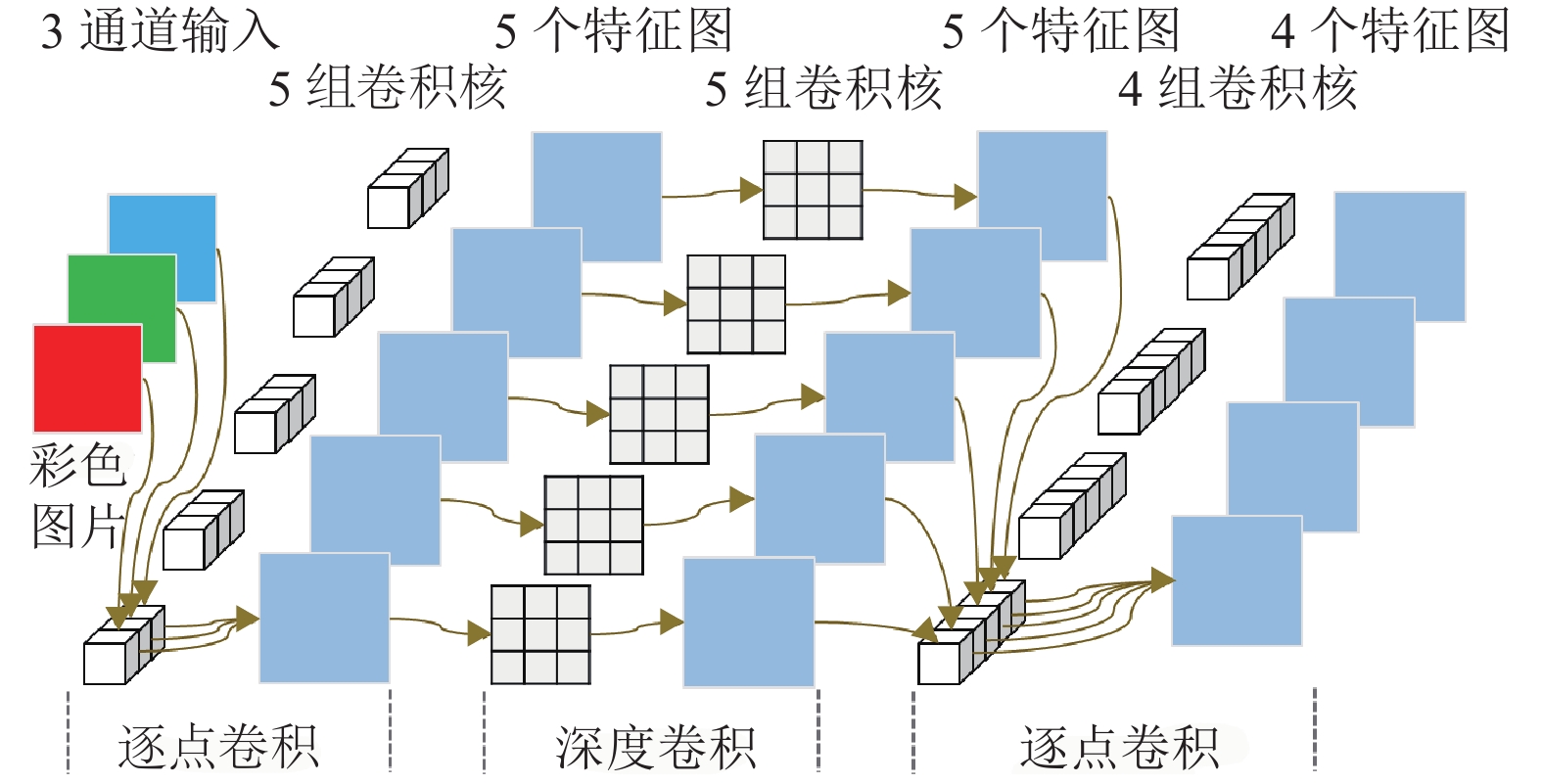
输入 操作 t c n s 2242 × 3 conv2d 32 1 2 1122 × 32 bottleneck 1 16 1 1 1122 × 16 bottleneck 6 24 2 2 562 × 24 bottleneck 6 32 3 2 282 × 32 bottleneck 6 64 4 2 142 × 64 bottleneck 6 96 3 1 142 × 96 bottleneck 6 160 3 2 72 × 160 bottleneck 6 320 1 1 72 × 320 conv2d 1 × 1 1280 1 1 72 × 1280 avgpool 7 × 7 1 1 × 1 × 1280 conv2d 1000 注：c 为输出通道数；s 为模块第 1 次重复时的操作步长（之后重复操作步长均为 1）. 
下载: 导出CSV
表 2 改进的模型结构
Table 2. Improved model structure
输入 操作 输出 224 × 224 × 3 conv2d 112 × 112 × 32 112 × 112 × 32 bottleneck1 112 × 112 × 16 $ \vdots $ $\vdots $ $\vdots $ 7 × 7 × 160 bottleneck16 7 × 7 × 160 7 × 7 × 160 bottleneck17 7 × 7 × 320 7 × 7 × 320 conv2d 1 × 1 7 × 7 × 1280 7 × 7 × 1280 avgpool 7 × 7 1 × 1 × 1280 1 × 1 × 1280 Dense1 （激活函数 Relu） 1 × 1 × 1024 1 × 1 × 1024 Dropout 1 × 1 × 1024 1 × 1 × 1024 Dense2 （激活函数 Relu） 1 × 1 × 256 1 × 1 × 256 Dropout 1 × 1 × 256 1 × 1 × 256 Dense3 （激活函数 Relu） 1 × 1 × 6 1 × 1 × 6 Softmax 分类函数 分类结果
下载: 导出CSV
表 3 基于fine-tune的迁移训练
Table 3. Transfer training based on fine-tune
输入 操作 输出 224 × 224 × 3 conv2d 112 × 112 × 32 112 × 112 × 32 bottleneck1 112 × 112 × 16 $ \vdots $ $\vdots $ $\vdots $ 7 × 7 × 160 bottleneck16 7 × 7 × 160 7 × 7 × 160 bottleneck17 7 × 7 × 320 7 × 7 × 320 conv2d 1 × 1 7 × 7 × 1280 7 × 7 × 1280 avgpool 7 × 7 1 × 1 × 1280 1 × 1 × 1280 Dense （激活函数 Relu） 1 × 1 × 1024 1 × 1 × 1024 Dropout 1 × 1 × 1024 1 × 1 × 1024 Dense （激活函数 Relu） 1 × 1 × 256 1 × 1 × 256 Dropout 1 × 1 × 256 1 × 1 × 256 Dense （激活函数 Relu） 1 × 1 × 6 1 × 1 × 6 Softmax 分类函数 分类结果
下载: 导出CSV
表 4 训练集各项评价指标
Table 4. Index values for training set evaluation
岩石 精确率 召回率 综合评价指标 片麻岩 1.000 0.933 0.965 花岗岩 1.000 0.967 0.983 大理岩 0.938 1.000 0.968 石灰岩 0.935 0.967 0.951 凝灰岩 0.968 1.000 0.984 砂岩 1.000 0.967 0.983
下载: 导出CSV
表 5 测试集图片识别结果
Table 5. Recognition results for testing set images
张 测试图片 片麻岩 花岗岩 大理岩 石灰岩 凝灰岩 砂岩 片麻岩 36 2 5 6 1 花岗岩 45 1 4 大理岩 1 46 3 石灰岩 4 45 1 凝灰岩 2 48 砂岩 4 3 1 4 2 36 合计 40 51 57 64 51 37
下载: 导出CSV
表 6 测试集各项评价指标
Table 6. Index values for testing set evaluation
岩石 P R F1 片麻岩 0.900 0.720 0.800 花岗岩 0.882 0.900 0.891 大理岩 0.807 0.920 0.860 石灰岩 0.703 0.900 0.789 凝灰岩 0.941 0.960 0.950 砂岩 0.973 0.720 0.828
下载: 导出CSV
表 7 实验结果对比
Table 7. Comparison of experimental results
分类指标 平均识别精确率 单张识别时间/ms SVM 0.665 4650 VGG16 0.814 3680 MobileNet V2 0.868 2880
下载: 导出CSV
-
管会生,吴和北,陶伟,等. 深埋斜井隧道双模式盾构刀盘驱动扭矩分析[J]. 现代隧道技术,2015,52(6): 163-169.GUAN Huisheng, WU Hebei, TAO Wei, et al. Analysis of the cutterhead driving torque of a dual-mode shield used for a deeply buried inclined shaft[J]. Modern Tunnelling Technology, 2015, 52(6): 163-169. 刘书斌, 方勇, 周超月, 等. 承压溶腔对隧道开挖稳定性影响的模型试验[J]. 岩石力学与工程学报, 2017, 36(增刊2): 3781-3791.LIU Shubin, FANG Yong, ZHOU Chaoyue, et al. Model test of tunnel excavation stability influenced by concealed cave with internal water pressure[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(S2): 3781-3791. 严鹏,张晨,高启栋,等. 不同损伤程度下岩石力学参数变化的声波测试[J]. 岩土力学,2015,36(12): 3425-3432.YAN Peng, ZHANG Chen, GAO Qidong, et al. Acoustic wave test on mechanical properties variation of rocks under different damage degrees[J]. Rock and Soil Mechanics, 2015, 36(12): 3425-3432. 苏凯,张妍珺,伍鹤皋,等. 隧洞开挖过程中围岩安全系数演化特征与支护时机选择方法研究[J]. 岩石力学与工程学报,2019,38(增刊1): 2964-2975.SU Kai, ZHANG Yanjun, WU Hegao, et al. Evolution of surrounding rock safety factor and support installation time during tunnel excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(S1): 2964-2975. WEI X S, QIN X H, RONG C L, et al. Image classification recognition for rock micro-thin section based on probabilistic neural networks[J]. Applied Mechanics and Materials, 2014, 602-605: 2147-2152. doi: 10.4028/www.scientific.net/AMM.602-605.2147 罗佳,刘大刚. 基于自适应阈值和连通域的隧道裂缝提取[J]. 西南交通大学学报,2018,53(6): 1137-1141. doi: 10.3969/j.issn.0258-2724.2018.06.007LUO Jia, LIU Dagang. Tunnel crack extraction based on adaptive threshold and connected domain[J]. Journal of Southwest Jiaotong University, 2018, 53(6): 1137-1141. doi: 10.3969/j.issn.0258-2724.2018.06.007 刘烨,程国建,马微,等. 基于铸体薄片图像颜色空间与形态学梯度的岩石分类[J]. 中南大学学报(自然科学版),2016,47(7): 2375-2382.LIU Ye, CHENG Guojian, MA Wei, et al. Rock classification based on features form color space and morphological gradient of rock thin section image[J]. Journal of Central South University (Science and Technology), 2016, 47(7): 2375-2382. 程国建,郭文惠,范鹏召. 基于卷积神经网络的岩石图像分类[J]. 西安石油大学学报(自然科学版),2017,32(4): 116-122. doi: 10.3969/j.issn.1673-064X.2017.04.020CHENG Guojian, GUO Wenhui, FAN Pengshao. Study on rock image classification based on convolution neural network[J]. Journal of Xi’an Shiyou University (Natural Science Edition), 2017, 32(4): 116-122. doi: 10.3969/j.issn.1673-064X.2017.04.020 LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521: 436-444. doi: 10.1038/nature14539 BIANCO S, BUZZELLI M, MAZZINI D, et al. Deep learning for logo recognition[J]. Neurocomputing, 2017, 245: 23-30. doi: 10.1016/j.neucom.2017.03.051 侯进,吕志良,徐茂,等. 基于深度学习的复合神经网络机场信号检测框架[J]. 西南交通大学学报,2019,54(4): 863-869.HOU Jin, LYU Zhiliang, XU Mao, et al. Combined neural networks based on deep learning for signal detection in aeronautical communications[J]. Journal of Southwest Jiaotong University, 2019, 54(4): 863-869. 白林,姚钰,李双涛,等. 基于深度学习特征提取的岩石图像矿物成分分析[J]. 中国矿业,2018,27(7): 178-182.BAI Lin, YAO Yu, LI Shuangtao, et al. Mineral composition analysis of rock image based on deep learning feature extraction[J]. China Mining Magazine, 2018, 27(7): 178-182. 徐述腾,周永章. 基于深度学习的镜下矿石矿物的智能识别实验研究[J]. 岩石学报,2018,34(11): 3244-3252.XU Shuteng, ZHOU Yongzhang. Artificial intelligence identification of ore minerals under microscope based on deep learning algorithm[J]. Acta Petrologica Sinica, 2018, 34(11): 3244-3252. IMAMVERDIYEV Y, SUKHOSTAT L. Lithological facies classification using deep convolutional neural network[J]. Journal of Petroleum Science and Engineering, 2019, 174: 216-228. doi: 10.1016/j.petrol.2018.11.023 ZHANG Y, WANG G, LI M, et al. Automated classification analysis of geological structures based on images data and deep learning model[J]. Applied Sciences, 2018, 8(12): 2493. doi: 10.3390/app8122493 PAN S J, YANG Q. A survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345-1359. doi: 10.1109/TKDE.2009.191 QURESHI A S, KHAN A, ZAMEER A, et al. Wind power prediction using deep neural network based meta regression and transfer learning[J]. Applied Soft Computing, 2017, 58: 742-755. doi: 10.1016/j.asoc.2017.05.031 张野,李明超,韩帅. 基于岩石图像深度学习的岩性自动识别与分类方法[J]. 岩石学报,2018,34(2): 333-342.ZHANG Ye, LI Mingchao, HAN Shuai. Automatic identification and classification in lithology based on deep learning in rock images[J]. Acta Petrologica Sinica, 2018, 34(2): 333-342. LI N, HAO H, GU Q, et al. A transfer learning method for automatic identification of sandstone microscopic images[J]. Computers & Geosciences, 2017, 103: 111-121. WANG C, LI Y, FAN G, et al. Quick recognition of rock images for mobile applications[J]. Journal of Engineering Science and Technology Review, 2018, 11(4): 111-117. doi: 10.25103/jestr.114.14 SANDLER M, HOWARD A, ZHU M, et al. MobileNet V2: inverted residuals and linear bottlenecks[C]//IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 4510-4520. CHOLLET F. Xception: deep learning with depthwise separable convolutions[C]//IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 1800-1807. PAN S J, TSANG I W, KWOL J T, et al. Domain adaptation via transfer component analysis[J]. IEEE Transactions on Neural Networks, 2011, 22(2): 199-210. doi: 10.1109/TNN.2010.2091281 HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]//IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770-778. 杜恩宇,张宁,李艳荻. 基于自适应分块编码SVM的车道导向箭头多分类方法[J]. 光学学报,2018,38(10): 251-258.DU Enyu, ZHANG Ning, LI Yandi. Multi classification method of lane arrow markings based on support vector machines with adaptive partitioning coding[J]. Acta Optica Sinica, 2018, 38(10): 251-258. -
下载:
点击查看大图
图(7) / 表(7)
计量
- 文章访问数: 565
- HTML全文浏览量: 276
- PDF下载量: 21
- 被引次数: 0