GNSS/INS Based Risk Assessment in Train Localization
-
摘要: 全球卫星导航系统（global navigation satellite system，GNSS）应用于列车运行控制系统位置服务时，需对其进行风险评估，以确保其满足安全相关的需求. 为此，首先建立一种基于卫星导航系统与惯导系统（inertial navigation system，INS）融合的列车定位单元结构，通过分析传感器融合数据对故障进行检测及识别，并计算水平保护距离，结合水平位置误差、水平告警门限、告警时间等指标参数，对列车定位单元的工作状态进行识别；其次在此基础上分析由危险状态生成的风险事件，并计算列车定位单元危险侧失效率及故障概率；最后结合现场试验数据对所提出的风险评估方法进行测试验证. 验证结果表明：若误警率、漏检率均为1 × 10−7/h，水平告警门限为20 m，定位单元在相对开阔环境下的故障率为9.14 × 10−7/h，受限环境下的故障率为1.52 × 10−4/h；若运行线路对风险指标参数需求降低，则误警率、漏检率及水平告警门限也会增大，受限环境下的定位单元故障率也随之降低，在误警率、漏检率均为1 × 10−5/h，水平告警门限为100 m时，计算获得的受限环境下定位单元故障率为0. 因此，在对定位单元进行风险评估时需考虑不同线路对指标参数的需求.Abstract: Risk assessment of global navigation satellite system (GNSS) used in train localization services is essential to fulfilling safety requirements. In this work, GNSS and inertial navigation system (INS) are integrated to build train localization units. The fault detection and identification is realized by the analysis of sensor fusion data, and the horizontal protect level (HPL) is calculated. According to horizontal position error (HPE), horizontal alert limit (HAL) and time to alert (TTA), the states of a train localization unit can be identified. Then the hazardous events caused by risky states are analyzed, the probability of wrong-side failure and the hazard rate are calculated. Finally, the risk assessment method is tested with field data. It is shown that when the false alarm rate and miss detection rate are 1 × 10−7/h, and the HAL is 20 m, the hazard rate of the train localization unit are calculated as 9.14 × 10−7/h in open area and 1.52 × 10−4 /h in constrained environment, respectively. When the railway line requirements on the risk indexes become low, i.e., the false alarm rate, miss detection rate and HAL are all increased, the hazard rate will be reduced. As a result, the hazard rate will be 0 in constrained environment when the false alarm rate and miss detection rate are all 1 × 10−5/h, and HAL is 100 m. Therefore, it is necessary to cosider requirement difference for railway lines when implementing the risk assessment.
-
图 1 基于EKF的GNSS/INS的紧耦合定位结构
Figure 1. GNSS/INS tight-coupled integration localization architecture based on EKF
表 1 精度及完好性分析相关指标
Table 1. Relevant indicators in analysis of accuracy and integrity
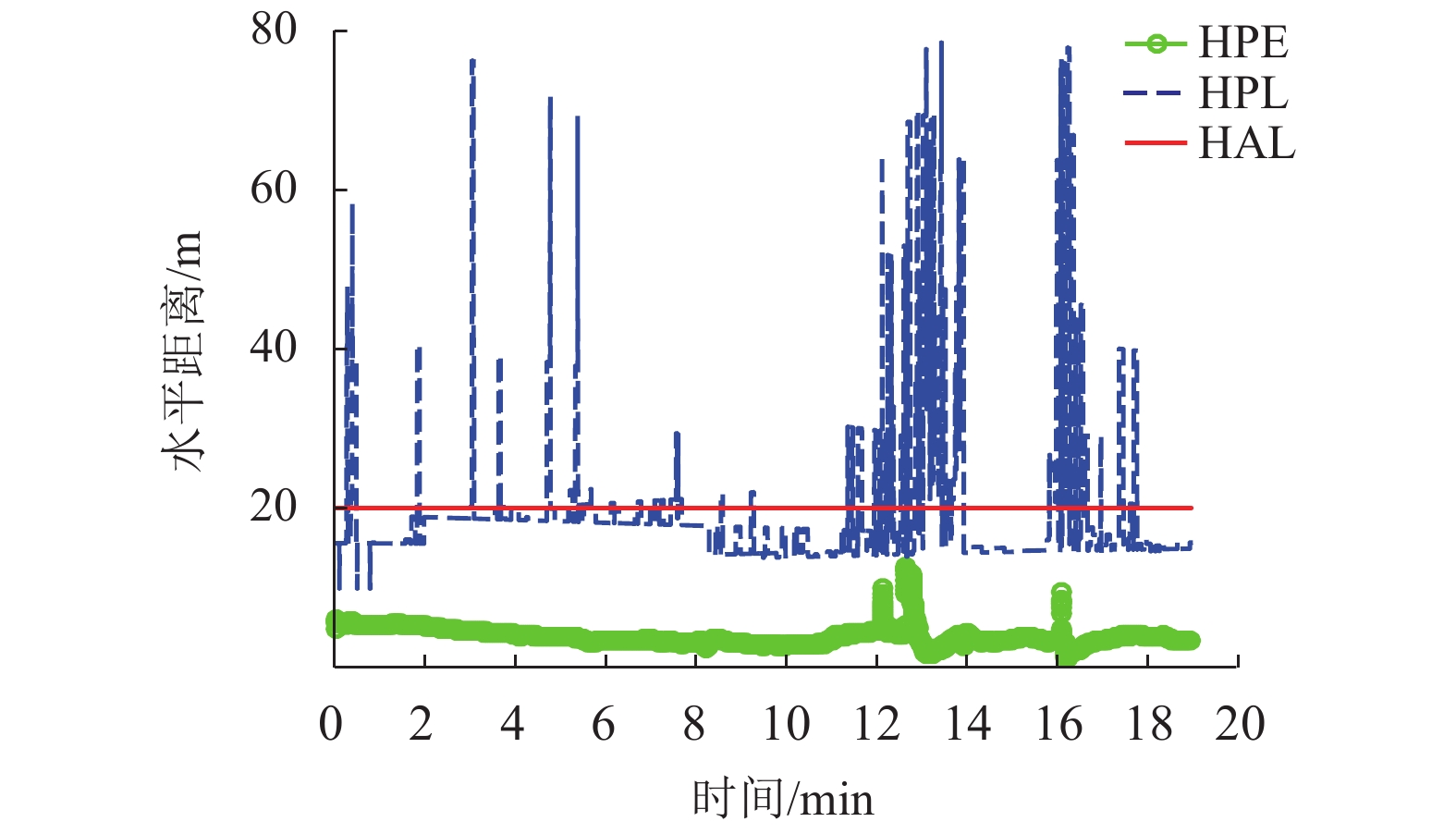
指标 缩写 量纲 符号 水平位置误差 HPE 距离 DHPE 水平保护距离 HPL 距离 DHPL 水平告警门限 HAL 距离 DHAL 告警时间 TTA 时间 TTTA 
下载: 导出CSV
表 2 试验数据参数设置
Table 2. Setting of parameters in test
指标 取值 Pfa/h−1 1 × 10−7 Pmd/h−1 1 × 10−7 HAL/m 20
下载: 导出CSV
表 3 测试数据统计
Table 3. Statistical results of test data
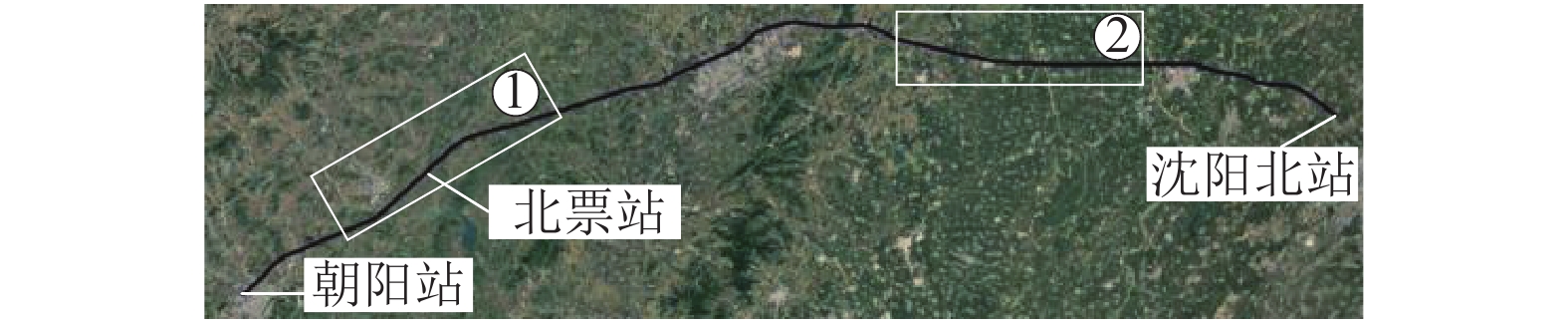
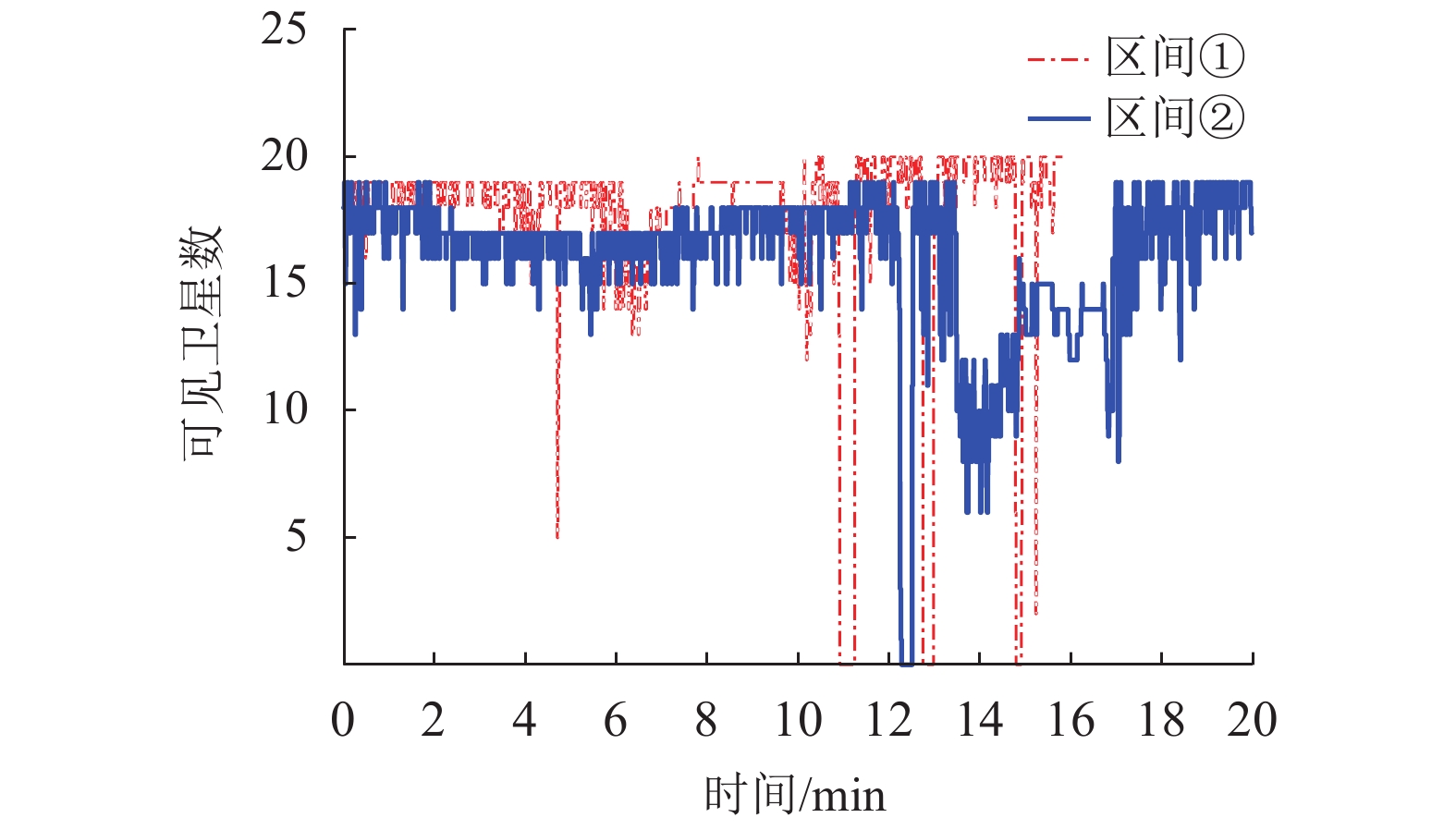
测试数据 区间① 区间② 单次平均时长/min 15.81 19.32 单次平均数据量/个 8996 11802 测试数/次 24 24 总时长/min 379.47 463.72 总数据量/个 215904 283248 检测故障数/次 152 178 状态NO数量/次 9262 1928
下载: 导出CSV
表 4 不同区间的风险评估结果
Table 4. Risk assessment results in different sections
区间 rt 发生数/次 NA/次 pwsf 故障率/h−1 区间① 13235 207 9.59 × 10−4 1.52 × 10−4 区间② 2376 2 7.06 × 10−6 9.14 × 10−7
下载: 导出CSV
表 5 不同参数下的风险评估结果
Table 5. Risk assessment results with different parameters
HAL/m Pfa/h−1 Pmd/h−1 故障率/h−1 仅考虑状态DU的故障
率/h−120 1 × 10−7 1 × 10−7 1.52 × 10−4 9.01 × 10−5 25 1 × 10−7 1 × 10−7 1.11 × 10−4 7.10 × 10−5 50 1 × 10−6 1 × 10−6 1.53 × 10−5 5.12 × 10−6 100 1 × 10−5 1 × 10−5 0 0
下载: 导出CSV
-
DORIDES C. GNSS market report 2017-rail [EB/OL]. [2019-06-20]. https://www.gsa.europa.eu/system/files/reports/gnss_market_report_2017_-_rail.pdf. 刘江,蔡伯根,王剑. 基于卫星导航系统的列车定位技术现状与发展[J]. 中南大学学报(自然科学版),2014,45(11): 4033-4042.LIU Jiang, CAI Baigen, WANG Jian. Status and development of satellite navigation system based train positioning technology[J]. Journal of Central South University (Science and Technology), 2014, 45(11): 4033-4042. FILIP A. Efficient use of multi-constellation EGNOS for the European train control system[C]//Proceedings of the 2016 European Navigation Conference (ENC GNSS 2016), Helsinki: IEEE AESS, 2016: 1-9. NGUYEN T P K, BEUGIN J, MARAIS J. Method for fvaluating an extended fault tree to analyse the dependability of complex systems:application to a satellite-based railway system[J]. Reliability Engineering & System Safety, 2015, 133: 300-313. 王剑,陆德彪,唐一哲,等. 基于虚拟应答器的GNSS列车安全定位及风险分析[J]. 铁道学报,2016,38(6): 53-58. doi: 10.3969/j.issn.1001-8360.2016.06.010WANG Jian, LU Debiao, TANG Yizhe, et al. Virtual balise application for GNSS train safe location and risk analysis[J]. Journal of the Chine Railway Society, 2016, 38(6): 53-58. doi: 10.3969/j.issn.1001-8360.2016.06.010 杨扬. 基于GNSS的列车定位系统安全风险分析研究[D]. 兰州: 兰州交通大学, 2018. LU D, SCHNIEDER E. Performance evaluation of GNSS for train localization[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(2): 1054-1059. FILIP A, BEUGIN J, MARAIS J, et al. Interpretation of the Galileo safety-of-life service by means of railway RAMS terminology[J]. Transactions on Transport Sciences, 2008, 1(2): 61-68. doi: 10.5507/tots.2008.009 LEGRAND C, BEUGIN J, MARAIS J, et al. From extended integrity monitoring to the safety evaluation of satellite-based localization system[J]. Reliability Engineering & System Safety, 2016, 155: 105-114. RUSTAMOV B, HASHIMOV A M. Multifunctional operation and application of GPS[M]. London: IntechOpen, 2018: 23-43. TORO F G, LU D, MANZ H, et al. Accuracy evaluation of GNSS for a precise vehicle control[J]. IFAC Proceedings Volumes, 2012, 45(24): 78-82. doi: 10.3182/20120912-3-BG-2031.00015 铁道部科学技术司. C3-BZ-001: CTCS-3级列控系统总体技术方案[S]. 北京: 中华人民共和国铁道部, 2008. MATTIS J N, CHAO E L, DUKE E C. 2017 federal radio navigation plan[R]. Washington: United States Department of Transportation, 2017. MOCEK H, FILIP A, BAZANT L. Galileo safety-of-life service utilization for railway non-safety and safety critical applications[J]. Journal of Mechanical Systems for Transportation and Logistics, 2010, 3(1): 119-130. doi: 10.1299/jmtl.3.119 FILIP A. The multi-constellation SBAS-R interface as an international standard for high-safety integrity land transport systems[C]//2015 25th International Conference Radioelektronika (RADIOELEKTRONIKA). [S.l.]: IEEE, 2015: 203-208. European GNSS Agency. Rail report on user needs and requirements v1.0[EB/OL]. [2019-06-20]. https://www.gsc-europa.eu/sites/default/files/sites/all/files/Report_on_User_Needs_and_Requirements_Rail.pdf -
下载:
点击查看大图
图(8) / 表(5)
计量
- 文章访问数: 665
- HTML全文浏览量: 417
- PDF下载量: 24
- 被引次数: 0