Experimental Study on Deformation Behavior of Polypropylene Fiber Reinforced Concrete Beams
-
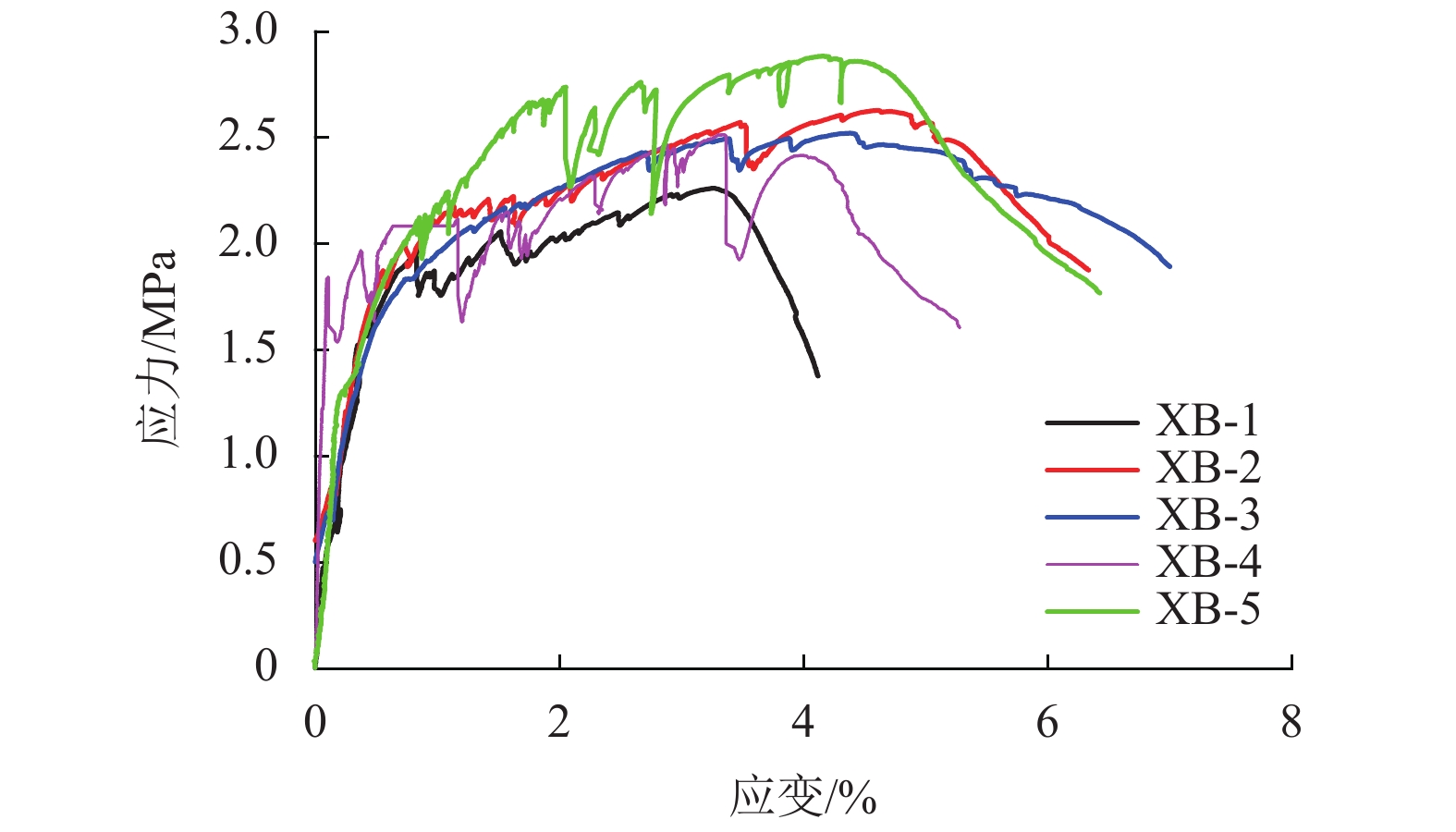
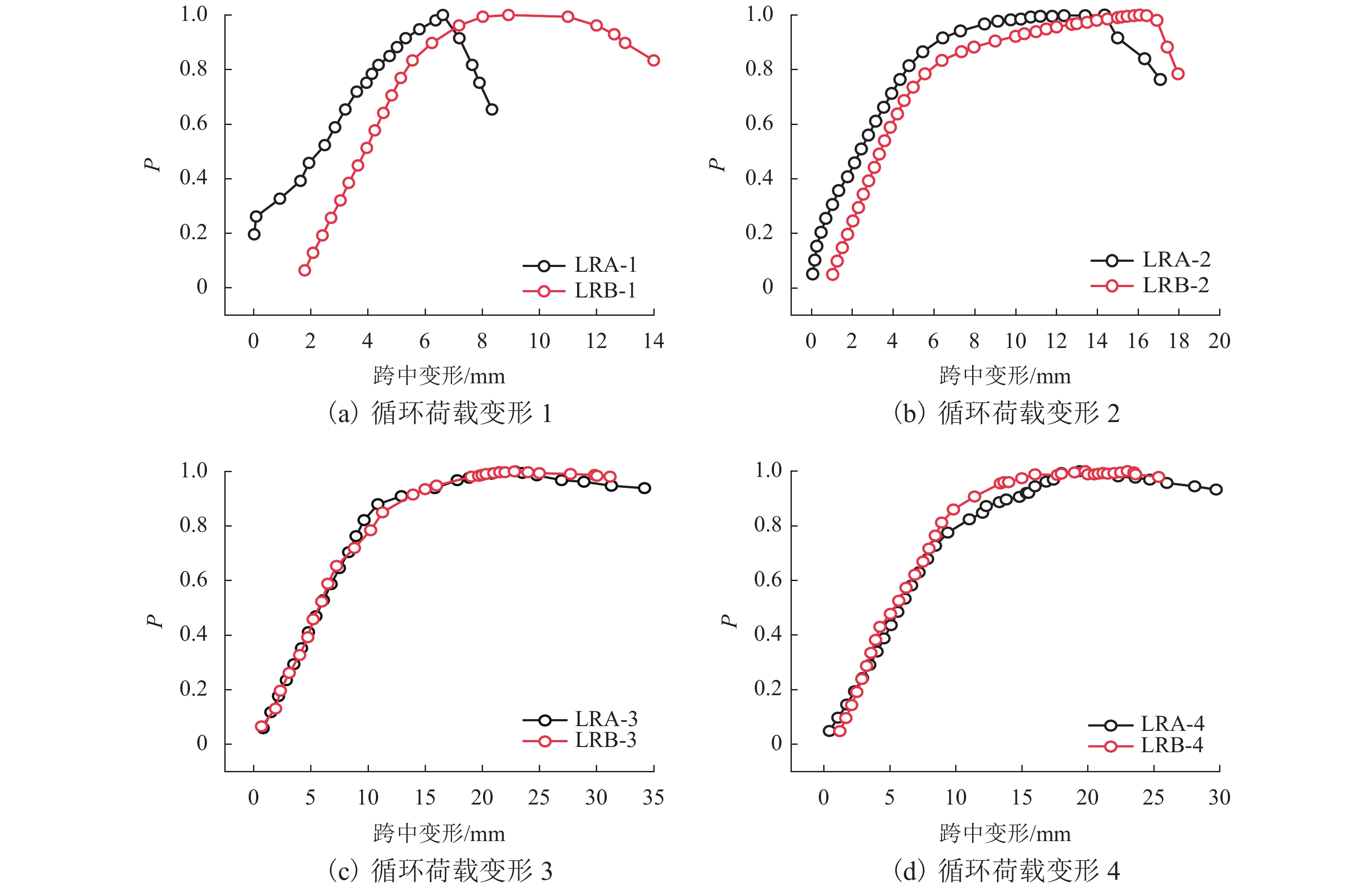
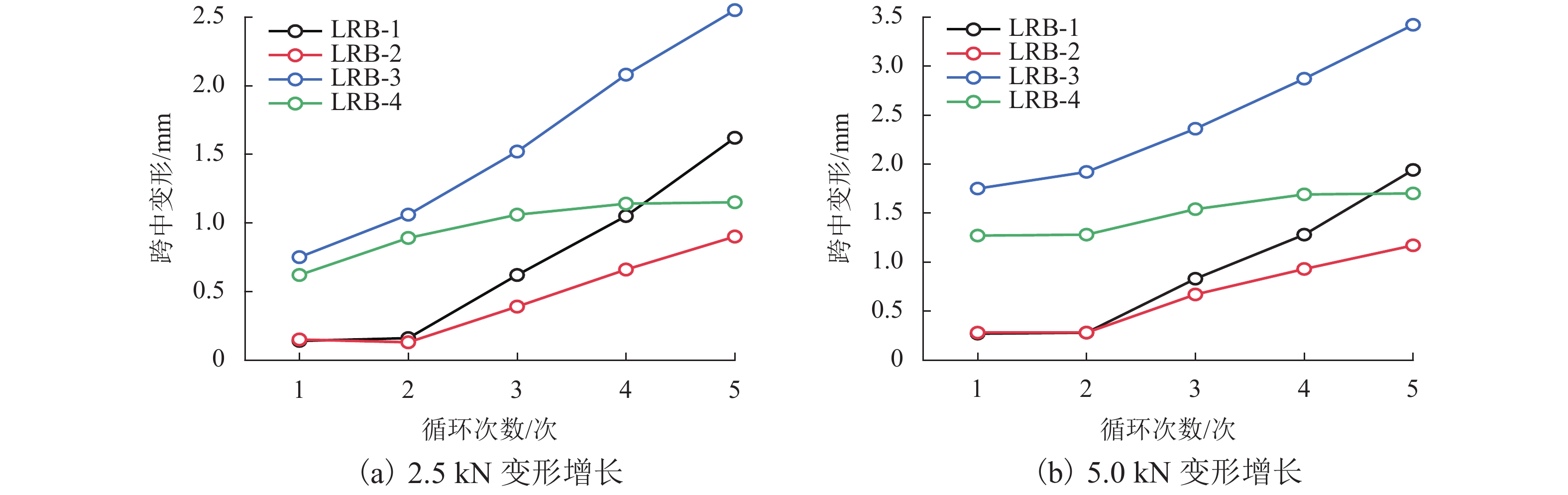
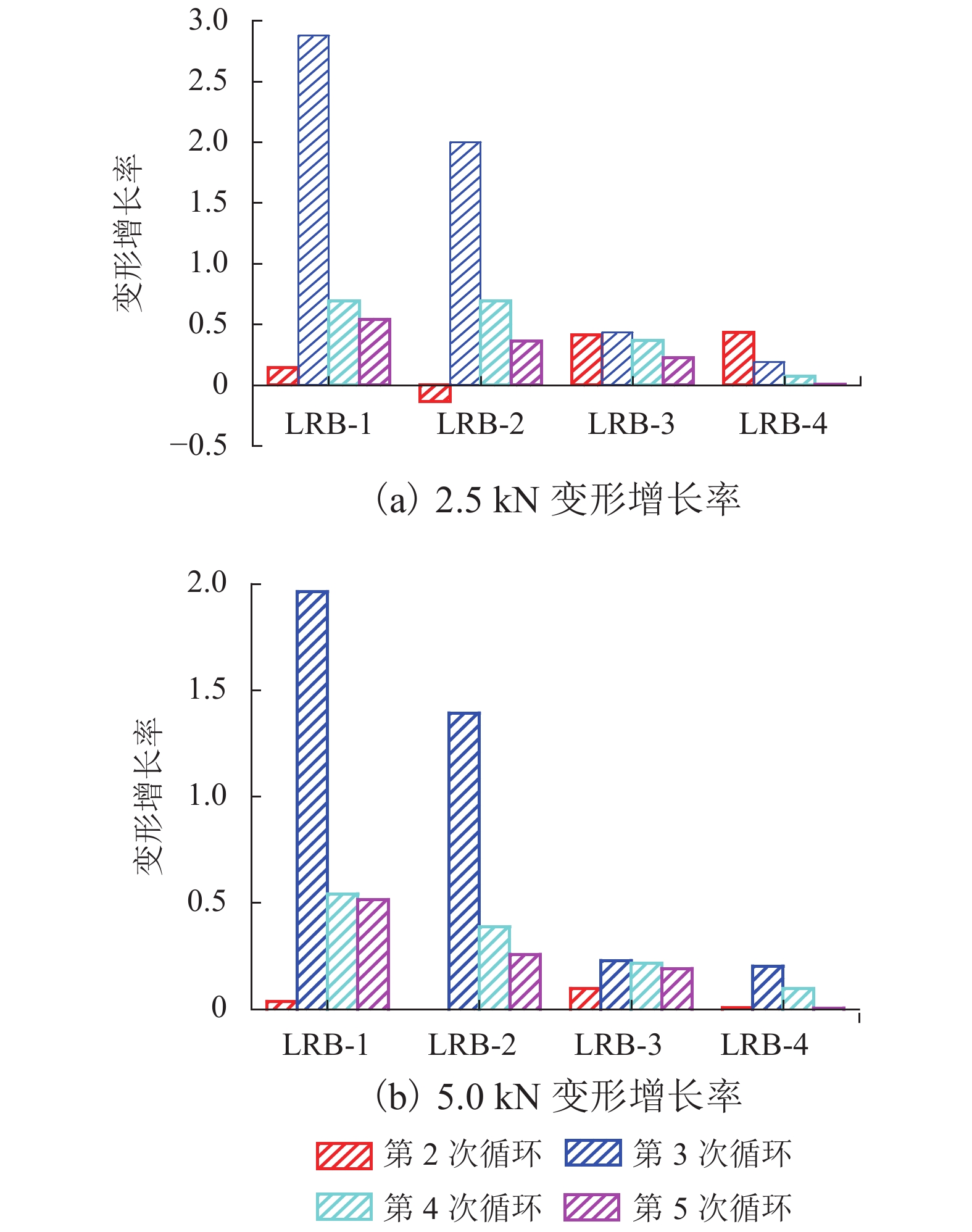
摘要: 为探究PP-ECC梁与RC梁变形发展规律的区别，通过逐级加载和循环加载两种加载制度对4根PP-ECC梁和4根RC梁进行抗弯试验；同时，基于有效惯性矩法推导出适用于短期荷载作用下PP-ECC梁的最大变形计算公式. 研究结果表明：逐级加载下，PP-ECC梁呈现出更为明显的塑性变形阶段，与RC梁相比，PP-ECC梁经过5次循环加载后的循环荷载变形曲线与原曲线拟合度较好；循环加载过程中，PP-ECC梁在基准荷载下的加载变形增长率和卸载变形增长率均小于相同配筋率的RC梁，呈现出更好的抗损伤变形能力和变形恢复能力；基于有效惯性矩法推导出的变形修正模型计算结果与试验结果拟合度较好，可应用于实际工程对PP-ECC梁在短期荷载作用下最大变形的计算.Abstract: In order to explore the difference in deformation behaviors of polypropylene engineered cementitious composite (PP-ECC) beam and reinforced concrete (RC) beam, bending resistance tests were performed on four PP-ECC beams and four RC beams using two loading systems, i.e., step loading and cyclic loading. Meanwhile, based on the effective moment of inertia method, the maximum deformation calculation formula applicable to the PP-ECC beams under short-term loads was derived. The results show that the PP-ECC beam undergoes a more obvious plastic deformation stage under successive loading. Compared with the RC beam, the deformation curve of the PP-ECC beam after 5 cycles of cyclic loading fits better with the original curve. During cyclic loading, the growth rates of the loading and unloading deformation of PP-ECC beams under the reference load are both lower than those of RC beams with the same reinforcement ratio, showing better damage resistance and deformation recovery ability. In general, the calculated results of deformation correction model based on the effective moment of inertia method fit well with the test results, and the proposed method can be applied to the calculation of maximum deformation of PP-ECC beams under short-term load in practical engineering.
-
高速列车的行驶引起了许多空气动力学问题，其中列车行驶过程产生的脉动风压所带来的问题受到广泛关注. 脉动风压产生于列车在高速行驶下对其周围的空气所产生的强烈扰动，当行驶的列车通过声屏障时，这一扰动将会加剧，使周围的空气产生的空气压力发生突变，形成一种瞬态的冲击压力，在很短的时间内(约几十毫秒)相继出现正、负压力峰值，这种瞬态压力冲击即为列车驶过声屏障时产生的压力波，即称为脉动风压. 刘海涛[1]曾对比分析得到了不同桥宽、不同车型、不同速度下脉动风压的分布规律，这种压力波的存在实际会对声屏障结构产生巨大影响，如果不加以重视，会引起声屏障许多结构问题和疲劳问题，很多学者都曾针对脉动风压开展了相关研究. 声屏障风荷载体型系数上，刘磊等[2]通过缩尺风洞实验，确定了声屏障迎风面净体型系数超过1.40，背风面体型系数接近0.30. 郑史雄等[3]建议桥梁声屏障的风荷载体型系数取1.65，路基声屏障的风荷载体型系数取1.99. 声屏障脉动风压响应上，焦长洲等[4]对脉动风压导致的声屏障结构振动进行了研究. 邓跞等[5]研究了金属立柱插板式声屏障在脉动风压静态作用下的静力响应. 刘功玉[6]研究了不同车速下声屏障结构在脉动风压作用下动力响应规律，发现随着车速的提高，列车经过声屏障区域时的气动压力和气动吸力也越来越大. 康健[7]研究了不同中心距的声屏障结构在列车速度为350 km/h时产生的脉动风压作用下疲劳性能规律. 张田等[8]发现防风板的应力远高于立柱的应力，疲劳问题也更为显著. 马驰[9]研究了货运铁路大型全封闭声屏障结构，发现较大的疲劳荷载作用下声屏障柱脚螺栓会发生轻微松动，在设计过程中可以严格控制拧紧力矩防止螺栓松动发生，并定期对螺栓进行检查. 结构优化方面，申真真[10]研究了不同的单元壁厚度和材料的高速铁路插板式冷弯声屏障的静动力响应及疲劳性能规律，提出了一种综合效益突出的结构组合. 赵允刚等[11]针对采用声屏障时高速列车运行过程中表面气动阻力较大的问题，提出利用减载式声屏障降低列车运行过程中受到的气动阻力. 苏卫青[12]研究了高速铁路声源特性、作用于高速铁路声屏障的气动压力和声屏障结构的动力响应. 针对前述的研究，发现目前针对不同顶部开口长度的双侧封闭式声屏障和不同顶部覆盖长度的单侧封闭式声屏障在脉动风压作用下的结构响应和疲劳性能规律的研究较少，事实上，顶部结构变化对列车行驶过程中气流的释放和结构优化有一定的意义. 本文研究不同顶部开口长度的双侧封闭式声屏障和不同顶部覆盖长度的单侧封闭式声屏障受力特征规律，并探究声屏障的关键连接部位耐久性、疲劳特性，为高铁桥上半封闭式声屏障的设计提供有力的技术支持.
1. 工程概况
某高铁声屏障结构采用单双侧封闭直立型金属插板式声屏障形式，列车运行车速为350 km/h，金属插板式声屏障主要由 H 型钢立柱、H 型钢底板、铝合金单元板、橡胶等结构组成，钢架部分采用Q345- B焊接工字钢；铝合金单元板采用标号不低于5A03、厚度不小于1.5 mm的铝合金材料，面板和背板需进行铬酸钝化或类似的预处理；通透吸声板采用厚度不小于20.0 mm的透明板，具有防撞击、防破损保护措施及防鸟撞击标志. 单元板及透明板四面加设铝合金框，铝合金框与型钢立柱间采用插入式柔性连接[11].
声屏障结构截面沿顶部直线段分割情况及列车所在位置（图示右轨道）共分为3部分：近轨竖直声屏障部分、远轨竖直声屏障部分及顶部横向声屏障部分. 声屏障结构截面示意如图1所示.
2. 模型建立过程
本文探讨双侧封闭声屏障顶部开口间距为（即顶部不设置通透隔声板和吸声板）2、4、6、8 m以及单侧封闭式声屏障顶部覆盖长度为（即顶部设置通透隔声板）2、4、6、8 m 8种情况下声屏障结构的受力特征. 工况参数如表1所示.
表 1 工况参数Table 1. Operating parameters工况参数名称 取值 车型 CRH3 列车速度/(km•h−1) 350 双侧封闭式声屏障顶部
开口间距/m2、 4、 6、 8 单侧封闭式声屏障顶部
覆盖长度/m2、 4、 6、 8 2.1 脉动风压时程函数提取
本文脉动风压计算及结果参照李小珍等[13-14]的脉动风压的CFD （computation fluid dynamics）模型，该模型为行进中的高速铁路半封闭声屏障的列车通过开口间距双侧封闭声屏障和顶部不同的覆盖长度单侧封闭声屏障产生的. 用动态铺层技术模拟移动列车表面流场，动网格部分模拟了高速列车表层及列车周围因列车高速前进，受列车移动影响最大的空气，模型如图2所示. 在此CFD模型中，近轨竖直声屏障部分分为17个区域，自下到上分别用N1～N17标记测点；远轨竖直声屏障部分设置17个区域，自下到上分别用F1～F17标记测点（单侧封闭式声屏障不布置）；顶部横向声屏障部分根据顶部开口间距的不同区域有所变化，靠近轨一侧由近轨至开口处用T1～T10标记测点，靠远轨用T15～T24标记测点，开口间距每增加2 m，顶部两侧测点从大序号依次各减少两个. 测点的整体布置 （双侧封闭式声屏障顶部开口间距2 m和单侧封闭式声屏障顶部覆盖长度8 m） 如图3.
一趟CRH3完整驶过后，记录各个测点随时间变化的受力情况，得到脉动风压作用的时程曲线，梳理罗云柯[14]模型数据结果，以双侧封闭式顶部开口2 m模型为例，声屏障近轨、远轨、顶部风压时程函数如图4，结果用于整体模型动力计算.
考虑最不利的静力风压情况，提取其中风压极值计算结果如图5，结果用于整体模型静力计算.
图 4 双侧封闭式声屏障顶部开口间距2 m模型脉动风压时程函数Figure 4. Time histories of pulsating wind pressure on the double-side closed sound barrier model with 2 m top opening spacing2.2 整体模型建立
得到脉动风压的时程曲线后，利用midas civil有限元软件分别建立了顶部不同的开口间距双侧封闭式声屏障及顶部不同覆盖长度的单侧封闭式声屏障整体模型，用于分析自然风、静力风压和脉动风压分别作用下，声屏障立柱顶部位移、立柱根部弯矩、轴力及应力计算结果，并计算动力放大系数.
模型共截取10个声屏障节段，声屏障结构共计长度20 m，宽度间距12 m，高度7.75 m. 梁体材料选用C30，采用梁单元模拟；声屏障立柱材料选用Q345钢，采用梁单元模拟；声屏障铝合金复合吸声板及通透吸声板根据实际设计参数进行材料拟定，材料性能指标见表2和表3，采用板单元模拟.
表 2 铝合金复合吸声板的性能指标Table 2. Performance indexes of aluminum alloy composite sound absorption board指标名称 性能指标 降噪系数 ≥ 0.7 隔声量 ≥ 25 dB 面密度 ≤ 40 kg/m2，且≥ 20 kg/m2 抗风压性能 ≥ 8.0 kPa 抗冲击 符合《铁路声屏障声学构件技术要求和测试方法》（TB/T 3122—2010） 抗火性能 防火等级应满足《建筑材料及制品燃烧性能分级》（GB 8624—2012）规定的 B1 级及以上 防腐蚀 声屏障声学构件的金属部件的防腐蚀年限应 ≥ 25 a 抗变形性能 符合《铁路声屏障声学构件技术要求和测试方法》（TB/T 3122—2010）最大弹性挠度 ≤ L/100 耐候性能 符合《铁路声屏障声学构件技术要求和测试方法》（TB/T 3122—2010） 使用年限 ≥ 25 a 表 3 通透隔声板的性能指标Table 3. Performance indexes of transparent sound insulation board指标名称 性能指标 隔声量 ≥ 25 dB 密度 ≤ 1 200 kg/m3 透光率 透光率不应小于 90%，10 年内透光率下降为 10% 拉伸强度 ≥ 70 MPa 弯曲强度 ≥ 98 MPa 弹性模量 ≥ 3 100 MPa 断裂伸长率 ≥ 4% 防火性能 复合《建筑材料的燃烧等级分级》（GB 8624—2012）规定的 B1 级及以上 0～50 ℃ 以内线性热膨胀系数 ≤ 0.000 07 允许最高长期使用温度 ≤ 70 ℃ 软化温度 ≥ 110 ℃ 抗冲击 符合《铁路声屏障声学构件技术要求和测试方法》（TB/T 3122—2010） 板厚 ≥ 20 mm 使用年限 ≥ 25 a 
图 6 不同顶部开口间距的双侧封闭式声屏障整体模型Figure 6. Global model of the double-side closed sound barrier with different top opening spacings
图 7 不同顶部覆盖长度的单侧封闭式声屏障整体模型Figure 7. Global model of the single-side closed sound barrier with different top covering lengths结构约束关系上，立柱底部与梁体固结，立柱与声屏障板之间采用弹性约束模拟纵桥向橡胶连接作用，声屏障板与板之间释放部分端部约束模拟真实接触效果.
2.3 瑞利阻尼
振型是结构的一个重要动力特性，振型的数量和各阶振型对结构总体反应的贡献直接影响到结构地震反应的计算结果.
本文通过振型分解将多自由度体系的振动转化为单自由度体系振动的组合问题进行计算，模型结构的质量和刚度分布不均匀，振型分解反应谱法所需的振型数取振型参与质量达到总质量的90%时所需的振型数，8个模型所需振型数为93～101个. 若假设阻尼与质量矩阵和刚度矩阵的组合成比例，则可表示为
c=αm+βk， (1) 式中：
c 为阻尼矩阵；α 和β 均为与频率相关的参数；m 和k 分别为质量矩阵和刚度矩阵.这种阻尼称为瑞利阻尼. 利用瑞利阻尼法公式计算得到各阶瑞利阻尼比为
α2ω+ωβ2=ξ， (2) 式中：
ω 为模态对应频率；ξ 为阻尼比.依据钢结构抗震要求[15-16]，
ξ 取0.02，相关参数α 和β 是随频率变化的，用频率范围的下限和上限代入式（2），联立求解得到各个声屏障结构的α 和β ，结果如表4.各个声屏障结构的
α 和β 代入瑞利阻尼公式，计算得到声屏障结构各阶振型的阻尼比，用于动力计算.表 4 各个声屏障结构的α 和β Table 4. Values ofα andβ of each sound barrier structure结构形式 参数 开口间距/m 2 4 6 8 双侧封闭式
声屏障α 0.46773 0.47596 0.48947 0.50614 β 0.00063 0.00060 0.00054 0.00048 单侧封闭式
声屏障α 0.67421 0.55969 0.51430 0.42194 β 0.00034 0.00041 0.00051 0.00060 2.4 风压时程函数输入
加载原则上，静力作用时，考虑最不利的受力情况，提取各位置脉动风压的峰值，按静力方式作用于声屏障结构，得到最大静力响应结果a；动力计算采用振型叠加法，利用前述瑞利阻尼法计算所得的每一阶振型的阻尼进行动力计算，动力计算分析采用CFD，取一个荷载子步为0.005 s动力时长共30 s，按各个测点分块，按2 m一个节间，根据时程递进，将脉动风压时程曲线施加于整个声屏障结构上得到静力响应同一测点的动力响应结果b. b/a得到结构动力放大系数.
3. 计算结果
不同开口形式的声屏障结构在立柱的位移、应力、弯矩、轴向力、水平力的峰值位置基本一致，最大位移位置主要分布在近轨部分的立柱顶部；最大应力、最大弯矩位置主要分布在近轨部分的立柱底部；立柱结构最大轴力位置分布在远轨部分的立柱底部；立柱结构最大水平力位置分布在近轨部分的立柱底部，以双侧顶部开口间距2 m的双侧封闭声屏障为例，静力动力计算结果示意如图8、9.
所有声屏障结构计算结果汇总见表5.
从计算结果来看，对于双侧封闭式声屏障，随着顶部开口间距的增大，响应减小，对于开口4、6 m内力变化影响不大，开口2 m的立柱动应力是开口8 m的立柱动应力的1.15倍，放大系数相差0.12，对于单侧封闭式声屏障中，覆盖的长度增加，响应增大，覆盖长度4～6 m后有较大变化，覆盖8 m的立柱动应力是覆盖2 m的立柱动应力的1.28倍，放大系数相差0.37.
图 8 双侧封闭顶部开口间距2 m声屏障立柱静力响应结果Figure 8. Static responses of the double-side closed sound barrier columns with 2 m top opening spacing表 5 受力特征结果Table 5. Force characteristic results型式 类别 立柱底部
应力/MPa立柱顶部位移/mm 立柱弯矩/（kN•m） 轴向力/kN 水平力/kN 双侧封闭式顶部开口间距 2 m 动力作用 20.60 5.82 37.24 19.42 52.09 放大系数 2.10 3.75 2.10 3.26 1.94 静力作用 9.62 1.49 17.48 5.50 26.51 双侧封闭式顶部开口间距 4 m 动力作用 19.55 5.47 34.90 17.14 51.45 放大系数 2.03 4.08 2.00 3.14 1.83 静力作用 9.60 1.54 17.38 5.50 25.95 双侧封闭式顶部开口间距 6 m 动力作用 19.48 5.09 34.81 16.90 50.35 放大系数 2.02 3.43 2.00 3.15 1.97 静力作用 8.99 1.51 16.27 3.09 24.20 双侧封闭式顶部开口间距 8 m 动力作用 17.88 4.62 32.18 11.31 45.84 放大系数 1.98 3.75 1.97 3.73 2.01 静力作用 8.83 1.34 15.99 2.35 23.31 单侧封闭式顶部覆盖长度 2 m 动力作用 19.02 5.09 34.37 8.24 51.10 放大系数 2.15 3.80 2.15 3.50 2.19 静力作用 9.24 1.49 16.74 2.62 27.41 单侧封闭式顶部覆盖长度 4 m 动力作用 20.10 5.33 36.34 5.33 51.15 放大系数 2.18 3.61 2.17 2.03 2.00 静力作用 9.62 1.54 17.42 1.74 26.28 单侧封闭式顶部覆盖长度 6 m 动力作用 23.19 5.89 41.56 6.16 59.75 放大系数 2.41 3.41 2.39 3.54 2.01 静力作用 9.69 1.52 17.51 2.65 26.42 单侧封闭式顶部覆盖长度 8 m 动力作用 24.44 6.27 44.08 6.57 62.25 放大系数 2.52 4.13 2.52 2.48 2.36 静力作用 9.78 1.55 17.74 5.95 26.83 
图 9 双侧封闭式声屏障顶部开口间距2 m模型动力时程响应曲线结果Figure 9. Dynamic response time-histories of the double-side closed sound barrier model with 2 m top opening spacing4. 结 论
1） 立柱结构最大位移位置分布在近轨部分的立柱顶部；立柱结构最大弯矩位置分布在近轨部分的立柱底部；立柱结构最大轴力位置分布在远轨部分的立柱底部；立柱结构最大水平力位置分布在近轨部分的立柱底部；立柱结构最大应力位置分布在近轨部分的立柱底部.
2） 双侧封闭式声屏障结构中，立柱最大弯矩、最大应力和放大系数随着顶部开口间距的增加有减小的趋势；同理，单侧封闭式声屏障中，立柱最大弯矩、最大应力和动力放大系数随着顶部覆盖程长度的增加有增大的趋势.
3） 双侧封闭式声屏障中，最不利结构为顶部开口间距2 m的双侧封闭式声屏障结构，单侧封闭式声屏障中，最不利结构为顶部覆盖8 m的单侧封闭式声屏障结构. 两种结构形式不同，单侧封闭式声屏障内力变化对顶部覆盖长度更为敏感，且单侧封闭式引起的动力响应更大，可能是由于双侧封闭后，远轨侧同样受到了脉动风作用，近远轨侧脉动风的作用叠加减小了内力响应.
-
表 1 试件参数
Table 1. Sample parameters
编号 加载
方式材料 纵筋直
径/mm纵筋
型号箍筋直
径/mm箍筋
型号LRA-1 LRA C30 8 HRB400 6 Q235 LRA-2 C30 10 HRB400 6 Q235 LRA-3 PP-ECC 8 HRB400 6 Q235 LRA-4 PP-ECC 10 HRB400 6 Q235 LRB-1 LRB C30 8 HRB400 6 Q235 LRB-2 C30 10 HRB400 6 Q235 LRB-3 PP-ECC 8 HRB400 6 Q235 LRB-4 PP-ECC 10 HRB400 6 Q235 
下载: 导出CSV
表 2 PP纤维性能指标
Table 2. PP fiber performance indexes
参数 长度/
mm密度/
（kg•m−3）直径/
μm抗拉强
度/MPa弹性模
量/GPa伸长
率/%取值 12 0.91 × 103 20 480 5.00 15
下载: 导出CSV
表 3 PP-ECC性能指标
Table 3. PP-ECC performance indexes
参数 开裂抗拉强度/
MPa开裂抗拉应变/
%极限抗拉强度/
MPa极限抗拉应变/
%极限抗压强度/
MPa极限抗压应变/
%弹性
模量E/GPa取值 0.84 0.09 2.32 3.8 32.09 0.41 13.35
下载: 导出CSV
表 4 C30混凝土性能指标
Table 4. C30 concrete performance indexes
参数 抗压强度/MPa 抗压应变/% 弹性模量/GPa 取值 33.47 0.09 24.80
下载: 导出CSV
表 5 HRB400钢筋性能指标
Table 5. HRB400 steel performance indexes
参数 直径/
mm截面面
积/mm2屈服强
度/MPa极限强
度/MPa弹性模
量/GPa取值 8 50.24 406 576 197.00 10 78.50 411 535 203.00
下载: 导出CSV
表 6 卸载变形增长
Table 6. Unloading deformation growth
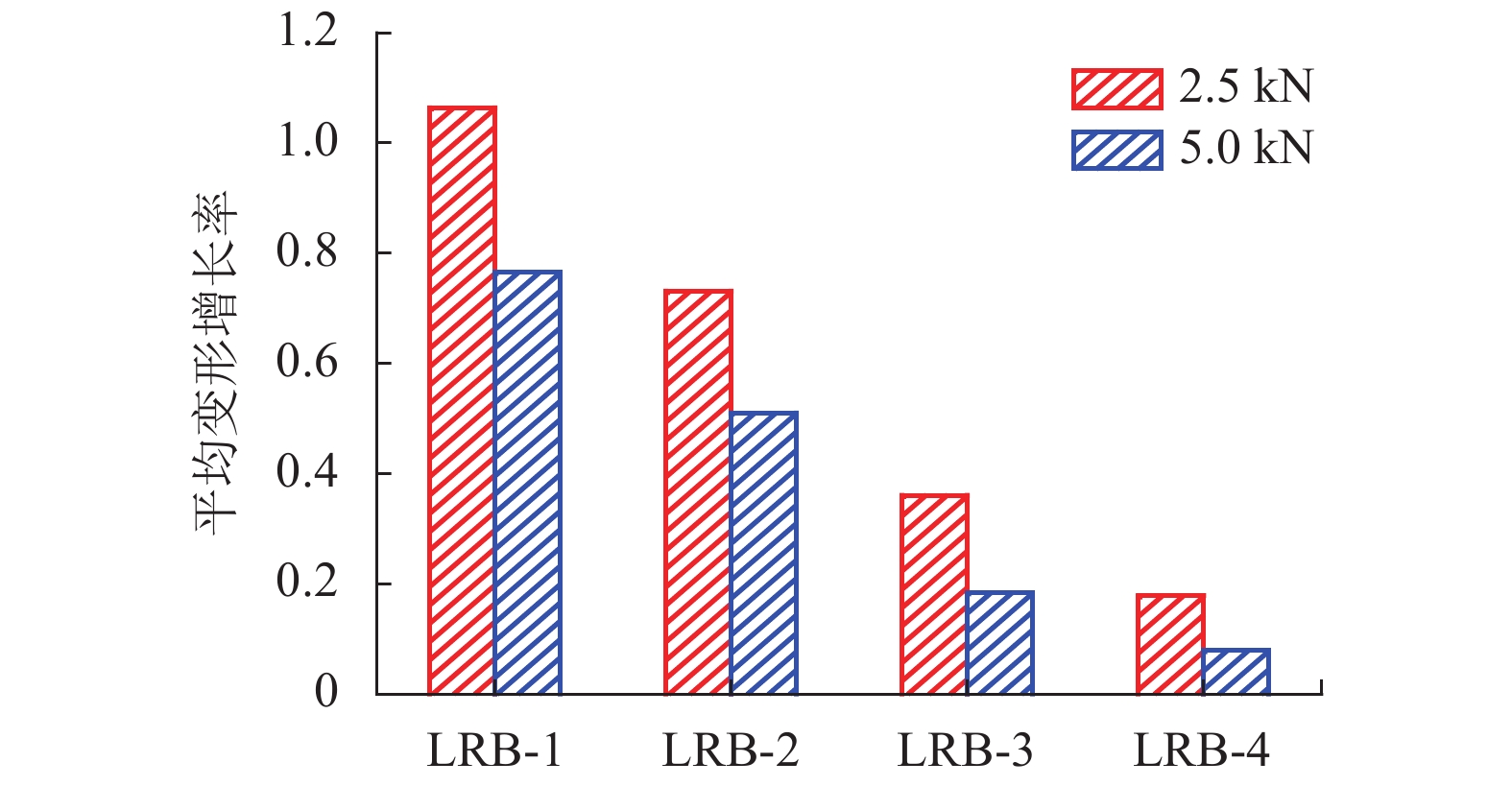
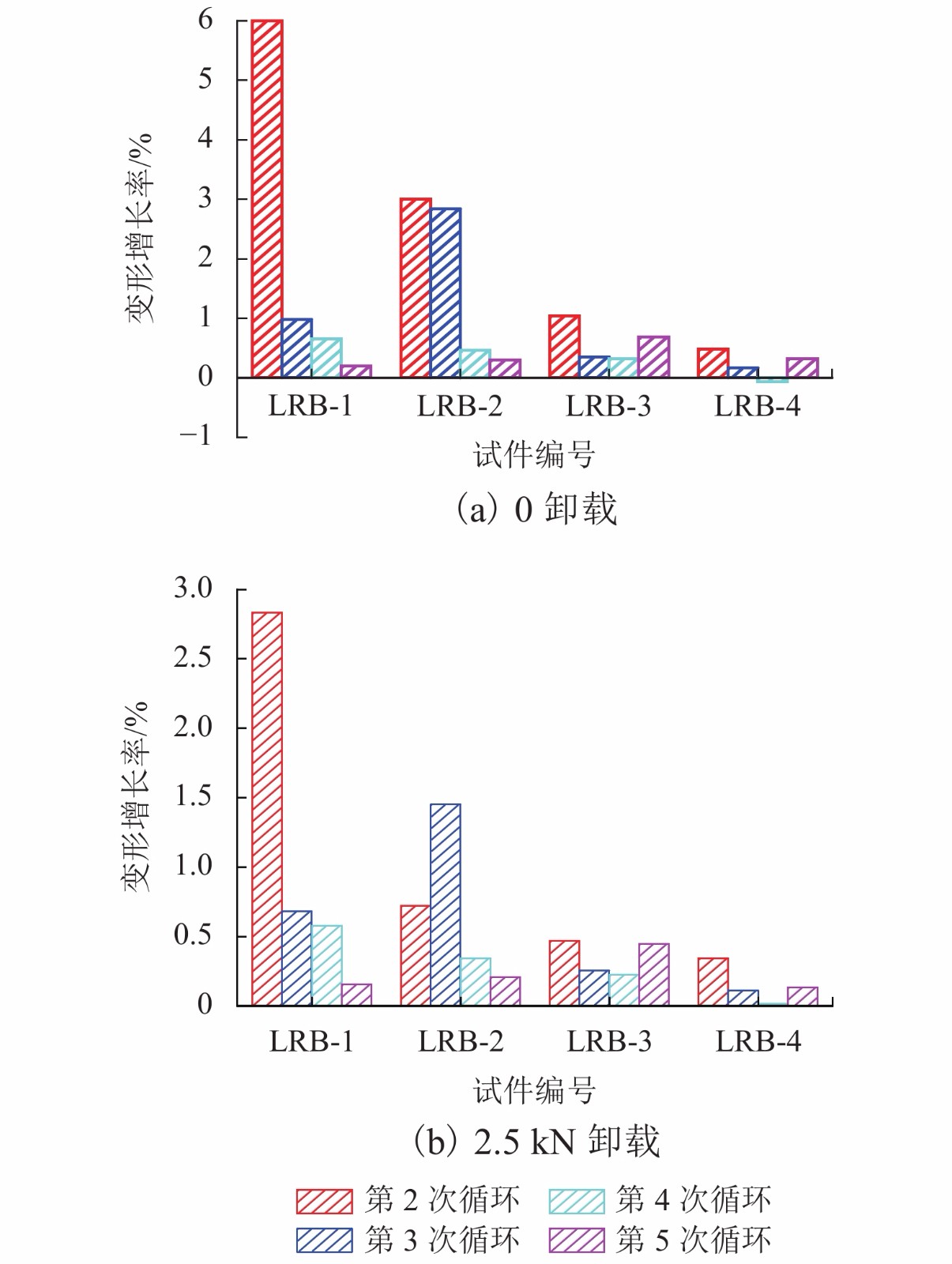
编号 平均卸载变形增长率/% 卸载变形增长方差/mm 0 2.5 kN 0 2.5 kN LRB-1 195.59 106.13 5.530 1.090 LRB-2 164.71 68.05 1.620 0.230 LRB-3 59.58 34.78 0.086 0.012 LRB-4 22.61 14.99 0.041 0.014
下载: 导出CSV
-
俞家欢. 超强韧性纤维混凝土的性能及应用[M]. 北京: 中国建筑工业出版社, 2012: 183-184. KANDA T, LI V C. New micro-mechanics design theory for pseudo strain hardening cementitious composite[J]. ASCE Journal of Engineering Mechanics, 1999, 125(4): 373-381. doi: 10.1061/(ASCE)0733-9399(1999)125:4(373) YAO Ding, YU Kequan, YU Jianggao, et al. Structural behaviors of ultra-high performance engineered cementitious composites (UHP-ECC) beams subjected to bending-experimental study[J]. Construction and Building Materials, 2018, 177: 102-115. doi: 10.1016/j.conbuildmat.2018.05.122 王玉清,刘潇,刘曙光,等. PVA-ECC徐变性能试验研究[J]. 建筑材料学报,2019,23(4): 823-830,845.WANG Yuqing, LIU Xiao, LIU Shuguang, et al. Experimental study on creep behaviors of PVA-ECC[J]. Journal of Building Materials, 2019, 23(4): 823-830,845. MENG D, LEE C K. Flexural and shear behaviours of plain and reinforced polyvinyl alcohol-engineered cementitious composite beams[J]. Engineering Structures, 2017, 151: 261-272. doi: 10.1016/j.engstruct.2017.08.036 HOSSAIN K M A, ALAM S, ANWAR M S, et al. High performance composite slabs with profiled steel deck and engineered cementitious composites-strength and shear bond characteristics[J]. Construction and Building Materials, 2016, 125: 227-240. doi: 10.1016/j.conbuildmat.2016.08.021 CAI Jingming, PAN Jinlong, ZHOU Xiangming, et al. Flexural behavior of basalt FRP reinforced ECC and concrete beams[J]. Construction and Building Materials, 2017, 142: 423-430. doi: 10.1016/j.conbuildmat.2017.03.087 CHEN Y, YU J, LEUNG C K Y. Use of high strength strain-hardening cementitious composites for flexural repair of concrete structures with significant steel corrosion[J]. Construction and Building Materials, 2018, 167: 325-337. doi: 10.1016/j.conbuildmat.2018.02.009 MOHAMMAD M R, LEE C K, SAFAT A, et al. Flexural behaviour of steel composite beams encased by engineered cementitious composites[J]. Journal of Constructional Steel Research, 2018, 143: 279-290. doi: 10.1016/j.jcsr.2018.01.004 IEVA P, GREGOR F. Phenomenological interpretation of the shear behavior of reinforced engineered cementitious composite beams[J]. Cement and Concrete Composites, 2016, 73: 213-225. doi: 10.1016/j.cemconcomp.2016.07.018 俞家欢,邹静辉. FRP筋增强PP-ECC梁滞回性能试验研究[J]. 土木工程学报,2012,45(增刊2): 84-88.YU Jiahuan, ZOU Jinghui. Experimental study on FRP reinforced PPECC beams under reverse cyclic loading[J]. China Civil Engineering Journal, 2012, 45(S2): 84-88. 袁方,陈梦成,王文波. 往复荷载下钢筋增强ECC梁的抗剪性能研究[J]. 铁道学报,2018,40(8): 146-153. doi: 10.3969/j.issn.1001-8360.2018.08.019YUAN Fang, CHEN Mengcheng, WANG Wenbo. Study on shear behavior of steel reinforced ECC beams under reversed cyclic loading[J]. Journal of the China Railway Society, 2018, 40(8): 146-153. doi: 10.3969/j.issn.1001-8360.2018.08.019 樊健生,施正捷. 钢-ECC组合梁负弯矩受弯性能试验研究[J]. 土木工程学报,2017,50(4): 64-72.FAN Jiansheng, SHI Zhengjie. Experimental research on negative bending behavior of steel-ECC composite beams[J]. China Civil Engineering Journal, 2017, 50(4): 64-72. WEN J G, ASHRAF F A, YU J M, et al. Flexural behaviors of ECC-concrete composite reinforced with steel bars[J]. Construction and Building Materials, 2018, 159: 175-188. doi: 10.1016/j.conbuildmat.2017.10.101 QUDAH S, MAALEJ M. Application of engineered cementitious composites (ECC) in interior beam-column connections for enhanced seismic resistance[J]. Engineering Structure, 2014, 69: 235-245. doi: 10.1016/j.engstruct.2014.03.026 ELGAWADY M A, DAWOOD H M. Analysis of segmental piers consisted of concrete filled FRP tubes[J]. Engineering Structure, 2012, 38: 142-152. doi: 10.1016/j.engstruct.2012.01.001 李福海,胡丁涵,余泳江,等. PP-ECC梁抗弯性能试验研究[J]. 西南交通大学学报,2019,54(2): 272-281.LI Fuhai, HU Dinghan, YU Yongjiang, et al. Experimental study on flexural capacity of PP-ECC beam[J]. Journal of Southwest Jiaotong University, 2019, 54(2): 272-281. 贾毅,赵人达,占玉林,等. PP-ECC用于墩底塑性铰区域的抗震性能试验[J]. 中国公路学报,2019,32(7): 100-110.JIA Yi, ZHAO Renda, ZHAN Yulin, et al. Experimental investigation on seismic behavior of bridge piers with polypropylene-engineered cementitious composite in plastic hinge regions[J]. China Journal of Highway and Transport, 2019, 32(7): 100-110. 周双. 纤维增强水泥基复合材料试验研究及其桥梁无缝化改造中的应用[D]. 成都: 西南交通大学, 2017. 李碧雄,廖桥,章一萍,等. 超高强钢筋工程用水泥基复合材料[J]. 吉林大学学报(工学版),2019,49(4): 1153-1161.LI Bixiong, LIAO Qiao, Zhang Yiping, et al. Theoretical on flexural behavior of ultra high strength rebar reinforced engineered cementitious composites beam[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(4): 1153-1161. 陈绪军. FRP片材加固钢筋混凝土梁挠度计算方法研究[J]. 铁道学报,2017,39(11): 103-107. doi: 10.3969/j.issn.1001-8360.2017.11.016CHEN Xujun. Study on deflection calculation method for reinforced concrete beams strengthened with FRP sheets[J]. Journal of the China Railway Society, 2017, 39(11): 103-107. doi: 10.3969/j.issn.1001-8360.2017.11.016 周建民,陈硕,王晓锋,等. 高强钢筋混凝土梁短期变形计算方法研究[J]. 同济大学学报(自然科学版),2013,41(4): 503-509.ZHOU Jianmin, CHEN Shuo, WANG Xiaofeng, et al. Calculation method of short-term deformation of concrete beams with high strength steel bars[J]. Journal of Tongji University (Natural Science), 2013, 41(4): 503-509. American Concrete Institute. Building code requirements for structural concrete and commentary: ACI 318-11[S]. Detroit: ACI Committee 318, 2011. 宁喜亮. 钢筋纤维自密实混凝土梁受弯承载力与裂缝研究[D]. 大连: 大连理工大学, 2015. 期刊类型引用(2)
1. 李涛，李梓响，郑晨昱，张子凯，张利平. 求解U型拆卸线平衡问题的多目标教与学优化. 组合机床与自动化加工技术. 2025(02): 229-235 . 
百度学术2. 张雷，耿笑荣，陶凯博. 考虑碳排放与收益的随机并行拆卸线平衡优化. 机械工程学报. 2023(07): 330-338 . 百度学术其他类型引用(5)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 568
- HTML全文浏览量: 315
- PDF下载量: 12
- 被引次数: 7