Coefficient Matrix Properties of Downward Continuation for Potential Fields and Barzilai-Borwein Downward Continuation Method
-
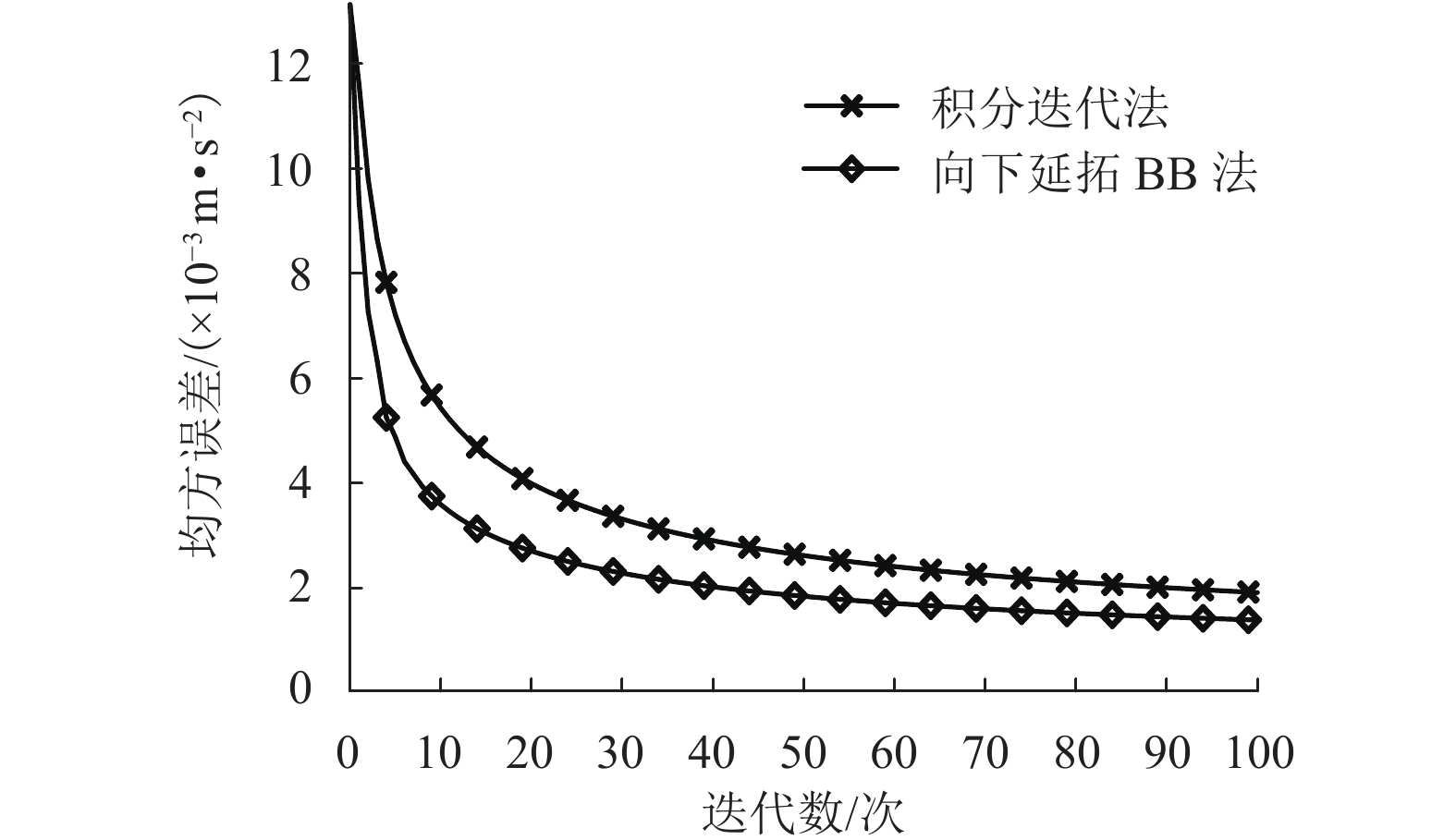
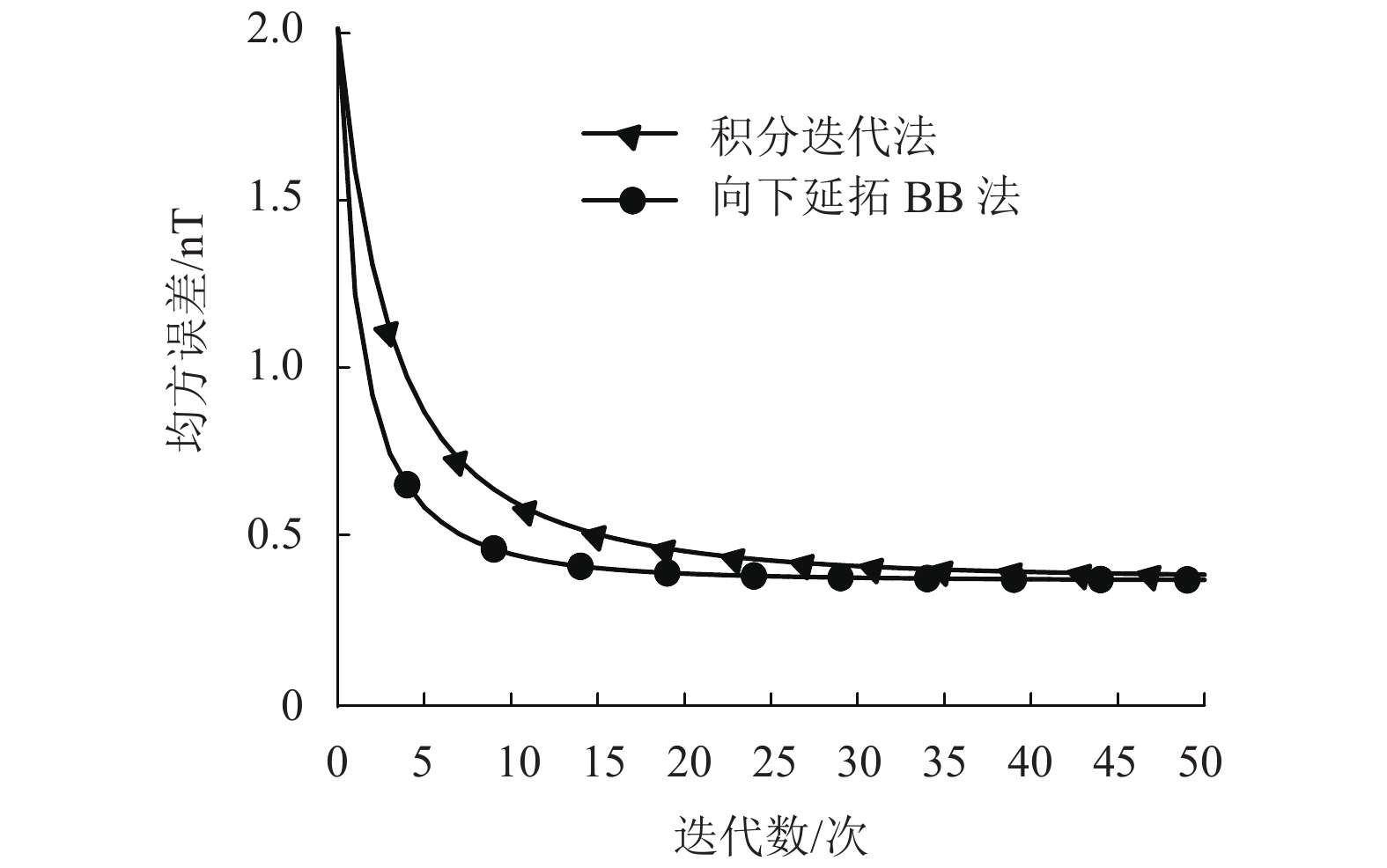
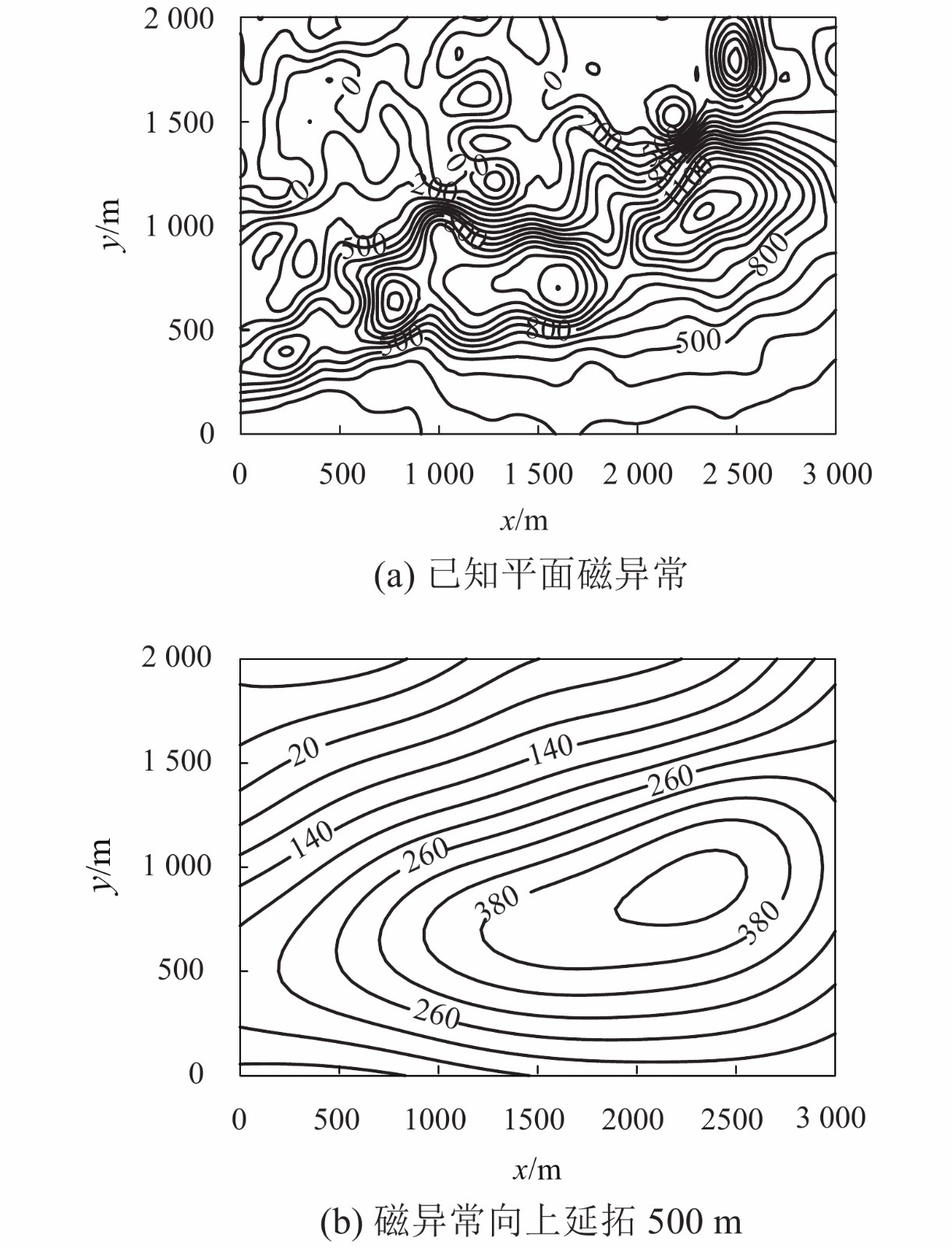
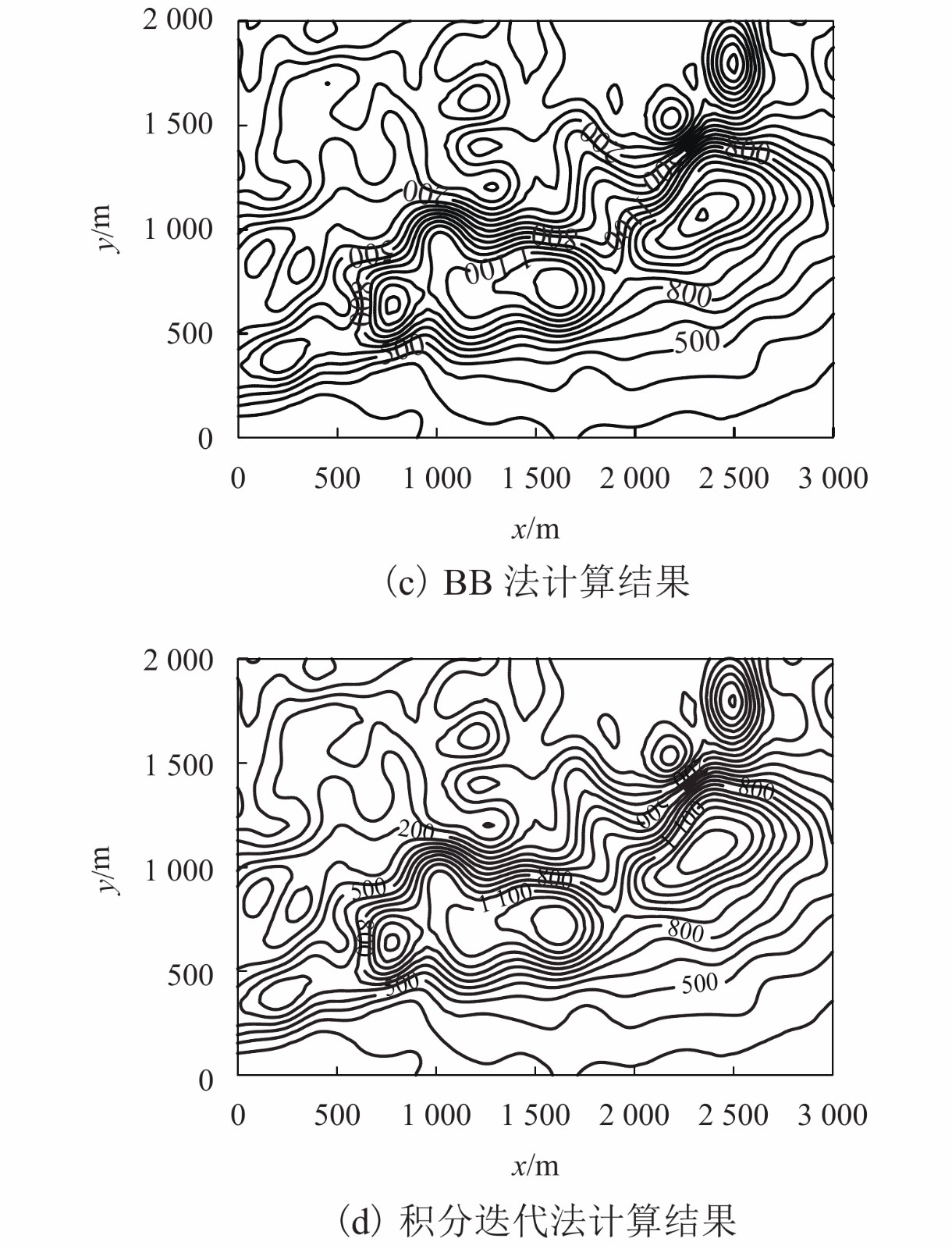
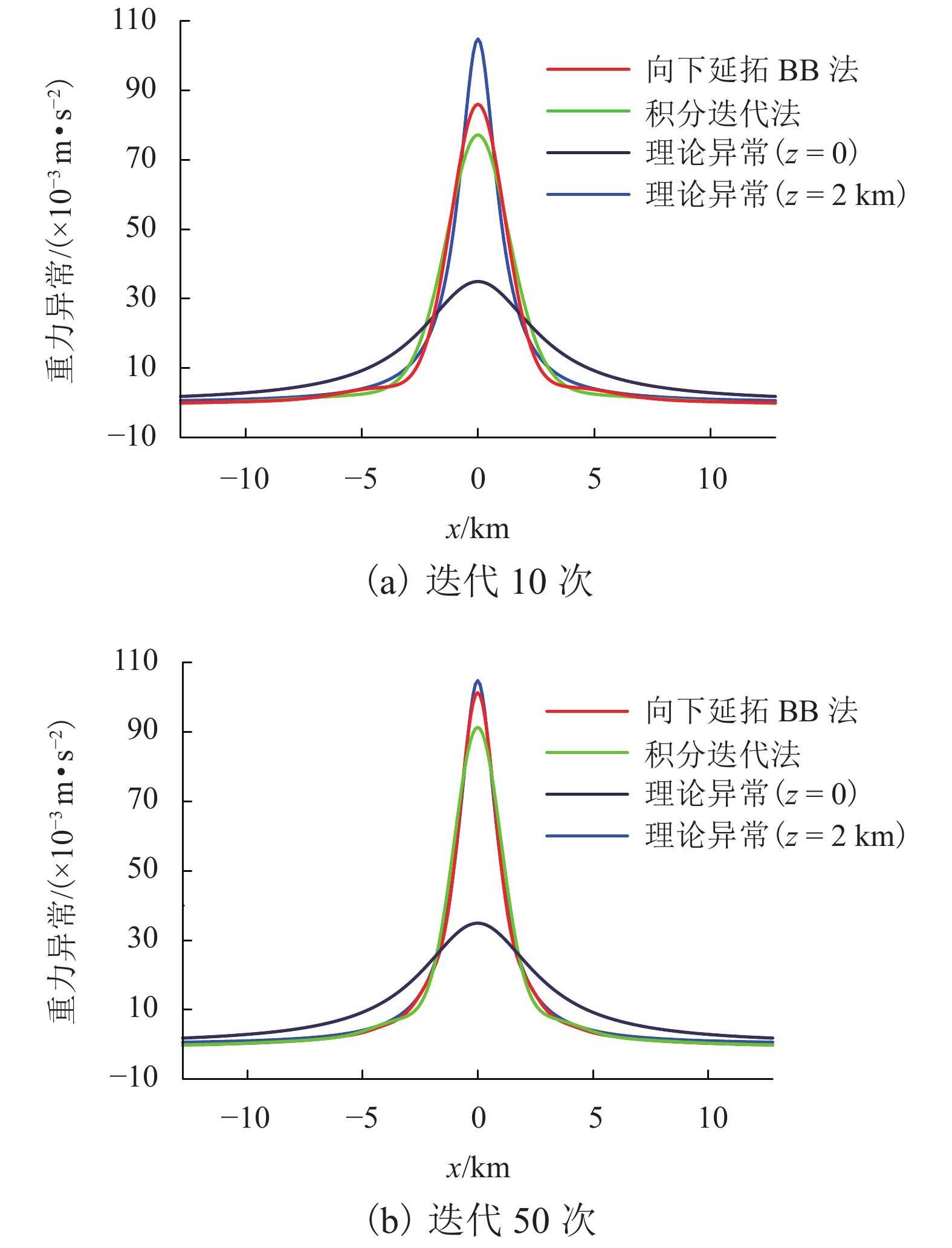
摘要: 位场的向下延拓不仅仅能够提高地球物理数据解释的可靠性，在导航方面也有着重要的作用. 为了进一步提高计算精度和速度，提出了位场向下延拓的Barzilai-Borwein （BB）法. 首先证明了位场向下延拓的系数矩阵为对称的双重Toeplitz系统矩阵（block-Toeplitz-Toeplitz-block，BTTB）；其次，假定该系数矩阵为正定的条件下，采用BB法迭代求解下延方程组，并约束其迭代步长确保算法收敛；最后，分别通过理论模型无噪声数据和实际资料对BB法进行检验，并与积分迭代法进行对比. 结果表明：理论模型验证时，同一收敛精度条件下，BB法的计算速度是积分迭代法的2倍以上；实际资料检验时，在相同计算次数下，BB法与积分迭代法的平均相对误差分别为6.1%与7.7%.
-
关键词:
- 向下延拓 /
- 系数矩阵 /
- Barzilai-Borwein法 /
- 收敛性
Abstract: Downward continuation of potential fields can not only improve the reliability of geophysical data interpretation, but also plays an important role in navigation. In order to further enhance the calculation accuracy and speed of downward continuation, the Barzilai-Borwein (BB) downward continuation method is proposed. First, the coefficient matrix of downward continuation for potential fields is proved to be a symmetric block-Toeplitz-Toeplitz-block matrix (BTTB). Next, assuming that the coefficient matrix is positive definite, the BB method is used to solve the equations of downward continuation, and the iterative step is limited to ensure the convergence of the algorithm. Finally, the BB method is validated by noise-free data of the theoretical model and practical data, and compared with the integral iterative method. The results show that under the same convergence accuracy, in the case of the theoretical model, the calculation speed of BB method is more than 2 times that of integral iteration method. In the case of practical data, the average relative errors of BB method and integral iteration method are 6.1% and 7.7%, respectively.-
Key words:
- downward continuation /
- coefficient matrix /
- Barzilai-Borwein method /
- convergence
-
图 1 理论重力异常与不同方法向下延拓结果对比
Figure 1. Theoretical gravity anomaly compared with downward continuation results of different methods
图 3 不同高度面上的磁异常等值线（单位：nT）
Figure 3. Magnetic anomaly isolines at different planes (unit： nT)
图 4 理论磁异常向下延拓后的计算结果（单位：nT）
Figure 4. Calculation results of theoretical gravity anomaly after downward continuation (unit： nT)
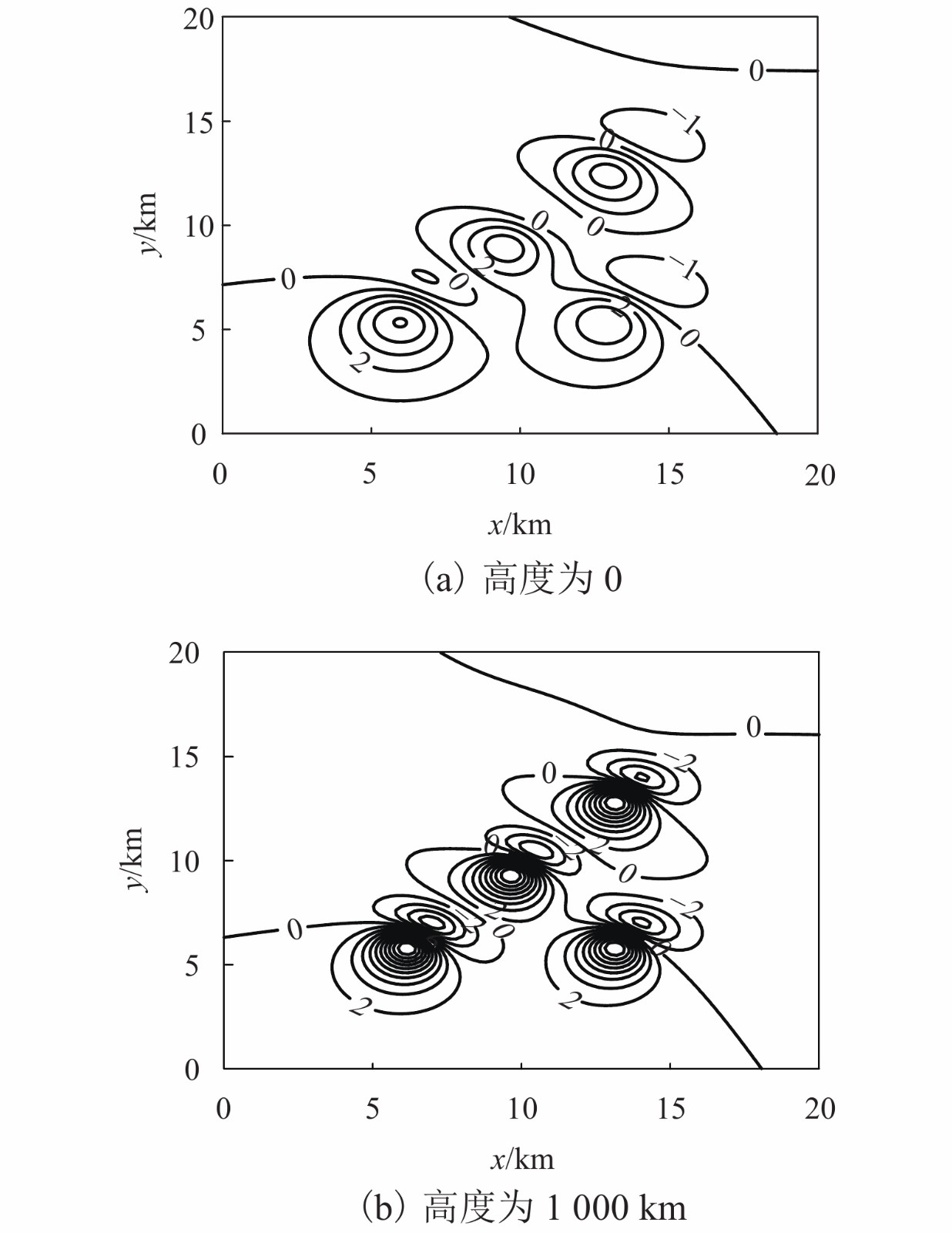
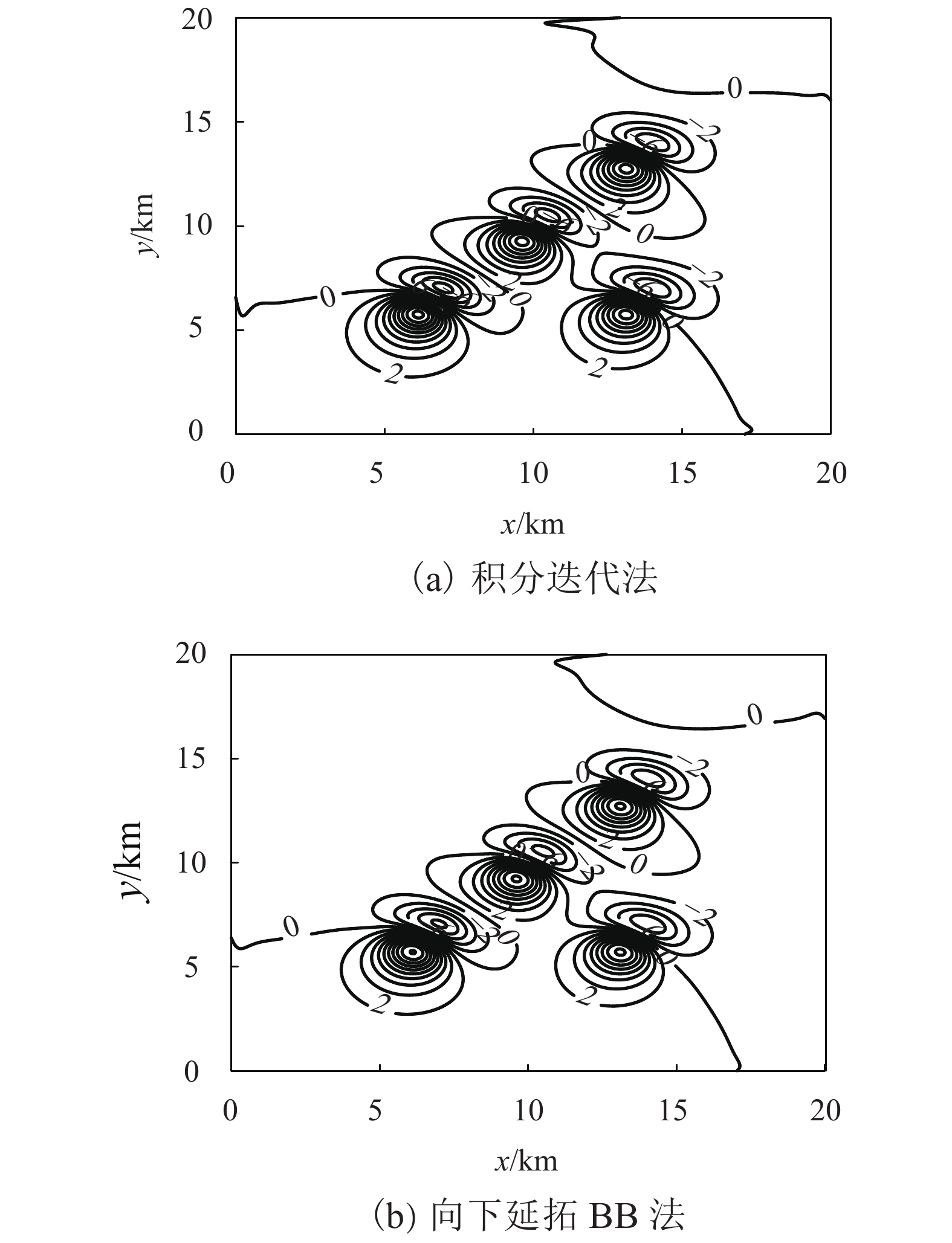
表 1 三维组合圆球型磁异常体参数
Table 1. Magnetic anomaly parameters of 3D combination sphere
模型编号 ${x_0}/$km ${{{y}}_0}/$km ${ { {h} }_0}/$km ${ { { {\textit{r} } } }_0}/$km ${M_0}/$（A•m−1） ${I_0}/$（°） ${A_0}/$（°） $I'/$（°） $A'/$（°） 1 13.5 6.5 2.5 0.5 1.0 50 60 30 60 2 6.5 6.5 2.5 0.5 1.2 50 60 30 60 3 10.0 10.0 2.5 0.5 1.0 50 60 30 60 4 13.5 13.5 2.5 0.5 1.0 50 60 30 60 
下载: 导出CSV
-
徐世浙,曹洛华,姚敬金. 重力异常三维反演-视密度成像方法技术的应用[J]. 物探与化探,2007,31(1): 25-28.XU Shizhe, CAO Luohua, YAO Jingjin. 3D inversion of gravity anomaly:an application of the apparent density imagery technology[J]. Geophysical & Geochemical Exploration, 2007, 31(1): 25-28. 徐世浙,余海龙,李海霞,等. 基于位场分离与延拓的视密度反演[J]. 地球物理学报,2009,52(6): 1592-1598. doi: 10.3969/j.issn.0001-5733.2009.06.021XU Shizhe, YU Hailong, LI Haixia, et al. The inversion of apparent density based on the separation and continuation of potential field[J]. Chinese Journal of Geophysics, 2009, 52(6): 1592-1598. doi: 10.3969/j.issn.0001-5733.2009.06.021 徐世浙,王华军,余海龙,等. 普光气田重力异常的视密度反演[J]. 地球物理学报,2009,52(9): 2357-2363. doi: 10.3969/j.issn.0001-5733.2009.09.021XU Shizhe, WANG Huajun, YU Hailong, et al. Apparent density inversion of gravity anomalies of Puguang gas field[J]. Chinese Journal of Geophysics, 2009, 52(9): 2357-2363. doi: 10.3969/j.issn.0001-5733.2009.09.021 杨金玉,徐世浙,余海龙,等. 视密度反演在东海及邻区重力异常解释中的应用[J]. 地球物理学报,2008,51(6): 1909-1916. doi: 10.3321/j.issn:0001-5733.2008.06.034YANG Jinyu, XU Shizhe, YU Hailong, et al. Application of apparent density inversion method in the east China sea and its adjacent area[J]. Chinese Journal of Geophysics, 2008, 51(6): 1909-1916. doi: 10.3321/j.issn:0001-5733.2008.06.034 徐世浙,张秀达,张昌达. 水下磁定位的若干问题[J]. 海军大连舰艇学院学报,2007,30(3): 4-6.XU Shizhe, ZHANG Xiuda, ZHANG Changda. Several problems of underwater magnetic location[J]. Journal of Dalian Naval Academy, 2007, 30(3): 4-6. 许大欣. 利用重力异常匹配技术实现潜艇导航[J]. 地球物理学报,2005,48(4): 812-816. doi: 10.3321/j.issn:0001-5733.2005.04.012XU Daxin. Using gravity anomaly matching techniques to implement submarine navigation[J]. Chinese Journal of Geophysics, 2005, 48(4): 812-816. doi: 10.3321/j.issn:0001-5733.2005.04.012 杨昆,康戈文,李洪. 重力场和地磁场综合匹配在导航中的应用[J]. 航海工程,2010,39(1): 129-816.YANG Kun, KANG Gewen, LI Hong. Application of gravity and geomagnetism matching in navigation[J]. Ship & Ocean Engineering, 2010, 39(1): 129-816. 彭富清. 地磁模型与地磁导航[J]. 海洋测绘,2006,26(2): 73-75. doi: 10.3969/j.issn.1671-3044.2006.02.021PENG Fuqing. Geomagnetic model and geomagnetic navigation[J]. Hydrographic Surveying and Charting, 2006, 26(2): 73-75. doi: 10.3969/j.issn.1671-3044.2006.02.021 王向磊,田艳峰. 基于地磁场的自主导航研究[J]. 地球物理学报,2010,53(11): 2724-2731.WANG Xianglei, TIAN Yanfeng. Automous navigation based geomagnetic research[J]. Chinese Journal of Geophysics, 2010, 53(11): 2724-2731. EVJEN H M. The place of the vertical gradient in gravitational interpretations[J]. Geophysics, 1936, 1: 127-136. doi: 10.1190/1.1437067 PETERS L J. The direct approach to magnetic interpretation and its practical application[J]. Geophysics, 1949, 14: 290-320. doi: 10.1190/1.1437537 FEDI M, FLORIO G. A stable downward continuation by using the ISVD method[J]. Geophysical Journal International, 2002, 151(1): 146-156. doi: 10.1046/j.1365-246X.2002.01767.x ZHOU Wenna, LI Jiyuan, YUAN Yuan. Downward continuation of potential field data based on Chebyshev-Pade approximation function[J]. Pure and Applied Geophysics, 2017, 175: 275-286. DAMPNEY C N G. The equivalent source technique[J]. Geophysics, 1969, 34(1): 39-53. doi: 10.1190/1.1439996 SYBERG F J R. Potential field continuation between general surfaces[J]. Geophysical Prospecting, 2010, 20(2): 267-282. doi: 10.1111/j.1365-2478.1972.tb00632.x EMILIA D A. Equivalent source used as an analytic base for processing total magnetic field profiles[J]. Geophysics, 1973, 38(2): 339-348. doi: 10.1190/1.1440344 侯重初,蔡宗熹,刘奎俊. 剖面曲线上的位场转换系统[J]. 地球物理学报,1984,27(6): 573-581. doi: 10.3321/j.issn:0001-5733.1984.06.007HOU Chongchu, CAI Zongxi, LIU Kuijun. Potential transformation techniques on an undulating observed profile[J]. Chinese Journal of Geophysics, 1984, 27(6): 573-581. doi: 10.3321/j.issn:0001-5733.1984.06.007 侯重初,蔡宗熹,刘奎俊. 从单层位出发建立曲面上的位场转换解释系统[J]. 物化探计算技术,1985,7(2): 99-107.HOU Chongchu, CAI Zongxi, LIU Kuijun. Establishing an interpretation system of potential field transformation on an uneven surface from the potential of a single layer[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1985, 7(2): 99-107. 黄翼坚,王万银,于长春. 等效源法三维随机点位场数据处理和转化[J]. 地球物理学进展,2009,24(1): 95-101.HUANG Yijian, WANG Wanyin, YU Changchun. Processing and transform of 3D arbitrarily distributed potential filed data using an equivalent source approach[J]. Progress in Geophysics, 2009, 24(1): 95-101. 刘天佑,杨宇山,李媛媛,等. 大型积分方程降阶解法与重力资料曲面延拓[J]. 地球物理学报,2007,50(1): 290-296. doi: 10.3321/j.issn:0001-5733.2007.01.036LIU Tianyou YANG Yushan, LI Yuanyuan, et al. The order depression solution for large scale integral equation and its application in the reduction of gravity data to a horizontal plane[J]. Chinese Journal of Geophysics, 2007, 50(1): 290-296. doi: 10.3321/j.issn:0001-5733.2007.01.036 徐世浙. 位场大深度向下延拓[J]. 物探化探计算技 术, 2006, 28（增）: 29-31.XU Shizhe. Downward continuation for potential field to a deeper level[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2006, 28(S): 29-31. 徐世浙. 迭代法与FFT法位场向下延拓效果的比较[J]. 地球物理学报,2007,50(1): 285-289. doi: 10.3321/j.issn:0001-5733.2007.01.035XU Shizhe. A comparison of effects between the iteration method and FFT for downward continuation of potential fields[J]. Chinese Journal of Geophysics, 2007, 50(1): 285-289. doi: 10.3321/j.issn:0001-5733.2007.01.035 徐世浙,余海龙. 位场曲化平的插值-迭代法[J]. 地球物理学报,2007,50(6): 1811-1815. doi: 10.3321/j.issn:0001-5733.2007.06.022XU Shizhe, YU Hailong. The interpolation-iteration method for potential field continuation from undulating surface to plane[J]. Chinese Journal of Geophysics, 2007, 50(6): 1811-1815. doi: 10.3321/j.issn:0001-5733.2007.06.022 陈生昌,肖鹏飞. 位场向下延拓的波数域广义逆算法[J]. 地球物理学报,2007,50(6): 1816-1822. doi: 10.3321/j.issn:0001-5733.2007.06.023CHEN Shengchang, XIAO Pengfei. Wavenumber domain generalized inverse algorithm for potential field downward continuation[J]. Chinese Journal of Geophysics, 2007, 50(6): 1816-1822. doi: 10.3321/j.issn:0001-5733.2007.06.023 郝燕玲,成怡,孙枫,等. Tikhonov正则化向下延拓方法仿真实验研究[J]. 仪器仪表学报,2008,29(3): 605-609. doi: 10.3321/j.issn:0254-3087.2008.03.030HAO Yanling, CHENG Yi, SUN Feng, et al. Simulation research on Tikhonov regulation algorithm in downward continuation[J]. Chinese Journal of Scientific Instrument, 2008, 29(3): 605-609. doi: 10.3321/j.issn:0254-3087.2008.03.030 周军,施桂国,葛致磊. 地球物理导航中位场下延的迭代正则化方法研究[J]. 宇航学报,2011,32(4): 787-794. doi: 10.3873/j.issn.1000-1328.2011.04.013ZHOU Jun, SHI Guiguo, GE Zhilei. Study of iterative regularization methods for potential field downward continuation in geophysical navigation[J]. Journal of Astronautics, 2011, 32(4): 787-794. doi: 10.3873/j.issn.1000-1328.2011.04.013 高玉文,骆遥,文武. 补偿向下延拓方法研究及应用[J]. 地球物理学报,2012,55(8): 2747-2756. doi: 10.6038/j.issn.0001-5733.2012.08.026GAO Yuwen, LUO Yao, WEN Wu. The compensation method for downward continuation of potential field from horizontal plane and its application[J]. Chinese Journal of Geophysics, 2012, 55(8): 2747-2756. doi: 10.6038/j.issn.0001-5733.2012.08.026 曾小牛,李夕海,韩绍卿,等. 位场向下延拓三种迭代方法之比较[J]. 地球物理学进展,2011,26(3): 908-915. doi: 10.3969/j.issn.1004-2903.2011.03.016ZENG Xiaoniu, LI Xihai, HAN Shaoqin, et al. A comparison of three iteration methods for downward continuation of potential fields[J]. Progress in Geophysics, 2011, 26(3): 908-915. doi: 10.3969/j.issn.1004-2903.2011.03.016 曾小牛,刘代志,牛超,等. 改进高斯-牛顿法的位场向下延拓[J]. 测绘学报,2014,43(1): 37-44.ZENG Xiaoniu, LIU Daizhi, NIU Chao, et al. A modified Gauss-Newton method for downward continuation of potential field[J]. Acta Geodaetica et Gartographica Sinica, 2014, 43(1): 37-44. 陈龙伟,张辉,郑志强,等. 水下地磁辅助导航中地磁场延拓方法[J]. 中国惯性技术学报,2007,15(6): 693-697. doi: 10.3969/j.issn.1005-6734.2007.06.013CHEN Longwei, ZHANG Hui, ZHENG Zhiqiang, et al. Technique of geomagnetic field continuation in underwater geomagnetic aided navigation[J]. Journal of Chinese Inertial Technology, 2007, 15(6): 693-697. doi: 10.3969/j.issn.1005-6734.2007.06.013 曾小牛,李夕海,贾维敏,等. 位场各阶垂向导数换算的新正则化方法[J]. 地球物理学报,2015,58(4): 1400-1410. doi: 10.6038/cjg20150426ZENG Xiaoniu, LI Xihai, JIA Weimin, et al. A new regularization method for calculating the vertical derivatives of the potential field[J]. Chinese Journal of Geophysics, 2015, 58(4): 1400-1410. doi: 10.6038/cjg20150426 XU Shizhe, YANG Jinyu, YANG Changfu, et al. The iteration method for downward continuation of a potential field from a horizontal plane[J]. Geophysical Prospecting, 2007, 55: 883-890. doi: 10.1111/j.1365-2478.2007.00634.x 张辉,陈龙伟,任治新,等. 位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究[J]. 地球物理学报,2009,52(4): 1107-1113. doi: 10.3969/j.issn.0001-5733.2009.04.028ZHANG Hui, CHEN Longwei, REN Zhixin, et al. Analysis on convergence of iteration method for potential fields downward continuation and research on robust downward continuation method[J]. Chinese Journal of Geophysics, 2009, 52(4): 1107-1113. doi: 10.3969/j.issn.0001-5733.2009.04.028 刘东甲,洪天求,贾志海,等. 位场向下延拓的波数域迭代法及其收敛性[J]. 地球物理学报,2009,52(6): 1599-1605. doi: 10.3969/j.issn.0001-5733.2009.06.022LIU Dongjia, HONG Tianqiu, JIA Zhihai, et al. Wave number domain iteration method for downward continuation of potential fields and its convergence[J]. Chinese Journal of Geophysics, 2009, 52(6): 1599-1605. doi: 10.3969/j.issn.0001-5733.2009.06.022 于波,翟国君,刘燕春,等. 噪声对磁场向下延拓迭代法的计算误差影响分析[J]. 地球物理学报,2009,52(8): 2182-2188. doi: 10.3969/j.issn.0001-5733.2009.08.029YU Bo, ZHAI Guojun, LIU Yanchun, et al. Analysis of noise effect on the calculation error of downward continuation with iteration method[J]. Chinese Journal of Geophysics, 2009, 52(8): 2182-2188. doi: 10.3969/j.issn.0001-5733.2009.08.029 王顺杰,朱海,栾禄雨. 水下地磁导航中位场积分迭代法收敛性分析[J]. 地球物理学进展,2009,24(3): 1095-1097. doi: 10.3969/j.issn.1004-2903.2009.03.040WANG Shunjie, ZHU Hai, LUAN Luyu. Constringency analysis of the iteration method for continuation of potential fields in underwater geomagnetism navigation[J]. Progress in Geophysics, 2009, 24(3): 1095-1097. doi: 10.3969/j.issn.1004-2903.2009.03.040 李星. 积分方程[M]. 北京: 科学出版社, 2008: 37-39 BATEMAN H. Some integral equations of potential theory[J]. Journal of Applied Physics, 1946, 17(2): 91-102. doi: 10.1063/1.1707698 BARZILAI J, BORWEIN J M. Two-point step size gradient methods[J]. IMA Journal of Numerical Analysis, 1988, 8(1): 141-148. doi: 10.1093/imanum/8.1.141 曾祝明. 对称Toeplitz矩阵特征值的快速算法[J]. 福建工程学院学报,2009,7(3): 301-303. doi: 10.3969/j.issn.1672-4348.2009.03.024ZENG Zhuming. A fast eigenvalue algorithm for symmetric Toeplitz matrices[J]. Journal of Fujian University of Technology, 2009, 7(3): 301-303. doi: 10.3969/j.issn.1672-4348.2009.03.024 陈龙伟,胡小平,吴美平,等. 空间与位场延拓新方法研究[J]. 地球物理学进展,2012,27(4): 1509-1518.CHEN Longwei, HU Xiaoping, WU Meiping, et al. Research on spatial domain continuation method for potential field[J]. Progress in Geophysics, 2012, 27(4): 1509-1518. 张志厚,吴乐园. 位场向下延拓的相关系数法[J]. 吉林大学学报(地球科学版),2012,42(6): 1912-1919.ZHANG Zhihou, WU Leyuan. Correlation coefficient method for downward continuation of potential fields[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(6): 1912-1919. 姚长利,郝天珧,管志宁,等. 重磁遗传算法三维反演中高速计算及有效存储方法技术[J]. 地球物理学报,2003,46(2): 252-258. doi: 10.3321/j.issn:0001-5733.2003.02.020YAO Changli, HAO Tianyao GUAN Zhining, et al. High-speed computation and efficient storage in 3D gravity and magnetic inversion based on genetic algorithms[J]. Chinese Journal of Geophysics, 2003, 46(2): 252-258. doi: 10.3321/j.issn:0001-5733.2003.02.020 王彦飞. 反问题的计算方法及其应用[M]. 北京: 高等教育出版社, 2007: 45, 49-51. 张志厚,吴乐园,王瑞赛,等. 位场向下延拓的CGNR法[J]. 中南大学学报(自然科学版),2013,44(8): 3273-3281.ZHANG Zhihou, WU Leyuan, WANG Ruisai, et al. CGNR method for potential field downward continuation[J]. Journal of Central South University (Science and Technology), 2013, 44(8): 3273-3281. 张志厚,王瑞赛. 位场向下延拓的法方程Lanczos方法[J]. 地球物理学进展,2013,28(2): 1064-1072. doi: 10.6038/pg20130261ZHANG Zhihou, WANG Ruisai. Normal equation Lanczos method for downward continuation of potential fields[J]. Progress in Geophysics, 2013, 28(2): 1064-1072. doi: 10.6038/pg20130261 张志厚. 位场向下延拓的数值计算方法[D]. 杭州: 浙江大学, 2013. 管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005: 100-101. 杨文采. 地震道的非线性混沌反演——Ⅰ. 理论和数值试验[J]. 地球物理学报,1993,36(2): 222-232. doi: 10.3321/j.issn:0001-5733.1993.02.011YANG Wencai. Nonlinear chaotic inversion of seismic traces:(I) Theory and numerical experiments[J]. Chinese Journal of Geophysics, 1993, 36(2): 222-232. doi: 10.3321/j.issn:0001-5733.1993.02.011 杨文采. 非线性地震道的混沌反演——Ⅱ. 关于Lyapunov指数和吸引子[J]. 地球物理学报,1993,36(3): 376-387. doi: 10.3321/j.issn:0001-5733.1993.03.012YANG Wencai. Nonlinear chaotic inversion of seismic traces: (II) Lyapunov exponents and attractors[J]. Chinese Journal of Geophysics, 1993, 36(3): 376-387. doi: 10.3321/j.issn:0001-5733.1993.03.012 -
下载:
点击查看大图
图(7) / 表(1)
计量
- 文章访问数: 476
- HTML全文浏览量: 235
- PDF下载量: 11
- 被引次数: 0