Hierarchical Fault Location Method for Distribution Network with Special Load
-
摘要: 特殊负荷接入配电网，增强了电源、负荷与电网之间的互动性，对故障定位提出了更高的要求，为此，提出了一种快速定位故障点的分层定位方法. 首先分析基于遗传算法的单层含特殊负荷配电网故障定位的不完备性；其次在单层模型的理论基础上，提出改进量子免疫算法的区域定位方法和隐枚举法的区段定位方法；最后对所提模型和基于单一智能算法的单层模型进行了对比仿真实验. 结果表明：与遗传算法、免疫算法和改进量子免疫算法构建的单层定位模型相比，所提分层定位方法大大简化了故障辨识模型的复杂度，在提高定位效率的同时保证了定位的容错性和稳定性，可将故障搜索维度降低69%，故障定位耗时在1 s以内，故障辨识率达到100%.Abstract: Special load is connected to the distribution network, which enhances the interaction between the power supply, load and power grid, and imposes higher requirements for fault location. To deal with this, a hierarchical location method for fast locating fault points is proposed. Firstly, the incompleteness of the genetic algorithm based fault location model is analyzed for single-layer distribution network with special load. Secondly, based on the theory of the single-layer model, a regional positioning method and a segment method are proposed, which respectively improves quantum immune algorithm and implicit enumeration method. Finally, a comparative simulation is carried out between the proposed model and the single-layer model that is based on a single intelligent algorithm. Compared with the genetic algorithm, immune algorithm and improved single-layer positioning model constructed by quantum immune algorithm, the hierarchical positioning method can greatly simplify the complexity of the fault identification model, ensure the fault tolerance and stability of the positioning while improving the positioning efficiency. In addition, this method reduces the fault search dimension by 69%, takes less than 1s to locate the fault, and the fault identification rate is 100%.
-
图 4 单层配电网故障定位仿真
Figure 4. Fault location simulation of single-layer distribution network
图 5 分层配电网故障定位仿真
Figure 5. Simulation of fault location in layered distribution network
表 1 故障区域、节点和电流方向
Table 1. Fault areas，nodes，and current directions
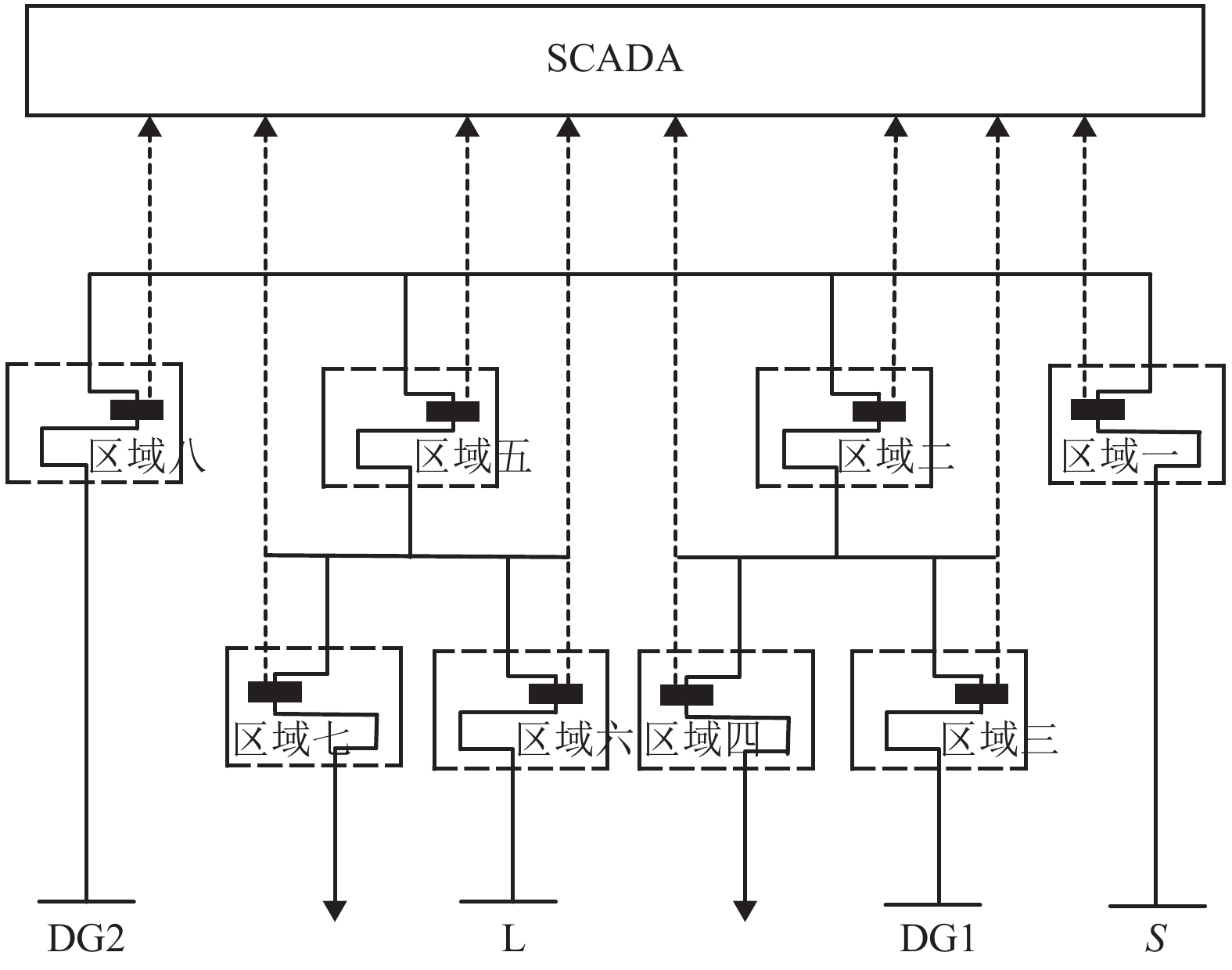
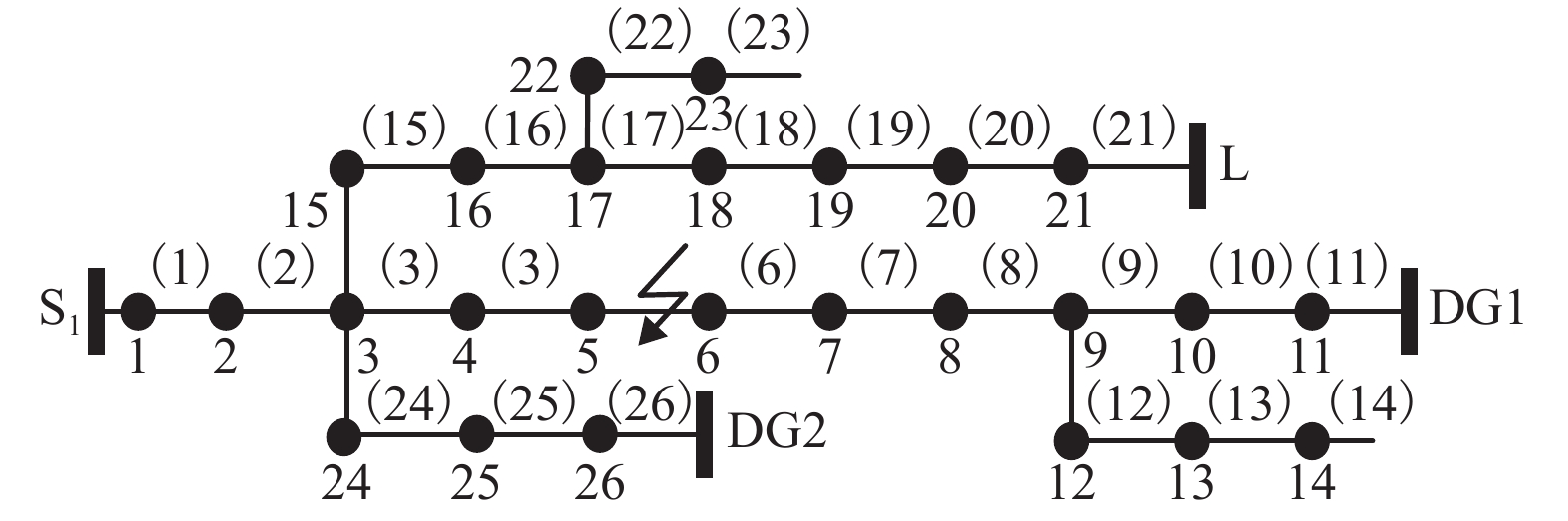
区域 区域端节点 故障电流方向 一 1 1 二 3 1 三 9 −1 四 12 0 五 15 −1 六 17 −1 七 22 0 八 24 −1 
下载: 导出CSV
表 2 单一故障仿真结果
Table 2. Single failure simulation results
假定
故障区段{K1,K2,K3} 畸变
位置区域
定位结果区段
定位结果（5） {0,0,1} 无 二 （5） （9） {0,1,1} 无 三 （9） （18） {0,1,1} 无 六 （18） （7） {1,1,1} 无 二 （7） （5） {1,1,1} 10 二 （5） （7） {1,1,1} 24 二 （7） （24） {1,1,1} 11 八 （24）
下载: 导出CSV
表 3 双重故障仿真结果
Table 3. Double-fault simulation results
假定
故障区段{K1,K2,K3} 畸变
位置区域
定位结果区段
定位结果（5）、（7） {0,0,1} 无 二 （5）、（7） （7）、（9） {0,1,1} 无 二、三 （7）、（9） （15）、（18） {0,1,1} 无 五、六 （15）、（18） （21）、（24） {1,1,1} 10 六、八 （21）、（24） （19）、（25） {1,1,1} 18 六、八 （19）、（25）
下载: 导出CSV
表 4 区段定位结果
Table 4. Segment positioning results
判断故障区域 适应度 区段状态编码 区域状态信息 二 1.000 [0 0 0 0 0 0] 0 三 0.667 [0 1 0] 1 六 0.667 [0 1 0 0 0] 1 八 1.000 [0 0 0] 0
下载: 导出CSV
表 5 4种定位模型性能对比
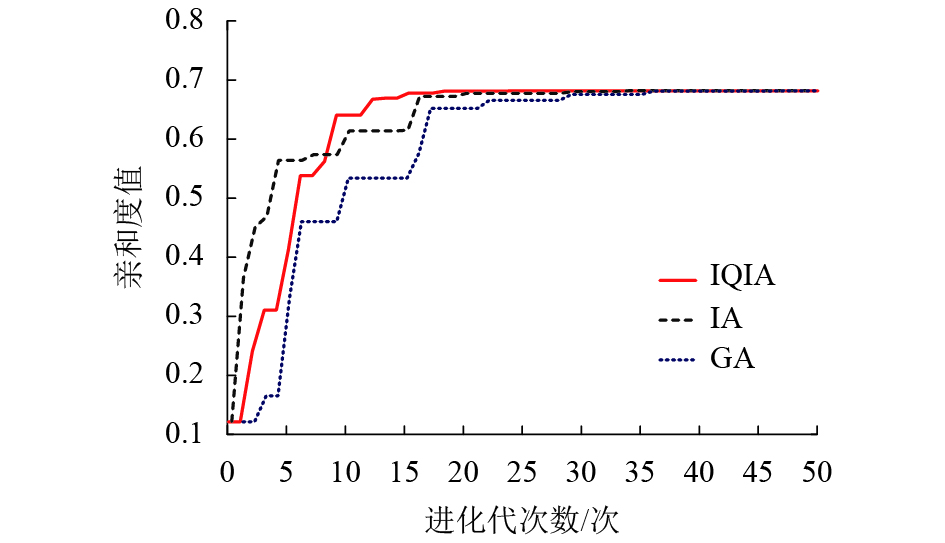
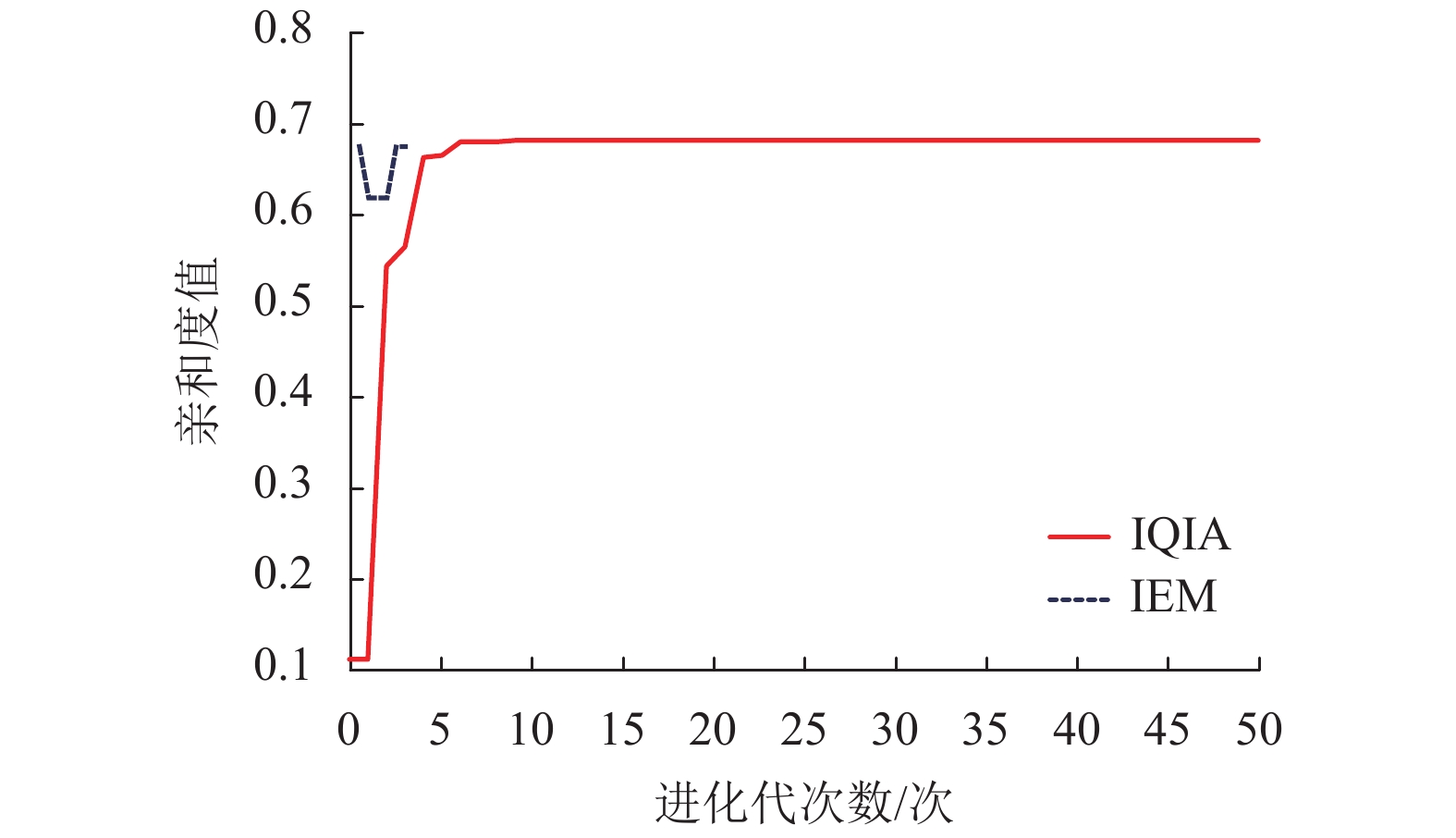
Table 5. Performance comparison of four positioning models
模型 准确次数/次 平均迭代次数/次 GA 24 36 IA 27 21 IQIA1 30 18 QIA+IEM 30 10
下载: 导出CSV
-
陈大宣,余一平,鞠平,等. 基于时变电流注入方法的特殊电力负荷建模研究[J]. 电力自动化设备,2014,34(3): 120-124. doi: 10.3969/j.issn.1006-6047.2014.03.020CHEN Daxuan, YU Yiping, JU Ping, et al. Research on special power load modeling based on time-varying current injection method[J]. Electric Power Automation Equipment, 2014, 34(3): 120-124. doi: 10.3969/j.issn.1006-6047.2014.03.020 MEHRDAD M, MEHDI E A. A new fault location technique in smart distribution networks using synchronized/non-synchronized measurements[J]. IEEE Transactions on Power Delivery, 2018, 33(3): 1358-1368. ZHU J, LUBKEMAN D L, GIRGIS A A. Automated fault location and diagnosis on electric power distribution feeders[J]. IEEE Transactions on Power Delivery, 12(2): 801-809. KNOPP T, WEBER A. Local system matrix compression for efficient reconstruction in magnetic particle imaging[J]. Advances in Mathematical Physics, 2015, 2015: 1-7. 黄佳乐,杨冠鲁. 配电网故障区间定位的改进矩阵算法[J]. 电力系统保护与控制,2014(11): 41-45. doi: 10.7667/j.issn.1674-3415.2014.11.007HUANG Jiale, YANG Guanlu. Improved matrix algorithm for fault interval location in distribution network[J]. Power System Protection and Control, 2014(11): 41-45. doi: 10.7667/j.issn.1674-3415.2014.11.007 童晓阳,张绍迅. 基于灰色关联度的配电网故障区段定位与类型识别方法[J]. 电力系统自动化,2019(4): 113-118,145. doi: 10.7500/AEPS20180214007TONG Xiaoyang, ZHANG Shaoxun. Fault segment location and type identification method for distribution network based on grey correlation degree[J]. Automation of Electric Power System, 2019(4): 113-118,145. doi: 10.7500/AEPS20180214007 郑涛,潘玉美,郭昆亚,等. 基于免疫算法的配电网故障定位方法研究[J]. 电力系统保护与控制,2014(1): 87-93.ZHENG Tao, PAN Yumei, GUO Kunya, et al. Research on fault location method of distribution network based on immune algorithm[J]. Power System Protection and Control, 2014(1): 87-93. LIANG R, PENG N, YANG Z, et al. A novel single-phase-to-earth fault location method for distribution network based on zero-sequence components distribution characteristics[J]. International Journal of Electrical Power & Energy Systems, 2018, 102: 11-22. 高云龙,周羽生,彭湃,等. 优化和声算法在含DG电网故障定位中的应用[J]. 电力系统保护与控制,2014(19): 26-31. doi: 10.7667/j.issn.1674-3415.2014.19.004GAO Yunlong, ZHOU Yusheng, PENG Pai, et al. Application of optimized harmonic algorithm in fault location of DG distribution network[J]. Power System Protection and Control, 2014(19): 26-31. doi: 10.7667/j.issn.1674-3415.2014.19.004 刘蓓,汪沨,陈春,等. 和声算法在含DG配电网故障定位中的应用[J]. 电工技术学报,2013,28(5): 280-284. doi: 10.3969/j.issn.1000-6753.2013.05.039LIU Pei, WANG Feng, CHEN Chun, et al. Application of harmonic algorithm in fault location of DG distribution network[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 280-284. doi: 10.3969/j.issn.1000-6753.2013.05.039 陈奎,张云,王洪寅,等. 基于免疫算法的含分布式电源配电网的故障定位[J]. 电力系统保护与控制,2017,45(24): 57-62. doi: 10.7667/PSPC161985CHEN Kui, ZHANG Yun, WANG Hongyin, et al. Fault location based on immune algorithm with distributed power distribution network[J]. Power System Protection and Control, 2017, 45(24): 57-62. doi: 10.7667/PSPC161985 束洪春,董俊,段锐敏,等. 基于自然频率的辐射状配电网分层分布式ANN故障定位方法[J]. 电力系统自动化,2014,38(5): 83-89.SHU Hongchun, DONG Jun, DUAN Ruimin, et al. Hierarchical distributed ANN fault location method for radial distribution network based on natural frequency[J]. Automation of Electric Power Systems, 2014, 38(5): 83-89. 何瑞江,胡志坚,李燕,等. 含分布式电源配电网故障区段定位的线性整数规划方法[J]. 电网技术,2018,42(11): 3684-3692.HE Ruijiang, HU Zhijian, LI Yan, et al. Linear integer programming method for fault segment location of distributed power distribution network[J]. Power System Technology, 2018, 42(11): 3684-3692. 贺仁睦,王吉利,史可琴. 实测冲击负荷分析与建模[J]. 中国电机工程学报,2010,30(25): 59-65.HE Renmu, WANG Jili, SHI Keqin, et al. Analysis and modeling of measured impact load[J]. Proceedings of the CSEE, 2010, 30(25): 59-65. 刘鹏程,李新利. 基于多种群遗传算法的含分布式电源的配电网故障区段定位算法[J]. 电力系统保护与控制,2016(2): 36-41. doi: 10.7667/j.issn.1674-3415.2016.02.005LIU Pengcheng, LI Xinli. Fault segment location algorithm for distribution network with distributed power based on multi-population genetic algorithm[J]. Power System Protection and Control, 2016(2): 36-41. doi: 10.7667/j.issn.1674-3415.2016.02.005 郭壮志,陈涛,黄全振,等. 配电网故障定位的层级模型及其预测校正算法[J]. 电力自动化设备,2018,38(7): 56-65.GUO Zhuangzhi, CHEN Tao, HUANG Quanzhen, et al. Hierarchical model of fault location in distribution network and its prediction correction algorithm[J]. Electric Power Automation Equipment, 2018, 38(7): 56-65. 王秋杰,金涛,谭洪,等. 基于分层模型和智能校验算法的配电网故障定位技术[J]. 电工技术学报,2018,33(22): 5327-5337.WANG Qiujie, JIN Tao, TAN Hong,, et al. Fault location technology of distribution network based on hierarchical model and intelligent check algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5327-5337. 焦李成, 李阳阳, 刘芳. 量子计算、优化与学习[M]. 北京: 科学出版社, 2017: 8-15. 祝志慧,孙云莲. 量子免疫算法在电网故障诊断中的应用[J]. 电力系统保护与控制,2010(10): 28-31,36.ZHU Zhihui, SUN Yunlian. Application of quantum immune algorithm in power grid fault diagnosis[J]. Power System Protection and Control, 2010(10): 28-31,36. -
下载:
点击查看大图
图(5) / 表(5)
计量
- 文章访问数: 525
- HTML全文浏览量: 234
- PDF下载量: 11
- 被引次数: 0