Bending Capacity Calculation Method for Corroded Reinforced Concrete Beams
-
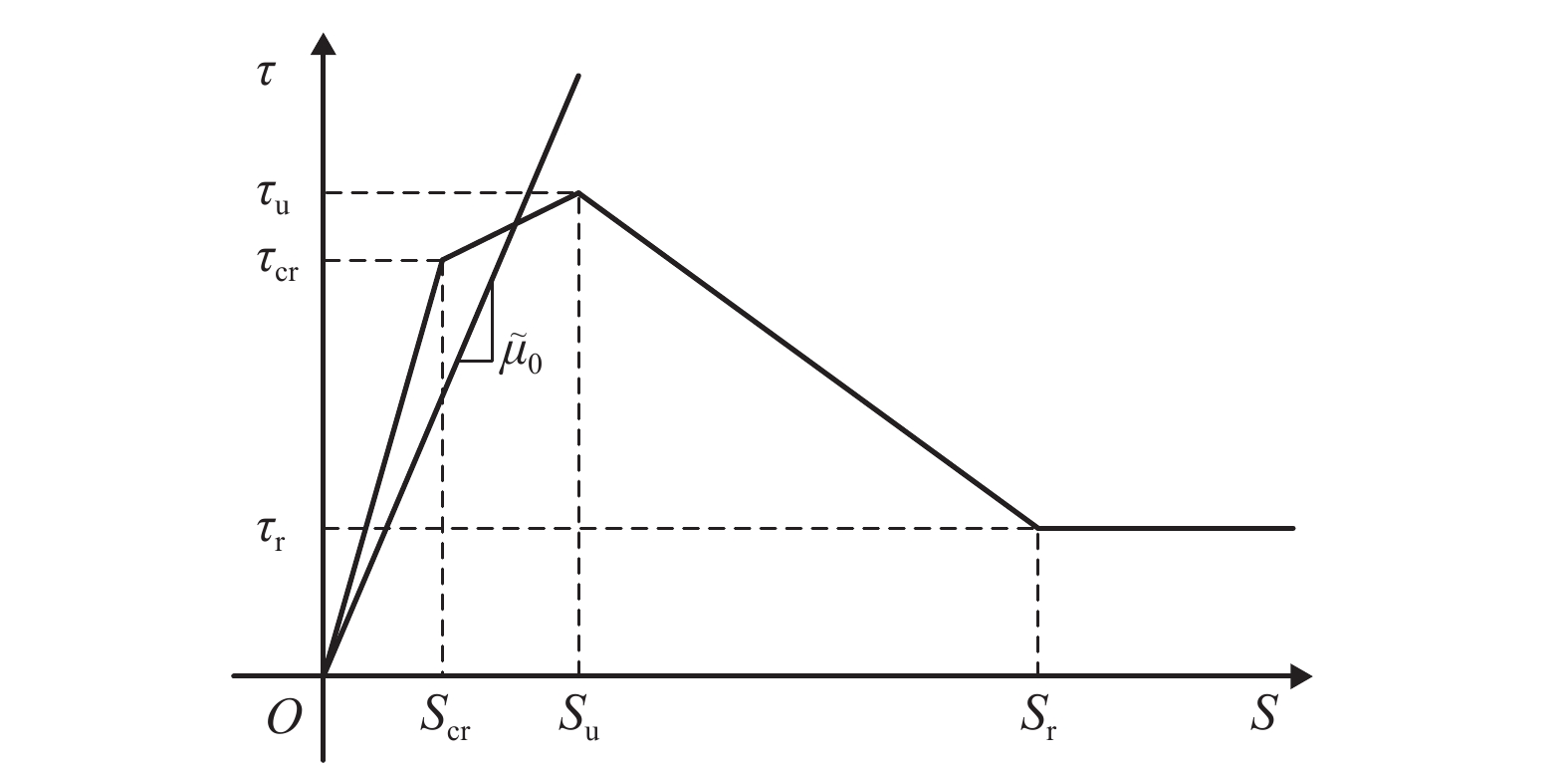
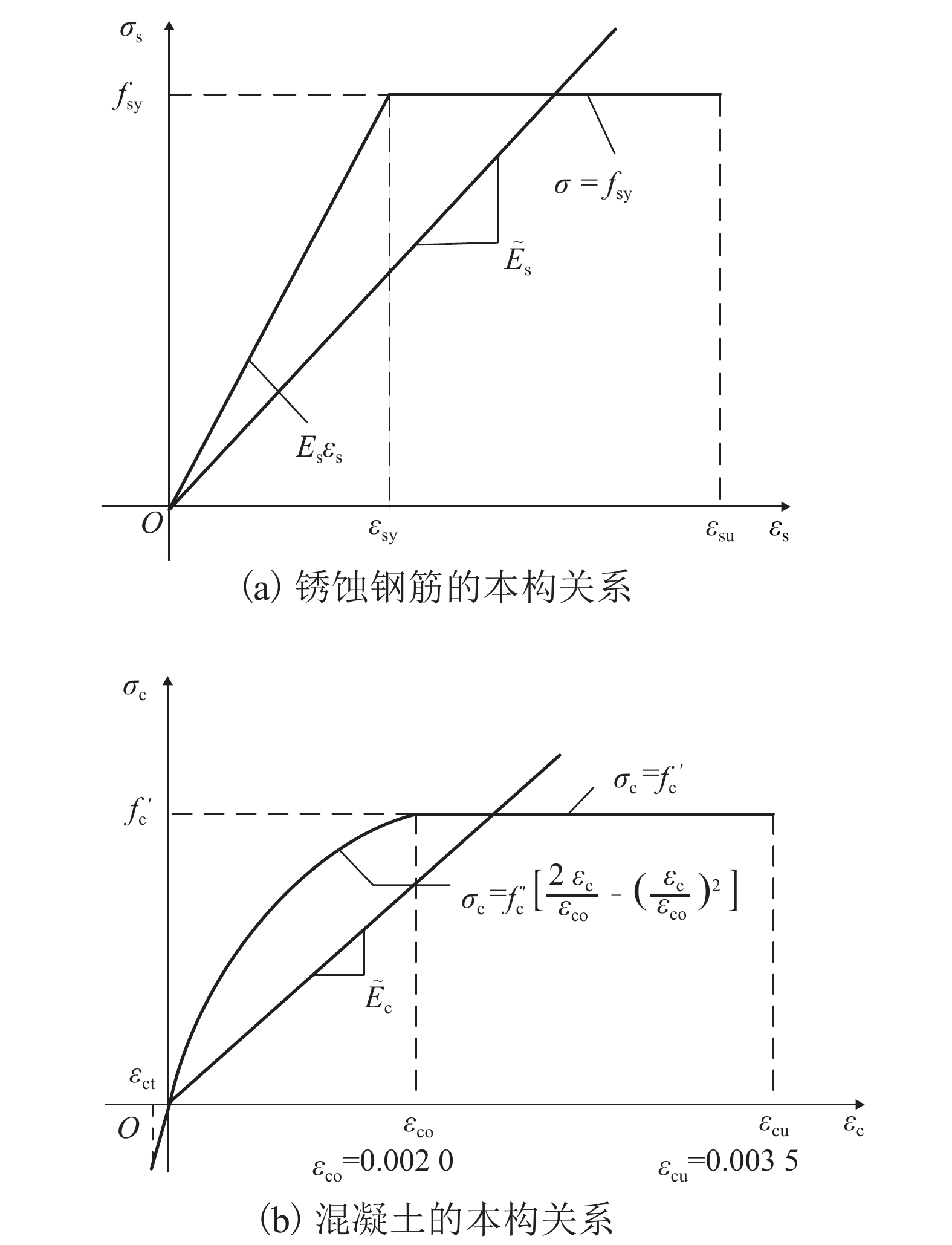
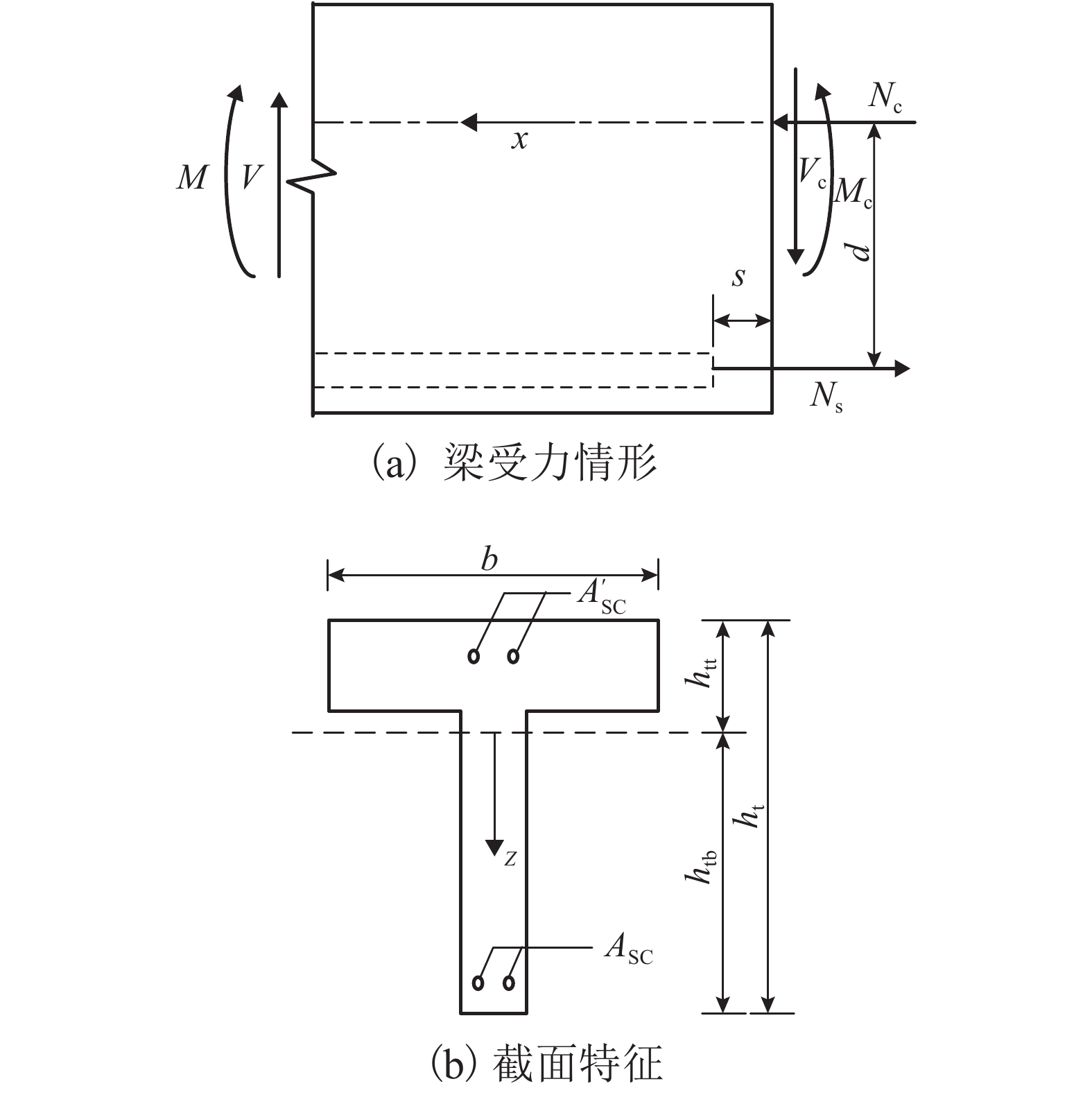
摘要: 工程中钢筋混凝土梁纵向受力钢筋锈蚀情况复杂，梁上作用荷载形式多变. 为获取锈蚀RC （reinforced concrete）梁的抗弯承载能力，以锈蚀钢筋混凝土简支梁为研究对象，将锈蚀RC梁视为由混凝土和锈蚀底部纵筋组成的存在粘结-滑移的组合梁，依据混凝土与锈蚀钢筋之间的变形协调条件，给出了以挠度表达的锈蚀RC简支梁平衡微分方程；将平衡微分方程的齐次解作为单元形函数，推导出了锈蚀钢筋混凝土梁的单元刚度矩阵、等效节点荷载列阵以及每一荷载步锈蚀梁的内力计算公式；建立了能准确反应简支梁上荷载作用形式以及钢筋锈蚀状况的锈蚀RC梁抗弯承载力计算模型；最后通过17根锈蚀RC简支梁的试验数据对建议计算方法进行验证. 验证结果表明，抗弯承载力试验值与计算值之比的平均值为1.06，方差为0.012，二者吻合良好，该计算方法准确.Abstract: The corrosion state of longitudinally stressed steel bars in corroded reinforced concrete beams is very complicated. Moreover, the form of the load applied to beams is variable. In order to obtain the bending capacity of corroded RC (reinforced concrete) beams, the corroded RC beam with simple support is taken as the object, which is regarded as a composite beam composed of steel bars and concrete with bond and slip. Based on the deformation coordination conditions between corroded steel bars and concrete, the equilibrium differential equation of corroded reinforced concrete beam is expressed by deflection. By the homogeneous solution of the differential equilibrium equation that is used as the unit shape function, the element stiffness matrix, the equivalent node load matrix, and the internal force calculation formula of the corroded reinforced concrete beam is derived under each load step. The calculation method for the bending capacity of corroded reinforced concrete beams which can reflect the corrosion condition of the steel and the load form is established. The analytical method is validated with the test data of 17 corroded reinforced concrete beams. The average ratio of test results to predicted results is 1.06 and the variance is 0.012, which shows good agreement between test and prediction results, and desirable accuracy of the calculation method.
-
Key words:
- reinforced concrete /
- simple supported beam /
- corrosion /
- stiffness matrix /
- bending capacity /
- calculation method
-
图 2 钢筋与混凝土间的粘结-滑移关系
Figure 2. Bond-slip relationship between uncorroded steel bars and concrete
图 3 锈蚀钢筋和混凝土的本构关系
Figure 3. The constitutive relation of corroded steel bars and concrete
表 1 锈蚀RC梁试验值与计算值对比表
Table 1. Comparison of flexural strength between test results and prediction results of corroded reinforced concrete beams
文献 编号 b/mm × h/mm l0/mm 锈蚀率ρw/% 受拉纵筋 fy/MPa fcMPa As′ /mm2 Msu Mju Msu /Mju [2] BT1-2-6 150 × 150 900 11.82 2 × 10 520 38.90 2 × 8 10.46 8.59 1.22 BT1-3-6 150 × 150 900 16.44 2 × 10 520 39.48 2 × 8 9.15 7.98 1.15 BT1-2-8 150 × 150 900 17.44 2 × 10 520 28.39 2 × 8 7.82 7.71 1.01 BT1-3-8 150 × 150 900 23.92 2 × 10 520 39.48 2 × 8 6.48 7.00 0.93 BT3-3-6 150 × 150 900 13.26 2 × 10 520 37.58 2 × 8 9.28 8.38 1.11 BT3-2-8 150 × 150 900 16.16 2 × 10 520 28.39 2 × 8 9.12 7.88 1.16 BT3-3-8 150 × 150 900 25.04 2 × 10 520 28.39 2 × 8 6.60 6.74 0.98 [9] BA I-5 150 × 200 1 200 7.39 216 425.47 25.93 212 21.37 22.13 0.97 BA I-6 150 × 200 1 200 8.37 216 425.47 25.93 212 20.00 21.82 0.92 BA I-7 150 × 200 1 200 9.91 216 425.47 25.93 212 20.84 21.33 0.98 BA I-8 150 × 200 1 200 10.08 216 425.47 25.93 212 19.22 21.28 0.90 BA I-9 150 × 200 1 200 11.55 216 425.47 25.93 212 18.34 20.82 0.88 BB II-5 150 × 200 1 200 6.60 216 574.56 35.55 212 35.88 30.29 1.18 BB II-6 150 × 200 1 200 7.16 216 574.56 35.55 212 33.08 30.05 1.10 BB II-7 150 × 200 1 200 8.65 216 574.56 35.55 212 34.39 29.42 1.17 BB II-8 150 × 200 1 200 9.03 216 574.56 35.55 212 34.48 29.25 1.18 BB II-9 150 × 200 1 200 10.21 216 574.56 35.55 212 32.13 28.75 1.12 
下载: 导出CSV
-
牛荻涛. 混凝土结构耐久性与寿命预测[M]. 北京: 科学出版社, 2003: 95-96 金伟良. 腐蚀混凝土结构学[M]. 北京: 科学出版社, 2011: 83-86 ZHANG W P, YE Z W, GU X L. Effects of stirrup corrosion on shear behaviour of reinforced concrete beams[J]. Structure and Infrastructure Engineering, 2017, 13(8): 1081-1092. doi: 10.1080/15732479.2016.1243563 ABUL K A, SHANSAD A, SYED A A. Residual strength of corrosion-damaged reinforced concrete beams[J]. ACI Materials Journal, 2007, 104(1): 40-47. AMGED O, ABDELATIF J O, SERENA G. 3D finite element modelling of corrosion of lap splice joints in concrete[J]. Construction and Building Materials, 2018, 169: 124-131. doi: 10.1016/j.conbuildmat.2018.02.150 ZHANG J H, LING X H, GUAN Z G. Finite element modeling of concrete cover crack propagation due to non-uniform corrosion of reinforcement[J]. Construction and Building Materials, 2017, 132: 487-499. doi: 10.1016/j.conbuildmat.2016.12.019 EYRE J R, NOKHASTEH M. Strength assessment of corrosion damaged reinforced concrete slabs and beams[C]//Proceedings of the Institution of Civil Engineers: Structures & Buildings. Telluride: ICE Publishing, 1992, 94（2）: 197-203. CAPOZUCCA R, CERRI M N. Influence of reinforcement corrosion-in the compressive zone-on the behaviour of RC beams[J]. Engineering Structures, 2003, 25(13): 1575-1583. doi: 10.1016/S0141-0296(03)00119-6 赵建昌,徐宁,杨维国. 考虑粘结滑移的锈蚀钢筋混凝土梁非线性实用分析方法研究[J]. 水力发电学报,2007,26(6): 35-40. doi: 10.3969/j.issn.1003-1243.2007.06.007ZHAO Jianchang, XU Ning. YANG Weiguo. Practical nonlinear analysis method of corroded reinforced concrete beam with bond-slip[J]. Journal of Hydroelectric Engineering, 2007, 26(6): 35-40. doi: 10.3969/j.issn.1003-1243.2007.06.007 赵建昌,徐宁. 锈蚀钢筋混凝土梁截面协同工作系数研究[J]. 水利学报,2007,38(9): 1096-1102. doi: 10.3321/j.issn:0559-9350.2007.09.011ZHAO Jianchang, XU Ning. Studies on the section coordination coefficient of corroded reinforced concrete beam[J]. Journal of Hydraulic Engineering, 2007, 38(9): 1096-1102. doi: 10.3321/j.issn:0559-9350.2007.09.011 LIU T B, LI K, LIU S W, et al. Flexural capacity calculation for a longitudinal non-uniform corroded reinforced concrete beam[J]. International Journal of Earth Sciences and Engineering, 2016, 9(1): 347-354. 袁迎曙,贾福萍,蔡跃. 锈蚀钢筋混凝土梁的结构性能退化模型[J]. 土木工程学报,2001,34(3): 47-52,96. doi: 10.3321/j.issn:1000-131X.2001.03.009YUAN Yingshu, JIA Fuping, CAI Yue. The structural behavior deterioration model for corroded reinforced concrete beams[J]. China Civil Engineering Journal, 2001, 34(3): 47-52,96. doi: 10.3321/j.issn:1000-131X.2001.03.009 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB50010—2010[S]. 北京: 中国建筑工业出版社, 2010. 江见鲸, 陆新征, 叶列平. 混凝土结构有限元分析[M]. 北京: 清华大学出版社, 2005: 91-92 -
下载:
点击查看大图
图(4) / 表(1)
计量
- 文章访问数: 5636
- HTML全文浏览量: 5417
- PDF下载量: 49
- 被引次数: 0