Analysis of Rolling Contact between Wheel and Rail in Switch Area
-
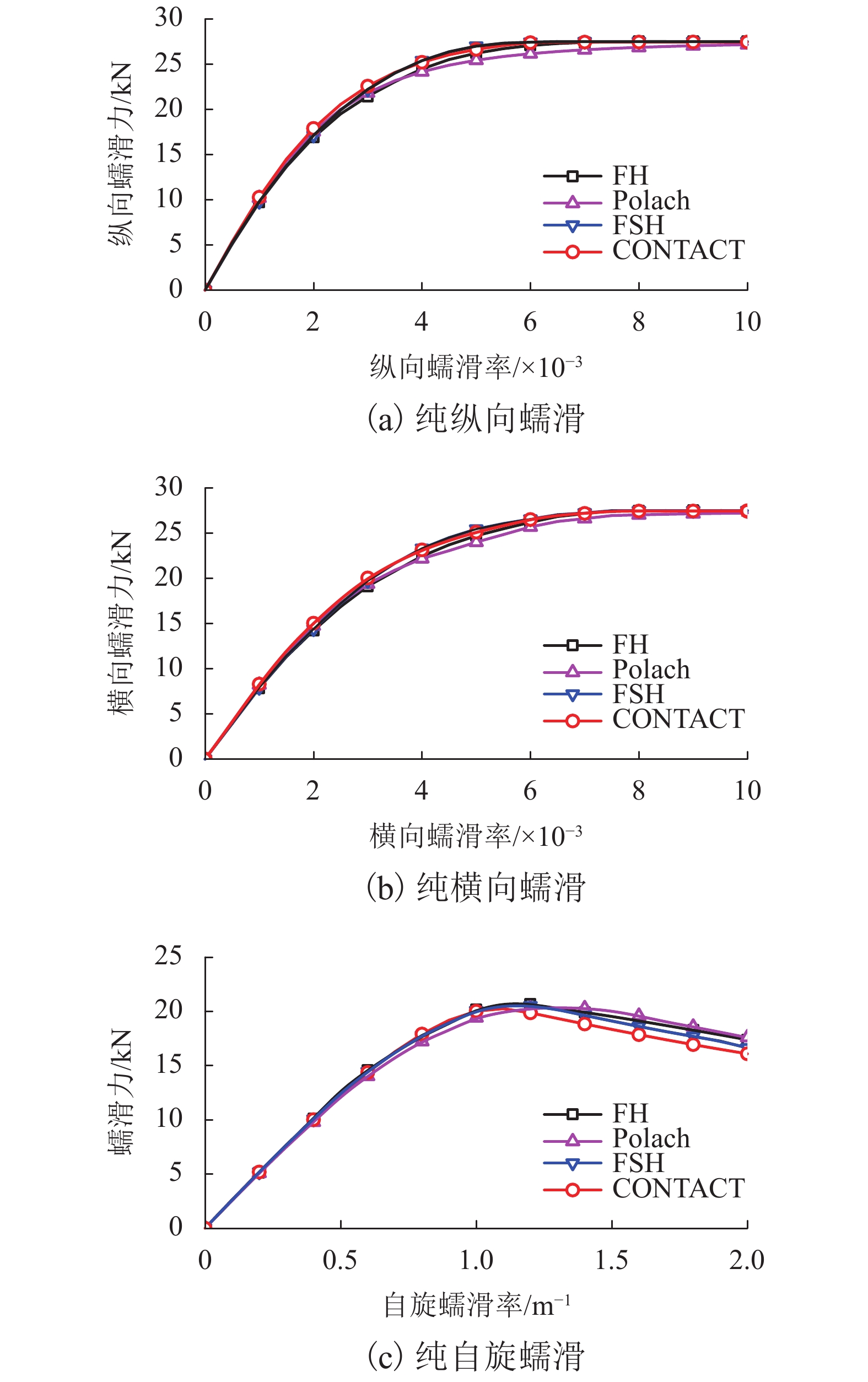
摘要: 为研究岔区轮轨匹配关系和经典轮轨接触理论对岔区的适用性，建立了岔区轮轨接触有限元模型，编写了数种岔区法向力及切向力计算程序. 以18号高速道岔转辙区及辙叉区典型断面为例，在法向对比了赫兹、半赫兹、Kalker三维非赫兹滚动接触理论与有限元模型在接触斑面积和接触应力上的差异，切向对比了基于赫兹和半赫兹的FASTSIM算法、Polach模型和CONTACT程序在不同工况下的蠕滑力差异. 计算结果表明：有限元模型考虑了轮轨材料应力应变特性，更接近实际运用工况，赫兹、半赫兹、Kalker三维非赫兹与有限元法接触斑面积分别最大相差50.42%、17.83%和24.78%，最大接触应力相差60.28%、25.25%和32.37%； 各工况下4种切向力模型蠕滑力随蠕滑率的变化趋势相同，同一工况下基于赫兹和半赫兹的FASTSIM算法和Polach模型与CONTACT计算结果最大相差8.08%、5.19%、9.70%； 综合岔区轮轨法向、切向计算精度和计算效率，半赫兹接触理论结合FASTSIM算法在岔区大批量的数据处理中更具优势.Abstract: In order to study the wheel-rail matching relationship and applicability of the classical wheel-rail contact theory in turnout area, the finite element model of the wheel-rail contact in switch area was established, and several calculation programs of the normal force and tangential force on switch were compiled. By taking the typical section of the No. 18 high-speed switch rail area and the switch frog area as an example, the contact patch area and contact stress in the rolling contact theories of the Hertz, semi-Hertz, Kalker three-dimensional non-Hertz and the finite element model are compared in the normal direction. The creep forces calculated by the FASTSIM algorithm based on Hertz and semi-Hertz, the Polach model and CONTACT are compared under different working conditions. The calculation results show that as the stress-strain characteristics of the wheel-rail material is considered in the finite element model, the result is closer to the actual working conditions. The maximum difference between the contact patch areas of Hertz, semi-Hertz, Kalker non-Hertz and finite element method 50.42%, 17.83% and 24.78%. The maximum difference in contact stress is 60.28%, 25.25% and 32.37%. Under the different working conditions, the creep force of the four tangential force models shows the same trend with the varying creep rate. Under the same working condition, the maximum difference between the creep forces calculated by CONTACT, FASTSIM algorithm based on Hertz and half Hertz and the Polach model are 8.08%, 5.19%, and 9.70%. According to the calculation accuracy of the switch in the normal and tangential directions and computational efficiency, the semi-hertz contact theory combined with the FASTSIM algorithm has advantages in large-scale data processing.
-
Key words:
- high-speed switch /
- wheel-rail matching /
- normal contact /
- tangential theory
-
图 10 Johnson-Vermeulen理论黏滑区划分
Figure 10. Stick-slip zone division by Johnson-Vermeulen theroy
表 2 辙叉区轮轨接触面积和最大接触应力
Table 2. Wheel-rail contact area and maximum contact stress in switch frog
yw/mm 赫兹理论 半赫兹理论 非赫兹理论 有限元 Aa/mm2 Pmax/MPa Aa/mm2 Pmax/MPa Aa/mm2 Pmax/MPa Aa/mm2 Pmax/MPa 0 37.83 2 722.69 55.46 2 427.55 52.94 2 565.54 63.38 1 938.12 3 37.83 2 722.69 55.39 2 430.19 52.92 2 566.51 62.64 1 972.37 6 37.83 2 722.69 55.36 2 420.86 53.00 2 553.31 61.97 1 999.42 9 36.64 2 810.99 52.05 2 547.29 50.50 2 615.74 60.22 2 071.57 
下载: 导出CSV
表 1 转辙区轮轨接触面积和最大接触应力
Table 1. Wheel-rail contact area and maximum contact stress in switch rail
yw/mm 赫兹理论 半赫兹理论 非赫兹理论 有限元 Aa/mm2 Pmax/MPa Aa/mm2 Pmax/MPa Aa/mm2 Pmax/MPa Aa/mm2 Pmax/MPa 0 92.48 1 113.84 60.31 2 326.20 56.81 2 481.08 73.40 2 045.59 3 92.48 1 113.84 63.36 2 185.94 58.31 2 336.94 74.33 1 905.11 6 77.14 1 335.22 58.49 2 216.11 53.18 2 350.47 70.70 2 063.56 9 43.01 2 394.93 72.86 1 613.36 65.80 1 766.93 86.75 1 494.23
下载: 导出CSV
-
任尊松,翟婉明,王其昌. 轮轨接触几何关系在道岔系统动力学中的应用[J]. 铁道学报,2001,23(5): 12-15.REN Zunsong, ZHAI Wanming, WANG Qichang. The use of spatial wheel/rail contact geometric relationship in the turnout system dynamics[J]. Journal of the China Railway Society, 2001, 23(5): 12-15. 丁军君,李芾,黄运华. 基于半赫兹接触的车轮磨耗计算[J]. 西南交通大学学报,2011,46(2): 195-199. doi: 10.3969/j.issn.0258-2724.2011.02.003DING Junjun, LI Fu, HUANG Yunhua. Calculation of wheel wear based on semi-Hertzian contact[J]. Journal of Southwest Jiaotong University, 2011, 46(2): 195-199. doi: 10.3969/j.issn.0258-2724.2011.02.003 HERTZ H. On the contact of elastic solids[J]. Journal für die Reine und Angewandte Mathematik, 1882, 92: 156-171. AYASSE J, CHOLLET H. Determination of the wheel rail contact patch in semi-Hertzian conditions[J]. Vehicle System Dynamics, 2005, 43(3): 161-172. doi: 10.1080/00423110412331327193 KALKER J J, JOHNSON K L. Three-dimensional elastic bodies in rolling contact[M]. Netherland: Kluwer Academic publishers, 1990: 268-272. 肖乾,车宇翔,周新建,等. 轮轨滚动接触棘轮效应数值分析[J]. 铁道学报,2013,35(12): 19-23. doi: 10.3969/j.issn.1001-8360.2013.12.003XIAO Qian, CHE Yuxiang, ZHOU Xinjian, et al. Numerical analysis on ratcheting effect of rolling contact between wheel and rail[J]. Journal of the China Railway Society, 2013, 35(12): 19-23. doi: 10.3969/j.issn.1001-8360.2013.12.003 CARTER F W. On the action of a locomotive driving wheel[J]. Proceedings of the Royal Society of London, 1926, 112(760): 151-157. JOHNSON K L. The effect of a tangential contact force on the rolling motion of an elastic sphere on a plane[J]. Journal of Applied Mechanics, 1958, 25(1): 339-346. VERMEULEN P J, JOHNSON K L. Contact of nonspherical elastic bodies transmitting tangential forces[J]. Journal of Applied Mechanics, 1964, 31(2): 338-340. doi: 10.1115/1.3629610 SHEN Z Y, HEDRICK J K, ELKINS J A. A comparison of alternative creep force models for rail vehicle dynamic analysis[J]. Vehicle System Dynamics, 1983, 12(1/2/3): 79-83. KALKER J J. On the rolling contact of two elastic bodies in the presence of dry friction[D]. The Netherland: Delft University of Technology, 1967. KALKER J J. A fast algorithm for the simplified theory of rolling contact[J]. Vehicle System Dynamics, 1982, 11(1): 1-13. doi: 10.1080/00423118208968684 POLACH O. Fast wheel-rail forces calculation computer code[J]. Vehicle System Dynamics, 2000, 33(S): 728-739. 丁军君. 基于蠕滑机理的重载货车车轮磨耗研究[D]. 成都: 西南交通大学, 2012. 徐井芒. 高速道岔曲尖轨磨耗仿真分析研究[D]. 成都: 西南交通大学, 2015. -
下载:
点击查看大图
图(11) / 表(2)
计量
- 文章访问数: 662
- HTML全文浏览量: 340
- PDF下载量: 30
- 被引次数: 0