缓和曲线正交拟合的Levenberg-Marquardt算法

宋占峰; 王健; 李军

doi:10.3969/j.issn.0258-2724.20190130

缓和曲线正交拟合的Levenberg-Marquardt算法

doi: 10.3969/j.issn.0258-2724.20190130

基金项目: 国家自然科学基金资助项目（51678574）

详细信息

作者简介:
宋占峰（1973—），男，副教授，博士，研究方向为道路与铁道线路优化设计方法，E-mail：songzhanfeng@csu.edu.cn

通讯作者:
李军（1973—），男，副教授，博士，研究方向为道路与铁道线路优化设计方法，E-mail：lijun_csu@csu.edu.cn

中图分类号: U212.3
计量
- 文章访问数: 745
- HTML全文浏览量: 192
- PDF下载量: 23
- 被引次数: 0
出版历程
- 收稿日期: 2019-03-05
- 修回日期: 2019-06-11
- 网络出版日期: 2019-09-18
- 刊出日期: 2020-02-01

Levenberg-Marquardt Algorithm for Orthogonal Fitting of Transition Curves

摘要

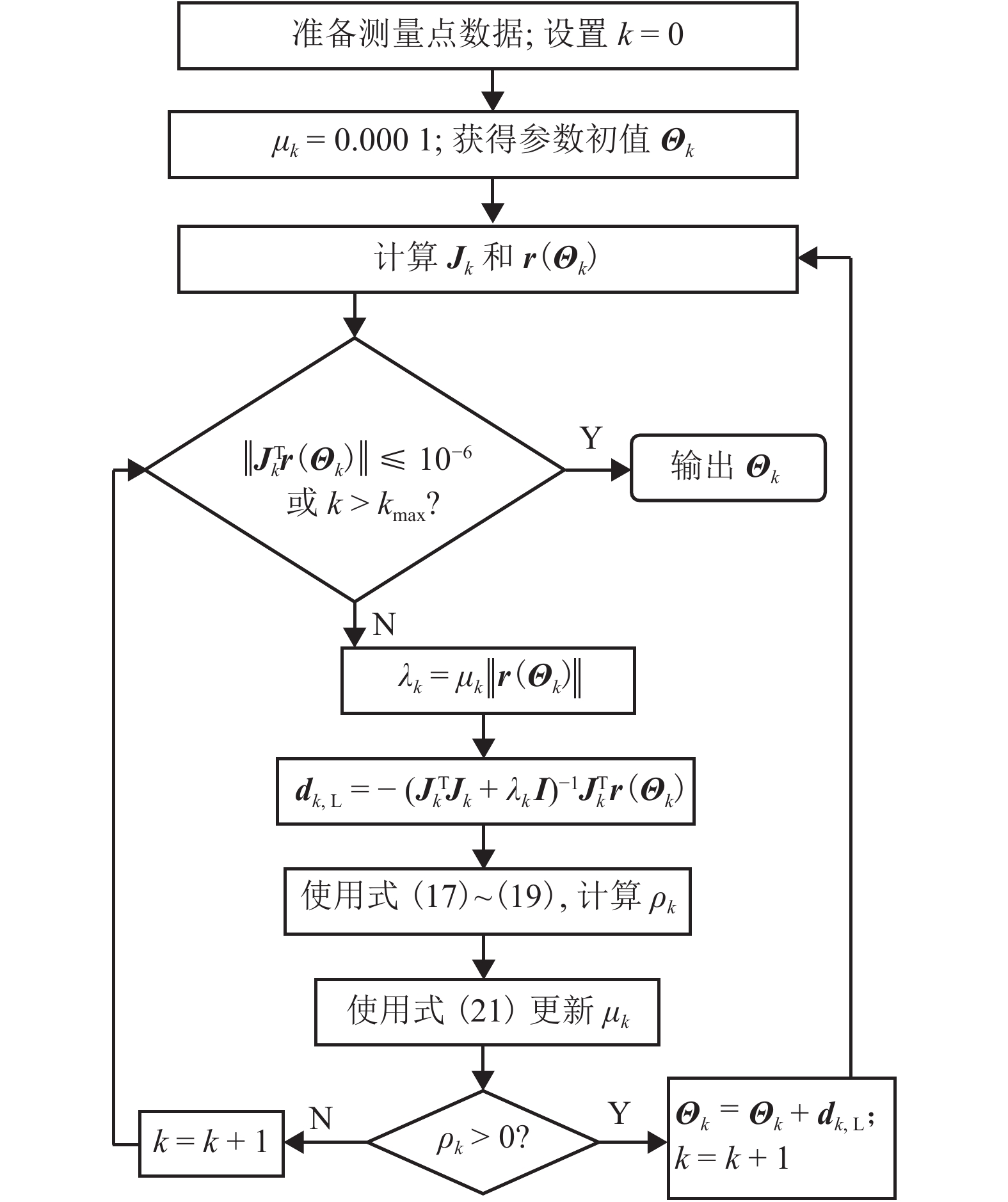
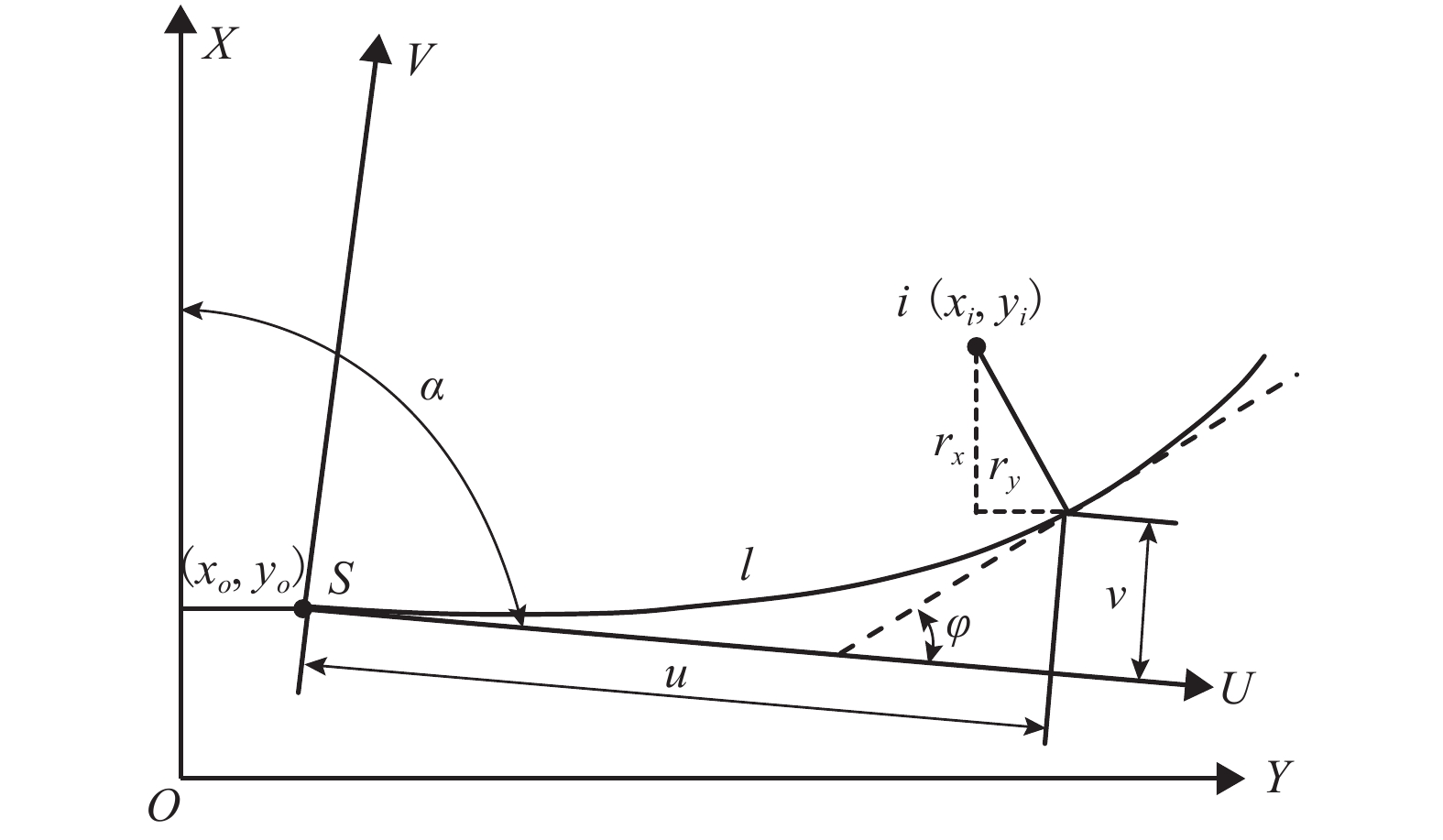
摘要: 为了由测量点识别既有线路中的缓和曲线参数，研究了基于参数方程的缓和曲线正交拟合迭代优化方法. 首先，通过特征值分析，阐明了由于病态性的存在，在迭代过程中，常规的Gauss-Newton （GN）算法会发散. 其次，提出了双目标优化模型，将GN算法与最速下降法结合，确定了正交拟合缓和曲线的Levenberg-Marquardt （LM）算法. 同时提出了在寻优过程中，评估当前迭代位置距离最优位置的远近来动态设置LM参数. 最后以一段缓和曲线的实测点为例，随机取样了5 000例初值，采用蒙特卡罗方法对比了GN算法和LM算法拟合缓合曲线的性能. 试验结果表明：GN算法拟合缓合曲线不收敛；对于不同的初始值，LM算法都收敛到相同的最优值，体现了LM算法具有良好的稳健性；LM算法的迭代次数最少为5次，最大为50次，平均为16.8次，迭代次数和初值与最优值位置的远近相关.
- 缓和曲线拟合 /
- 正交最小二乘 /
- Levenberg-Marquardt 算法 /
- Gauss-Newton算法 /
- 最速下降法
Abstract: To identify the parameters of transition curves in as-built alignments by measured points, orthogonal least-squares fitting is studied on the basis of the parameter equation of transition curves. First, eigenvalue analysis has clarified that the Gauss-Newton (GN) algorithm usually fails to converge because of the existence of the ill-condition. Next, a bi-objective optimization model is proposed and the Levenberg-Marquardt (LM) algorithm combining the GN algorithm with the steepest descent method is constructed to fit a transition curve to points orthogonally. The LM parameter is updated dynamically during iterations according to the evaluation of the distance between the current and the optimum locations. Finally, Monte Carlo simulations are employed to test the performances of the GN and LM algorithms with measured points and the same 5 000 initial values. Experimental results show that the GN algorithm diverges while the LM algorithm converges to the same optimum under different initial values. The number of iterations, with an average of 16.8 times and the minimum of 5 times and the maximum of 50 times, is related to the distance between the initial and the optimum locations. The LM algorithm shows a better robustness than the GN algorithm.
- transition curve fitting /
- orthogonal least squares /
- Levenberg-Marquardt algorithm /
- Gauss-Newton algorithm /
- steepest descent method

HTML全文

图 1 缓和曲线正交拟合

Figure 1. Details for transition curve orthogonal fitting

下载: 全尺寸图片幻灯片

图 2 LM算法流程

Figure 2. Flowchart of the LM algorithm

下载: 全尺寸图片幻灯片

图 3 等高线图中的迭代搜索路径

Figure 3. Search paths in contour maps

下载: 全尺寸图片幻灯片

表 1 测量点坐标

Table 1. Coordinates of measured points m

测量点编号	x	y
1	865.463	134.175
2	846.063	149.943
3	826.580	165.608
4	807.136	181.321
5	791.543	193.847
6	771.752	209.123
7	759.529	218.475

下载: 导出CSV

表 2 Gauss-Newton算法迭代过程中的参数和相应指标

Table 2. Parameters and indexes of Gauss-Newton fitting processes

$k$	x_o /m	y_o /m	α/(º)	A/m	${\rm{lg}}\;F $	${\rm{lg}}\left( {\left\\| {{{J}}_k^{\rm{T}}{{r}}\left( {{{{\varTheta}} _k}} \right)} \right\\|} \right)$	${\rm{lg}}\left( {\left\\| {{{{d}}_{k,\;{\rm{L}}}}} \right\\|} \right)$
0	900.000	100.000	140.249	600.000	2.072	3.537	−∞
1	735.480	243.913	142.385	108.016	3.980	4.404	2.898
2	879.610	110.057	176.670	26.008	8.952	8.327	2.763
3	802.088	131.635	176.339	−3.367	7.878	8.138	2.520
4	802.088	155.634	179.746	−4.745	9.416	9.523	1.709
5	775.148	160.986	181.215	−3.605	12.229	12.451	1.803

下载: 导出CSV

表 3 缓和曲线拟合LM算法性能及参数识别统计结果

Table 3. Statistical results of the LM algorithm performance and parameter identification

E(x_o)/m	E(y_o)/m	E(A)/m	E(α)/(º)	E(k)/次		σ(x_o)/mm	σ(y_o)/mm	σ(A)/mm	σ(α)/(″)	σ(k)/次
838.843	155.731	369.277	140.944	16.8		0.001	0.001	0.007	0.010	9.2

下载: 导出CSV

表 4 LM算法迭代过程中的参数和相应指标

Table 4. Parameters and indexes of LM fitting processes

$k$	x_o /m	y_o /m	α/(º)	A/m	${\rm{lg}}\;F$	${\rm{lg}}\left( {\left\\| {{{J}}_k^{\rm{T}}{{r}}\left( {{{{\varTheta}} _k}} \right)} \right\\|} \right)$	$\lg\left( {\left\\| { { {{d} }_{k,\;{\rm{L} } } }} \right\\|} \right)$
0	900.000	100.000	140.249	600.00	2.072	3.537	−∞
1	902.656	103.143	140.258	600.370	−1.216	−1.895	0.618
2	893.401	111.244	140.586	625.124	−1.391	0.825	1.630
3	889.194	114.670	140.635	625.146	−1.519	−0.964	1.186
$\boxed4$	869.025	131.312	140.810	546.664	−1.291	1.530	2.033
4	886.501	116.895	140.664	617.487	−1.528	−0.081	1.097
$\boxed5$	866.523	133.349	140.827	534.455	−1.326	1.488	2.044
5	884.137	118.844	140.684	608.059	−1.536	−0.232	1.107
$\boxed6$	863.879	135.507	140.846	521.855	−1.329	1.474	2.056
6	881.760	120.796	140.703	597.916	−1.546	−0.260	1.126
$\boxed7$	861.167	137.718	140.865	508.737	−1.326	1.462	2.067
7	879.306	122.812	140.722	587.188	−1.557	−0.255	1.146
$\boxed8$	858.414	139.961	140.885	495.097	−1.326	1.446	2.078
8	876.759	124.902	140.742	575.845	−1.567	−0.244	1.167
$\boxed9$	855.641	142.217	140.903	480.977	−1.329	1.425	2.088
9	874.114	127.070	140.762	563.828	−1.582	−0.234	1.188
$\boxed{10}$	852.880	144.460	140.921	466.465	−1.338	1.396	2.095
10	871.363	129.321	140.782	551.071	−1.597	−0.226	1.211
$\boxed{11}$	850.172	146.655	140.938	451.716	−1.355	1.356	2.100
11	868.503	131.659	140.803	537.503	−1.615	−0.221	1.234
12	865.534	134.084	140.824	523.060	−1.634	−0.223	1.257
13	862.459	136.591	140.844	507.692	−1.657	−0.233	1.279
14	859.294	139.168	140.865	491.390	−1.684	−0.257	1.301
15	856.090	141.790	140.884	474.232	−1.714	−0.303	1.318
16	852.847	144.407	140.902	456.449	−1.747	−0.389	1.329
17	839.303	155.394	140.971	379.957	−1.767	0.556	1.959
18	839.639	155.090	140.944	374.792	−1.881	−0.781	0.726
19	838.843	155.731	140.944	369.277	−1.882	−7.307	−2.208

下载: 导出CSV

参考文献(12)

GIBREEL G M, EASA S M, EL-DIMEERY I A. Prediction of operating speed on three-dimensional highway alignments[J]. Journal of Transportation Engineering, 2001, 127(1): 21-30. doi: 10.1061/(ASCE)0733-947X(2001)127:1(21)

BASSANI M, MARINELLI G, PIRAS M. Identification of horizontal circular arc from spatial data sources[J]. Journal of Surveying Engineering, 2016, 142(4): 1-14.

丁克良,欧吉坤,赵春梅. 正交最小二乘法曲线拟合法[J]. 测绘科学,2007,32(3): 18-19. doi: 10.3771/j.issn.1009-2307.2007.03.006

DING Keliang, OU Jikun, ZHAO Chunmei. Methods of the least-squares orthogonal distance fitting[J]. Science of Surveying and Mapping, 2007, 32(3): 18-19. doi: 10.3771/j.issn.1009-2307.2007.03.006

丁克良,刘全利,陈翔. 正交距离圆曲线拟合方法[J]. 测绘科学,2008,33(S1): 72-73.

DING Keliang, LIU Quanli, CHEN Xiang. Fitting of circles based on orthogonal distance[J]. Science of Surveying and Mapping, 2008, 33(S1): 72-73.

AHN S J, RAUH W, WARNECKE H. Least-squares orthogonal distances fitting of circle,sphere,ellipse,hyperbola,and parabola[J]. Pattern Recognition, 2001, 34(12): 2283-2303. doi: 10.1016/S0031-3203(00)00152-7

宋占峰,彭欣,吴清华. 基于中线坐标的地铁调线优化算法[J]. 西南交通大学学报,2014,49(4): 656-661. doi: 10.3969/j.issn.0258-2724.2014.04.015

SONG Zhanfeng, PENG Xin, WU Qinghua. Optimization algorithm for horizontal realignment based on coordinate of metro centerline[J]. Journal of Southwest Jiaotong University, 2014, 49(4): 656-661. doi: 10.3969/j.issn.0258-2724.2014.04.015

DONG H, EASA S M, LI J. Approximate extraction of spiralled horizontal curves from satellite imagery[J]. Journal of Surveying Engineering, 2007, 133(1): 36-40. doi: 10.1061/(ASCE)0733-9453(2007)133:1(36)

LEVENBERG K. A method for the solution of certain non-linear problems in least squares[J]. Quarterly of Applied Mathematics, 1944, 2(2): 164-168. doi: 10.1090/qam/10666

MARQUARDT D W. An algorithm for least-squares estimation of nonlinear parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431-441. doi: 10.1137/0111030

ZHAO R, FAN J. On a new updating rule of the Levenberg-Marquardt parameter[J]. Journal of Scientific Computing, 2018, 74(2): 1146-1162. doi: 10.1007/s10915-017-0488-6

SONG Z, DING H, LI J, et al. Circular curve fitting method for field surveying data with correlated noise[J]. Journal of Surveying Engineering, 2018, 144(4): 1-9.

FAN J, YUAN Y. On the quadratic convergence of the Levenberg-Marquardt method without nonsingularity assumption[J]. Computing, 2005, 74(1): 23-39. doi: 10.1007/s00607-004-0083-1

施引文献

附加材料(0)

访问统计