Modelling of Velocity Pulse-Like Ground Motions Based on Adaptive Matching Algorithm
-
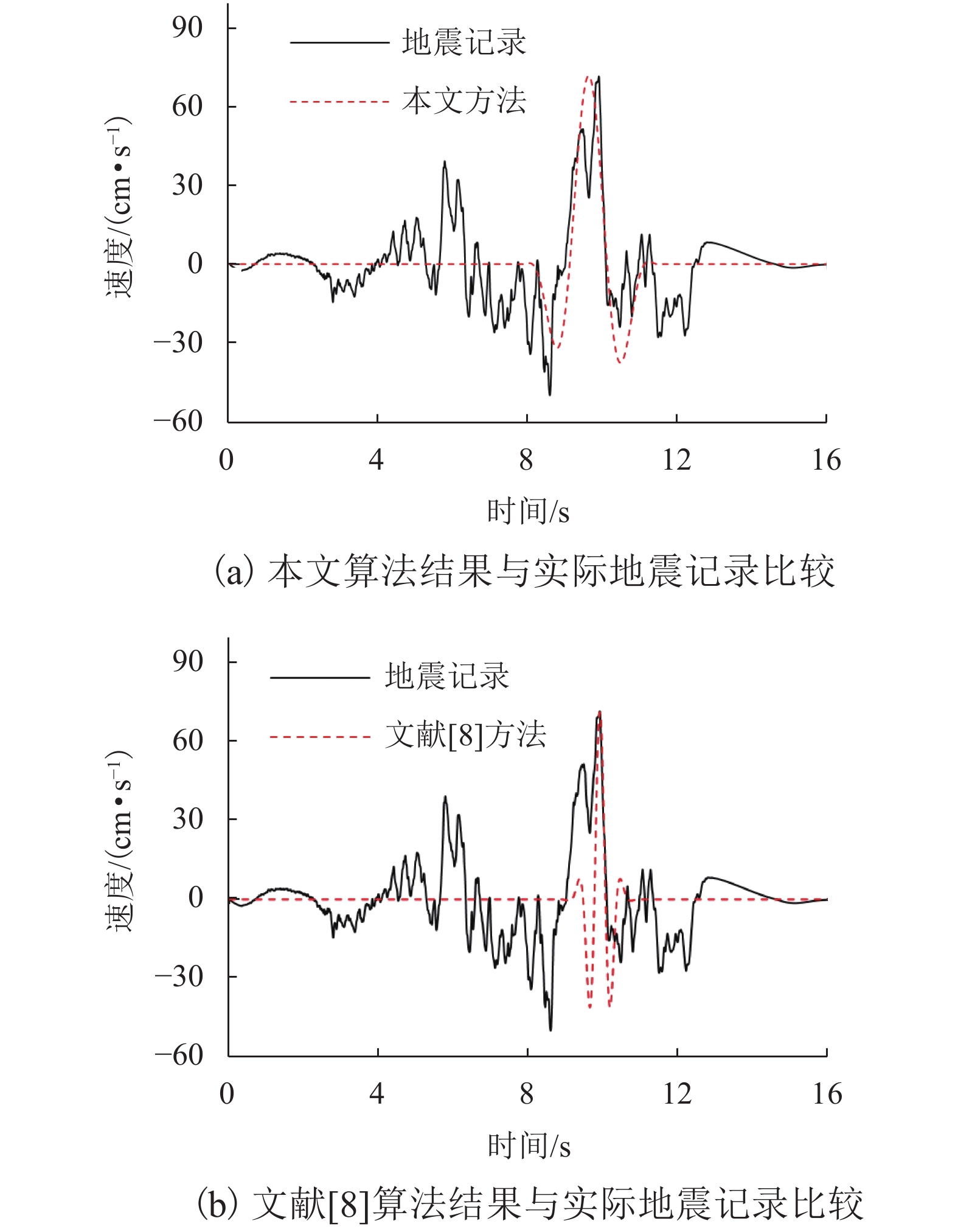
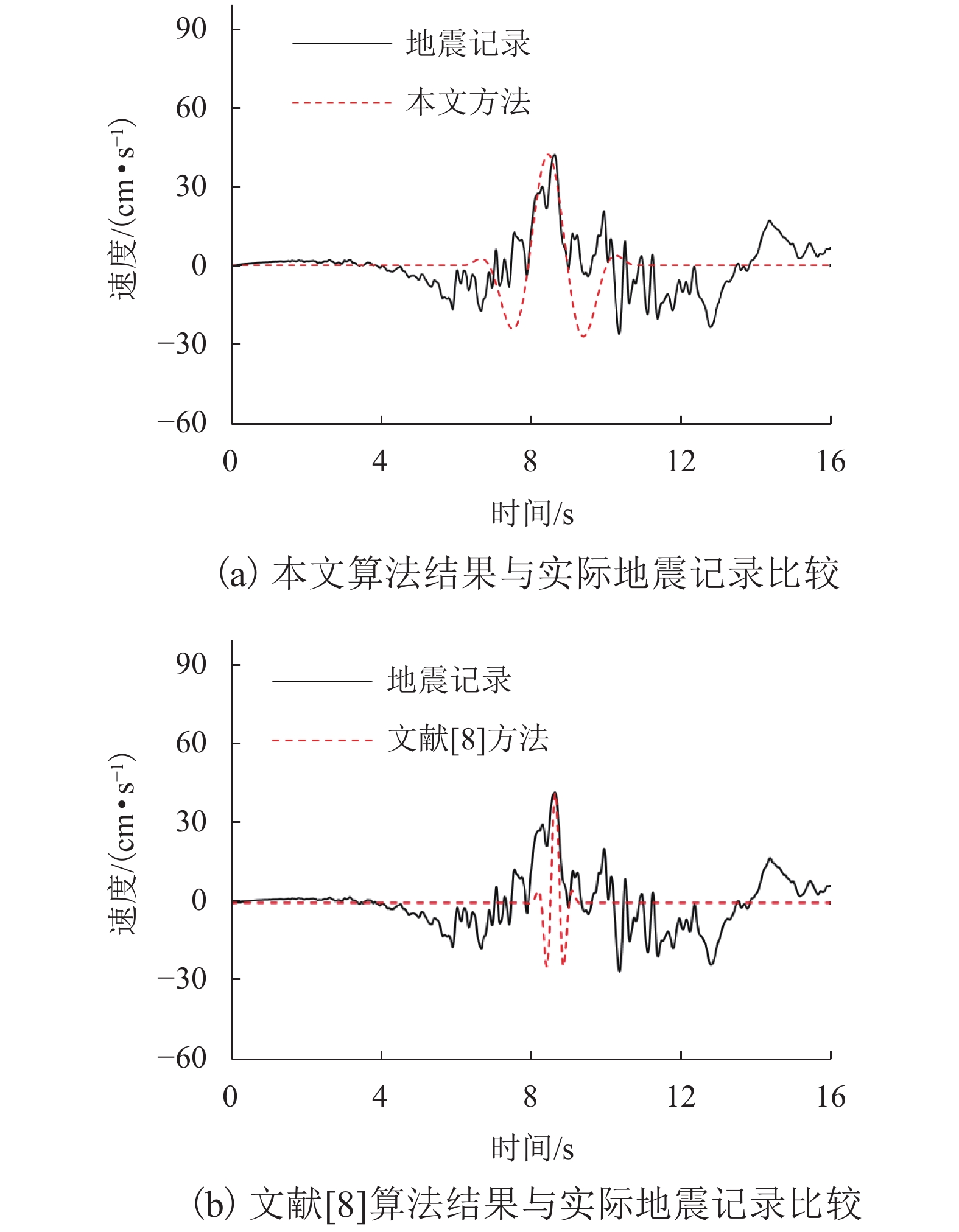
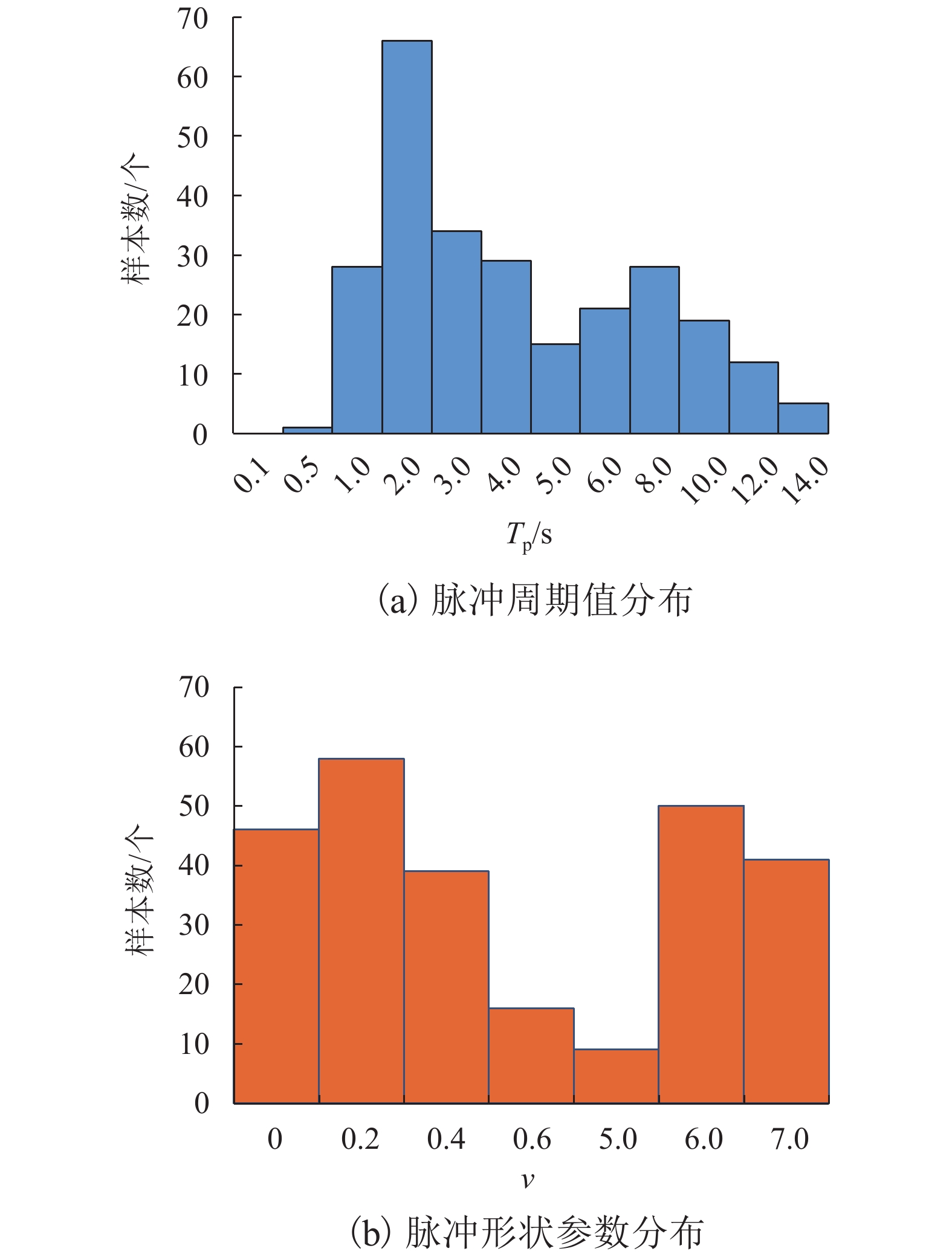
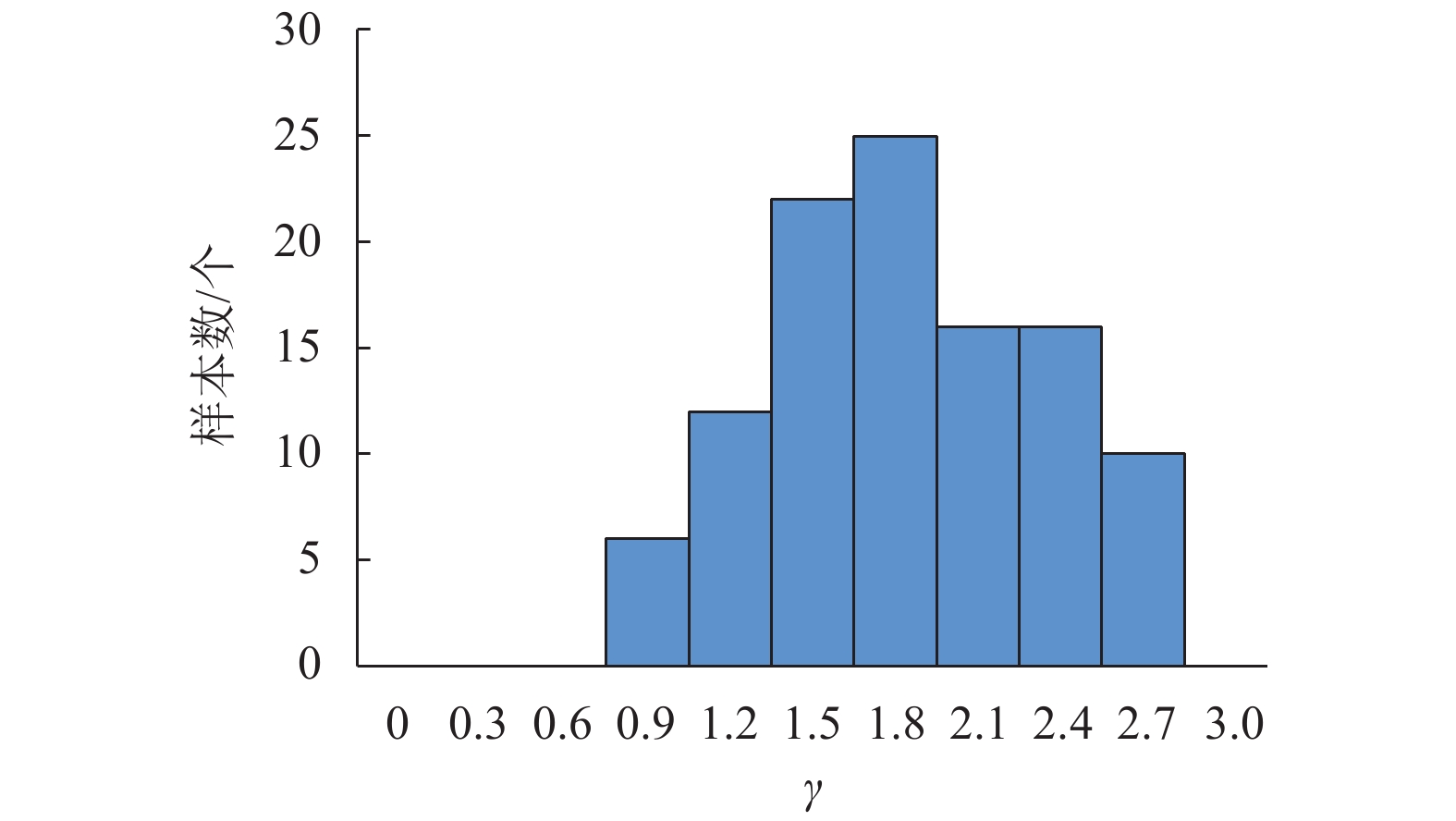
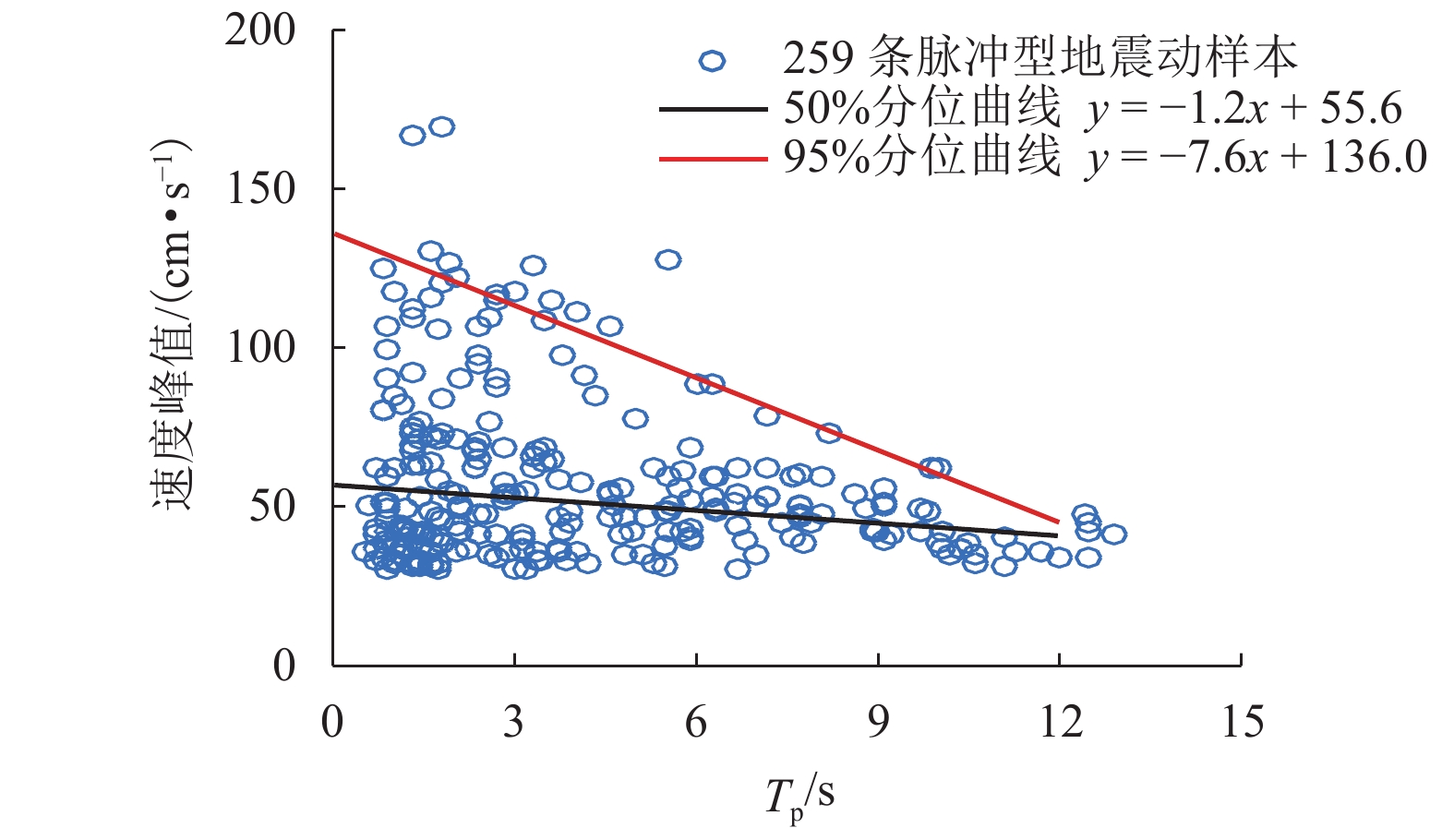
摘要: 速度脉冲型地震记录至今尚未有完整的波形参数识别方法，从地震动数据库中批量识别脉冲记录并搜集波形参数仍然有一定困难. 针对此问题，将脉冲量化识别、脉冲解析函数、自适应匹配算法三者结合，提出一套脉冲波形参数识别方法，可实现脉冲波形和解析函数之间的自适应匹配；该方法包括一个借助EMD (empirical mode decomposition) 的核心算法，对近场速度脉冲型地震记录实现平滑；再以Mavroeidis函数为脉冲基本模型，根据其特征参数的变化范围，分别对脉冲频率、脉冲形状系数、脉冲振荡特征系数进行了参数样本的循环枚举，并由优化算法确定模型参数取值；在此基础上，给出了当前既有的速度脉冲型记录样本的上述模型参数识别结果，并根据统计给出了地面峰值加速度分布和主脉冲周期的关系. 研究结果表明：和既有的方法利用Dickinson模型识别方法相比，本文算法对波形显著不对称的记录主脉冲周期识别错误率降低了约67%，较好的识别稳定性更有利于工程应用.Abstract: Due to the lack of a complete waveform parameter identification method aiming at the velocity pulse-like ground motions up to now, it is still difficult to identify the pulse-like records quantitatively, which hinders definitely collecting the wave shape parameters from ground motion database. In order to solve this problem, a framework for the parameters identification of pulse waveform is presented by combining the pulse quantitative identification and impulsive function analysis with an adaptive matching algorithm to realise the adaptive matching between pulse waveform and the analytic function. As the key part of the framework, the adaptive matching algorithm for parameterizing the pulse waveform is proposed by virtue of the empirical mode decomposition (EMD) in order to smooth the near-fault pulse-like earthquake records. Based on the pulse function given by Marverodis, and within the distribution range of the model parameters, a procedure for parameters adaptive matching is developed, characterized by the enumeration with several loops corresponding to the pulse frequency, pulse shape, and pulse oscillation characteristic respectively. In addition, the least square-based optimization method is applied to determine the final parameters. Using this method, the shape parameters of the main pulses existing in these pulse-like ground motions records were identified. In addition, the relationship between the peak ground velocity and the period of main pulse is drawn from the statistical results. According to the statistical and image analysis, compared with the existing method using the Dickinson model, the algorithm for identifying the main pulse period in this paper can reduce the classification mistake by about 67%. The better stability of near-fault records identification is meaningful to practical engineering applications in seismic design.
-
图 4 速度脉冲型地震记录的脉冲周期和形状参数分布
Figure 4. Distributions of pulse periods and shape parameters for velocity pulse-like ground motions
图 6 速度脉冲型地震动样本P与Tp关系及分位曲线
Figure 6. P-Tp relationship and quantile curves of velocity pulse-like ground motions
表 1 脉冲曲线的解析模型化算法
Table 1. Analytical modelling algorithm of pulse curves
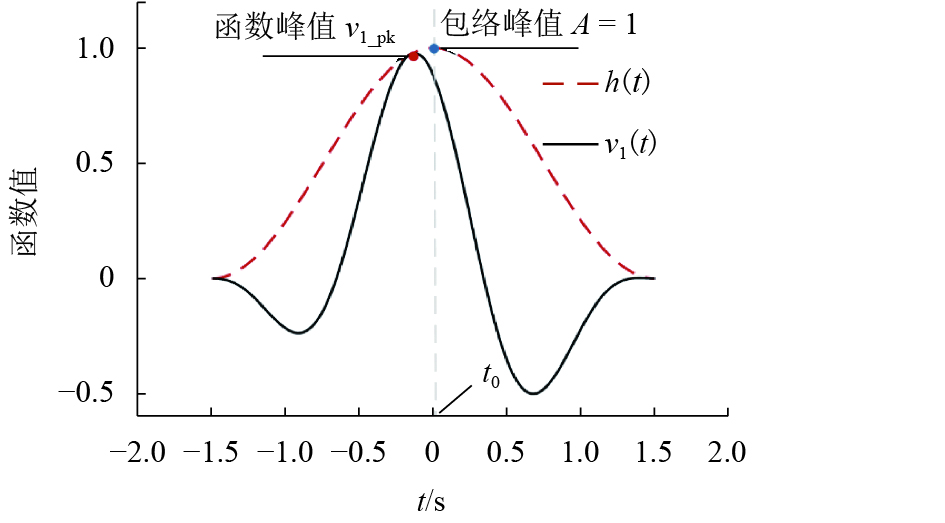
流程编号 计算步骤 （1） 读取速度脉冲型地震记录 S（t）； （2） 用 EMD 方法对主脉冲平滑去噪； （3） 确定 t0，由主脉冲 Xf（t） 峰值点对应的时刻 tpk 代替 t0； （4） 令振动特征参数$\gamma {\rm{ = }}1 $；即单个主脉冲时间段内的穿零率参数； （5） for fj =[f1 : fMAX];对脉冲频率 f 循环； （6） for vi＝[v1:vMAX]; 对脉冲形状参数 v 循环； （7） yij=0.5[1+cos(2πfi(t−t0))][cos(2πf(t−t0)+vi)]；根据算式(7)确定脉冲曲线函数 yij，假定包络幅值曲线等于 1； （8） Aij=P/max{yij}求得对应的 Aij；Yij = yij Aij；以地震记录地位峰值加速度为目标，对脉冲模型调幅； （9） ${D_1}(i，j) = \displaystyle\sum\limits_{t = 0}^n {{{[{{S}}(t){\rm{ - }}{Y_{ij}}(t)]}^2}} $计算${Y_{ij}}$与 S(t) 在单个脉冲周期内的波形误差，并计入 D1(i,j)，n 为时程点数； （10） end for （11） end for （12） [I，J]=find[D1==min(D1)]； %求曲线 Yij 与 v(t) 差异最小的（fi，vj，Aij）组合（fI, vJ, AIJ）； （13） for γk=[γ1: γMAX]；对脉冲振荡特征参数循环 （14） gk=0.5AIJ[1+cos(2πfI(t−t0)/ γk)][cos(2πfI(t−t0)+vJ)]%计算带包络峰值系数 AIJ 的脉冲曲线； （15） ${D_2}(k) = \displaystyle\sum\limits_{t = 0}^n {{{[{{S}}(t){\rm{ - }}{g_k}(t)]}^2}} $
%计算解析模型 gk 与地震记录 v(t) 之间在整个时程上的累计误差，计为 D2(k)；（16） end for （17） K=find[D2==minD2] % 求得与 v(t) 差异最小的曲线 gK，并确定 rK； （18） 存储参数(t0, fI, vJ, AIJ, γK)，并输出 gK 作为脉冲曲线的解析估计结果. 
下载: 导出CSV
-
JONSSON M H, BESSASON B, HAFLIDASON E. Earthquake response of a base-isolated bridge subjected to strong near-fault ground motion[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(6): 447-455. doi: 10.1016/j.soildyn.2010.01.001 ALAVI B, KRAWINKLER H. Behavior of moment-resisting frame structures subjected to near-fault ground motions[J]. Earthquake Engineering & Structural Dynamics, 2010, 33(6): 687-706. CENNAMO C, GESUALDO A, MONACO M. Shear plastic constitutive behavior for near-fault ground motion[J]. Journal of Engineering Mechanics, 2017, 143(9): 241-262. 李明,谢礼立,杨永强,等. 基于反应谱的近断层地震动潜在破坏势研究[J]. 西南交通大学学报,2010,45(3): 331-336. doi: 10.3969/j.issn.0258-2724.2010.03.001LI Ming, XIE Lili, YANG Yongqiang, et al. Potential analysis damage analysis of near fault ground motion based on response spectra[J]. Journal of Southwest Jiaotong University, 2010, 45(3): 331-336. doi: 10.3969/j.issn.0258-2724.2010.03.001 郑史雄,陈志强,陈志伟,等. 近场多脉冲地震作用下高墩桥梁响应分析[J]. 西南交通大学学报,2018,53(3): 104-111.ZHENG Shixiong, CHEN Zhiqiang, CHENG Zhiwei, et al. Seismic response analysis of high-pier bridge under near-fault multiple pulse record exciation[J]. Journal of Southwest Jiaotong University, 2018, 53(3): 104-111. BAKER J W. Quantitative classification of near-fault ground motions using wavelet analysis[J]. Bulletin of the Seismological Society of America, 2007, 97(5): 1486-1501. doi: 10.1785/0120060255 ZHAO G C, LONG-JUN X U, XIE L L. On near-fault ground motion characteristics through multi-scale method[J]. Chinese Journal of Geophysics, 2013, 56(6): 742-753. doi: 10.1002/cjg2.20067 ZHAI Changhai, CHANG Zhiwang, LI Shuang, et al. Quantitative identification of near-fault pulse-like ground motions based on energy[J]. Bulletin of Seismological Society of America, 2013, 103(5): 2591-2603. doi: 10.1785/0120120320 HALL J F, HEATON T H, HALLING M W, et al. Near-source ground motion and its effects on flexible buildings[J]. Earthquake Spectra, 1995, 11(4): 569-605. doi: 10.1193/1.1585828 HE W L, AGRAWAL A K. Analytical model of ground motion pulses for the design and assessment of seismic protective systems[J]. Journal of Structural Engineering, 2008, 134(7): 1177-1188. doi: 10.1061/(ASCE)0733-9445(2008)134:7(1177) TANG Y, ZHANG J. Response spectrum-oriented pulse identification and magnitude scaling of forward directivity pulses in near-fault ground motions[J]. Soil Dynamic and Earthquake Engineering, 2011, 31(1): 59-76. doi: 10.1016/j.soildyn.2010.08.006 DICKINSON B W, GAVIN H P. Parametric statistical generalization of uniform-hazard earthquake ground motions[J]. Journal of Structural Engineering, 2011, 137(3): 410-422. doi: 10.1061/(ASCE)ST.1943-541X.0000330 杨成,唐泽楠,常志旺,等. 基于经验模态分解的速度脉冲型地震动量化识别[J]. 工程力学,2017,34(4): 206-212.YANG Cheng, TANG Zenan, CHANG Zhiwang. EMD-based quantitative categorization for velocity pulse-like ground motions[J]. Engineering Mechanics, 2017, 34(4): 206-212. MAVROEIDIS G P, PAPAGEORGIOU A S. A mathematical representation of near-fault ground motions[J]. Bulletin of the Seismological Society of America, 2003, 93(3): 1099-1130. doi: 10.1785/0120020100 HUANG N E , SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. J. Proc. R. Soc. Lond. A, 1998, 454(3): 903-995. 韩建平,李达文. 基于Hilbert-Huang变换和自然激励技术的模态参数识别[J]. 工程力学,2010,27(8): 54-59.HAN Jianping, LI Dawen. Modal parameter identification based on hilbert-huang transform and natural excitation technique[J]. Engineering Mechanics, 2010, 27(8): 54-59. SHAHI S K, BAKER J W. An empirically calibrated framework for including the effects of near-fault in probabilistic seismic hazard analysis[J]. Bulletin of Seismological Society of America, 2011, 101(2): 742-755. doi: 10.1785/0120100090 VAMVATSIKOS D. Performing incremental dynamic analysis in parallel[J]. Computer and Structures, 2011, 89(2): 170-118. -
下载:
点击查看大图
图(6) / 表(1)
计量
- 文章访问数: 590
- HTML全文浏览量: 281
- PDF下载量: 7
- 被引次数: 0