RC矩形空心墩的新型滞回模型及参数识别方法

黎璟; 邵长江; 钱永久; 杨华平

doi:10.3969/j.issn.0258-2724.20190058

RC矩形空心墩的新型滞回模型及参数识别方法

doi: 10.3969/j.issn.0258-2724.20190058

黎璟^1,,
邵长江¹,
钱永久^1, ,,
杨华平^1,2

基金项目: 国家自然科学基金（51178395）；中国工程院咨询研究项目（2015-05-ZD-002）

详细信息

作者简介:
黎璟（1992—），男，博士研究生，研究方向为桥梁抗震设计理论与方法，E-mail：lijbridge@163.com

通讯作者:
钱永久（1963—），男，教授，博士，研究方向为桥梁抗震设计理论与方法、既有桥梁结构的评估与加固理论、预应力混凝土结构理论以及大跨度混凝土桥梁的设计理论与工程实践等，E-mail：yjqian@sina.com

中图分类号: U442.5
计量
- 文章访问数: 678
- HTML全文浏览量: 487
- PDF下载量: 29
- 被引次数: 0
出版历程
- 收稿日期: 2019-01-04
- 修回日期: 2019-11-04
- 网络出版日期: 2019-12-11
- 刊出日期: 2020-08-01

Innovative Hysteresis Model and Parameter Identification Method for Reinforced Concrete Rectangular Hollow Piers

摘要

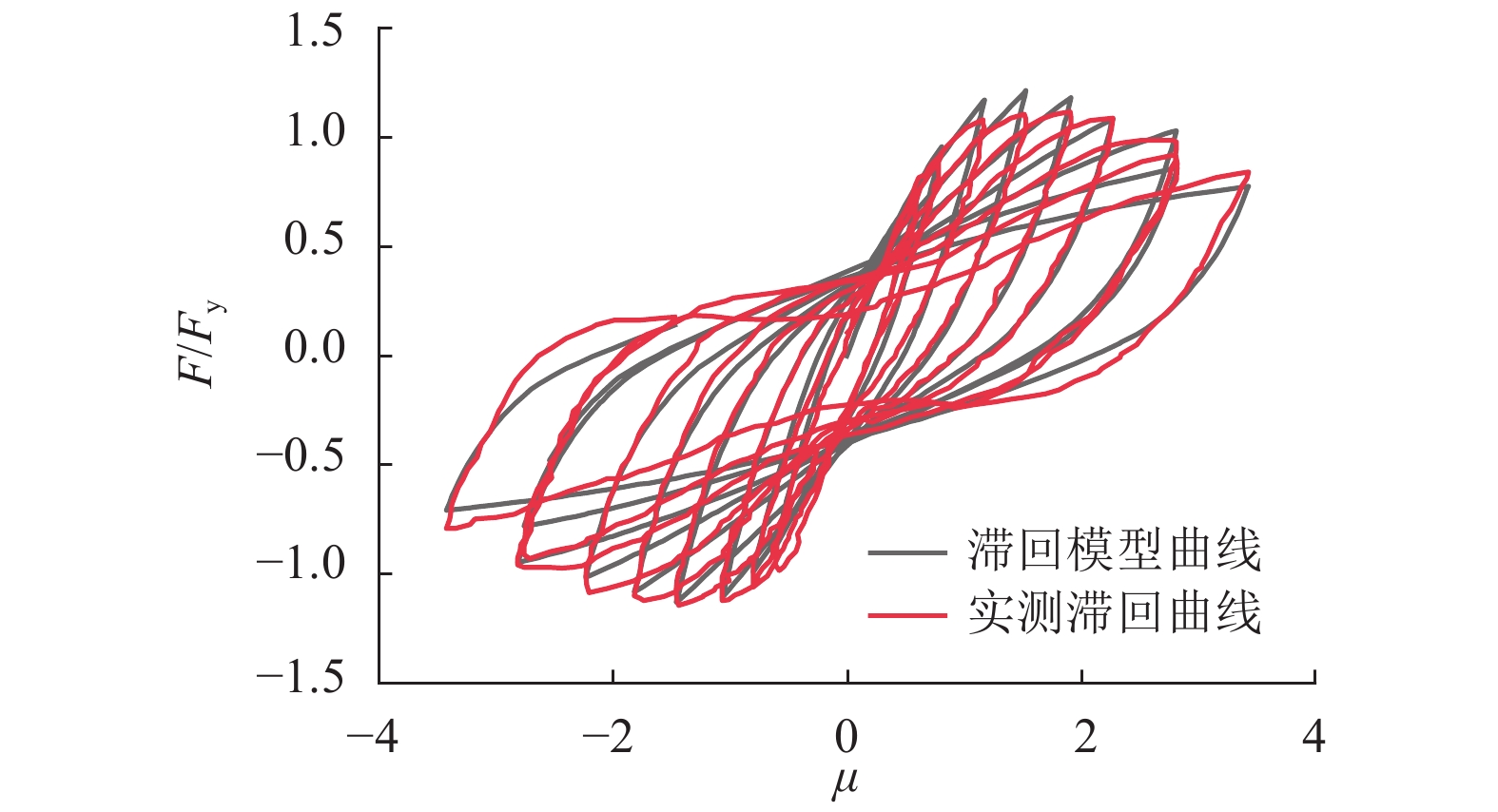
摘要: 为了准确模拟RC （reinforced concrete）矩形空心桥墩的刚度退化特性，为桥梁震后可恢复性能研究提供理论基础，进行了不同设计参数的14个RC矩形空心墩模型拟静力试验. 通过引入峰值位移影响系数体现刚度退化与峰值位移的关联，建立修正的Bouc-Wen-Baber-Noori （BWBN）滞回模型；基于粒子群-引力搜索混合智能优化算法（combination of particle swarm optimization and gravitational search algorithm，PSOGSA）识别实测滞回曲线对应的滞回参数，并建立桥墩设计参数与滞回参数间的对应关系，进而总结滞回参数的经验预测方法. 研究结果表明：修正的BWBN滞回模型曲线与实测滞回曲线吻合程度高，相关性系数在0.98以上，且新型滞回模型能准确地反映出桥墩侧向刚度随墩顶位移退化的特性；PSOGSA算法能精确地识别实测滞回曲线的模型参数；采用经验预测方法得到的模型曲线与实测滞回曲线的相关性系数为0.83，该方法适用于缺乏实测滞回曲线的桥墩.
- 桥梁工程 /
- 抗震设计 /
- RC矩形空心墩 /
- 滞回模型 /
- 智能优化算法
Abstract: In order to precisely simulate the stiffness degradation of RC (reinforced concrete) rectangular hollow piers and provide the theoretical base for the research on post-earthquake resilient bridges, 14 RC rectangular hollow pier specimens with different design parameters were tested under semi-static loading. A modified Bouc-Wen-Baber-Noori (BWBN) hysteresis model was built, in which a peak-displacement coefficient was introduced to reflect the correlation between stiffness degradation and peak displacement. The hysteresis model parameters of each measured hysteresis curve were identified by combination of particle swarm optimization and gravitational search algorithm (PSOGSA). The relationship between the design parameters of hollow piers and hysteresis model parameters were regressed, and an empirical prediction method was summarized. The results show that the modified BWBN hysteresis curve is well matched with the measured hysteresis curve and the correlation coefficients are all above 0.98. The new hysteresis model can reflect how the lateral stiffness of piers degrades with peak displacement. PSOGSA is able to identify the hysteresis model parameters of the measured hysteresis curve precisely. The correlation coefficients between the measured hysteresis curve and modelling curve generated by empirical prediction method is 0.83. The method is applicable to the cases of bridge piers without the measured hysteresis curves.
- bridge engineering /
- seismic design /
- RC rectangle hollow pier /
- hysteresis model /
- intelligent optimization algorithm

HTML全文

图 1 刚度退化指标

Figure 1. Stiffness degradation index

下载: 全尺寸图片幻灯片

图 2 经验预测滞回曲线与实测滞回曲线对比

Figure 2. Comparison of hysteresis mosand measured curve of semi-static specimen

下载: 全尺寸图片幻灯片

表 1 各试件的滞回参数识别结果

Table 1. Identified hysteresis model parameters

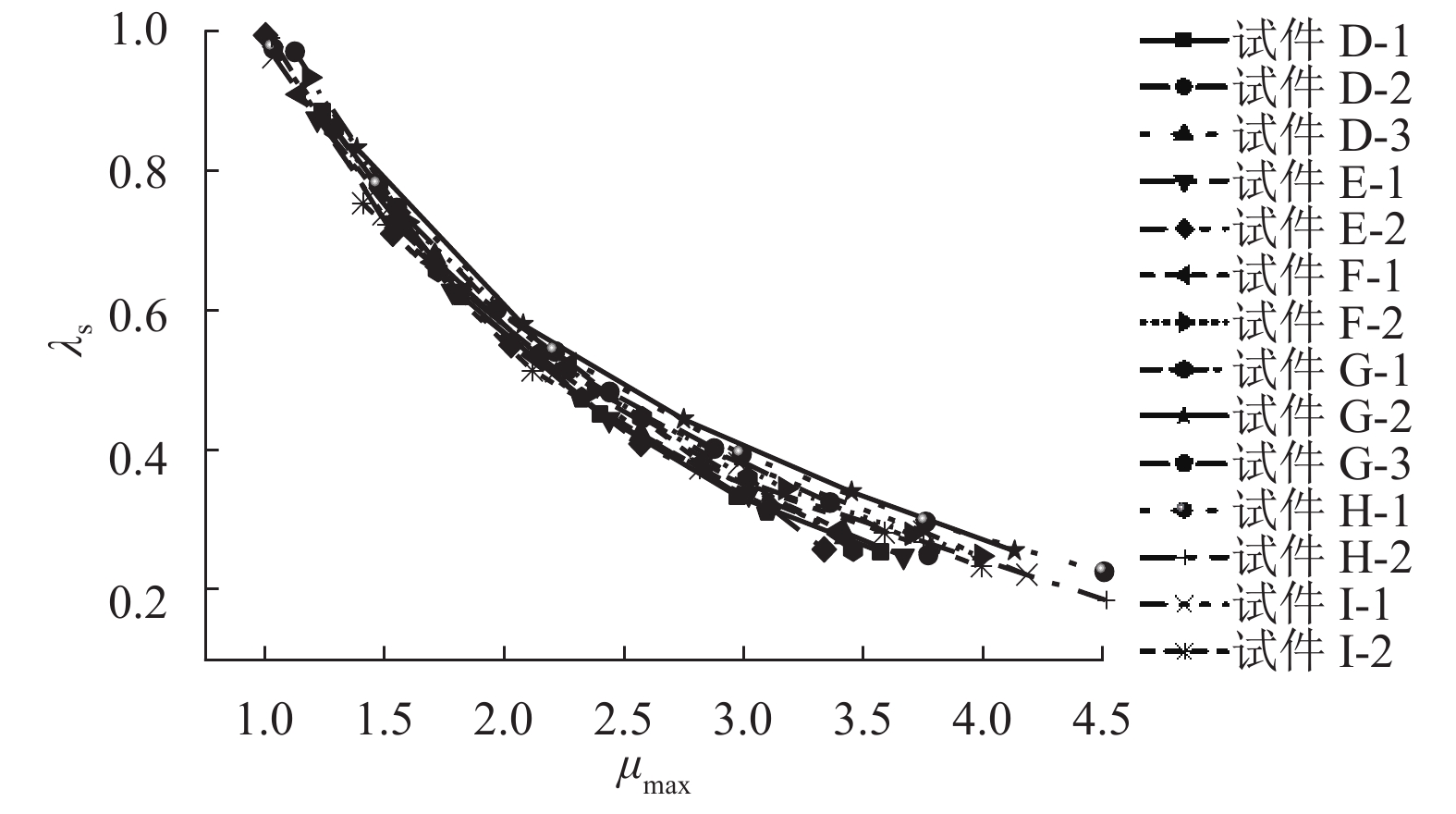
试件编号	ω₀	α	β	γ	n	δ_η / × 10⁻⁵	δ_ν	r	ζ_s	p	q	ψ	δ_ψ / × 10⁻⁴	λ
D-1	1.17	0.07	0.75	−0.06	1.15	1.04	0.08	0.06	0.63	0.46	0.05	0.57	1.58	1.73
D-2	1.03	0.02	0.95	−0.35	0.84	10.80	0.07	0.03	0.72	0.20	0.05	0.58	1.61	2.57
D-3	1.48	0.02	1.36	−0.50	0.94	1.00	0.11	0.11	0.69	0.91	0.05	0.33	1.54	4.68
E-1	1.21	0.06	1.34	−0.26	1.74	1.00	0.11	0.05	0.61	0.71	0.09	0.37	1.54	3.91
E-2	1.34	0.04	0.80	0.01	0.91	1.00	0.05	0.08	0.66	0.63	0.08	0.56	1.56	1.99
F-1	1.48	0.04	1.13	−0.50	1.22	5.51	0.07	0.09	0.64	0.50	0.18	0.40	1.51	4.60
F-2	1.48	0.04	1.21	−0.49	1.73	1.00	0.09	0.10	0.59	0.75	0.14	0.31	1.57	2.80
G-1	1.21	0.02	0.71	−0.40	0.88	1.00	0.08	0.17	0.63	0.59	0.07	0.54	1.50	3.39
G-2	1.13	0.04	0.54	0.12	1.25	21.30	0.09	0.06	0.64	0.50	0.17	0.44	1.23	1.61
G-3	1.37	0.03	1.26	−0.46	1.14	1.09	0.11	0.12	0.66	1.02	0.28	0.35	1.48	3.80
H-1	1.15	0.02	0.59	−0.28	1.50	1.00	0.30	0.15	0.60	0.64	0.18	0.27	1.78	3.64
H-2	1.19	0.02	0.70	−0.34	0.89	24.70	0.15	0.20	0.58	0.62	0.06	0.53	1.48	4.37
I-1	1.25	0.03	0.90	−0.50	0.93	4.92	0.06	0.15	0.61	0.41	0.06	0.62	1.74	2.76
I-2	1.17	0.04	0.85	−0.16	1.24	1.00	0.09	0.06	0.69	0.47	0.05	0.51	1.42	1.83
M-A	1.16	0.05	1.38	−0.34	1.47	4.75	0.12	0.05	0.72	1.03	0.17	0.41	1.15	2.70
M-C	1.07	0.02	0.70	−0.17	2.12	10.90	0.12	0.12	0.67	0.56	0.05	0.70	1.97	1.59

下载: 导出CSV

表 2 相关性系数与误差函数值

Table 2. Correlation coefficient and error function value

试件编号	ρ	E	试件编号	ρ	E	试件编号	ρ	E
D-1	0.989	0.000 7	F-1	0.990	0.000 9	H-1	0.990	0.000 7
D-2	0.991	0.001 1	F-2	0.991	0.000 7	H-2	0.992	0.000 7
D-3	0.992	0.000 9	G-1	0.986	0.001 0	I-1	0.992	0.000 8
E-1	0.994	0.000 8	G-2	0.992	0.000 8	I-2	0.994	0.000 7
E-2	0.992	0.001 0	G-3	0.992	0.001 0	M-A	0.986	0.003 6
						M-C	0.987	0.002 9

下载: 导出CSV

表 3 桥墩设计参数与滞回参数对应关系的经验系数值

Table 3. Empirical coefficient of relationship between design parameters and hysteresis model parameters

滞回参数	x₁	x₂	x₃	x₄	x₅	x₆	x₇	x₈
ω₀	−0.248	−0.268	0.101	−0.678	−0.102	−0.093	−0.058	1.103
α	−0.993	−2.600	−0.172	−5.049	0.372	0.298	0.122	−2.473
β	−0.524	−5.445	0.169	−3.676	0.000	0.150	0.116	−0.051
γ	−0.310	−16.783	0.261	−2.943	−1.211	0.202	−0.265	5.768
n	−0.436	−5.623	0.003	1.451	0.412	0.424	0.090	−0.397
δ_η	0.428	−0.878	−0.993	0.788	−0.969	−0.883	−0.213	−0.893
δ_ν	0.194	19.570	0.086	−1.908	0.212	1.000	0.838	−16.067
r	1.151	0.725	−0.035	5.272	−0.519	−0.266	−0.304	−0.305
ζ_s	−0.043	1.485	0.018	−0.443	0.071	−0.016	0.071	−1.447
p	−0.022	−4.656	0.220	−3.524	0.187	0.068	0.217	−2.569
q	0.618	5.006	0.316	−7.662	−0.093	0.475	0.624	−10.946
ψ	0.245	−19.424	−0.114	4.005	−0.307	−0.340	−0.607	9.579
λ	−0.226	−3.248	0.150	−2.645	−0.423	0.160	−0.031	2.237

下载: 导出CSV

表 4 拟静力试验的设计参数

Table 4. Design parameters of semi-static specimen

参数	b₁/mm	b₂/mm	d//mm	h/mm	n₀
值	360	360	100	1 600	0.1

参数	ρ₀/%	ρ_v/%	f_y/MPa		f_c/MPa
值	1.4	0.72	335		38.7

下载: 导出CSV

表 5 经验预测滞回参数

Table 5. Identified hysteresis model parameters ofsemi-static specimen

参数	ω₀	α	β	γ	n	δ_η
值	1.25	0.03	0.55	−0.11	0.56	1.18 × 10⁻⁴

参数	δ_ν	r	ζ_s	p	q	ψ	λ
值	0.14	0.12	0.71	0.34	0.07	0.2	2.15

下载: 导出CSV

参考文献(19)

李建中,管仲国. 桥梁抗震设计理论发展: 从结构抗震减震到震后可恢复设计[J]. 中国公路学报,2017(12): 1-9,59. doi: 10.3969/j.issn.1001-7372.2017.12.001

LI Jianzhong, GUAN Zhongguo. Research progress on bridge seismic design:target from seismic alleviation to post-earthquake structural resilience[J]. China Journal of Highway and Transport, 2017(12): 1-9,59. doi: 10.3969/j.issn.1001-7372.2017.12.001

余波,宁超列. 工程结构非弹性地震动力反应分析的BWBN模型[J]. 工程力学,2017(增刊1): 252-262.

YU Bo, NING Chaolie. Recent progress on BWBN model for structural inelastic seismic response analy-sis[J]. Engineering Mechanics, 2017(S1): 252-262.

VELETSOS A S, NEWMARK N M, CHELAPATI C V. Deformation spectra for elastic and elastoplastic systems subjected to ground shock and earthquake motions[C]//Proceedings of the 3rd World Conference on Earthquake Engineering. Auckland: Earthquake Engineering Research Institute, 1965: 663-682.

CLOUGH R W, JOHNSTON S B. Effect of stiffness degradation on earthquake ductility requirements[M]. [S.l.]: University of California, 1966: 227-232.

TAKEDA T, SOZEN M A, NIELSON N N. Reinforced concrete response to simulated earth-quakes[J]. Journal of the Structural Division, 1970, 96(12): 2557-2573.

IBARRA L F, MEDINA R A, KRAWINKLER H. Hysteretic models that incorporate strength and stiffness deterioration[J]. Earthquake Engineering & Structural Dynamics, 2005, 34(12): 1489-1511.

BOUC R. Forced vibration of mechanical systems with hysteresis[C]//Proceedings of the Fourth Conference on Nonlinear Oscillation. Prague: [s.n.], 1967: 315-318.

WEN Y K. Method for random vibration of hysteretic systems[J]. Journal of Engineering Mechanics. ASCE, 1989, 102(2): 249-263.

BABER T T, WEN Y K. Random vibrations of hysteretic degrading systems[J]. Journal of Engineering Mechanics, 1981, 107(6): 1069-1089.

BABER T T, NOORI M N. Random vibration of degrading pinching systems[J]. Journal of Engineering Mechanics, 1985, 111(8): 1010-1026. doi: 10.1061/(ASCE)0733-9399(1985)111:8(1010)

KUNNATH S K, MANDER J B, FANG L. Parameter identification for degrading and pinched hysteretic structural concrete systems[J]. Engineering Structures, 1997, 19(3): 224-232. doi: 10.1016/S0141-0296(96)00058-2

韩强,董慧慧,郭婕. 考虑强度和刚度退化及捏拢效应的钢筋混凝土桥墩滞回模型及其参数识别[J]. 振动工程学报,2015(3): 381-393.

HAN Qiang, DONG Huihui, GUO Jie. Hysteresis model and parameter identification of RC bridge piers considering strength and stiffness degradation and pinching effect[J]. Journal of Vibration Engineering, 2015(3): 381-393.

余波,李长晋,吴然立. 钢筋混凝土柱的非弹性恢复力模型与参数识别[J]. 振动与冲击,2016(21): 229-235.

YU Bo, LI Changjin, WU Ranli. Inelastic restoring force model and its parametric identification for reinforced concrete columns[J]. Journal of Vibration and Shock, 2016(21): 229-235.

余波,李长晋,吴然立. 钢筋混凝土柱的非对称恢复力模型与参数识别[J]. 工程力学,2017(2): 153-161.

YU Bo, LI Changjin, WU Ranli. Asymmetric restoring force model and parameter identification of reinforced concrete column[J]. Engineering Mechanics, 2017(2): 153-161.

CALVI G M, PAVESE A, RASULO A, et al. Experimental and numerical studies on the seismic response of RC hollow bridge piers[J]. Bulletin of Earthquake Engineering, 2005, 3(3): 267-297. doi: 10.1007/s10518-005-2240-0

MIRJALILI S, HASHIM S Z M. A new hybrid PSOGSA algorithm for function optimizaion[C]//Inte-rnattional Conference on Computer and Information Application. Tianjin: [s.n.], 2010: 374-377.

MANDER J B, PRIESTLEY M J N, PARK R. Behavior of ductile hollow reinforced concrete colu-mns[J]. New Zealand National Society for Earthquake Engineering, 1983, 16(4): 273-290.

SENGUPTA P, LI Bing. Modified Bouc-Wen model for hysteresis behavior of RC beam-column joints with limited transverse reinforcement[J]. Engineering Struc-tures, 2012, 46(2): 392-406.

ZHANG Yuye, HARRIES K A, YUAN Wancheng. Experimental and numerical investigation of the seismic performance of hollow rectangular bridge piers constructed with and without steel fiber reinforced conc-rete[J]. Engineering Structures, 2013, 48(1): 255-265.

施引文献

附加材料(0)

访问统计