Effect of Brace-to-Chord Angle on Performance of Unstiffened Circular Hollow Section X-Joints under Brace Axial Force
-
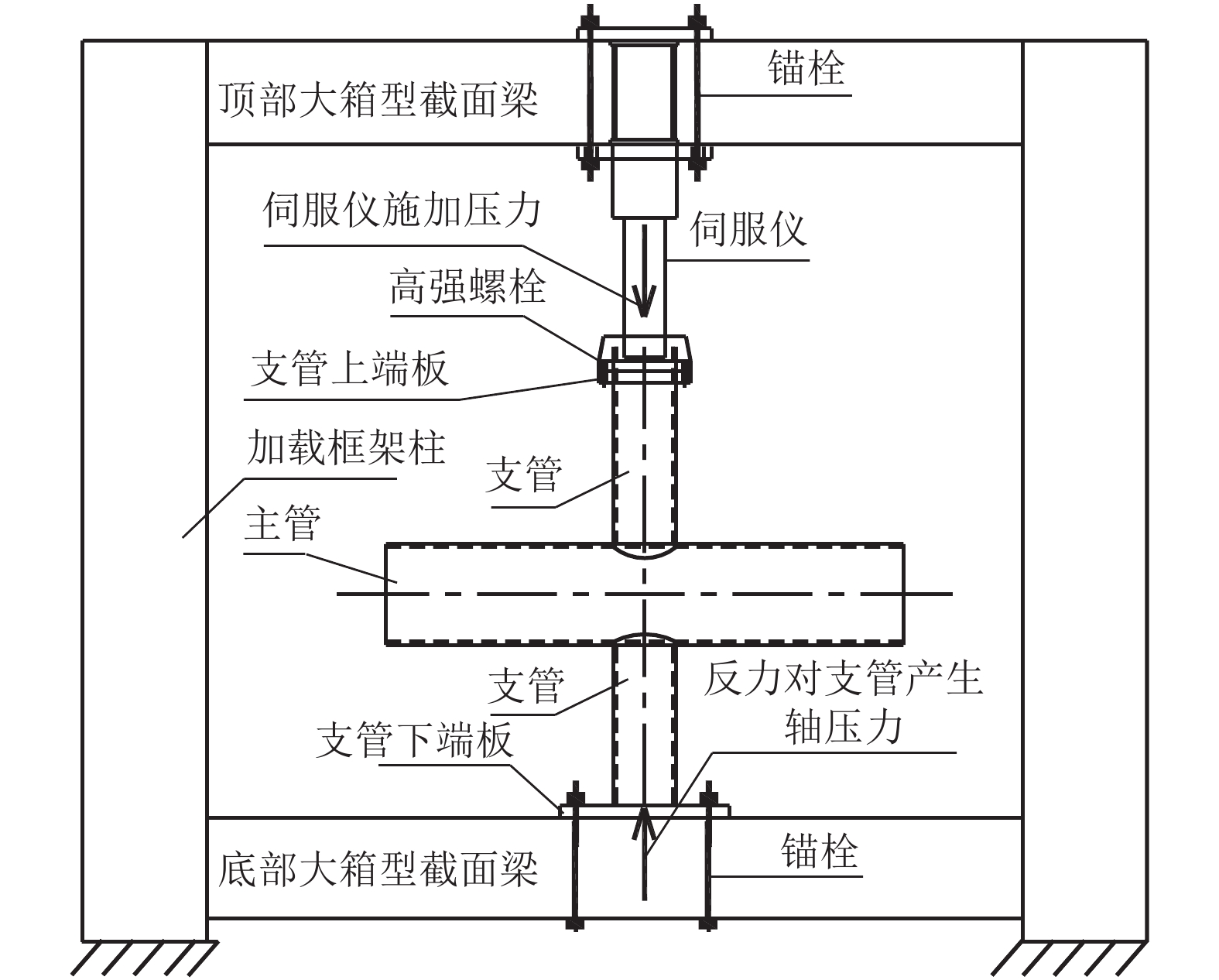
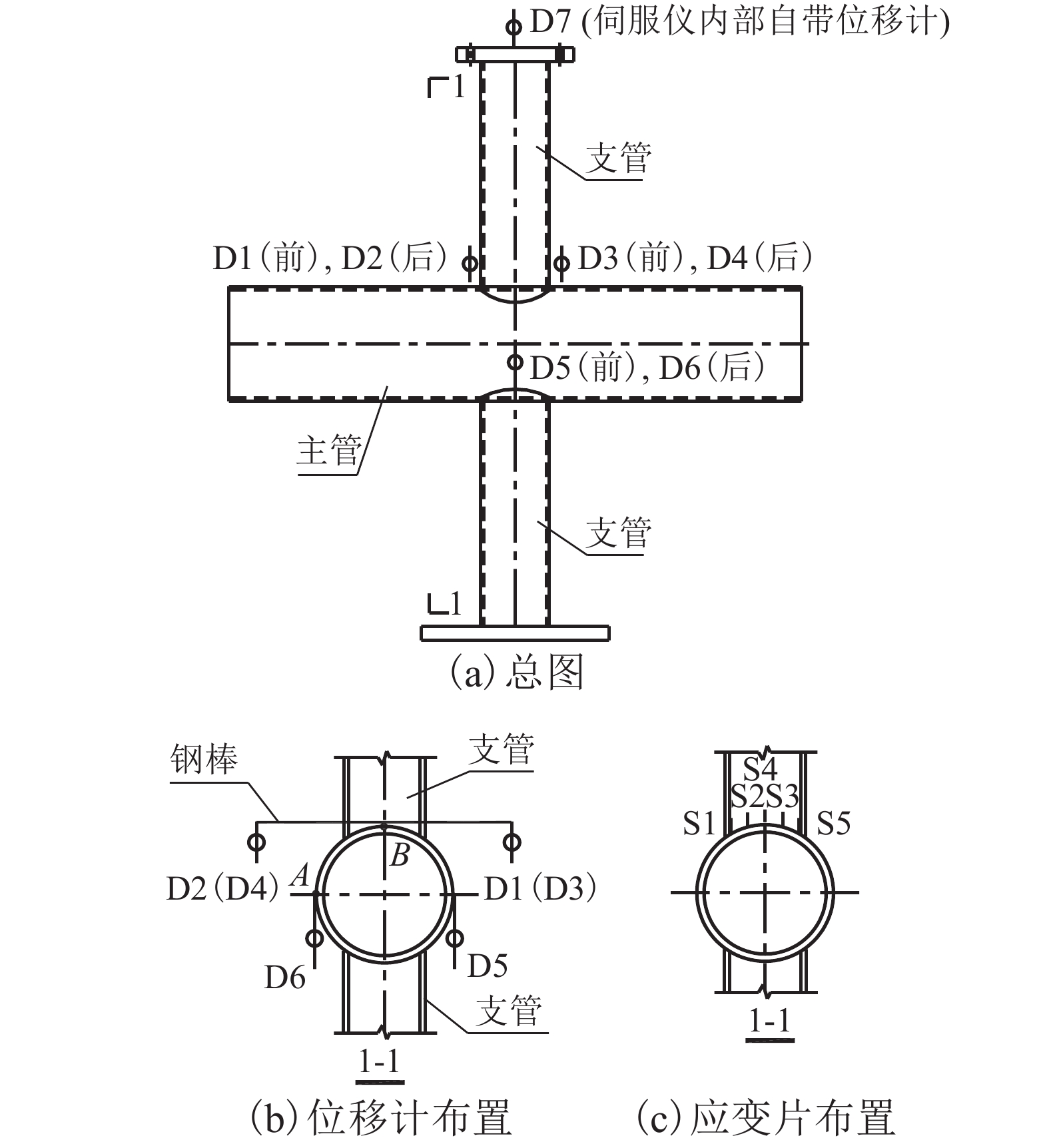
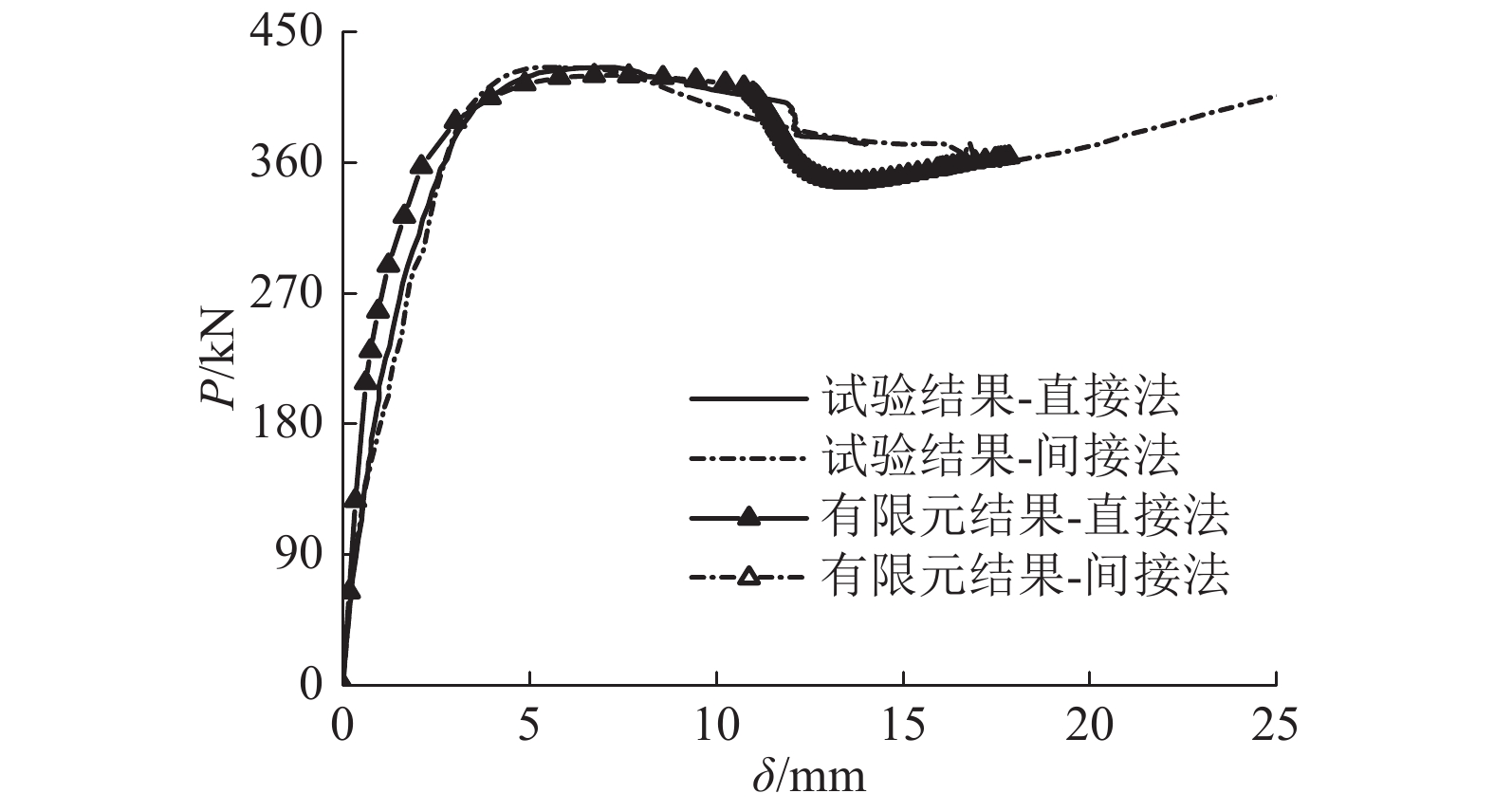
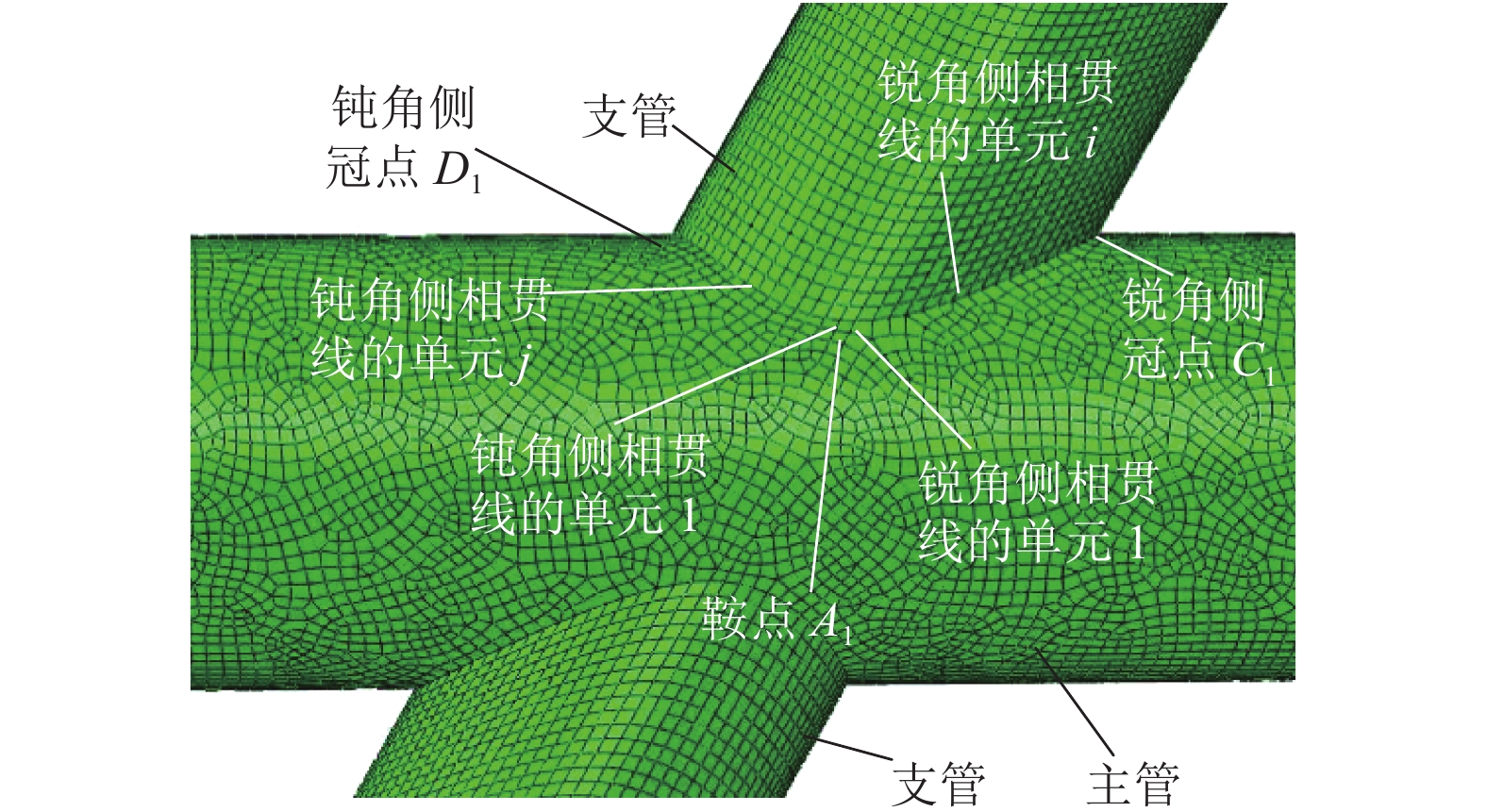
摘要: 为了研究支主管夹角对X形圆钢管相贯节点轴向受力性能的影响，进行相关试验来校验有限元模型，以有限元为手段分析了支主管夹角对X形节点在支管轴力作用下的传力特性和承载力的影响；根据有限元参数分析结果，对支主管夹角较小的节点的承载力提出了改进建议. 研究结果表明：节点试件的破坏模式为相贯线附近主管管壁局部屈曲；当支主管非正交但夹角大于60° 时，节点的传力特性与支主管正交节点的相近，符合Togo模型的假定，现行规范中的夹角正弦的倒数项能精准地反映夹角对节点承载力的影响；但当节点的支主管夹角小于45° 时，其传力特性与Togo模型的假定有较大的差异，夹角正弦的倒数也低估了支主管夹角对节点承载力的提高，对于夹角接近30° 的节点甚至低估了30%；因此建议当夹角小于45° 时，在规范已有的节点承载力计算式的基础上乘以修正系数.Abstract: In order to study the effect of brace-to-chord angle (BCA) on the performance of unstiffened circular hollow section (CHS) X-joints under brace axial force, experimental test was carried out to verified finite element (FE) model. Then FE parameter analysis were used to study the effect of BCA on the stress transfer and bearing capacity of the X-joints under brace axial force, and the capacity prediction accuracy of the X-joints with small BCA was improved. The results show that the failure pattern of test is local buckling of chord wall near brace-to-chord intersection. The incline X-joints (brace-to-chord non-orthogonal) with BCA greater than 60° have the similar stress transfer characteristic to that of the brace-to-chord orthogonal X-joints, which is consistent with the assumption of the Togo model. Moreover, the reciprocal of the sine of BCA (RSBCA) in the current specification can accurately reflect the influence of BCA on the capacity. However, the stress transfer characteristics of the incline X-joints with BCA less than 45° are quite different from the assumption of the Togo model, and RSBCA underestimates the beneficial effect of BCA on the capacity of these X-joints (even 30% for the X-joint with BCA near to 30°). Hence, it is recommended to multiply a correction coefficient on the existing capacity prediction formula of these CHS X-joints with BCA less than 45°, to improve the prediction accuracy.
-
石材幕墙面板背栓式连接是石材幕墙的一种常见施工方法，采用背栓式连接的石材幕墙抗震性能力强[1-3]，稳定性能高[4-6]，施工强度低，机械化施工程度高，安装方便灵活. 石材幕墙连接节点的破坏占很大比例[7-8]，另外高温、湿度的变化都会导致石材强度下降[9]. 石材经风化后，承载力下降明显，石材幕墙面板常有断裂情况出现[10-11]，因此保证石材幕墙面板断裂后的整体性是提高面板安全性的重要措施. 目前，国内外关于石材幕墙面板加固和高空防坠措施的研究相对较少.
本文对33块背栓式石材面板进行了抗弯试验，并对其抗弯承载力进行了分析，研究了石材面板的加固和防高空坠落措施，为背栓式石材幕墙面板工程应用提供参考.
1. 试验概况
1.1 试件设计
石材面板为尺寸600 mm × 400 mm × 30 mm的花岗岩. 背栓采用慧鱼敲击式背栓，节点加固用不锈钢金属圆环，金属圆环厚度2 mm，金属圆环半径40 mm. 石材面板尺寸及加工方案见图1，试件的参数变化见表1. 试件编号中，BS、J、F、B分别表示背栓式石材面板、节点加固、迎风面加载、背风面加载，1、2、3、4分别代表GFRP （glass fiber reinforced plastics）布采用十字、对角、纵向全贴和横向全贴的加固方式. 所用石材均为同一批次黄金麻花岗岩.
考虑正负风压的作用，对石材面板进行了迎风面和背风面加载方向的试验，加载速度为0.5 mm/min，当荷载降至峰值荷载85%时停止加载，加载装置及测量方案如图2所示.
表 1 试件设计参数Table 1. Details of specimens试件编号 数量/个 厚度/mm 连接节点 GFRP 粘贴方式 试件编号 数量/个 厚度/mm 连接节点 GFRP 粘贴方式 BS-F 3 30 BS-B 3 30 BS-J-F 3 30 加固 BS-J-B 3 30 加固 BS-J-F-1 3 30 加固 十字 BS-J-B-1 3 30 加固 十字 BS-J-F-2 3 30 加固 对角 BS-J-B-2 3 30 加固 对角 BS-J-F-3 3 30 加固 纵向全贴 BS-J-B-3 3 30 加固 纵向全贴 BS-J-F-4 3 30 加固 横向全贴 1.2 材料性能
黄金麻花岗岩的实测弯曲强度为4.14 MPa. GFRP的实测性能如表2所示.
表 2 GFRP实测性能Table 2. Measured performance of GFRP试样 抗拉强度/MPa 厚度/mm 弹性模量/MPa GFRP 1 444.4 0.167 1.33 × 105 2. 试验结果
2.1 试验现象及破坏形态
在迎风面荷载作用下，石材面板标准件和节点加固的面板破坏时发出轻微的断裂声，面板断裂严重，承载力迅速下降，破坏非常突然. 背面采用GFRP十字粘贴和对角粘贴的石材幕墙面板，石材面板主要产生纵向贯通裂缝，加载过程中有GFRP的撕裂声，石材面板开裂后承载力缓慢下降，GFRP与断裂石材表面逐渐出现滑脱，破坏过程缓慢. 背面采用GFRP纵向和横向全贴的石材幕墙面板，破坏过程相似，分别出现纵向和横向贯通裂纹，承载力下降缓慢. 其破坏形态如图3（a）~（f）所示.
在背风面荷载的作用下，未进行加固的石材面板在背栓处产生了拉拔破坏现象，节点加固后的石材面板背栓孔处未发生破坏，说明采用金属圆环对石材面板连接节点进行加固是有效的. 背面采用GFRP加固的石材面板断裂后无碎块掉落，断裂石材与GFRP粘接完好，能保证一定的整体性. 其破坏形态如图3（g）~（k）所示.
2.2 试验结果与分析
不同试件极限荷载的柱状图如图4所示. 石材幕墙面板在不同荷载下的试验结果见表3所示，其中(1)、(2)、(3)表示在3次不同荷载下的试验.
表 3 不同荷载下试验结果Table 3. Test results under different loadings试件编号 试验 极限荷载/N 极限位移/mm 破坏形态 试件编号 试验 极限荷载/N 极限位移/mm 破坏形态 BS-F (1) 20.530 1.12 节点破坏 BS-B (1) 9.423 1.29 节点破坏 (2) 21.873 0.91 (2) 9.603 1.22 (3) 20.794 1.05 (3) 9.279 1.19 平均荷载 21.065 1.03 平均荷载 9.435 1.23 BS-J-F (1) 23.676 1.18 板断裂 BS-J-B (1) 14.051 1.91 板断裂 (2) 23.245 1.26 (2) 13.946 1.94 (3) 24.152 1.22 (3) 14.513 2.08 平均荷载 23.691 1.22 平均荷载 14.170 1.98 BS-J-F-1 (1) 69.533 5.03 板断裂 BS-J-B-1 (1) 14.867 1.63 板断裂 (2) 70.463 4.97 (2) 14.513 1.45 (3) 68.987 4.85 (3) 14.725 1.53 平均荷载 69.661 4.95 平均荷载 14.702 1.54 BS-J-F-2 (1) 58.765 4.22 板断裂 BS-J-B-2 (1) 16.478 1.32 板断裂 (2) 57.360 4.13 (2) 16.344 1.51 (3) 57.553 4.24 (3) 15.681 1.45 平均荷载 57.893 4.20 平均荷载 16.168 1.43 BS-J-F-3 (1) 31.113 1.43 板断裂 BS-J-B-3 (1) 14.862 1.29 板断裂 (2) 38.031 1.52 (2) 15.577 1.36 (3) 36.145 1.48 (3) 15.245 1.45 平均荷载 35.096 1.48 平均荷载 15.227 1.37 BS-J-F-4 (1) 56.975 2.71 板断裂 (2) 60.895 2.77 平均荷载 58.935 2.74 由表3可以看出：在迎风面加载作用下，背面采用十字、对角、纵向全贴和横向全贴GFRP进行加固石材面板，极限承载力分别是未加固石材面板的3.30倍、2.75倍、1.74倍和2.80倍. 试验采用的GFRP是单向编制的，GFRP粘贴方向对加固石材面板的极限承载力和破坏形态有一定影响. 两种全贴GFRP的加固方式下，石材断裂裂纹都出现在与纤维平行的方向，都没能充分发挥GFRP的强度.
在背风面加载条件下，节点加固石材面板的承载力是未加固试件的1.50倍，均为脆性破坏. 石材面板背面粘贴GFRP后，虽然承载力无明显提高，但是石材面板破坏后能保持整体性.
3. 有限元分析
3.1 有限元模拟校核
为了分析GFRP加固背栓式石材面板的受力过程，采用Abacus有限元软件对极限荷载进行了模拟. 将石材定为线弹性材料，采用最大主拉应力破坏准模拟开裂. 石材性能取实测性能，参考高强混凝土开裂应变经验值为1 × 10−4 [12]，石材的开裂应变取相同值. 石材实体单元用C3D8R减缩积分进行模拟，为了限制“沙漏”的扩展，直接选用enhanced方式控制沙漏.
假定纤维方向GFRP应力-应变关系为线弹性，用S4R壳单元来模拟. 材料本构关系和有限元本构模型分别如图5和图6所示. 图5中：σ和ε分别为石材的应力和应变；σu和εu分别为石材的极限压应力和极限压应变；σfe和εfe分别为GFRP的有效拉应力和有效拉应变. 石材面板与钢垫板设置表面与表面接触，接触属性定义为默认属性. 背栓与背栓孔的相互作用采用铰接约束.
模拟的结果与试验值进行对比如表4所示. 由表4可以看出，所建立的有限元模型基本正确，极限强度的误差在15.00%以内，可以用来分析GFRP加固石材幕墙面板的抗弯性能.
表 4 荷载模拟值与试验值对比Table 4. Comparison of simulated and experimental values试件编号 试验值/N 模拟值/N 误差/% BS-B 9 435.45 9 965.11 5.61 BS-J-B 14 170.55 15 383.55 8.56 BS-J-B-1 14 702.06 15 957.79 8.54 BS-J-B-2 16 168.12 17 680.88 9.36 BS-J-B-3 15 227.31 13 246.92 13.01 BS-F 21 065.81 23 706.66 12.54 BS-J-F-1 69 661.34 78 417.77 12.57 BS-J-F-2 57 893.21 64 527.76 11.46 BS-J-F-3 35 096.88 38 880.32 10.78 3.2 初始安装缺陷分析
背栓成孔质量对石材面板的受力有很大影响. 采用有限元模型可以分析背栓的初始安装缺陷对承载力的影响. 当背栓安装不合格时，认为该背栓不参与石材面板受力，其分析结果如表5所示.
表 5 初始安装缺陷分析Table 5. Initial installation defect analysis石材
编号缺陷数/个 极限荷载/N 试验荷载/N 降低率/% BS-B 1 6 382.3 9 435.0 32.36 BS-B 2 （对角） 4 229.7 9 435.0 55.17 由表5可以看出，背栓质量出现问题后，对背栓承载力影响很大，一个背栓开孔质量不合格，承载力下降约32.36%，出现两个不合格，则承载力下降达55.17%.
4. 结 论
1） 采用金属圆环对连接节点进行加固，对石材面板连接节点的承载力有明显的提高作用，相对于未加固的石材面板，承载力提高0.50倍.
2） 石材面板背面粘贴GFRP的3种加固方式，都能较好地保证石材面板破坏后的整体性，并能提高石材面板迎风面加载方向的抗弯承载力，十字粘贴效果较好，承载力提高2.30倍. 考虑到承载力的提高率以及材料用量的经济性，十字粘贴效果最好.
3） 有限元模型可以用来计算石材面板的承载力抗弯强度，计算误差在15.00%以内.
-
图 5 有限元和试验所得轴力-局部变形对比
Figure 5. Brace compression-local deformation comparison between test and FE results
图 7 支主管夹角对节点传力的影响
Figure 7. Effect of brace-to-chord angel on the load transfer under brace axial force
图 9 支主管非正交对节点轴压承载力的影响
Figure 9. Effect of brace-to-chord non-perpendicularity on the capacity of CHS X-joints under brace compression
表 1 试件的几何特征
Table 1. Geometry of the specimen
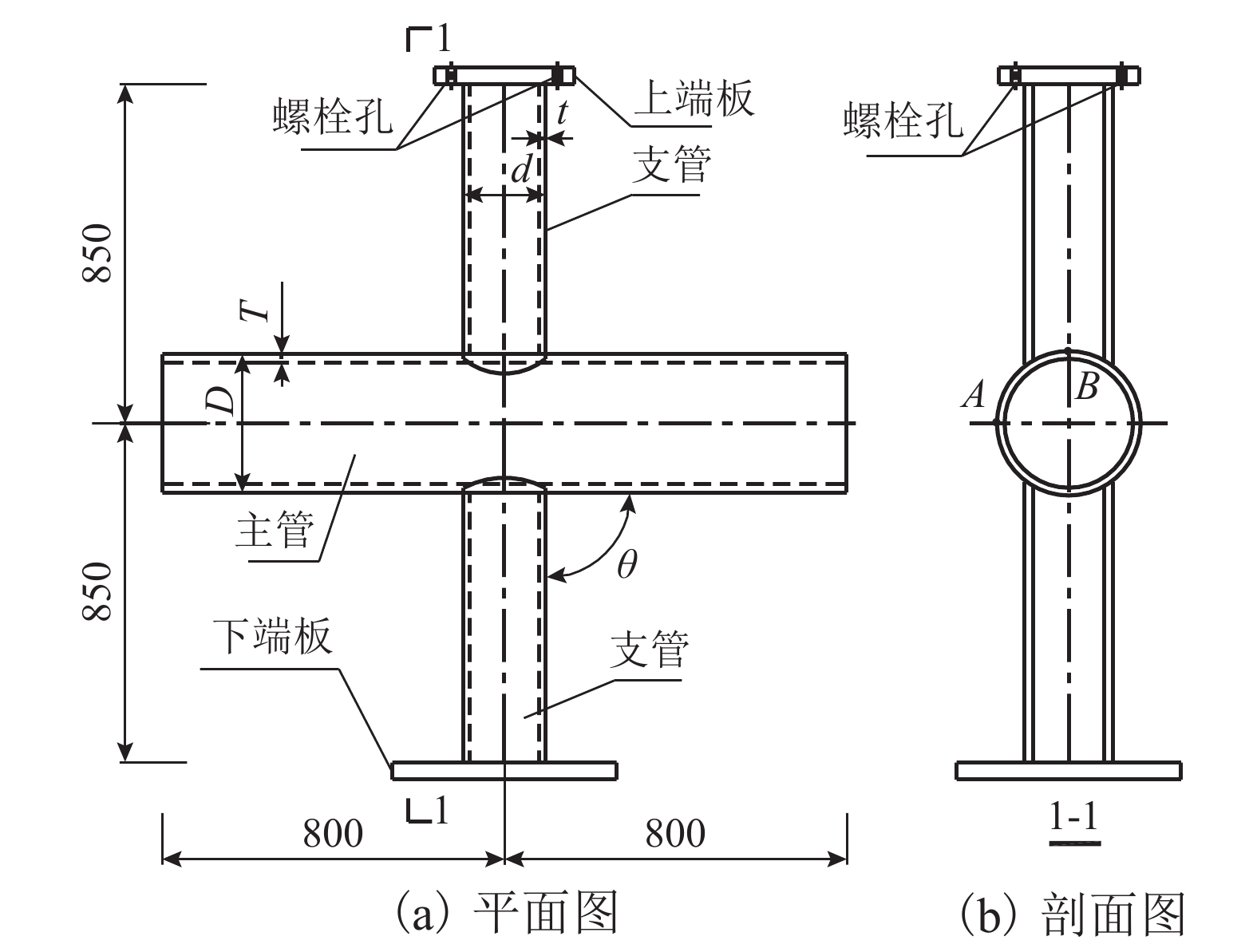
试件 D/mm d/mm T/mm t/mm β γ τ θ/(°) XPA 244.6 202.8 8.0 6.8 0.83 15.3 0.85 90 
下载: 导出CSV
表 2 钢管材性试验结果（平均值）
Table 2. Test results of steel tubing properties (average value)
钢管直径（壁厚）/mm fy/MPa fu/MPa E/GPa ζ/% 244.6（8.0） 375.3 545.1 209 32.7 202.8（6.8） 372.1 550.3 213 31.3
下载: 导出CSV
表 3 θ
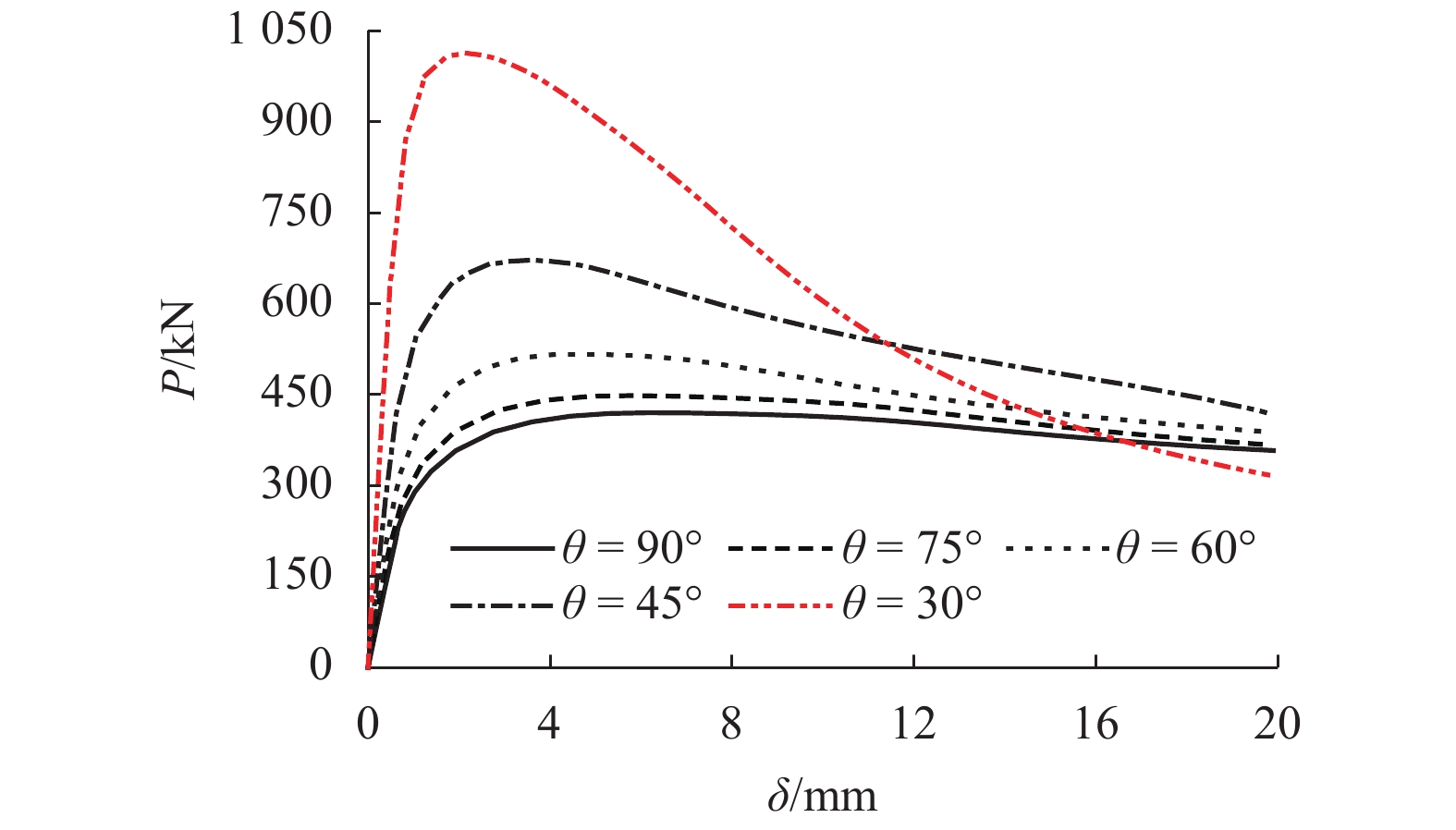
对节点受压承载力的影响 Table 3. Effect of θ on the Puc
项目 90° 75° 60° 45° 30° Puc/kN 419.9 441.3 516.4 671.3 1013.2 Pucsin θ/kN 419.9 426.3 447.2 474.7 506.6 Pucsin θ/Puc90 1.00 1.01 1.06 1.13 1.21
下载: 导出CSV
表 4 θ对ηt的影响
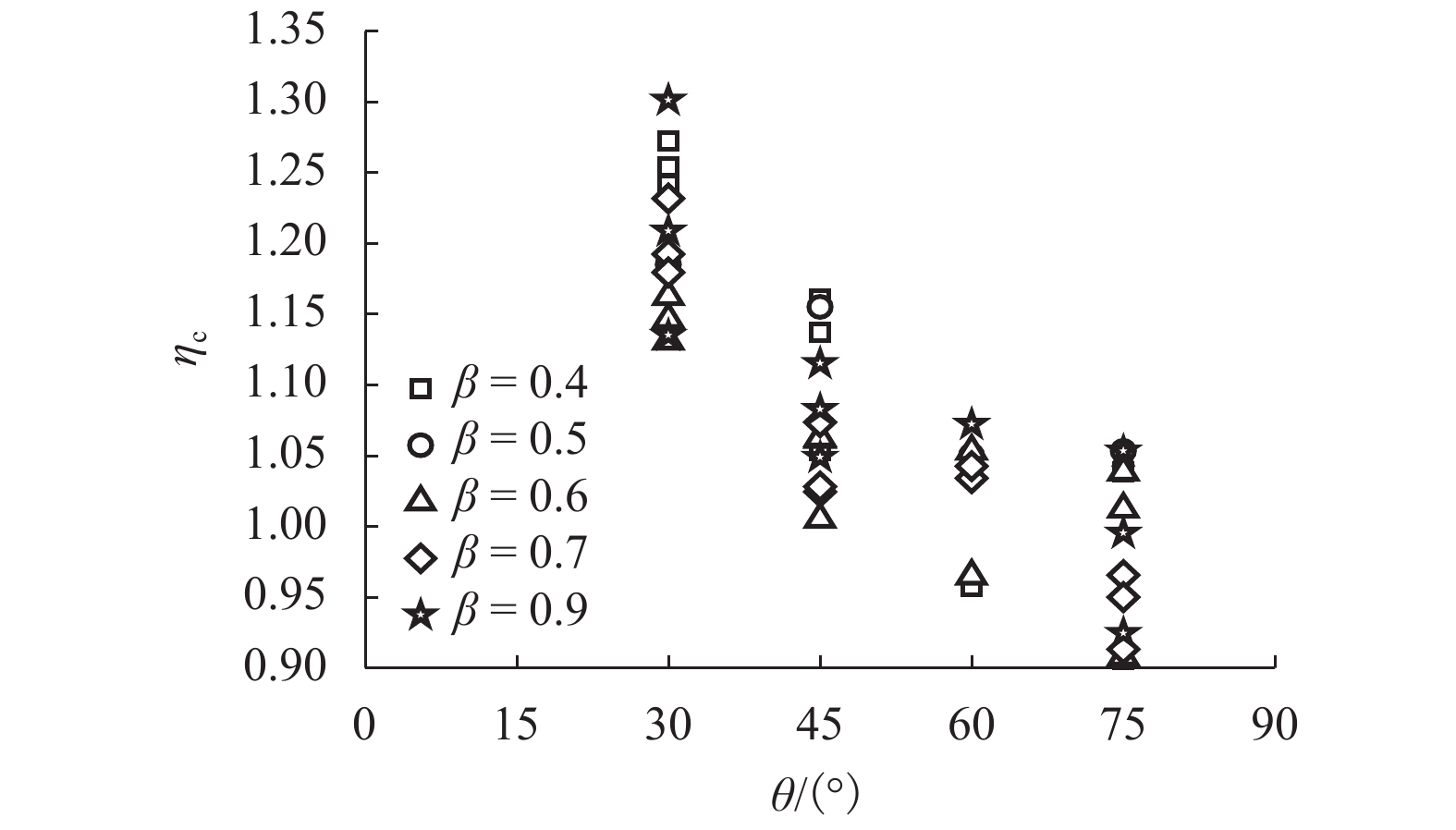
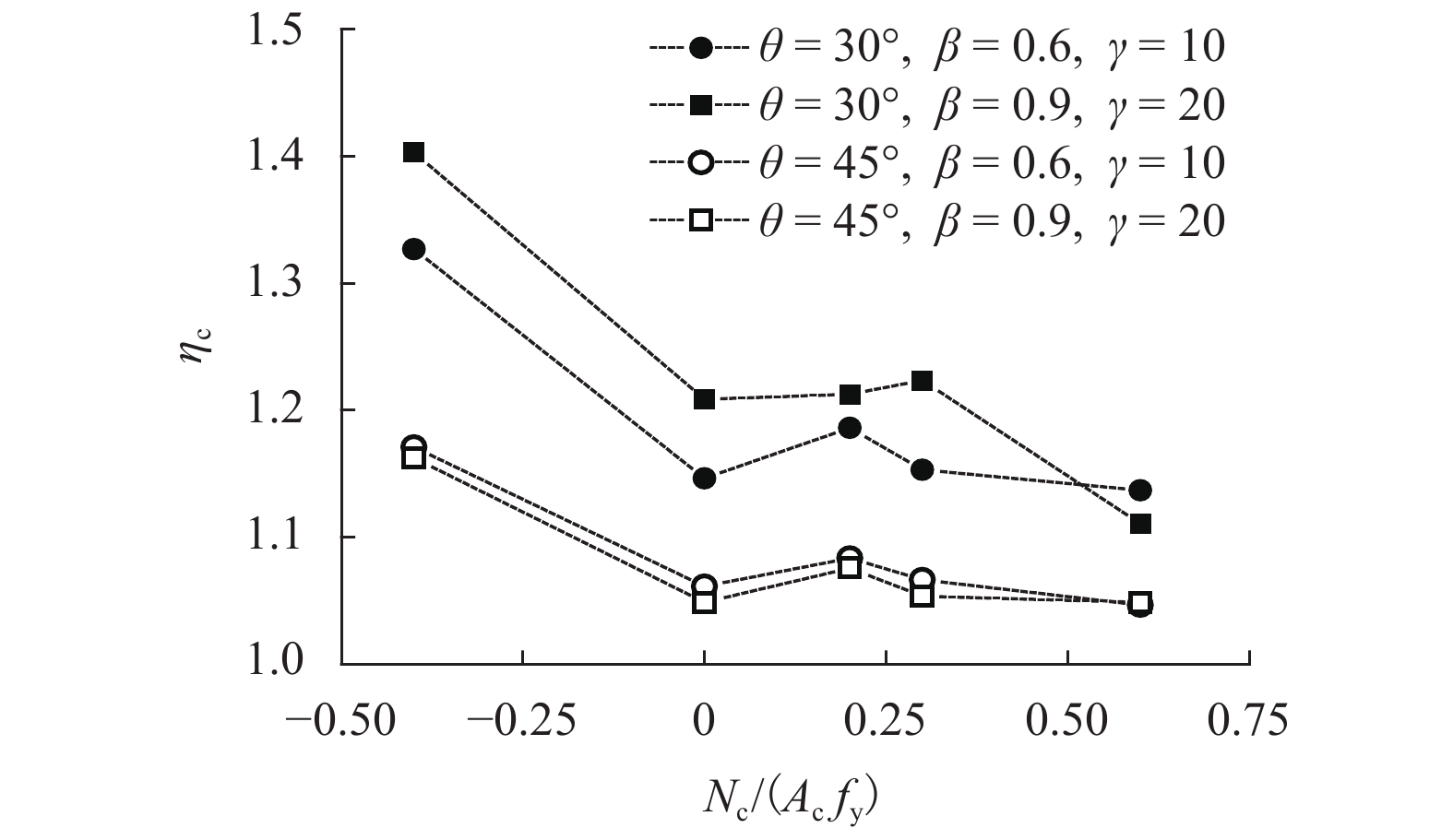
Table 4. Effect of θ on the ratio ηt
D/mm fy/MPa β γ θ/（°） Put/kN ηt 245 375 0.83 15.3 75 901.1 1.04 245 375 0.83 15.3 60 1016.4 1.05 245 375 0.83 15.3 45 1291.3 1.09 245 375 0.83 15.3 30 1860.5 1.12 250 345 0.90 10.0 75 2646.2 0.96 250 345 0.90 20.0 45 1491.1 0.98 250 345 0.90 40.0 30 932.2 1.11 250 345 0.70 10.0 45 1891.7 1.12 250 345 0.70 20.0 30 1062.8 1.34 250 345 0.70 40.0 75 107.6 1.03 250 345 0.40 10.0 30 1650.6 1.27 250 345 0.40 20.0 75 202.9 1.01 250 345 0.40 40.0 45 106.2 1.00
下载: 导出CSV
-
KUROBANE Y, MAKINO Y, OCHI K. Ultimate resistance of unstiffened tubular joints[J]. Journal of Structural Engineering, 1984, 110(2): 385-40. doi: 10.1061/(ASCE)0733-9445(1984)110:2(385) LU L H, WINKEL G D, YU Y, et al. Deformation limit for the ultimate strength of hollow section joints[C]// Sixth International Symposium on Tubular Structures. Melbourne: University of Melbourne, 1994: 341-347. PECKNOLD D, MARSHALL P, BUCKNELL J. New API RP2A tubular joint strength design provisions[J]. Journal of Energy Resources Technology, 2007, 129(3): 177-189. doi: 10.1115/1.2748811 王伟,陈以一,杜纯领,等. 上海光源工程屋盖钢管节点平面外受弯性能试验研究[J]. 建筑结构学报,2009,30(1): 75-81. doi: 10.3321/j.issn:1000-6869.2009.01.011WANG Wei, CHEN Yiyi, DU Chunling. et al. Experimental study on out-of-plane bending performance of tubular joints in steel roof for the Shanghai Synchrotron Radiation Facility[J]. Journal of Building Structures, 2009, 30(1): 75-81. doi: 10.3321/j.issn:1000-6869.2009.01.011 RAN Feng, BEN Young. Theoretical analysis of cold-formed stainless steel tubular joints[J]. Engineering Structures, 2015, 83(1): 99-115. 赵必大,刘成清,章圣冶,等. Y型圆钢管相贯节点的轴向刚度计算模型[J]. 西南交通大学学报,2015,50(5): 872-878. doi: 10.3969/j.issn.0258-2724.2015.05.016ZHAO Bida, LIU Chengqing, ZHANG Shenye, et al. Calculation model for axial rigidity of CHS Y-type joints[J]. Journal of southwest jiaotong university, 2015, 50(5): 872-878. doi: 10.3969/j.issn.0258-2724.2015.05.016 马昕煦,陈以一. 支方主圆T形相贯节点轴压承载力计算公式[J]. 工程力学,2017,34(5): 163-170.MA Xinxu, CHEN Yiyi. Ultimate strength formulae for RHS-CHS T-joints under axial compression[J]. Engineering Mechanics, 2017, 34(5): 163-170. 吴亮秦,李自林,韩庆华. 垫板加强N形圆钢管相贯节点静力性能试验研究[J]. 建筑结构学报,2010,31(10): 83-88.WU Liangqin, LI Zilin, HAN Qinghua. Experimental study on static behavior of plate reinforced tubular N- joints[J]. Journal of Building Structures, 2010, 31(10): 83-88. LEI Zhu, KAI Yang, YU Bai, et al. Capacity of steel CHS X-joints strengthened with external stiffening ring in compression[J]. Thin-Walled Structures, 2017, 115(6): 110-118. TOGO T, Experimental study on mechanical behavior of tubular joints[D]. Osaka: Osaka University, 1967. European Committee for Standardization. Eurocode3-design of steel structures-part 1.8: design of joints[S]. Brussels: CEN Press, 2005. 中冶建筑研究总院有限公司, 同济大学. 钢管结构技术规程: CECS280—2010[S]. 北京: 中国计划出版社, 2011. 中冶京诚工程技术有限公司. 钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2018. Health and Safety Executive. Offshore installations, guidance on design, construction and certification: L85 HSE[S]. Britain: HSE Press, 1998. International Standards Organization. Petroleum and natural gas industries-offshore structures: ISO 13819-2—1955[S]. London: BIS Press, 1996. 中冶建筑研究总院有限公司. 钢结构焊接规范: GB 50661—2011[S]. 北京: 中国建筑工业出版社, 2012. ANDREW P V, JEFFREY A P. Numerical study and design of skewed X-type branch plate-to-circular hollow section connections[J]. Journal of Constructional Steel Research, 2012, 68(1): 1-10. doi: 10.1016/j.jcsr.2011.06.005 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 632
- HTML全文浏览量: 320
- PDF下载量: 8
- 被引次数: 0