Damage Assessment Method for Concrete-Filled Steel Tubular Columns under Impact Loading
-
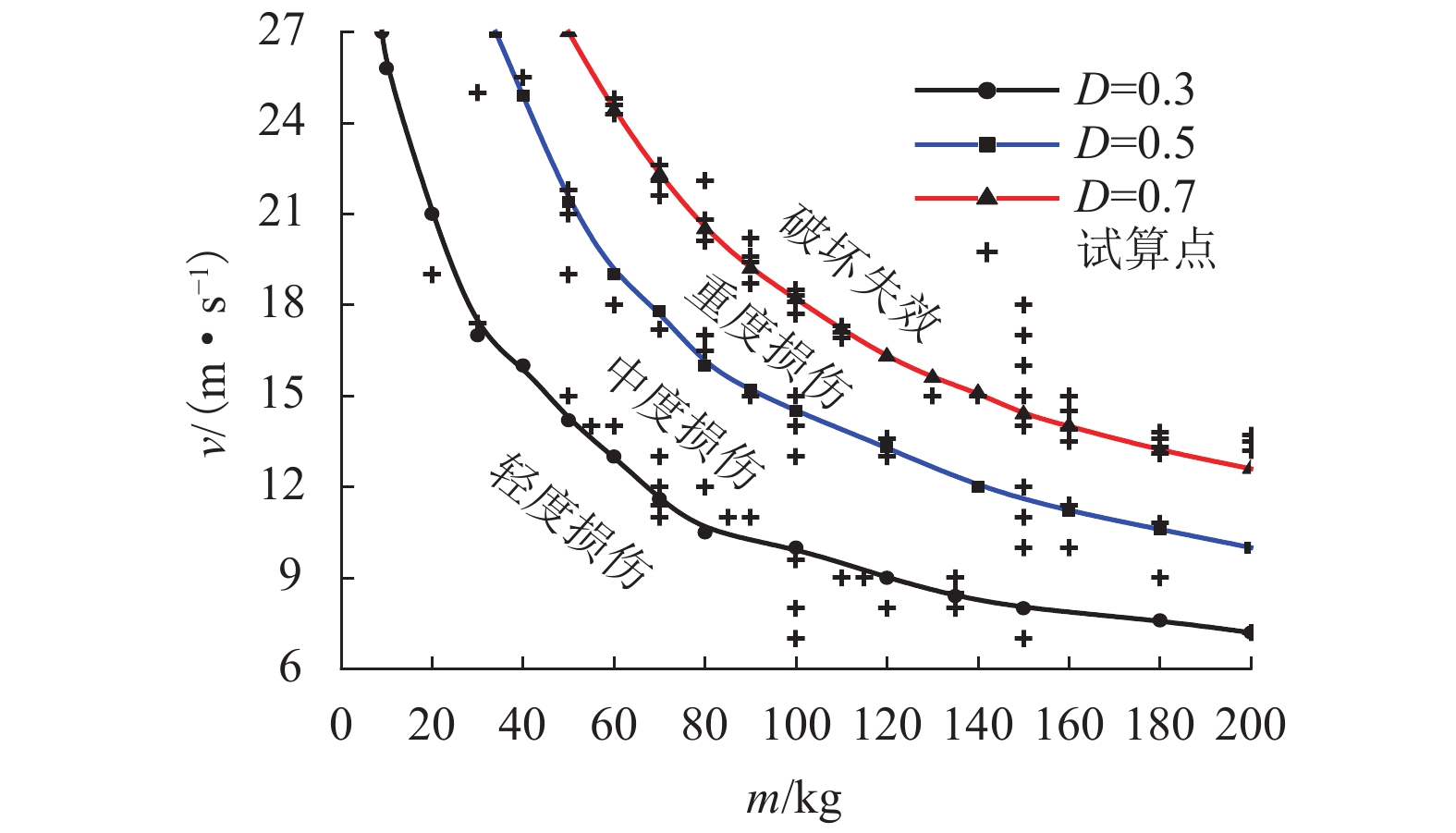
摘要: 为了建立侧向冲击荷载作用下钢管混凝土柱的损伤评估方法,以钢管混凝土柱近支座落锤冲击试验为基础,结合数值模拟和理论分析,研究预加轴力、冲击体质量及冲击速度对钢管混凝土柱损伤程度的影响. 选取冲击体质量和速度作为损伤评估主控变量,建立基于剩余承载力的损伤评估指标D的计算式,并划分损伤评估等级. 以典型钢管混凝土结构柱为例,通过仿真试算拟合其损伤评估曲线,并建立损伤评估的图解方法. 研究结果表明:冲击体质量和速度对钢管混凝土柱损伤程度的影响显著,预加轴力的影响呈现出变异性;D=0.3,0.5,0.7时的损伤评估曲线将坐标平面划分为4个面域,分别代表钢管混凝土柱发生轻度损伤、中度损伤、重度损伤及破坏失效;根据冲击体质量和速度的组合点与损伤评估曲线的位置关系,可以快速判定钢管混凝土柱的损伤程度.Abstract: In order to develop a damage assessment method for concrete-filled steel tubular (CFST) columns subjected to lateral impact, the drop hammer impact tests are carried out on CFST columns near supports. By the use of numerical simulation and theoretical analysis, the effects of pre-loading axial force, impact mass and impact velocity on the damage degree of CFST columns are studied. The impact mass and velocity are selected as the main control variables of damage assessment for CFST columns. Then the calculation formula D of damage assessment based on the residual bearing capacity is established and the levels of damage assessment are defined. The damage assessment method is given by taking a typical CFST column subjected to lateral impact. The damage assessment curves are fitted by simulation and trial calculation, and then the graphic method for damage assessment is established. The results show that the impact mass and velocity have great influence on the damage degree, while the effect of pre-loading axial force on the damage degree has great variability. The damage assessment curves (D=0.3, 0.5, 0.7) divide the coordinate plane into four regions, which respectively represent the slight damage, moderate damage, severe damage and failure for CFST columns. According to the position relationship between the combination point of the impact mass and velocity and the damage assessment curves, the damage degree of CFST columns can be quickly determined.
-
表 1 CFST试件冲击工况
Table 1. Impact conditions of CFST specimens
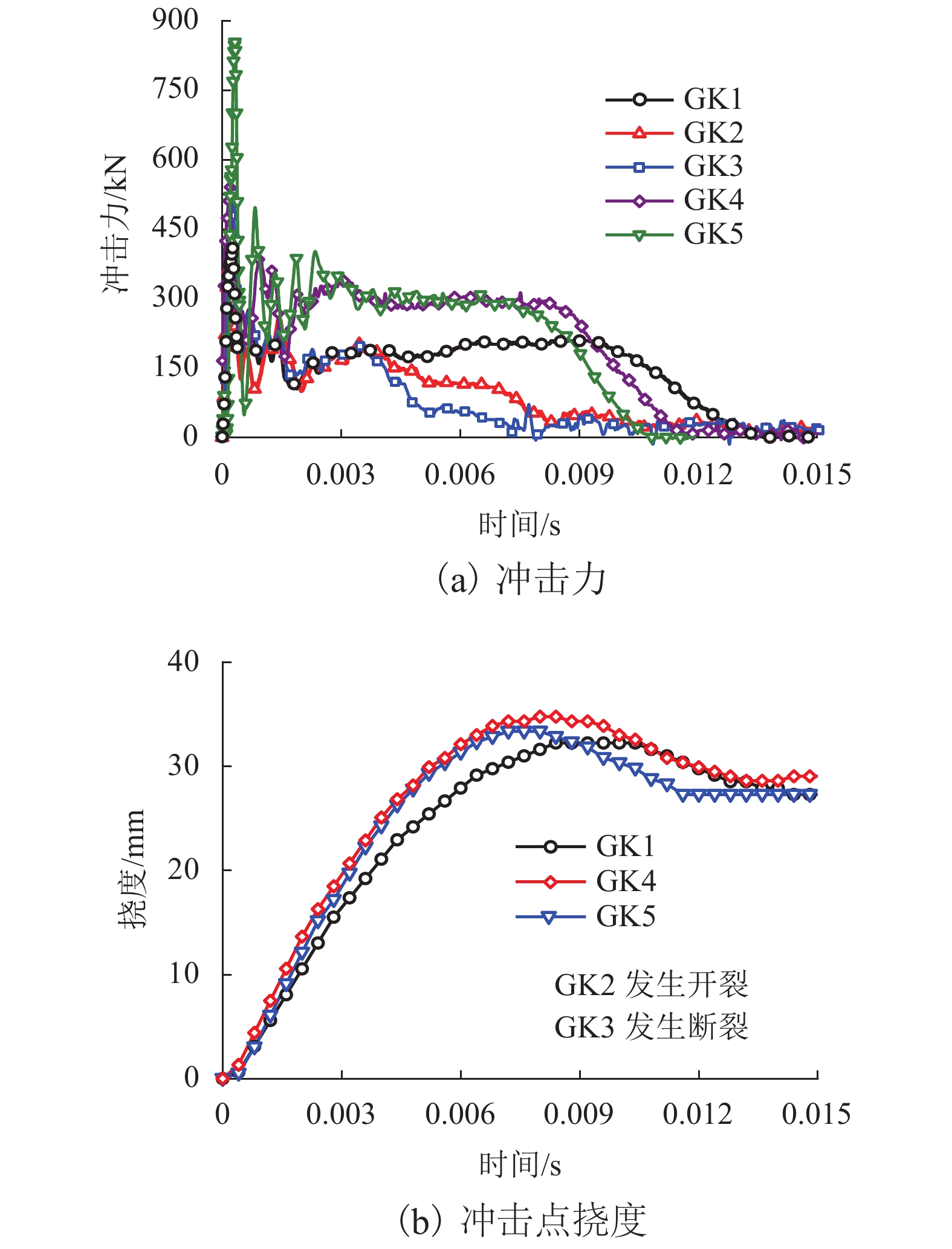
试件编号 钢管壁厚/mm 冲击高度/m 冲击速度/(m•s−1) 初始动能/J 预加轴力/kN GK1 2.0 3.0 7.67 7 938 0 GK2 2.0 5.0 9.90 13 230 0 GK3 2.0 7.0 11.71 18 522 0 GK4 3.5 5.0 9.90 13 230 0 GK5 3.5 5.0 9.90 13 230 200 表 2 不同参数下CFST构件的仿真结果
Table 2. Simulation results of CFST members with different parameters
工况 钢管壁
厚/mm冲击体
质量/kg冲击高
度/m预加轴
力/kN冲击力
峰值/kN最大挠度
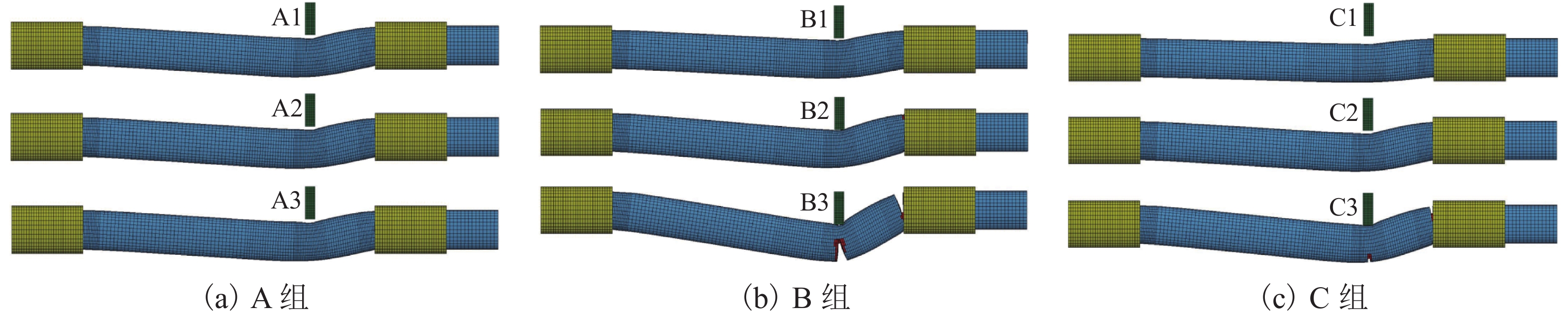
$\delta_{\max} $/mm支座转角/(°) 最大值 最小值 A1 3.5 270 6.0 0 545 38.5 11.0 3.0 A2 3.5 270 6.0 200 554 37.4 11.0 3.0 A3 3.5 270 6.0 500 557 37.3 11.0 3.0 B1 2.0 270 3.0 200 344 31.2 9.0 3.0 B2 2.0 270 5.0 200 427 51.1 14.0 4.0 B3 2.0 270 7.0 200 443 C1 2.0 100 5.0 200 414 18.2 5.0 1.0 C2 2.0 200 5.0 200 422 37.3 11.0 3.0 C3 2.0 300 5.0 200 427 55.4 15.0 5.0 注:L为冲击点到支座的距离,L = 200 mm 时,支座转角取最大值;L = 700 mm 时,支座转角取最小值. 表 3 CFST柱损伤评估等级
Table 3. Damage assessment levels of CFST columns
取值 (0,0.3] (0.3,0.5] (0.5,0.7] (0.7,1.0] 评估等级 轻度
损伤中度
损伤重度
损伤破坏
失效表 4 典型CFST柱设计参数
Table 4. Design parameters of the typical CFST column
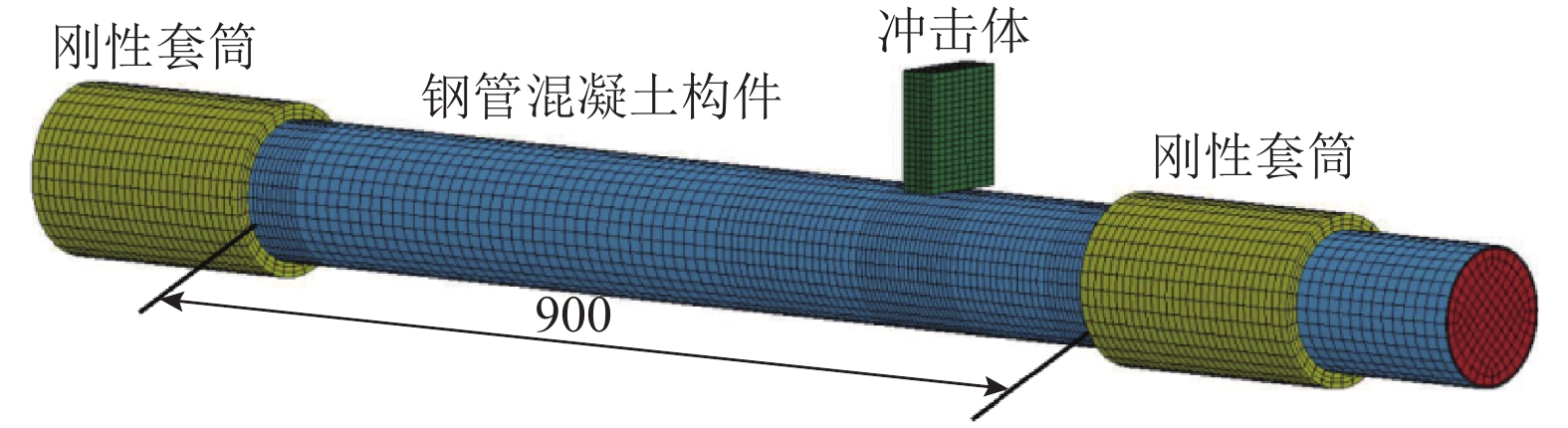
参数 有效长度/mm 钢管壁厚/mm 钢管外径/mm 预加轴力/kN 混凝土强度/MPa 钢材强度/MPa 长细比 取值 900 2.0 114 200 43.45 320 3.81 -
HAN Linhai, LI Wei, BJORHOVDE R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures:members[J]. Journal of Constructional Steel Research, 2014, 100: 211-228. doi: 10.1016/j.jcsr.2014.04.016 FENG Peng, CHENG Shi, BAI Yu, et al. Mechanical behavior of concrete-filled square steel tube with FRP-confined concrete core subjected to axial compression[J]. Composite Structures, 2015, 123: 312-324. 王新征, 李萍, 杨文喜, 等. 侧向冲击下钢管混凝土构件损伤演化数值分析[J]. 工程力学, 2013, 30(增刊1): 267-272.WANG Xinzheng, LI Ping, YANG Wenxi, et al. Damage evolution of concrete filled steel tube by lateral impact with numerical simulation[J]. Engineering Mechanics, 2013, 30(S1): 267-272. 赵武超,钱江,张文娜. 冲击荷载下钢筋混凝土梁的性能及损伤评估[J]. 爆炸与冲击,2019,39(1): 111-122.ZHAO Wuchao, QIAN Jiang, ZHANG Wenna. Performance and damage evaluation of RC beams under impact loading[J]. Explosion and Shock Waves, 2019, 39(1): 111-122. 刘飞,罗旗帜,蒋志刚. 低速冲击下RC梁的动态响应和破坏机理研究[J]. 工程力学,2015,32(5): 155-161.LIU Fei, LUO Qizhi, JIANG Zhigang. Dynamic responses and failure mechanism of RC beams to low velocity impact[J]. Engineering Mechanics, 2015, 32(5): 155-161. ZHAO Debo, YI Weijian, KUNNATH S K. Numerical simulation and shear resistance of reinforced concrete beams under impact[J]. Engineering Structures, 2018, 166: 387-401. doi: 10.1016/j.engstruct.2018.03.072 SHARMA H, HURLEBAUS S, GARDONI P. Performance-based response evaluation of reinforced concrete columns subject to vehicle impact[J]. International Journal of Impact Engineering, 2012, 43: 52-62. doi: 10.1016/j.ijimpeng.2011.11.007 SHARMA H, GARDONI P, HURLEBAUS S. Probabilistic demand model and performance-based fragility estimates for RC column subject to vehicle collision[J]. Engineering Structures, 2014, 74: 86-95. doi: 10.1016/j.engstruct.2014.05.017 SHARMA H, GARDONI P, HURLEBAUS S. Performance-based probabilistic capacity models and fragility estimates for RC columns subject to vehicle collision[J]. Computer-Aided Civil and Infrastructure Engineering, 2015, 30(7): 555-569. doi: 10.1111/mice.12135 AGRAWAL A K, LIU G Y, ALAMPALLI S. Effects of truck impacts on bridge piers[C]//Advanced Materials Research. Switzerland: Trans Tech Publications, 2013: 13-25. 田力,朱聪. 碰撞冲击荷载作用下钢筋混凝土柱的损伤评估及防护技术[J]. 工程力学,2013,30(9): 144-150.TIAN Li, ZHU Cong. Damage evaluation and protection technique of RC columns under impulsive load[J]. Engineering Mechanics, 2013, 30(9): 144-150. LI Qingming, MENG Hui. Pulse loading shape effects on pressure-impulse diagram of an elastic-plastic,single-degree-of-freedom structural model[J]. Inter- national Journal of Mechanical Sciences, 2002, 44(9): 1985-1998. doi: 10.1016/S0020-7403(02)00046-2 FALLAH A S, LOUCA L A. Pressure-impulse diagrams for elastic-plastic-hardening and softening single-degree-of-freedom models subjected to blast loading[J]. International Journal of Impact Engineering, 2007, 34(4): 823-842. doi: 10.1016/j.ijimpeng.2006.01.007 SHI Yanchao, HAO Hong, LI Zhongxian. Numerical derivation of pressure-impulse diagrams for prediction of RC column damage to blast loads[J]. International Journal of Impact Engineering, 2008, 35(11): 1213-1227. doi: 10.1016/j.ijimpeng.2007.09.001 田志敏,章峻豪,江世永. 钢板混凝土复合梁在爆炸荷载作用下的损伤评估研究[J]. 振动与冲击,2016,35(4): 42-48.TIAN Zhimin, ZHANG Junhao, JIANG Shiyong. Damage assessment for steel-concrete composite beams subjected to blast loading[J]. Journal of Vibration and Shock, 2016, 35(4): 42-48. 闫秋实,杜修力. 典型地铁车站柱在爆炸荷载作用下损伤评估方法研究[J]. 振动与冲击,2017,36(1): 1-7.YAN Qiushi, DU Xiuli. Damage evaluation for a column of a typical subway station subjectedto internal blast loading[J]. Journal of Vibration and Shock, 2017, 36(1): 1-7. 中华人民共和国住房和城乡建设部.钢管混凝土结构技术规范: GB 50936—2014[S]. 北京: 中国建筑工业出版社, 2014. Comite Euro-International du Beton. CEB-FIP model code 1990[M]. Trowbridge: Redwood Books; 1993: 48-51. COWPER G R, SYMONDS P S. Strain-hardening and strain-rate effects in the impact loading of cantilever beams[R]. Providence: Brown University, 1957. 宋家欢. 钢管混凝土柱冲击动力响应的等效单自由度方法研究[D]. 成都: 西南交通大学, 2017. 师燕超. 爆炸荷载作用下钢筋混凝土结构的动态响应行为与损伤破坏机理[D]. 天津: 天津大学, 2009. 钟善桐. 钢管混凝土结构[M]. 北京: 清华大学出版社, 2003: 141-142. -





 下载:
下载: