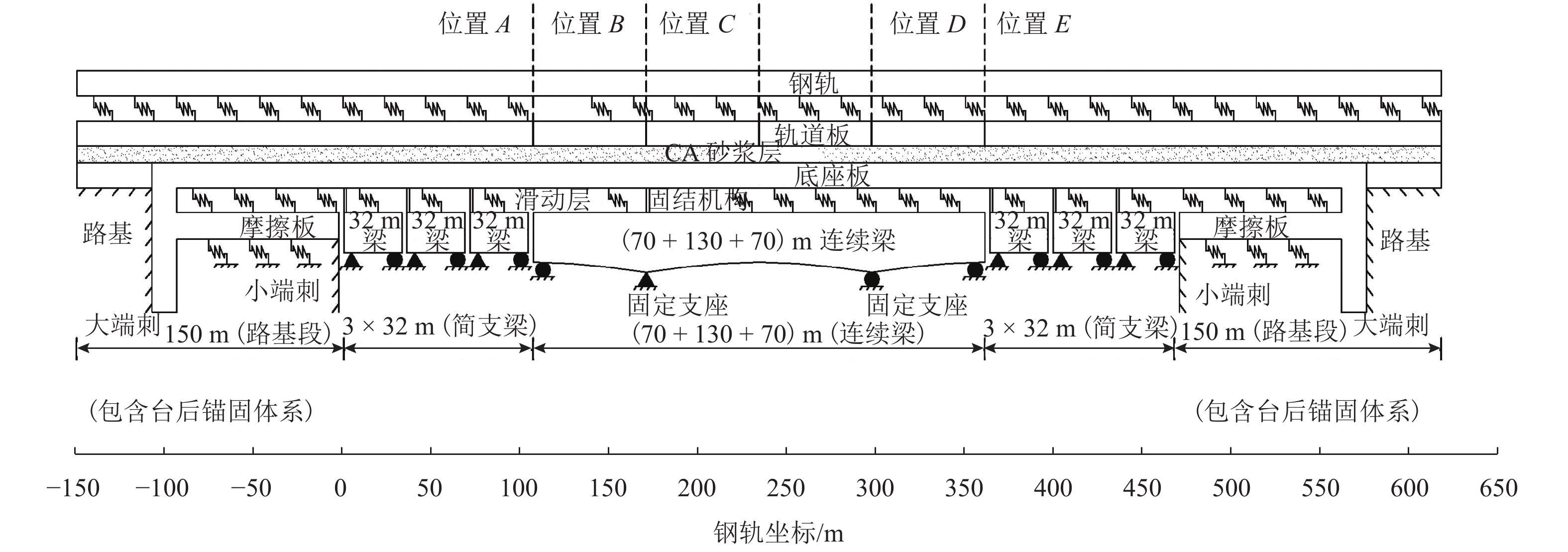
Expansion-Constriction Force Characteristics of Continuously Rails on Bridge under Fracture Condition of CRTS Ⅱ Track Slab Welded
-
摘要: 为了研究桥上CRTSⅡ型轨道板断裂条件下轨道、桥梁结构纵向受力变形规律及其影响，基于有限元法和梁-板-轨相互作用机理，建立桥上CRTSⅡ型板式无砟轨道无缝线路空间耦合模型，分析不同轨道板断缝位置、断缝宽度、裂缝深度及轨道板、底座板伸缩刚度对断板条件下桥上无砟轨道无缝线路伸缩力分布规律的影响. 研究结果表明：在计算轨道板断裂条件下桥上无砟轨道无缝线路伸缩力时，应根据不同检算部件选取最不利的断板位置，建议将轨道板断缝宽度和深度分别取2 mm和200 mm、轨道板、底座板伸缩刚度折减至10%～50%，计算结果是偏安全的且不失一般性；轨道板断裂增加了断缝处CA （cement asphalt）砂浆层及底座板断裂的风险，断板侧的钢轨纵向位移及轨板相对位移均在断缝处急剧变化.Abstract: In order to study the longitudinal stress and deformation characteristics and their influences on track and bridge structure under the fracture condition of CRTSⅡ track slab, a spatial coupling model based on the finite element method and bridge-slab-rail interaction mechanism was established. This model can analyze the influences of crack location, width and depth of track slabs, as well as the expansion-constriction stiffness of track slab and bed plate, on distribution rules of the expansion-constriction force of continuously welded rail (CWR) on bridge. Results show that, in order to calculate the expansion-constriction force of CWR on bridge under the fracture condition of CRTSⅡ track slab, a most unfavorable fracture location at track slab should be selected according to the different checking parts. Meanwhile, the crack width and depth of track slab are suggested to be 2 mm and 200 mm, respectively, and the expansion-constriction stiffness of track slab and bed plate should be reduced to 10%−50%, since in this way the calculation result is conservative without losing generality. Track slab fracture increases the fracture risk of cement asphalt mortar screed and bed plate; the longitudinal displacement of rail and the relative displacement between rail and track slab on the side of broken slab are changed dramatically at the crack.
-
Key words:
- CRTSⅡ slab track /
- CWR on bridge /
- track slab fracture /
- crack location /
- crack width /
- crack depth
-
图 4 不同轨道板断缝位置工况下钢轨纵向力
Figure 4. Longitudinal forces of rail under different crack locations of track slab
图 5 不同轨道板断缝宽度条件下钢轨纵向力
Figure 5. Longitudinal forces of rail under different crack widths of track slab
图 6 不同轨道板裂缝深度条件下钢轨纵向力
Figure 6. Longitudinal forces of rail under different crack depths of track slab
图 7 不同轨道板裂缝深度条件下轨道板内部纵向应力
Figure 7. Longitudinal stresses in track slab under different crack depths of track slab
图 8 不同轨道板裂缝深度条件下轨道板内部裂缝宽度
Figure 8. Crack widths in track slab under different crack depths of track slab
图 9 不同轨道板、底座板伸缩刚度条件下钢轨纵向力
Figure 9. Longitudinal forces of rail under different expansion-constriction stiffness of track slab and bed plate
表 1 主要结构物理量符号
Table 1. Symbolic representation of main structural physical quantities
结构名称 物理量 符号 钢轨 纵向力 Fr 纵向位移 Dr 轨道板 上表面纵向应力 Stsu 下表面纵向应力 Stsl 上表面纵向位移 Dtsu CA砂浆层 纵向应力 SCAm 底座板 上表面纵向应力 Sbpu 下表面纵向应力 Sbpl 下表面纵向位移 Dbpl 桥梁梁体 纵向位移 Db 桥台 纵向力 Fa 纵向位移 Da 桥墩 纵向力 Fp 纵向位移 Dp 钢轨轨道板 相对位移 ∆Drts 轨道板底座板 相对位移 ∆Dtsbp 底座板桥梁 相对位移 ∆Dbpb 
下载: 导出CSV
表 2 主要结构纵向力最大值
Table 2. Maximum longitudinal forces of main structures
轨道板断裂工况 Fr/kN Stsu/MPa Stsl/MPa SCAm/MPa Sbpu/MPa Sbpl/MPa Fa/kN Fp/kN 压（应）力 拉（应）力 未断板 −46.865 10.835 21.901 16.093 2.783 12.735 16.416 341.731 183.594 断板（断板侧） −47.731 30.343 16.310 155.824 16.287 43.736 21.161 339.867 176.715 断板（非断板侧） −46.902 12.537 21.211 15.747 2.741 12.390 15.403
下载: 导出CSV
表 3 主要结构位移最大值
Table 3. Maximum longitudinal displacements of main structures
mm 轨道板断裂工况 Dr ∆Drts Dtsu ∆Dtsbp Dbpl ∆Dbpb Db Da Dp 压缩变形 拉伸变形 未断板 −1.727 1.041 0.192 −1.755 0.015 −1.745 56.927 −58.392 1.139 1.476 断板（断板侧） −1.854 1.009 0.368 −2.111 0.083 −1.876 56.837 −58.458 1.133 1.457 断板（非断板侧） −1.768 1.009 0.192 −1.796 0.016 −1.787 56.948 −58.447
下载: 导出CSV
表 4 不同轨道板断缝位置条件下伸缩力计算结果
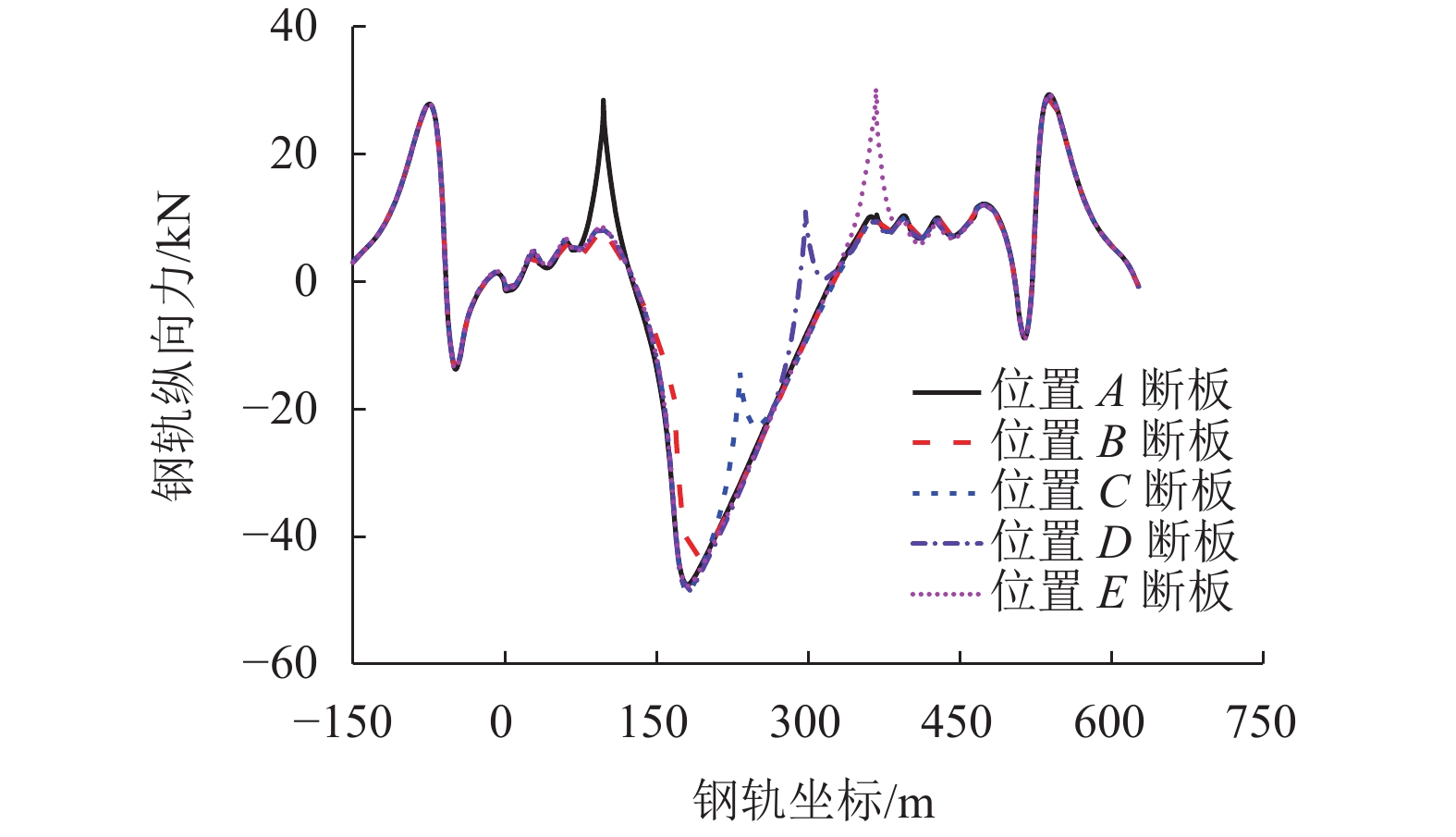
Table 4. Calculation results of expansion-constriction force with different crack locations of track slab
轨道板断缝位置 Fr/kN Dr/mm ∆Drts/mm Stsu/MPa Stsl/MPa SCAm/MPa Sbpu/MPa Sbpl/MPa 压（应）力 拉（应）力 压缩变形 拉伸变形 位置 A −47.583 28.430 −1.695 1.164 0.345 21.978 151.994 15.506 42.121 19.708 位置 B −43.014 10.496 −1.668 0.965 0.412 21.970 129.348 13.173 35.830 17.602 位置 C −48.545 10.502 −1.66 1.011 0.303 21.968 136.862 13.888 38.001 17.499 位置 D −48.600 11.390 −1.719 1.007 0.336 21.967 149.018 15.294 41.214 19.205 位置 E −47.731 30.343 −1.854 1.009 0.368 16.310 155.824 16.287 43.736 24.161
下载: 导出CSV
表 5 不同轨道板断缝宽度条件下伸缩力计算结果
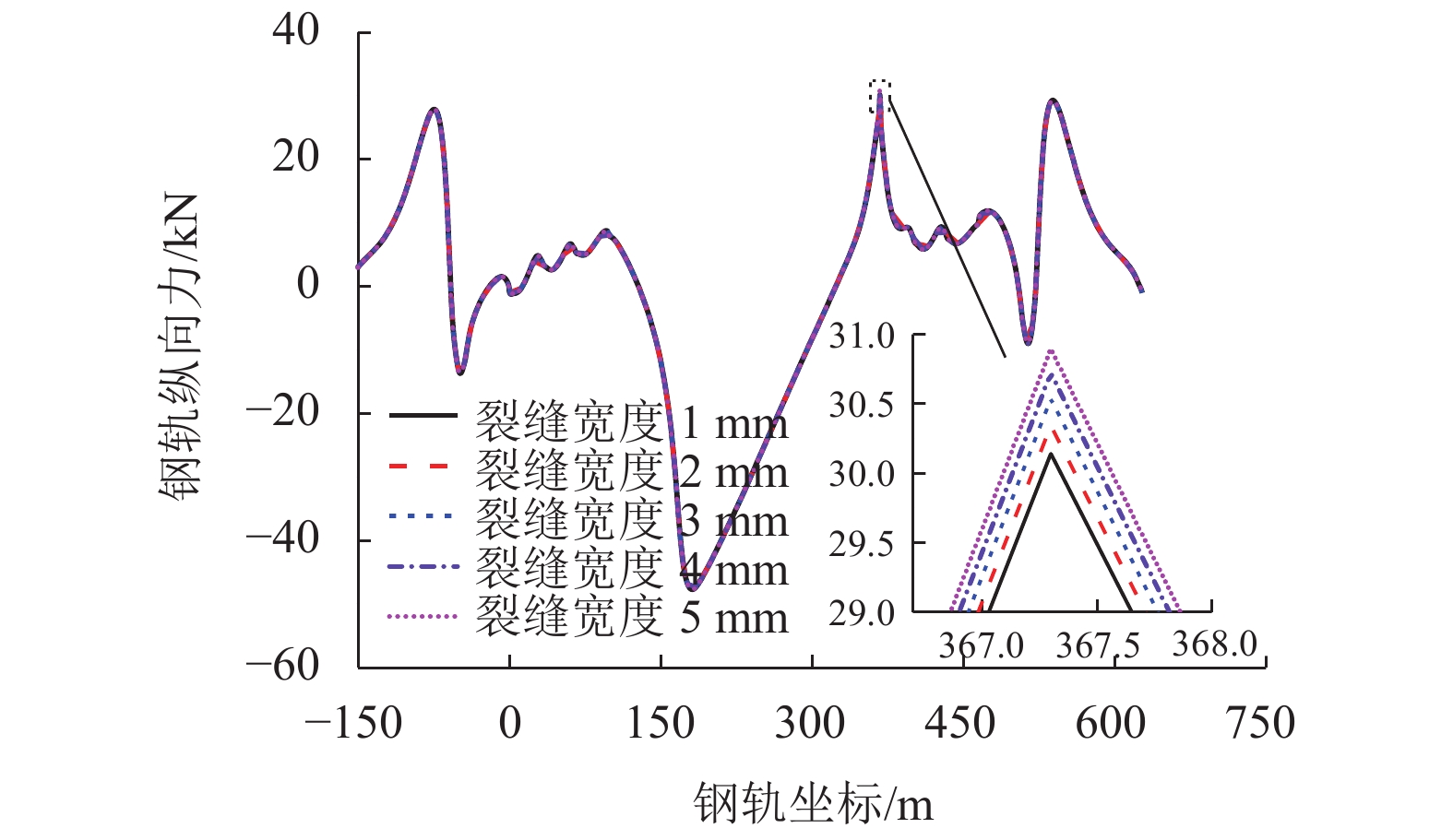
Table 5. Calculation results of expansion-constriction forces with different crack widths of track slab
轨道板断缝
宽度/mmFr/kN Dr/mm ∆Drts/mm Stsu/MPa Stsl/MPa SCAm/MPa Sbpu/MPa Sbpl/MPa 压（应）力 拉（应）力 压缩变形 拉伸变形 1 −47.721 30.141 −1.853 1.009 0.366 16.310 160.817 16.594 43.058 24.089 2 −47.731 30.343 −1.854 1.009 0.368 16.310 155.824 16.287 43.736 24.161 3 −47.741 30.536 −1.856 1.008 0.371 16.310 151.089 16.033 44.371 24.230 4 −47.750 30.720 −1.857 1.008 0.373 16.309 146.597 15.819 44.966 24.296 5 −47.759 30.895 −1.858 1.008 0.376 16.309 142.325 15.634 45.524 24.358
下载: 导出CSV
表 6 不同轨道板裂缝深度条件下纵向力和位移最大值计算结果
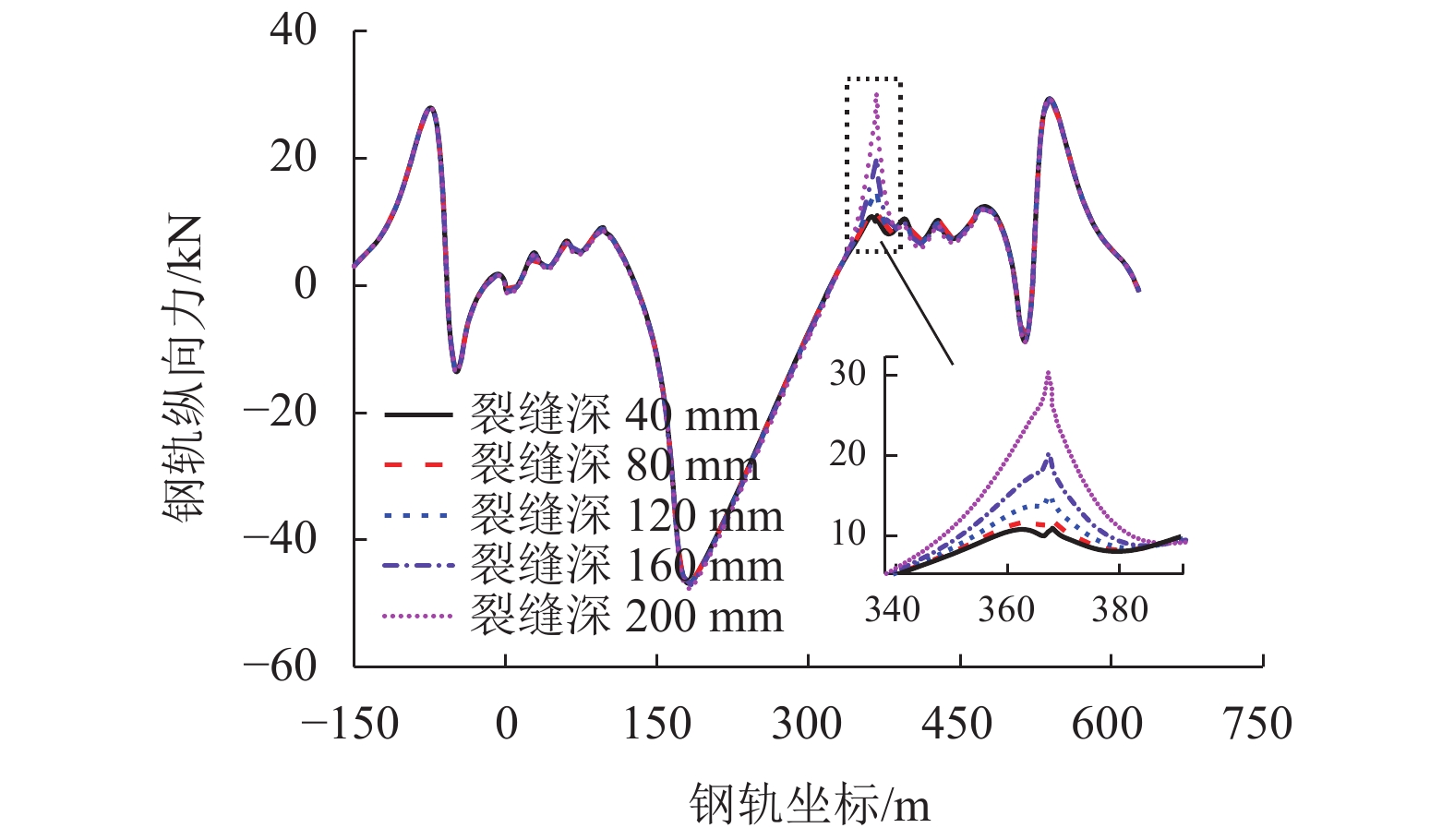
Table 6. Calculation results of maximum longitudinal forces and maximum longitudinal displacements with different crack depths of track slab
轨道板裂缝
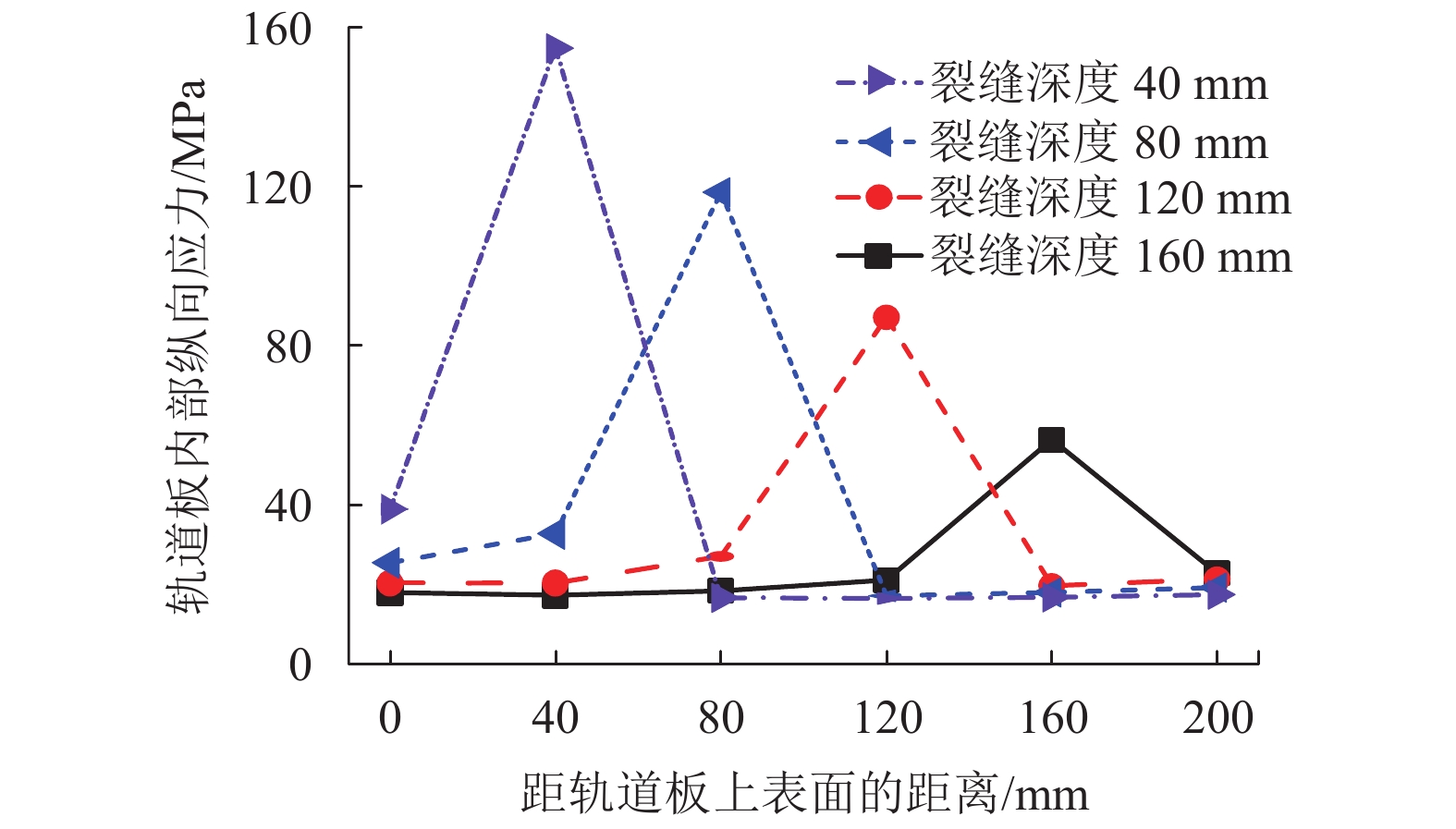
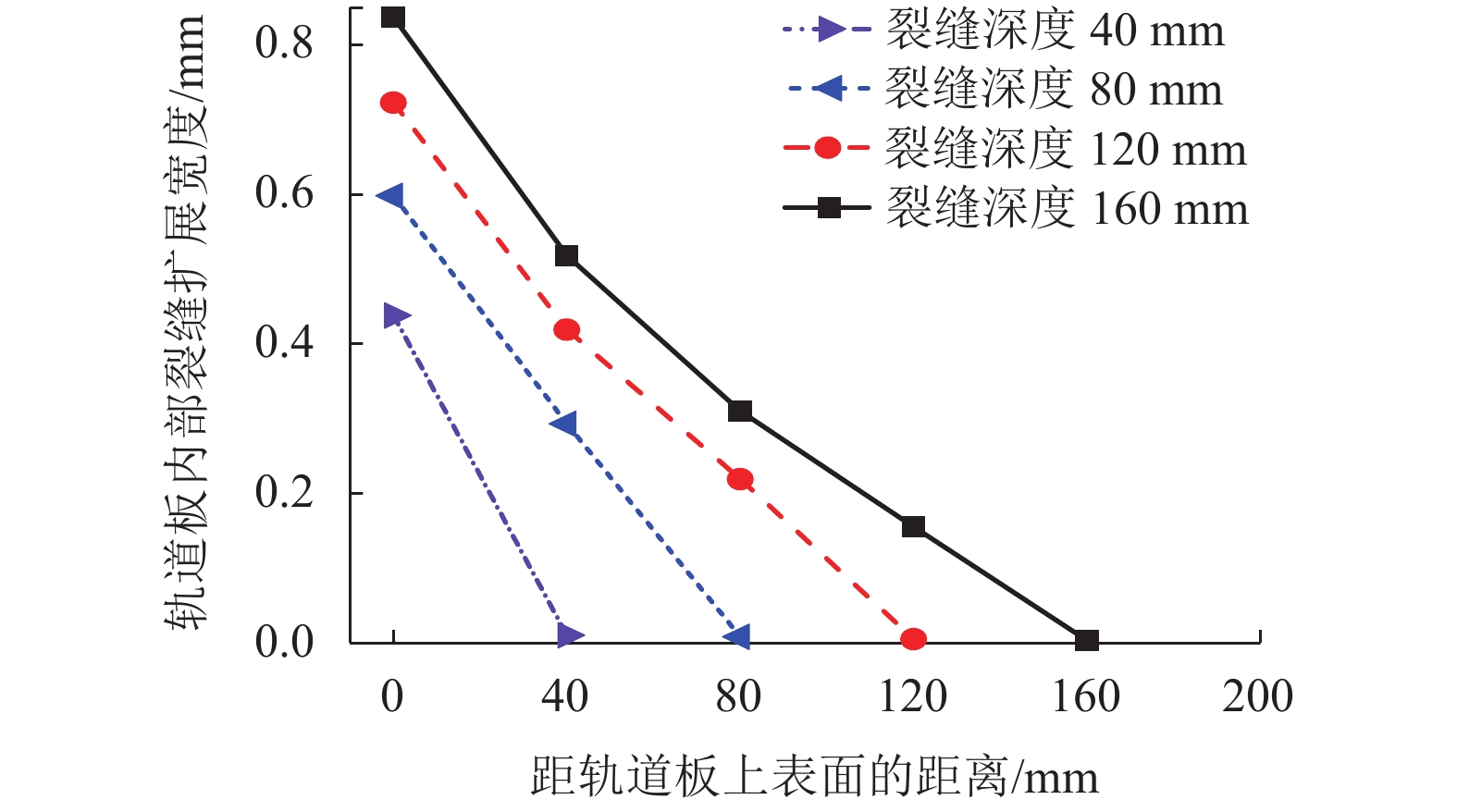
深度/mmFr/kN Dr/mm ∆Drts/mm Stsu/MPa Stsl/MPa SCAm/MPa Sbpu/MPa Sbpl/MPa 压（应）力 拉（应）力 压缩变形 拉伸变形 0 −46.865 10.835 −1.727 1.041 0.192 21.901 16.093 2.783 12.735 16.416 40 −46.875 10.973 −1.729 1.040 0.192 21.313 16.819 2.825 13.049 16.610 80 −46.922 12.060 −1.736 1.038 0.193 19.965 19.036 3.527 14.149 17.262 120 −47.033 14.965 −1.753 1.033 0.193 18.006 23.813 4.950 17.193 18.498 160 −47.256 20.258 −1.786 1.025 0.226 16.313 36.464 7.741 24.019 20.548 200 −47.731 30.343 −1.854 1.009 0.368 16.310 155.824 16.287 43.736 24.161
下载: 导出CSV
表 7 不同轨道板/底座板伸缩刚度条件下纵向力和位移最大值计算结果
Table 7. Calculation results of maximum longitudinal forces and maximum longitudinal displacements under different expansion-constriction stiffness of track slab and bed
轨道板、底座板
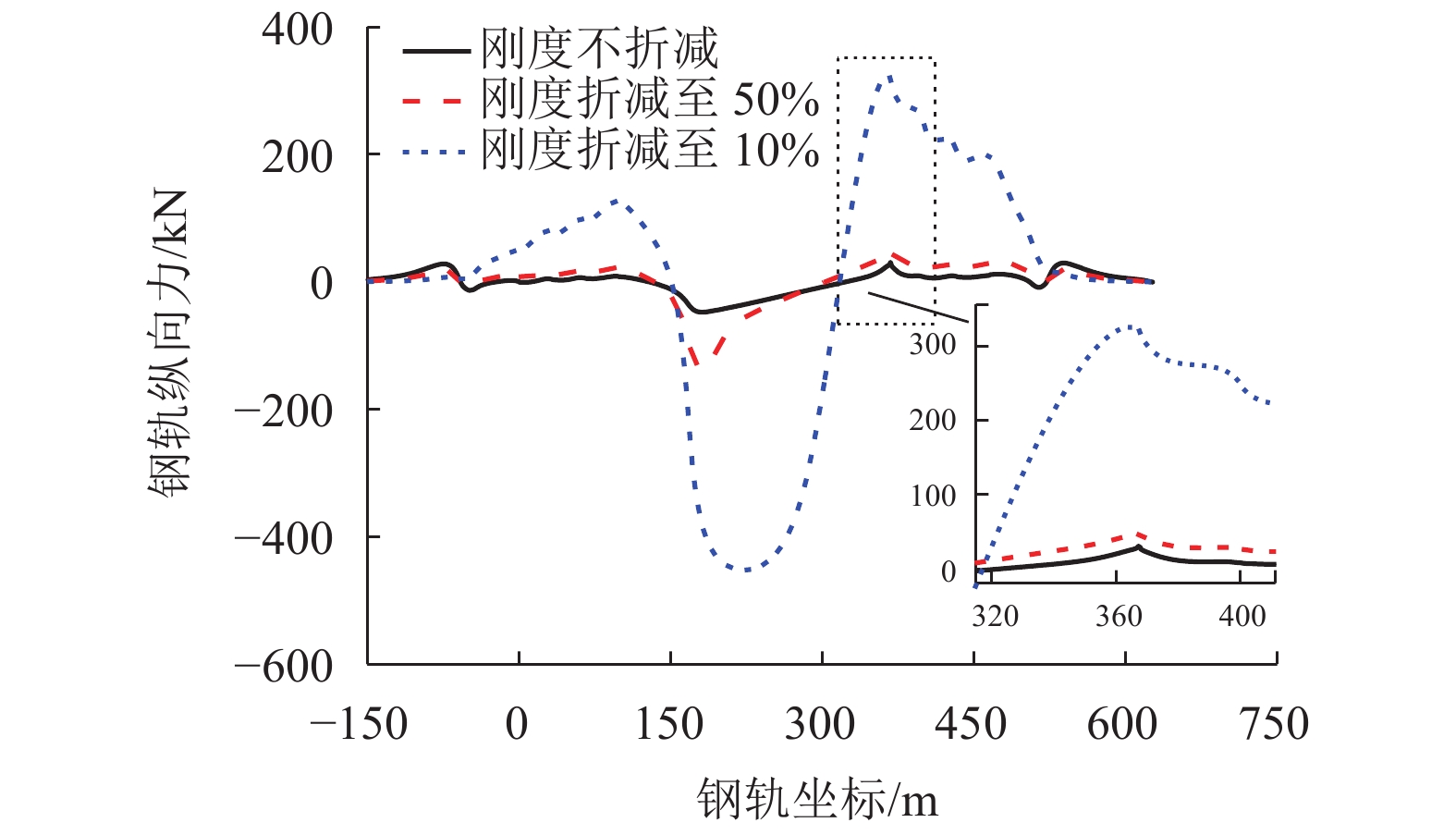
伸缩刚度Dr/mm Stsu/MPa Stsl/MPa SCAm/MPa Sbpu/MPa Sbpl/MPa Fa/kN Fp/kN 压缩变形 拉伸变形 刚度不折减 −1.854 1.009 16.310 155.824 16.287 43.736 21.161 339.867 176.715 刚度折减至30% −3.668 1.705 8.632 77.718 8.126 22.166 13.908 315.230 364.641 刚度折减至10% −24.435 9.100 2.527 21.475 2.242 6.438 4.838 455.361 2 062.186
下载: 导出CSV
-
谢铠泽,王平,徐井芒,等. 桥上单元板式无砟轨道无缝线路的适应性[J]. 西南交通大学学报,2014,49(4): 649-655. doi: 10.3969/j.issn.0258-2724.2014.04.014XIE Kaize, WANG Ping, XU Jingmang, et al. Adaptability of continuous welded rail of unit slab non-ballast track on bridges[J]. Journal of Southwest Jiaotong University, 2014, 49(4): 649-655. doi: 10.3969/j.issn.0258-2724.2014.04.014 王继军,江成,赵磊,等. 高铁单元板式无砟轨道大跨梁端适应性对比[J]. 铁道工程学报,2018,35(5): 18-23,87. doi: 10.3969/j.issn.1006-2106.2018.05.004WANG Jijun, JIANG Cheng, ZHAO Lei, et al. The adaptive contrast research on the slab track of high-speed railway in long span bridge end[J]. Journal of Railway Engineering Society, 2018, 35(5): 18-23,87. doi: 10.3969/j.issn.1006-2106.2018.05.004 YAN Bin, DAI Gonglian, ZHANG Huaping. Beam-track interaction of high-speed railway bridge with ballast track[J]. Journal of Central South University, 2012, 19(5): 1447-1453. doi: 10.1007/s11771-012-1161-8 MIN K H, YUN K M. An experimental study for longitudinal resistance of ballast track on bridge[J]. Journal of the Korea Academia-Industrial cooperation Society, 2016, 17(5): 173-178. doi: 10.5762/KAIS.2016.17.5.173 PAPP H, LIEGNER N. Investigation of internal forces in the rail due to the interaction of CWR tracks and steel railway bridges with ballasted track superstructure[J]. Pollack Periodica, 2016, 11(2): 65-74. doi: 10.1556/606.2016.11.2.6 LEE K C, JANG S Y, JUNG D K, et al. Evaluation of stress reduction of continuous welded rail of sliding slab track from track-bridge interaction analysis[J]. Journal of the Korean Society of Civil Engineers, 2015, 35(5): 1179-1189. doi: 10.12652/Ksce.2015.35.5.1179 张鹏飞. 复杂荷载条件下桥上CRTS Ⅱ型板式无砟轨道无缝线路纵向力研究[D]. 北京: 北京交通大学, 2018. 徐庆元,张旭久. 高速铁路博格纵连板桥上无砟轨道纵向力学特性[J]. 中南大学学报(自然科学版),2009,40(2): 526-532.XU Qingyuan, ZHANG Xujiu. Longitudinal forces characteristic of bogl longitudinal connected ballastless track on high-speed railway bridge[J]. Journal of Central South University (Science and Technology), 2009, 40(2): 526-532. 刘亚男. 复杂温度下Ⅱ型板式无砟轨道宽窄接缝病害影响及维修措施[D]. 北京: 北京交通大学, 2016. 赵林,刘学毅,赵华卫,等. CRTSⅡ型板式轨道宽接缝开裂对轨道受力的影响分析[J]. 铁道科学与工程学报,2016,13(1): 9-14. doi: 10.3969/j.issn.1672-7029.2016.01.002ZHAO Lin, LIU Xueyi, ZHAO Huawei, et al. The study of influence on track stress caused by the cracking at wide juncture of CRTSⅡ prefabricated slab track[J]. Journal of Railway Science and Engineering, 2016, 13(1): 9-14. doi: 10.3969/j.issn.1672-7029.2016.01.002 徐浩,谢铠泽,陈嵘,等. CRTSⅡ型板式轨道宽接缝开裂及修补材料对轨道板的影响分析[J]. 铁道标准设计,2012(7): 30-32,37. doi: 10.3969/j.issn.1004-2954.2012.07.008XU Hao, XIE Kaize, CHEN Rong, et al. Influence on track slab caused by crack and repairing material at wide juncture of CRTSⅡ slab-type track[J]. Railway Standard Design, 2012(7): 30-32,37. doi: 10.3969/j.issn.1004-2954.2012.07.008 徐庆元,张泽,陈效平,等. 桥上CRTSⅡ型板式无砟轨道混凝土疲劳寿命预测模型试验研究[J]. 铁道科学与工程学报,2017,14(8): 1565-1570. doi: 10.3969/j.issn.1672-7029.2017.08.001XU Qingyuan, ZHANG Ze, CHEN Xiaoping, et al. Experimental study on fatigue life prediction model of concrete of CRTSⅡ slab track on bridge[J]. Journal of Railway Science and Engineering, 2017, 14(8): 1565-1570. doi: 10.3969/j.issn.1672-7029.2017.08.001 徐庆元,林青腾,方子匀,等. 桥上纵连板式无砟轨道疲劳应力谱的理论研究[J]. 西南交通大学学报,2018,53(5): 906-912. doi: 10.3969/j.issn.0258-2724.2018.05.005XU Qingyuan, LIN Qingteng, FANG Ziyun. Theoretical study on fatigue stress spectrum of longitudinal connected slab track on brige[J]. Journal of Southwest Jiaotong University, 2018, 53(5): 906-912. doi: 10.3969/j.issn.0258-2724.2018.05.005 梁淑娟. 长大桥上CRTSⅡ型板式无砟轨道断板影响与可靠性研究[D]. 北京: 北京交通大学, 2017. 黄河山. 桥上CRTSⅡ型板式轨道假缝开裂及其影响研究[D]. 成都: 西南交通大学, 2014. 黄河山,曾毅,徐光鑫,等. 桥上CRTSⅡ型板式无砟轨道宽接缝开裂对纵连钢筋受力特性的影响[J]. 铁道标准设计,2014,58(2): 33-36.HUANG Heshan, ZENG Yi, XU Guangxin, et al. Effect on longitudinally continuous reinforcing bars' mechanical property caused by the cracking at wide juncture of CRTSⅡ slab ballastless track on bridge[J]. Railway Standard Design, 2014, 58(2): 33-36. 戴公连,葛浩,邱远喜,等. 高铁大跨度连续梁桥上无砟轨道断板受力研究[J]. 华中科技大学学报(自然科学版),2015,43(9): 100-104,109.DAI Gonglian, GE Hao, QIU Yuanxi, et al. Study on broken plate force of ballastless track on high-speed railway long-span continuous beam bridge[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2015, 43(9): 100-104,109. 钱程,沈彬然,王冠,等. 桥上无砟轨道纵连板断裂梁轨相互作用分析[J]. 铁道建筑,2016(7): 114-117. doi: 10.3969/j.issn.1003-1995.2016.07.28QIAN Cheng, SHEN Binran, WANG Guan, et al. Analysis on interaction between girder and rail under broking of ballastless track longitudinal connected slab on bridge[J]. Railway Engineering, 2016(7): 114-117. doi: 10.3969/j.issn.1003-1995.2016.07.28 陈小平,王芳芳,赵才友. 纵连底座板断裂对桥上CRTSⅡ型板式无砟轨道受力的影响[J]. 交通运输工程学报,2014,14(4): 25-35.CHEN Xiaoping, WANG Fangfang, ZHAO Caiyou. Fracture influence of longitudinal-continuous base layer on force characteristics of CRTSⅡ slab ballastless track on bridge[J]. Journal of Traffic and Transportation Engineering, 2014, 14(4): 25-35. -
下载:
点击查看大图
计量
- 文章访问数: 635
- HTML全文浏览量: 393
- PDF下载量: 22
- 被引次数: 0