协同考虑脆弱性与可靠性的城市道路网络设计

吕彪; 刘一骝; 刘海旭

doi:10.3969/j.issn.0258-2724.20180812

协同考虑脆弱性与可靠性的城市道路网络设计

doi: 10.3969/j.issn.0258-2724.20180812

基金项目: 国家自然科学基金资助项目（51278429）；教育部人文社会科学研究青年基金资助项目（18YJC630115）；中央高校基本科研业务费专项资金资助（2682018CX28）

详细信息

作者简介:
吕彪（1980—），男，讲师，博士，研究方向为交通系统优化、智能交通系统理论与方法，E-mail：swjtu_lb@126.com

中图分类号: U491
计量
- 文章访问数: 453
- HTML全文浏览量: 245
- PDF下载量: 23
- 被引次数: 0
出版历程
- 收稿日期: 2018-10-08
- 录用日期: 2018-12-21
- 修回日期: 2018-11-23
- 网络出版日期: 2019-07-10
- 刊出日期: 2019-10-01

Urban Road Network Design with Balance between Vulnerability and Reliability

摘要

摘要: 根据常态事件下出行者风险规避的路径选择行为和非常态事件下兼具风险规避与后悔规避的路径选择行为，分别以可靠性和脆弱性指标描述常态与非常态事件下的路网性能，构建了协同考虑脆弱性与可靠性的城市道路网络设计一主双从规划模型，其中上层模型为满足可靠性约束条件下的路网脆弱性指标最优（路网可达性最高），下层模型分别为基于效用理论和后悔理论的随机用户均衡模型. 算例结果表明：与仅考虑脆弱性的模型相比，本文提出的模型在牺牲一定可达性的基础上可获得较高的路网可靠性；当投资预算为0.9 × 10⁷时，平均路网可达性与路网可靠性分别为0.138 8和0.969 6，而仅考虑脆弱性的模型获得的对应指标分别为0.140 5和0.334 1，可达性指标减少了1.20%，可靠性指标增加了190.21%；此外，如果忽视出行决策行为差异，可能获得偏离实际的次优，甚至错误的网络设计方案，无法实现预期设计目标.
- 交通工程 /
- 城市道路网络设计 /
- 双层规划模型 /
- 遗传算法 /
- 后悔理论 /
- 脆弱性 /
- 可靠性
Abstract: Under normal events, travelers have route choice behaviors with risk aversion while under abnormal events, their route choice behaviors have a feature of both risk aversion and regret aversion. For this reason, an urban road network design model is constructed. It is a bilevel programming model with two lower level models in which reliability measure depicts road network performance under normal events, and vulnerability measure represents road network performance under abnormal events. The objective of the upper model is to optimize road network vulnerability measure（i.e., maximize road network accessibility measure）while it is subject to a predefined reliability constraint. The lower model include two stochastic user equilibrium models based on the utility theory and on the regret theory respectively. The results of numerical examples show that, compared with the model simply for vulnerability, the proposed model can acquire higher reliability with reduced accessibility to some extent. If investment budget is 0.9 × 10⁷, the average road network accessibility and road network reliability of the proposed model are 0.138 8 and 0.969 6 respectively, whereas as to the model simply for vulnerability, they are 0.140 5 and 0.334 1 respectively. Totally, the accessibility measure decreases by 1.20% and the reliability measure increases by 190.21%. Besides, the neglect of differences in travel decision behaviors may lead to a sub-optimal even false network design.
- traffic engineering /
- urban road network design /
- bilevel programming model /
- genetic algorithm /
- regret theory /
- vulnerability /
- reliability

HTML全文

图 1 Nguyen and Dupuis网络

Figure 1. Nguyen and Dupuis network

下载: 全尺寸图片幻灯片

表 1 路段路径关联关系

Table 1. Link-route incidence relationship

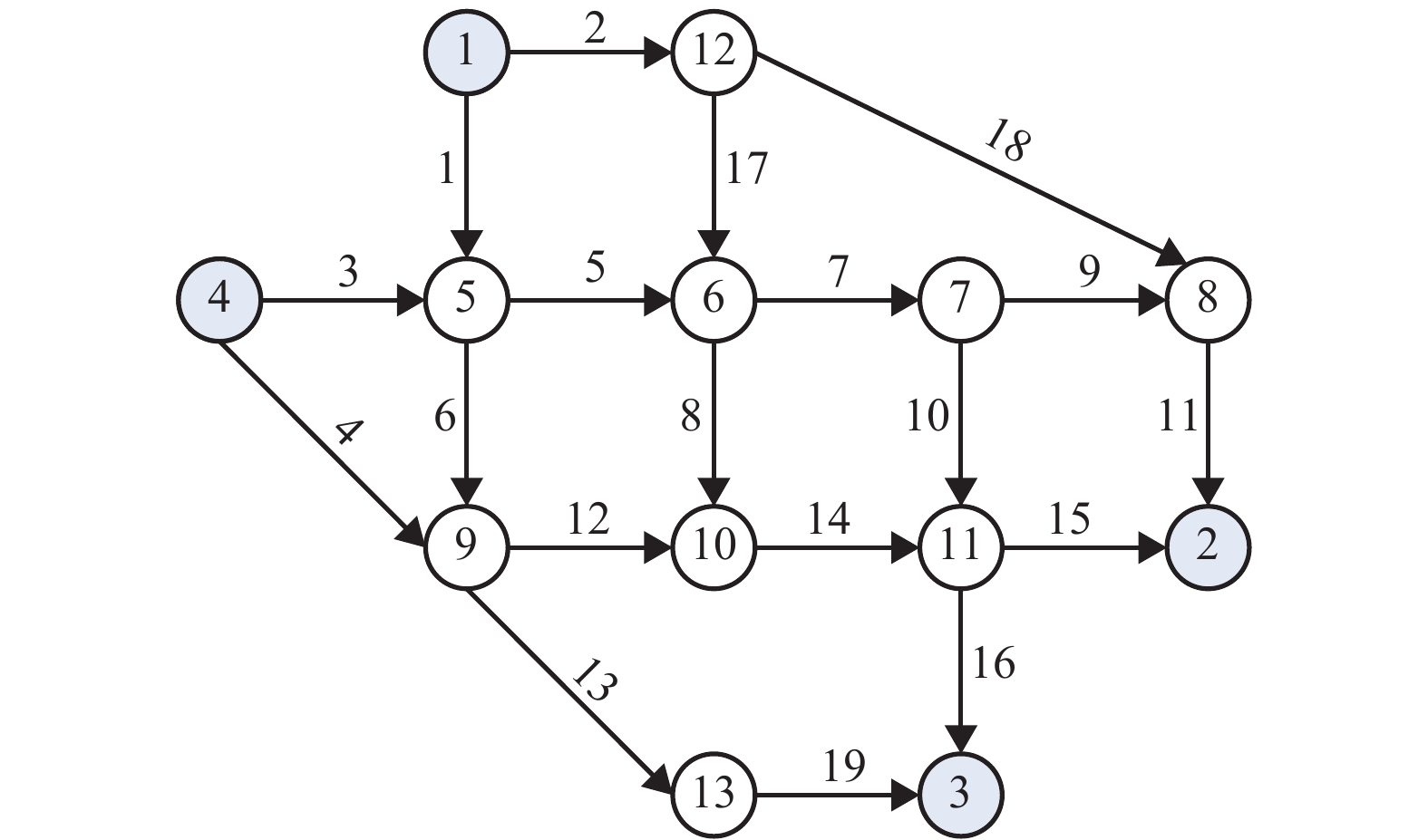
OD对	路径编号	路段序列
(1，2)	1	2→18→11
	2	2→17→7→9→11
	3	2→17→7→10→15
	4	2→17→8→14→15
	5	1→5→7→9→11
	6	1→5→7→10→15
	7	1→5→8→14→15
	8	1→6→12→14→15
(4，3)	9	3→5→7→10→16
	10	3→5→8→14→16
	11	3→6→12→14→16
	12	4→12→14→16
	13	4→13→19
	14	3→6→13→19

下载: 导出CSV

表 2 投资预算对网络设计的影响

Table 2. Effects of investment budgets on network design

变量	B = 0.8 × 10⁷		B = 0.9 × 10⁷		B = 1.0 × 10⁷
变量	协同模型	脆弱性模型	协同模型	脆弱性模型	协同模型	脆弱性模型
x₁₄	28.57	89.91	110.49	133.94	36.81	91.62
x₁₃	249.38	202.09	240.55	186.98	243.65	234.69
x₄	199.78	132.82	274.94	170.21	216.42	203.16
x₅	25.84	49.27	3.69	36.78	115.85	52.68
x₇	32.42	35.67	4.76	83.30	46.29	112.08
x₃	12.79	21.25	49.87	44.49	16.74	79.79
x₁₆	4.46	30.71	2.80	70.81	69.43	14.15
x₁₅	20.02	6.86	3.50	68.16	44.37	8.45
x₂	152.19	53.01	88.62	11.98	104.22	45.49
x₁	0.57	37.94	2.47	5.55	9.54	8.70
x₆	0.00	21.56	3.78	4.94	0.00	2.74
x₁₂	0.64	32.01	15.10	0.72	20.57	22.39
x₁₀	0.00	0.87	0.00	12.97	0.19	31.85
x₁₁	2.53	29.22	21.51	37.35	16.13	19.02
x₈	0.02	22.76	13.84	0.96	2.00	28.79
x₁₇	0.04	15.11	0.00	0.53	0.00	7.60
x₁₉	69.75	3.63	2.85	0.00	33.70	9.29
x₉	0.97	14.98	40.61	13.03	23.50	12.01
x₁₈	0.00	0.33	20.60	17.11	0.00	15.11
ψ_m，sys（x）	0.134 5	0.135 5	0.138 8	0.140 5	0.141 1	0.141 9
φ_sys（x）	0.975 8	0.455 0	0.969 6	0.334 1	0.982 9	0.749 7

下载: 导出CSV

表 4 能力扩展路段数量对网络设计的影响

Table 4. Effects of number of links with capacity enhancement on network design

变量	M = 15		M = 17		M = 19
变量	协同模型	脆弱性模型	协同模型	脆弱性模型	协同模型	脆弱性模型
x₁₄	38.25	129.36	31.54	178.38	110.49	133.94
x₁₃	232.03	151.98	230.48	274.24	240.55	186.98
x₄	228.77	142.18	244.87	125.60	274.94	170.21
x₅	25.28	53.17	49.53	38.48	3.69	36.78
x₇	30.01	103.18	68.60	33.43	4.76	83.30
x₃	33.76	87.67	18.09	22.36	49.87	44.49
x₁₆	26.53	40.40	22.30	51.48	2.80	70.81
x₁₅	31.24	48.12	13.57	24.69	3.50	68.16
x₂	114.29	41.33	127.52	34.83	88.62	11.98
x₁	27.24	7.72	23.48	35.19	2.47	5.55
x₆	6.46	17.33	0.42	11.71	3.78	4.94
x₁₂	4.70	14.75	7.26	4.21	15.10	0.72
x₁₀	26.77	21.45	13.15	4.63	0.00	12.97
x₁₁	12.56	35.02	7.79	40.15	21.51	37.35
x₈	62.03	6.00	0.72	5.39	13.84	0.96
x₁₇			27.10	3.09	0.00	0.53
x₁₉			13.11	11.71	2.85	0.00
x₉					40.61	13.03
x₁₈					20.60	17.11
ψ_m，sys（x）	0.137 2	0.139 5	0.138 5	0.140 4	0.138 8	0.140 5
φ_sys（x）	0.968 7	0.378 8	0.984 3	0.415 0	0.969 6	0.334 1

下载: 导出CSV

表 3 能力扩展方案差异对网络设计的影响(M = 15)

Table 3. Effects of differences in capacity enhancement schemes on network design (M = 15)

基于饱和度的方案			基于通行能力的方案
变量	协同模型	脆弱性模型		变量	协同模型	脆弱性模型
x₁₄	38.25	129.36		x₄	282.12	194.95
x₁₃	232.03	151.98		x₁₃	255.55	231.87
x₄	228.77	142.18		x₁	34.41	80.78
x₅	25.28	53.17		x₂	102.83	33.16
x₇	30.01	103.18		x₃	7.07	26.68
x₃	33.76	87.67		x₅	41.20	60.98
x₁₆	26.53	40.40		x₆	41.65	44.10
x₁₅	31.24	48.12		x₇	34.77	41.21
x₂	114.29	41.33		x₈	9.20	5.81
x₁	27.24	7.72		x₉	4.14	0.21
x₆	6.46	17.33		x₁₀	8.62	0.14
x₁₂	4.70	14.75		x₁₁	8.15	4.83
x₁₀	26.77	21.45		x₁₂	0.21	17.81
x₁₁	12.56	35.02		x₁₄	58.02	124.37
x₈	62.03	6.00		x₁₅	12.02	33.06
ψ_m，sys（x）	0.137 2	0.139 5		ψ_m，sys（x）	0.139 0	0.140 6
φ_sys（x）	0.968 7	0.378 8		φ_sys（x）	0.970 1	0.607 5

下载: 导出CSV

表 5 参数γ的变化对网络设计的影响

Table 5. Effects of change in coefficient γ on network design

γ	方案1		方案2		方案3
γ	ψ_m，sys (x)	φ_sys (x)	ψ_m，sys (x)	φ_sys (x)	ψ_m，sys (x)	φ_sys (x)
0.05	0.134 5	0.975 8	0.138 8	0.969 6	0.141 1	0.982 9
0.01	0.329 2	0.998 7	0.323 4	0.560 7	0.332 8	0.997 3
0.02	0.264 0	0.998 0	0.260 7	0.547 8	0.270 1	0.996 5
0.03	0.211 2	0.996 1	0.210 6	0.527 4	0.218 5	0.994 8
0.04	0.168 6	0.990	0.169 3	0.497 7	0.175 9	0.991 3
0.06	0.107 3	0.934 6	0.107 9	0.400 4	0.112 7	0.961 9
0.07	0.085 4	0.842 9	0.085 6	0.334 9	0.089 7	0.910 8

下载: 导出CSV

表 8 需求波动系数变化对网络设计的影响

Table 8. Effects of change in demand variation coefficient on network design

变量	方案1		方案2		方案3
变量	ψ_m，sys (x)	φ_sys (x)	ψ_m，sys (x)	φ_sys (x)	ψ_m，sys (x)	φ_sys (x)
ρ₀ = 50， ρ = 80	0.134 5	0.975 8	0.138 8	0.969 6	0.141 1	0.982 9
ρ₀ = 10， ρ = 30	0.135 9	1.000 0	0.140 1	1.000 0	0.142 3	1.000 0
ρ₀ = 20， ρ = 50	0.135 4	0.999 8	0.139 6	0.998 7	0.141 8	0.999 8
ρ₀ = 30， ρ = 70	0.134 8	0.997 0	0.139 1	0.992 9	0.141 3	0.998 1
ρ₀ = 60， ρ = 100	0.134 0	0.958 2	0.138 3	0.954 8	0.140 6	0.969 0
ρ₀ = 80， ρ = 120	0.133 4	0.916 0	0.137 8	0.922 1	0.140 1	0.933 0
ρ₀ = 100， ρ = 150	0.132 6	0.871 4	0.136 9	0.887 1	0.139 3	0.892 1

下载: 导出CSV

表 6 参数κ的变化对网络设计的影响

Table 6. Effects of change in coefficient κ on network design

κ	方案1		方案2		方案3
κ	ψ_m，sys (x)	φ_sys (x)	ψ_m，sys (x)	φ_sys (x)	ψ_m，sys (x)	φ_sys (x)
0.05	0.134 5	0.975 8	0.138 8	0.969 6	0.141 1	0.982 9
0.01	0.133 8	0.975 8	0.138 3	0.969 6	0.140 6	0.982 9
0.50	0.138 5	0.975 8	0.142 1	0.969 6	0.144 0	0.982 9
1.00	0.139 2	0.975 8	0.142 8	0.969 6	0.144 6	0.982 9
1.50	0.138 8	0.975 8	0.142 4	0.969 6	0.144 3	0.982 9
2.00	0.138 0	0.975 8	0.141 6	0.969 6	0.143 7	0.982 9
2.50	0.137 1	0.975 8	0.140 7	0.969 6	0.142 9	0.982 9

下载: 导出CSV

表 7 参数θ的变化对网络设计的影响

Table 7. Effects of change in coefficient θ on network design

θ	方案1		方案2		方案3
θ	ψ_m，sys (x)	φ_sys (x)	ψ_m，sys (x)	φ_sys (x)	ψ_m，sys (x)	φ_sys (x)
0.10	0.134 5	0.975 8	0.138 8	0.969 6	0.141 1	0.982 9
0.01	0.124 8	0.998 5	0.131 2	0.992 8	0.134 2	0.997 0
0.05	0.130 6	0.993 1	0.135 7	0.984 8	0.138 2	0.992 8
0.20	0.138 9	0.896 3	0.142 5	0.920 4	0.144 3	0.940 2
0.30	0.141 5	0.780 8	0.144 7	0.841 1	0.146 3	0.866 8
0.40	0.143 2	0.661 0	0.146 1	0.743 6	0.147 6	0.772 8
0.50	0.139 7	0.555 7	0.147 2	0.639 1	0.148 6	0.678 7

下载: 导出CSV

参考文献(18)

FARAHANI R Z, MIANDOABCHI E, SZETO W Y, et al. A review of urban transportation network design problems[J]. European Journal of Operational Research, 2013, 229(2): 281-302. doi: 10.1016/j.ejor.2013.01.001

CHEN A, ZHOU Z, CHOOTINAN P, et al. Transport network design problem under uncertainty: a review and new developments[J]. Transport Reviews, 2011, 31(6): 743-768. doi: 10.1080/01441647.2011.589539

CHEN A, KIM J, LEE S, et al. Models and algorithm for stochastic design problem[J]. Tsinghua Science and Technology, 2009, 14(3): 341-351. doi: 10.1016/S1007-0214(09)70050-1

NG M W, WALLER S T. Reliable system optimal network design:a convex mean-variance type model with implicit chance constraints[J]. Transportation Research Record, 2006, 1964: 81-90. doi: 10.1177/0361198106196400110

蒋洋,孙会君,吴建军. 不确定条件对交通网络设计的影响分析[J]. 交通运输系统工程与信息,2014,14(3): 85-90. doi: 10.3969/j.issn.1009-6744.2014.03.013

JIANG Yang, SUN Huijun, WU Jianjun. Comparative analysis of transportation network design problem under stochastic capacity[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(3): 85-90. doi: 10.3969/j.issn.1009-6744.2014.03.013

NIKOO N, BABAEI M, MOHAYMANY A S. Emergency transportation network design problem:identification and evaluation of disaster response routes[J]. International Journal of Disaster Risk Reduction, 2018, 27: 7-20. doi: 10.1016/j.ijdrr.2017.07.003

BEHBAHANI H, NAZARI S, KANG M J, et al. A conceptual framework to formulate transportation network design problem considering social equity criteria[J]. Transportation Research Part A, 2019, 125(7): 171-183.

BERDICA K. An introduction to road vulnerability:what has been done,is done and should be done[J]. Transport Policy, 2002(9): 117-127.

REGGIANI A, NIJKAMP P, LANZI D. Transport resilience and vulnerability:the role of connectivity[J]. Transportation Research Part A, 2015, 81: 4-15.

CHORUS C, ARENTZE T A, TIMMERMANS, H J P. A random regret minimization model of travel choice[J]. Transportation Research Part B, 2008, 42(1): 1-18. doi: 10.1016/j.trb.2007.05.004

安实,王泽,王健,等. 后悔视角下的应急疏散出行方式决策行为分析[J]. 交通运输系统工程与信息,2015,15(4): 18-23. doi: 10.3969/j.issn.1009-6744.2015.04.003

AN Shi, WANG Ze, WANG Jian, et al. Travel mode decision behavior under regret view for emergency evacuation[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(4): 18-23. doi: 10.3969/j.issn.1009-6744.2015.04.003

吕彪,刘海旭,蒲云,等. 基于累积前景理论的随机异质道路网配流模型[J]. 西南交通大学学报,2015,50(1): 173-182. doi: 10.3969/j.issn.0258-2724.2015.01.026

LÜ Biao, LIU Haixu, PU Yun, et al. Traffic assignment model based on cumulative prospect theory for stochastic road network with heterogeneous users[J]. Journal of Southwest Jiaotong University, 2015, 50(1): 173-182. doi: 10.3969/j.issn.0258-2724.2015.01.026

SHAO H, LAM W H K, TAM M L. A Reliability-based stochastic traffic assignment model for network with multiple user classes under uncertainty in demand[J]. Network and Spatial Economics, 2006, 6(3): 173-204.

FENTON L F. The sum of log-normal probability distributions in scatter transmission systems[J]. IEEE Transactions on Communications Systems, 1960, 8(1): 57-67. doi: 10.1109/TCOM.1960.1097606

黄海军. 城市交通网络平衡分析—理论与实践[M]. 北京: 人民交通出版社, 1994: 153-205

况爱武,黄中祥,况群. 随机需求道路网络出行时间可靠性评估方法[J]. 西南交通大学学报,2011,46(5): 861-867. doi: 10.3969/j.issn.0258-2724.2011.05.025

KUANG Aiwu, HUANG Zhongxiang, KUANG Qun. Evaluation method for travel time reliability of road network with stochastic demand[J]. Journal of Southwest Jiaotong University, 2011, 46(5): 861-867. doi: 10.3969/j.issn.0258-2724.2011.05.025

LUATHEP P, SUMALEE A, HO H, et al. Large-scale road network vulnerability analysis:a sensitivity analysis based approach[J]. Transportation, 2011, 38(5): 799-817. doi: 10.1007/s11116-011-9350-0

吕彪,刘海旭,蒲云. 基于遗传算法的随机路网次优拥挤收费模型[J]. 计算机工程,2013,39(8): 257-261. doi: 10.3969/j.issn.1000-3428.2013.08.056

LÜ Biao, LIU Haixu, PU Yun. Second-best congestion pricing model in a stochastic road network based on genetic algorithm[J]. Computer Engineering, 2013, 39(8): 257-261. doi: 10.3969/j.issn.1000-3428.2013.08.056

施引文献

附加材料(0)

访问统计

点击查看大图

图(1) / 表(8)

计量

文章访问数: 453
HTML全文浏览量: 245
PDF下载量: 23
被引次数: 0

协同考虑脆弱性与可靠性的城市道路网络设计

doi: 10.3969/j.issn.0258-2724.20180812

作者简介: 吕彪（1980—），男，讲师，博士，研究方向为交通系统优化、智能交通系统理论与方法，E-mail：swjtu_lb@126.com

计量

出版历程

Urban Road Network Design with Balance between Vulnerability and Reliability

计量

出版历程

目录

作者简介:
吕彪（1980—），男，讲师，博士，研究方向为交通系统优化、智能交通系统理论与方法，E-mail：swjtu_lb@126.com