Application of Multi-Clause Synergized Deduction in First-Order Logic Automated Theorem Proving
-
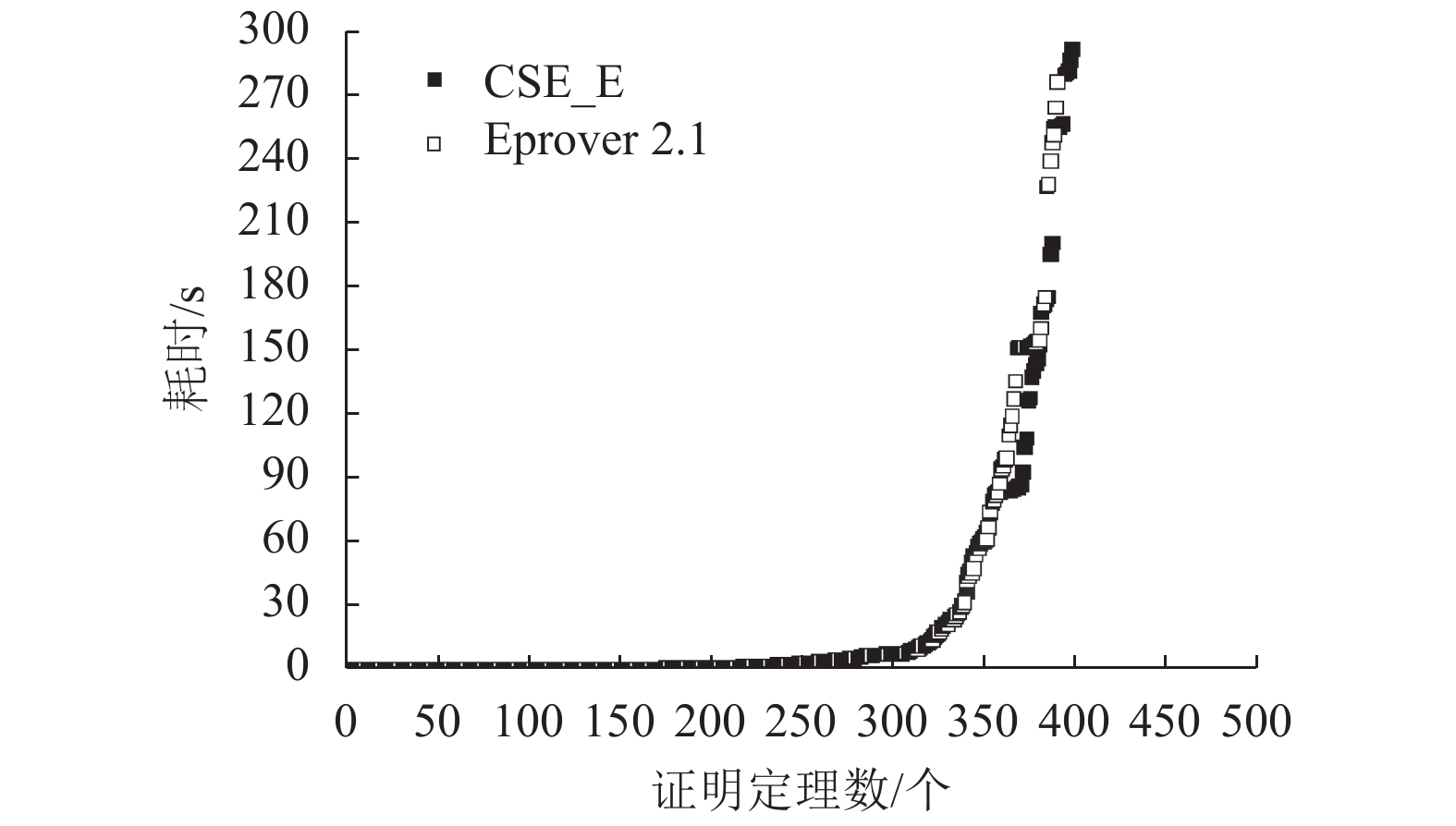
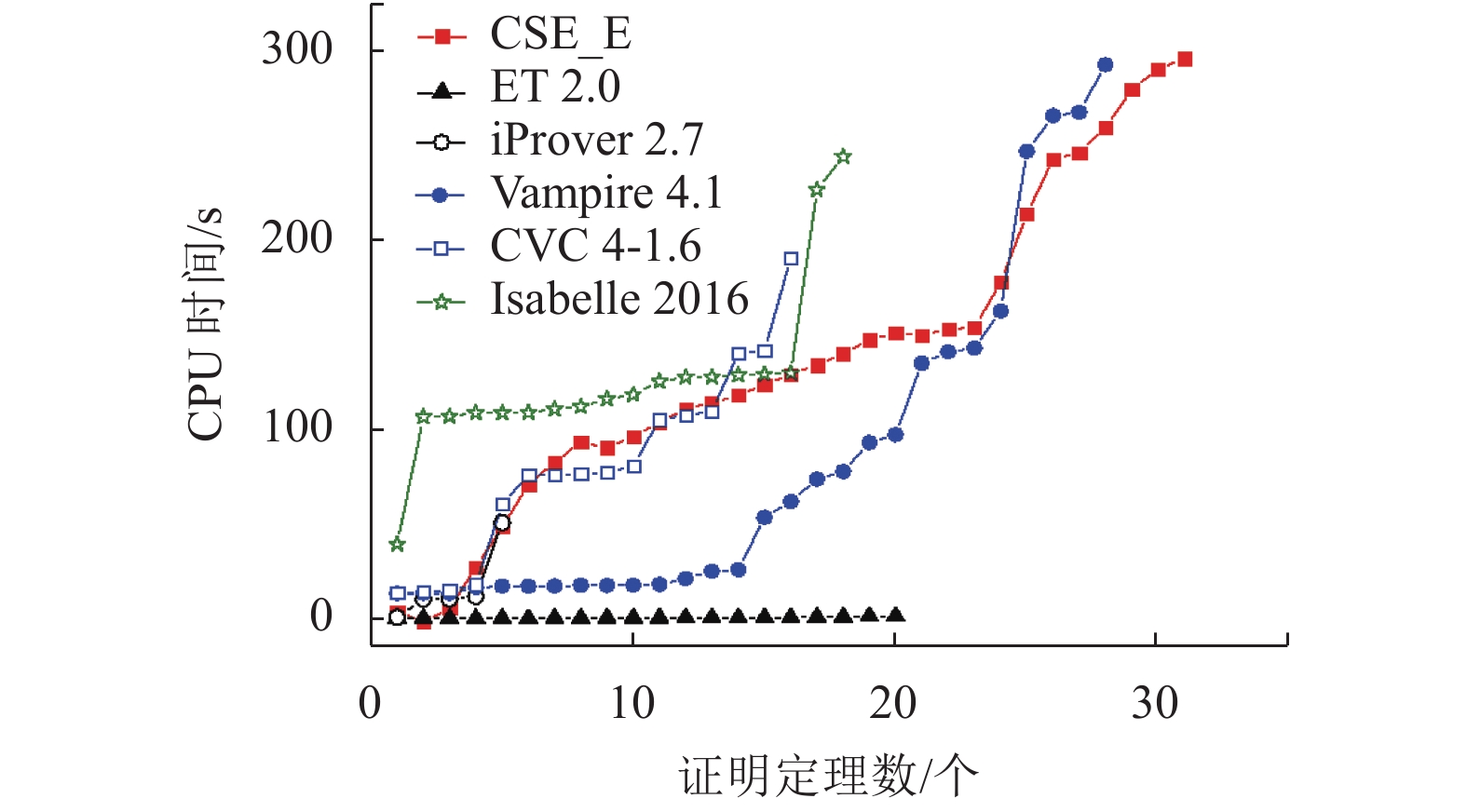
摘要: 一阶逻辑是数理逻辑中重要的分支,对其逻辑公式的自动推理是人工智能领域重要的研究热点之一. 目前一阶逻辑自动定理证明大多采用二元归结方法，每次只有2个子句进行归结，只消去1组互补对，导致演绎归结式文字数较多，影响了演绎效率. 为此，基于矛盾体分离规则提出了一种多元协同演绎算法，该算法每次允许多个子句进行协同演绎，消去多组互补对，从而演绎分离式文字数较少且可控，能有效提高推理能力；并且，该算法通过有效演绎权重和无效演绎权重调整子句演绎顺序，利用回溯机制搜索较优路径，有效规划演绎路径. 将该算法应用于国际顶尖证明器Eprover 2.1，以CADE2017竞赛例（FOF组）为测试对象，对加入多元协同演绎算法的Eprover 2.1证明器进行试验. 试验结果表明其能力超过了Eprover 2.1：多证明定理8个；能证明Eprover 2.1未证明定理31个，占未证明总数的28.2%.Abstract: First-order logic is an important branch in mathematical logic, and automated reasoning of its logical formula is one of the important research hotspots in the field of artificial intelligence. Most of the state of the art first-order logic automated theorem proving systems adopt binary resolution method. There are only two clauses involved, and therefore only a complementary pair of literals are eliminated during each resolution step. As a consequence, the resulted clause has many literals, which affects the deduction efficiency. In this paper, a multi-clause synergized deduction algorithm is proposed based on contradiction separation rule. This algorithm allows multiple clauses used in deduction, and is able to eliminate more than one complementary pairs. The clause of contradiction separation is controllable and usually has less literals, which can effectively improve the inference ability. This multi-clause synergized algorithm adjusts the deduction order of clauses according to two kinds of weights, effective deduction weight and ineffective deduction weight. Backtracking mechanism is used to search for an optimal path, and effectively plan the deduction path. The algorithm is applied to the international top prover－Eprover 2.1, and Conference on Automated Deduction 2017 competition theorems (FOF division) are set as the test object. Eprover 2.1 with multi-clause synergized deduction algorithm outperformed Eprover 2.1 and solved 8 theorems more than Eprover 2.1. It also solved 31 theorems out of the 110 theorems unsolved by Eprover 2.1, accounting for 28.2% of the total.
-
图 2 CSE_E与Eprover 2.1证明定理时间与个数分布
Figure 2. Distribution graph of time and the number of solved theorems by CSE_E and Eprover 2.1
表 1 CSE_E与Eprover 2.1在不同难度系数下证明定理数量对比
Table 1. Numbers of solved theorems byCSE_E and Eprover 2.1 with different ratings
证明器 0 ≤ R < 0.5 0.5 ≤ R < 0.6 0.6 ≤ R < 0.7 CSE_E 221 59 31 Eprover 2.1 221 57 30 证明器 0.7 ≤ R < 0.8 0.8 ≤ R < 0.9 0.9 ≤ R < 1.0 CSE_E 56 27 4 Eprover 2.1 51 26 5 
下载: 导出CSV
表 2 CSE_E证明的31个定理判定情况
Table 2. Details of 31 theorems solved by CSE_E
定理名称 难度等级 子句数 最大文字数 证明时间/s 定理名称 难度等级 子句数 最大文字数 证明时间/s AGT011+2 0.86 923 8 224.760 LCL658+1.005 0.50 2 32 243.104 BOO109+1 0.67 3 6 60.036 LCL658+1.010 0.50 2 40 293.124 GEO090+1 0.79 17 12 133.250 LCL660+1.001 0.33 2 37 163.852 GEO491+1 0.90 45 22 108.680 SCT143+1 0.76 523 19 114.688 GEO495+1 0.79 68 22 90.124 SCT170+2 0.90 1 012 18 160.340 GEO502+1 0.55 126 22 2.680 SET672+3 0.90 29 13 151.700 GEO506+1 0.83 143 22 91.316 SWB010+1 0.90 560 27 119.477 GEO507+1 0.62 144 22 91.364 SWB025+1 0.72 560 27 6.156 GEO511+1 0.90 162 22 150.176 SWB027+1 0.79 560 27 60.076 GEO517+1 0.79 181 30 150.144 SWB070+1 0.90 560 27 108.263 GEO521+1 0.97 195 30 138.144 SWB081+1 0.79 560 27 121.108 GEO531+1 0.66 222 31 132.076 SWB093+1 0.79 560 27 1.530 GEO532+1 0.76 223 31 150.228 SWB104+1 0.83 560 27 20.080 GEO536+1 0.86 229 31 244.877 SWW100+1 0.79 45 10 256.170 LAT306+2 0.97 2 959 27 294.385 SYN938+1 0.17 1 55 283.660 SYO525+1.021 0.67 30 28 92.556
下载: 导出CSV
-
PAVLOV V, SCHUKIN A, CHERKASOVA T. Exploring automated reasoning in first-order logic:tools,techniques and application areas[J]. Communications in Computer & Information Science, 2013, 394(1): 102-116. DAVIS M. The early history of automated deduction[J]. Handbook of Automated Reasoning, 2002, 714(3): 5-15. PLAISTED D A. History and prospects for first-order automated deduction[C]//Proceedings of 25th International Conference on Automated Deduction. Cham: Springer, 2015: 3-28. ROBINSON J A. The generalized resolution principle[M]//SIEKMANN J, WRIGHTSON G. Automation of Reasoning-3. Berlin Heidelberg: Springer International Publishing, 1983: 135-151. RUBIN N, HARRISON M C. Another generalization of resolution[J]. Journal of the Association for Computing Machinery, 1978, 25(3): 341-351. doi: 10.1145/322077.322078 LU Ruzhan, LIN Kai, SUN Yongqiang. Colored resolution,pi-colored clash and its completeness[J]. Journal of Computer, 1987, 12: 18-25. LOVELAND D W. A linear format for resolution[C]//Symposium on Automatic Demonstration. Berlin: Springer, 1970: 147-162. LUCKHAM D. Refinements in resolution theory[C]//Symposium on Automatic Demonstration. Berlin: Springer, 1970: 163-190. OVERBEEK R, MCCHAREN J, WOS L. Complexity and related enhancements for automated theorem-proving programs[J]. Computers & Mathematics with Applications, 1976, 2(1): 1-16. ROBINSON J A. Automatic deduction with hyper-resolution[J]. International Journal of Computing & Mathematics, 1965, 1(3): 227-234. SLANEY J, PALEO B W. Conflict resolution:a first-order resolution calculus with decision literals and conflict-driven clause learning[J]. Journal of Automated Reasoning, 2016, 12(4): 1-24. RIAZANOV A, VORONKOV A. The design and implementation of vampire[J]. Ai Communications, 2002, 15(2): 91-110. VORONKOV A. First-order theorem proving and vampire[C]//Proceedings of International Conference on Computer Aided Verification. Berlin: Springer-Verlag, 2013: 1-35. SCHULZ S. E-a brainiac theorem prover[J]. AI Com- munications, 2002, 15(2): 111-126. SCHULZ S. System description: E 1.8[C]//Proceedings of 19th International Conference on Logic for Programming, Artificial Intelligence, and Reasoning. Berlin: Springer-Verlag, 2013: 735-743. BAUMGARTNER P, BAX J, WALDMANN U. Beagle－a hierarchic superposition theorem prover[C]// Proceedings of 25th International Conference on Automated Deduction. Cham: Springer, 2015: 367-377. WEIDENBACH C, BRAHM U, HILLENBRAND T, et al. Spass version 2.0[C]//Proceedings of International Conference on Automated Deduction. Berlin: Springer-Verlag, 2002: 275-279. VORONKOV A. AVATAR: The architecture for first-order theorem provers[C]//Proceedings of International Conference on Computer Aided Verification. Cham: Springer, 2014: 696-710. DENZINGER J, KRONENBURG M, SCHULZ S. DISCOUNT-a distributed and learning equational prover[J]. Journal of Automated Reasoning, 1997, 18(2): 189-198. doi: 10.1023/A:1005879229581 MCCUNE W, WOS L. Otter-the CADE-13 competition incarnations[J]. Journal of Automated Reasoning, 1997, 18(2): 211-220. doi: 10.1023/A:1005843632307 REGER G, TISHKOVSKY D, VORONKOV A. Cooperating proof attempts[C]//Proceedings of 25th International Conference on Automated Deduction. Cham: Springer, 2015: 339-355. SCHULZ S, MOHNMANN M. Performance of clause selection heuristics for saturation-based theorem proving[C]//Proceedings of 8th International Joint Conference. Cham: Springer, 2016: 330-345. HODER K, REGER G, SUDA M, et al. Selecting the selection[C]//Proceedings of 8th International Joint Conference on Automated Reasoning. Cham: Springer, 2016: 313-329. XU Yang, LIU Jun, CHEN Shuwei, et al. Contradiction separation based dynamic multi-clause synergized automated deduction[J]. Information Sciences, 2018, 462(5): 93-113. XU Yang, LIU Jun, CHEN Shuwei, et al. Distinctive features of the contradiction separation based dynamic automated deduction[C]//Proceedings of 13th International FLINS Conference on Decision Making and Soft Computing. Belfast: World Scientific, 2018: 725-732. SUTCLIFFE.G.The 7th IJCAR automated theorem proving system competition-CASC-J7[J]. AI Communications, 2015, 28(4): 683-692. doi: 10.3233/AIC-150668 SUTCLIFFE.G.The 8th IJCAR automated theorem proving system competition-CASC-J8[J]. AI Communications, 2016, 29(5): 607-619. doi: 10.3233/AIC-160709 -
下载:
点击查看大图
图(3) / 表(2)
计量
- 文章访问数: 569
- HTML全文浏览量: 270
- PDF下载量: 14
- 被引次数: 0