Parameters Quantification of Forchheimer Equation and Critical Point of Transition from Darcian to Non-Darcian Flow
-
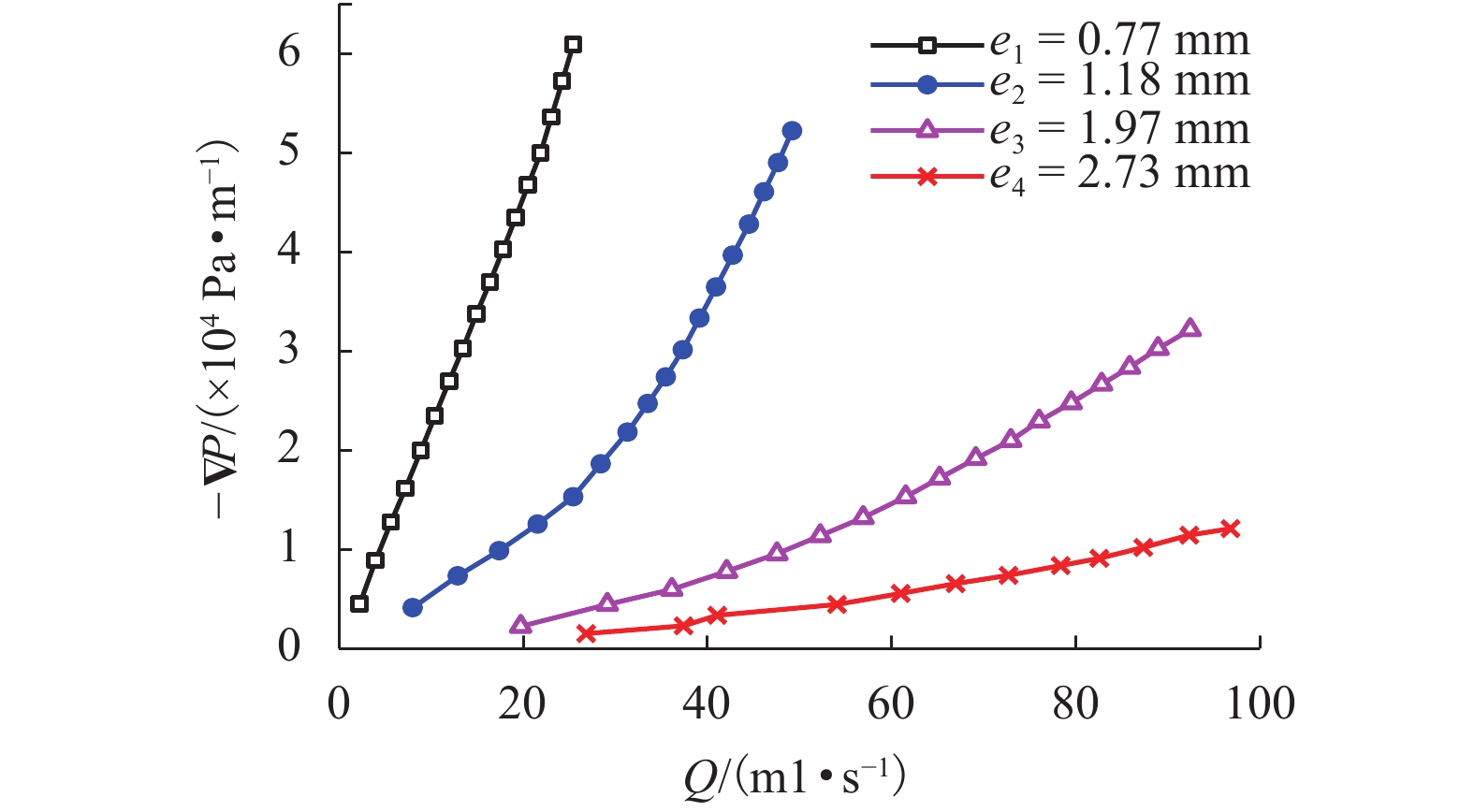
摘要: 为探究岩体裂隙中水流的运动规律，基于真实岩体材料建立裂隙渗流模型，对裂隙中的渗流状态及渗流参数进行了研究. 区别于水泥、玻璃、亚克力、钢材等常见非石材类材质，选用天然大理石岩块为基材构建单裂隙渗流模型，开展不同隙宽（0.77、1.18、1.97、2.73 mm）的渗流试验，考察压力损失与流量的关系，探讨达西—非达西流转变的临界点及Forchheimer方程的参数量化问题. 研究结果表明：隙宽为0.77 mm时压力梯度与流量基本呈线性达西关系，随着隙宽和流量的增大，二者呈现出明显的非达西特征，可用Forchheimer方程描述；Forchheimer方程的粘滞项和惯性系数均可表达为隙宽的幂函数，引入雷诺数对惯性项系数进行修正可以减少误差；提出以压力梯度-流量曲线的斜率变化特征来判断达西—非达西流临界点的方法，并在本试验中得到了验证.
-
关键词:
- 裂隙 /
- 非达西 /
- Forchheimer方程 /
- 雷诺数 /
- 临界点
Abstract: In order to explore the movement law of water flow in rock mass fissures, a fracture seepage flow model was established with real rock mass materials to study the seepage flow state and parameters. The single-fracture seepage flow model was constructed using natural marble blocks, instead of the common non-stone materials such as cement, glass, acrylic, and steel. Based on the model, seepage experiments with different fissure widths (0.77, 1.18, 1.97, 2.73 mm) were conducted to investigate the relationship between pressure loss and flow rate, the critical point of transition from Darcian to non-Darcian flow, and the quantification of parameters in the Forchheimer equation. Results show that the relationship between pressure gradient and flow rate is governed by linear Darcy’s law when the fracture width is 0.77 mm, but obvious non-Darcy characteristics are observed with the increase of the fracture width and flow rate, which can be described by Forchheimer equation. The coefficient of viscosity and inertia term of the Forchheimer equation can be expressed as a power function of fracture width, and the error can be reduced by introducing Reynolds number to correct the inertia coefficient. Besides, the method of judging the critical point of transition from Darcian to non-Darcian flow via the slope characteristics of pressure gradient-flow curve proved feasible in this experiment.-
Key words:
- fracture /
- non-Darcy /
- Forchheimer equation /
- Reynolds number /
- critical point
-
图 3 实验值与计算值（
$- \nabla {P_{1i}} $ ）比较Figure 3. Comparison between experimental value and calculated value (
$ - \nabla {P_{1i}} $) 
图 4
$ - \nabla {P_{1i}} $ 相对误差分布Figure 4. Relative error distribution of model
$ - \nabla {P_{1i}} $ 
图 5 试验值与计算值（
$ - \nabla {P_{2i}}$ ）比较Figure 5. Comparison between experimental value and calculated value (
$- \nabla {P_{2i}} $ )
图 6
$- \nabla {P_{2i}} $ 相对误差分布Figure 6. Relative error distribution of model
$- \nabla {P_{2i}} $ 表 1 压力梯度与流量的拟合关系式
Table 1. Fitted formulas between pressure gradient and flow rate
类别 隙宽/mm 拟合方程 R2 线性方程 0.77 $ { {\rm{ - } }\nabla P_1 = 22.539\;6Q}$ 0.997 3 1.18 $ { {\rm{ - } }\nabla P_2 = 8.793\;7Q}$ 0.879 3 1.97 $ { {\rm{ - } }\nabla P_3 = 2.918\;2Q}$ 0.864 9 2.73 $ { {\rm{ - } }\nabla P_4 = 1.079\;3Q}$ 0.887 1 Forchheimer方程 0.77 $ { {\rm{ - } }\nabla P_1 = 20.722\;7Q + 0.090\;8{Q^2} }$ 0.999 1 1.18 $ { {\rm{ - } }\nabla P_2 = 1.739\;6Q + 0.176\;1{Q^2} }$ 0.995 6 1.97 $ { {\rm{ - } }\nabla P_3 = 0.477\;7Q + 0.032\;9{Q^2} }$ 0.999 6 2.73 $ { {\rm{ - } }\nabla P_4 = 0.310\;9Q + 0.009\;8{Q^2} }$ 0.997 3 
下载: 导出CSV
表 2
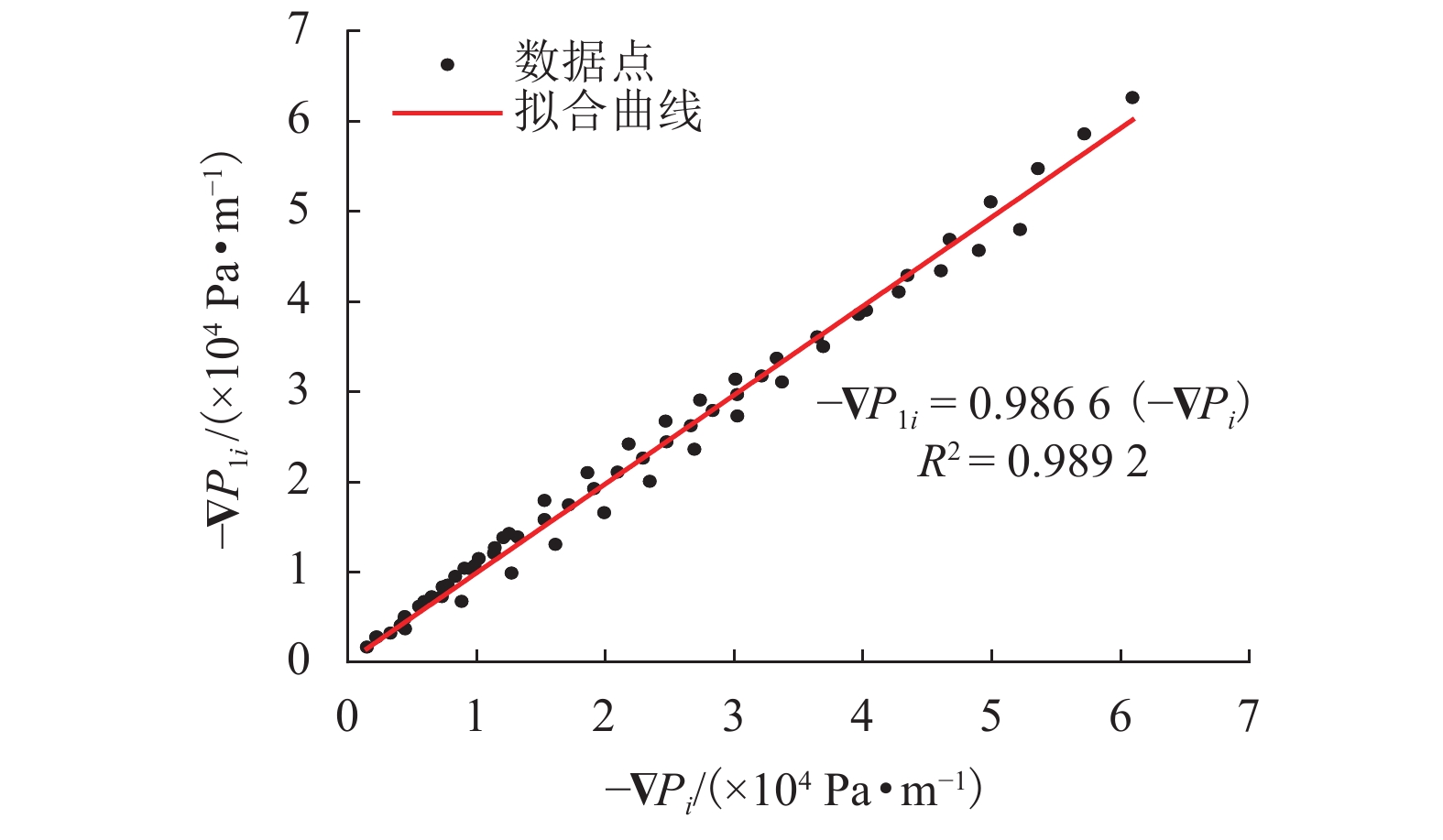
$ - \nabla {P_{{\rm{1}}i}}$ 模型参数计算结果Table 2. Calculated parameters of model
$ - \nabla {P_{{\rm{1}}i}}$ c1 n1 c2 n2 6.848 4 −3.091 1 0.177 1 −2.718 7
下载: 导出CSV
表 3
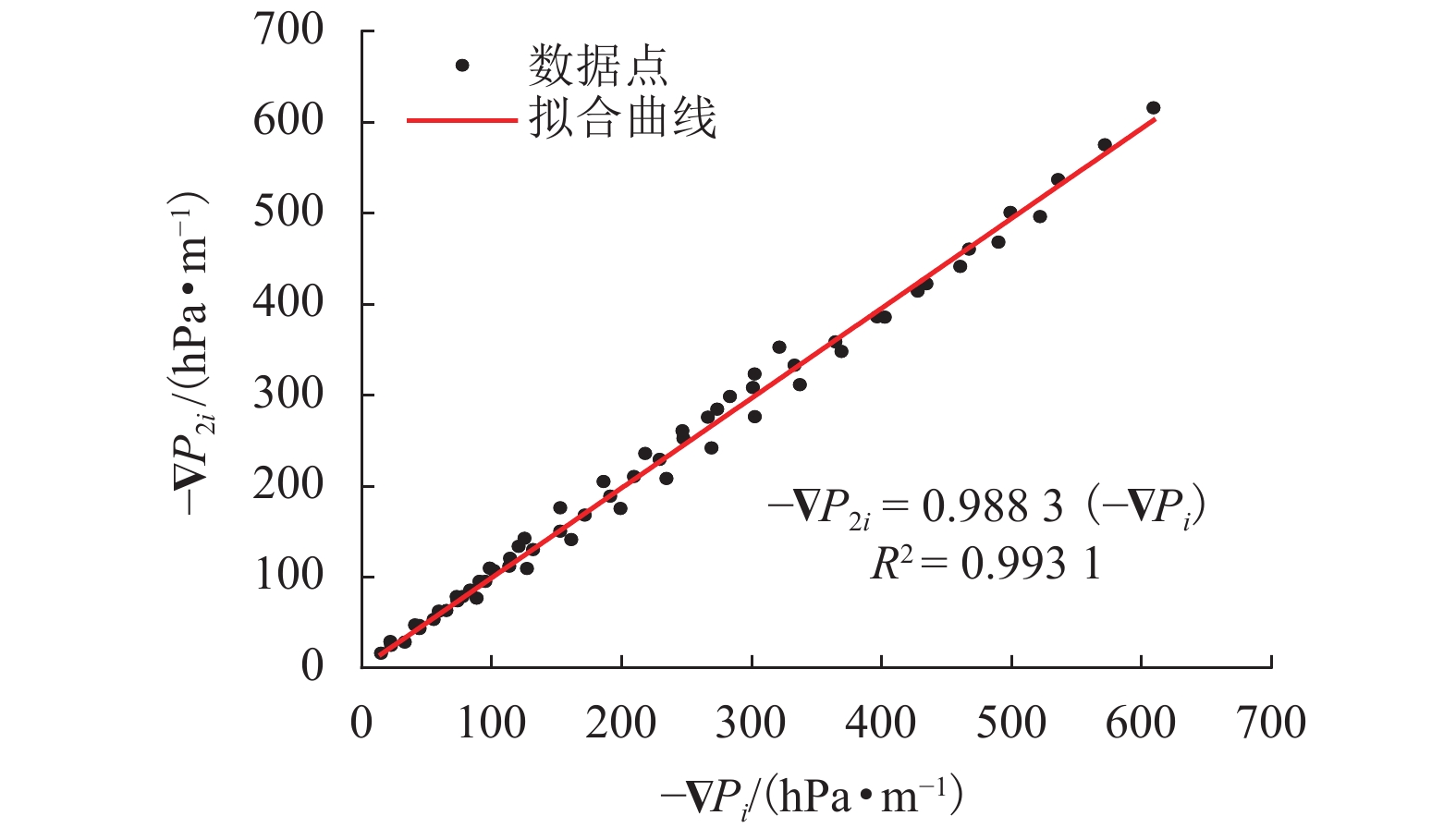
$ - \nabla {P_{{\rm{2}}i}}$ 模型参数计算结果Table 3. Calculated parameters of model
$ - \nabla {P_{{{\rm{2}}i}}}$ c3 n3 c4 n4 9.112 2 −2.819 1 0.000 12 −3.452 6
下载: 导出CSV
表 4 不同隙宽的临界流量及雷诺数
Table 4. Values of critical flux and critical Reynolds number for different fracture widths
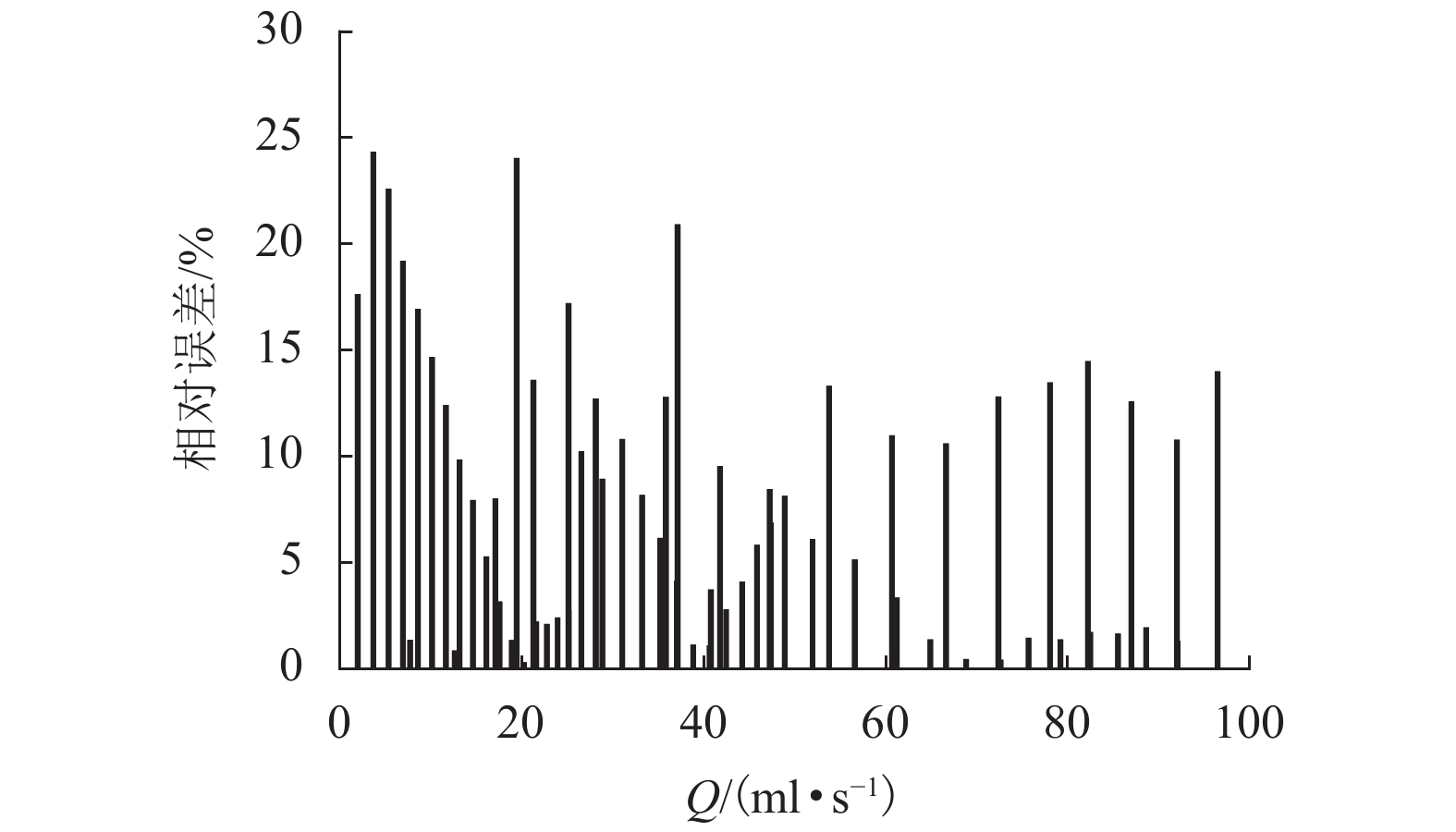
隙宽/mm ${E_{P{_ {i} } } }$/% 临界流量/（ml•s−1） 临界雷诺数 0.77 18 23.07 614.55 1.18 20 28.44 741.30 1.97 28 42.11 1 054.30 2.73 33 54.09 1 304.72
下载: 导出CSV
-
闻德荪. 工程流体力学: 水力学[M]. 3版. 北京: 高等教育出版社, 2010: 225-228. 赵延林. 裂隙岩体流固耦合响应与工程应用[M]. 北京: 科学出版社, 2016: 14-21. LOMIZE G M. Flow in fractured rocks[M]. Moscow: Gosenergoizdat, 1951: 27. 王媛,速宝玉. 单裂隙面渗流特性及等效水力隙宽[J]. 水科学进展,2002,13(1): 61-68. doi: 10.3321/j.issn:1001-6791.2002.01.011WANG Yuan, SU Baoyu. Research on the behavior of fluid flow in a single fracture and its equivalent hydraulic apecture[J]. Advances in Water Science, 2002, 13(1): 61-68. doi: 10.3321/j.issn:1001-6791.2002.01.011 ZHANG Zhenyu, NEMCIK J, QIAO Qiuqiu, et al. A model for water flow through rock fractures based on friction factor[J]. Rock Mechanics & Rock Engineering, 2015, 48(2): 559-571. QIAN Jiazhong, CHEN Zhou, ZHAN Hongbin, et al. Experimental study of the effect of roughness and Reynolds number on fluid flow in rough-walled single fractures:a check of local cubic law[J]. Hydrological Processes, 2011, 25(4): 614-622. CHERUBINI C, GIASI C I, PASTORE N. Bench scale laboratory tests to analyze non-linear flow in fractured media[J]. Hydrology & Earth System Sciences, 2012, 9(4): 2511-2522. SIDIROPOULOU M G, MOUTSOPOULOS K N, TSIHRINTZIS V A. Determination of Forchheimer equation coefficients a and b[J]. Hydrological Processes, 2007, 21(4): 534-554. doi: 10.1002/hyp.6264 JOHNSON J, BROWN S, STECKMAN H. Fluid flow and mixing in rough-walled fracture intersections[J]. Journal of Geophysical Research Solid Earth, 2006, 111: 1-16. QIAN Jiazhong, ZHAN Hongbin, LUO Shaohe, et al. Experimental evidence of scale-dependent hydraulic conductivity for fully developed turbulent flow in a single fracture[J]. Journal of Hydrology, 2007, 339(3): 206-215. ZHANG Zhenyu, NEMCIK J. Fluid flow regimes and nonlinear flow characteristics in deformable rock fractures[J]. Journal of Hydrology, 2013, 477(1): 139-151. ZOU Liangchao, JING Lanru, CVETKOVIC V. Roughness decomposition and nonlinear fluid flow in a single rock fracture[J]. International Journal of Rock Mechanics & Mining Sciences, 2015, 75: 102-118. QIAN Jiazhong, WANG Mu, ZHANG Yong, et al. Experimental study of the transition from non-Darcian to Darcy behavior for flow through a single fracture[J]. Journal of Hydrodynamics, 2015, 27(5): 679-688. doi: 10.1016/S1001-6058(15)60530-3 QUINN P M, CHERRY J A, PARKER B L. Quantification of non-Darcian flow observed during packer testing in fractured sedimentary rock[J]. Water Resources Research, 2011, 47(9): 1-15. 刘日成,李博,蒋宇静,等. 等效水力隙宽和水力梯度对岩体裂隙网络非线性渗流特性的影响[J]. 岩土力学,2016,37(11): 3165-3174.LIU Richeng, LI Bo, JIANG Yujing, et al. Effects of equivalent hydraulic aperture and hydraulic gradient on nonlinear seepage properties of rock mass fracture networks[J]. Rock and Soil Mechanics, 2016, 37(11): 3165-3174. CHEN Yifeng, ZHOU Jiaqing, HU Shaohua, et al. Evaluation of Forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures[J]. Journal of Hydrology, 2015, 529: 993-1006. doi: 10.1016/j.jhydrol.2015.09.021 刘咏, 钱家忠, 赵卫东. 窄缝裂隙水流雷诺数的实验研究[C]//第七届全国水动力学学术会议暨第十九届全国水动力学研讨会文集（上册）. 上海: 海洋出版社, 2005: 475-480 刘丽红,吴潇潇,颜冰. 岩块尺度达西流非达西流流态转化研究[J]. 科技通报,2017,33(1): 32-38.LIU Lihong, WU Xiaoxiao, YAN Bing. Research of transition between the Darcian and non-Darcian flow of rock block scale[J]. Bulletin of Science and Technology, 2017, 33(1): 32-38. 郭建春,庄园,刘超. 考虑非达西效应的酸蚀裂缝流场数值模拟[J]. 岩土力学,2015,36(11): 3315-3321.GUO Jianchun, ZHUANG Yuan, LIU Chao. Numerical simulation of flow field of acid etched fractures considering non-Darcy effect[J]. Rock and Soil Mechanics, 2015, 36(11): 3315-3321. ZIMMERMAN R W, AL-YAARUBI A, PAIN C C, et al. Non-linear regimes of fluid flow in rock fractures[J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(3): 384-384. FORCHHEIMER P H. FORCHHEIMER P H. Wasserbewegung durch Boden[J]. Zeitschrift des Vereines Deutscher Ingeneieure, 1901, 45: 1782-1788. 李加武,崔欣,张宏杰,等. 粗糙度对雷诺数效应的影响[J]. 长安大学学报(自然科学版),2009,29(2): 56-59.LI Jiawu, CUI Xin, ZHANG Hongjie, et al. Influence of surface roughness on Reynolds number effects[J]. Journal of Chang ’an University ( Natural Science Edition), 2009, 29(2): 56-59. SCHRAUF T W, EVANS D D. Laboratory studies of gas flow through a single natural fracture[J]. Water Resour. Res., 1986, 22(7): 1038-1050. doi: 10.1029/WR022i007p01038 ZIMMERMAN R W, BODVARSSON G S. Hydraulic conductivity of rock fractures[J]. Transport in Porous Media, 1996, 23(1): 1-30. NOWAMOOZ A, RADILLA G, FOURAR M. Non-Darcian two-phase flow in a transparent replica of a rough-walled rock fracture[J]. Water Resources Research, 2009, 45(7): W07406. TZELEPIS V, MOUTSOPOULOS K N, PAPASPYROS J N E, et al. Experimental investigation of flow behavior in smooth and rough artificialfractures[J]. Journal of Hydrology, 2015, 521: 108-118. doi: 10.1016/j.jhydrol.2014.11.054 王潇. 单裂隙中粗糙元及其疏密度对水流特性影响模拟研究[D]. 合肥: 合肥工业大学, 2014. ZENG Zhengwen, GRIGG R. A criterion for non-Darcy flow in porous media[J]. Transport in Porous Media, 2006, 63(1): 57-69. doi: 10.1007/s11242-005-2720-3 MACINI P, MESINI E, VIOLA R. Laboratory measurements of non-Darcy flow coefficients in natural and artificial unconsolidated porous media[J]. Journal of Petroleum Science and Engineering, 2011, 77(3): 365-374. -
下载:
点击查看大图
图(7) / 表(4)
计量
- 文章访问数: 553
- HTML全文浏览量: 756
- PDF下载量: 75
- 被引次数: 0