Homogeneous Generalized Yield Function for Frame Members with Box Section
-
摘要: 为了克服传统广义屈服函数的局限性，建立了适用于平面和空间框架结构，且对截面几何尺寸不敏感的箱型构件通用齐次广义屈服函数，提出了箱型框架极限承载力分析的高效线弹性迭代方法. 首先，通过对比分析遴选出对截面几何参数不敏感的箱型截面广义屈服函数作为基准；然后，根据全面试验法确定了拟合配点，并通过回归分析建立了考虑轴力和双向弯矩联合作用的箱型截面通用齐次广义屈服函数；最后，结合弹性模量缩减策略，提出了箱型截面框架结构极限承载力分析的高效线弹性迭代方法. 研究结果表明：建立的箱型截面通用齐次广义屈服函数不仅克服了普通广义屈服函数计算结果不稳定的缺陷，而且克服了现存齐次广义屈服函数存在的对截面几何尺寸敏感且不适用于空间结构等问题；建立的结构极限承载力分析的方法较传统的弹塑性增量分析法相对误差不超过3%，且计算时间不足传统分析法的10%，均表明本文建立方法的精确性和适用性.Abstract: In order to overcome limitations of the traditional generalized yield function (GYF), a homogeneous generalized yield function (HGYF) is proposed for box sections, which is insensitive to sectional geometry of box sections and applicable for plane and spatial frame structures; and a linear-elastic iterative method with higher efficiency is presented for ultimate bearing capacity of framed structures. Firstly, different generalized yield functions (GYF) are investigated and the suitable one is selected as insensitive to the geometric parameters of box sections. Then a set of fitting points are determined according to the comprehensive test method, based on which an HGYF was developed by regression analysis with a wide range of application for box sections. Finally, a linear-elastic iterative method is presented with high efficiency for the ultimate bearing capacity of frames with box section on the basis of elastic modulus reduction method (EMRM). Numerical examples show that the proposed HGYF achieves satisfying stable results with a wide range of application for plane and spatial frames, overcoming not only the instability of the traditional GYF, but also the sensitivity of the existing HGYF to geometry of sections which is unsuitable for spatial frames. The relative error of the established method is less than 3% compared with the traditional elasto-plastic incremental analysis method, and the calculation time is less than 10% that of the traditional analysis method, which shows the accuracy and efficiency of this method.
-
图 4 基于fZ和
${\bar f_4}$ 的EMRM迭代过程Figure 4. Iterative process of the EMRM based on
${f_{\rm{Z}}}\;{\rm{\& }}\;{\bar f_4}$ 
图 6 基于fZ和
${\bar f_4}$ 的EMRM迭代计算过程Figure 6. Iterative process of the EMRM based on
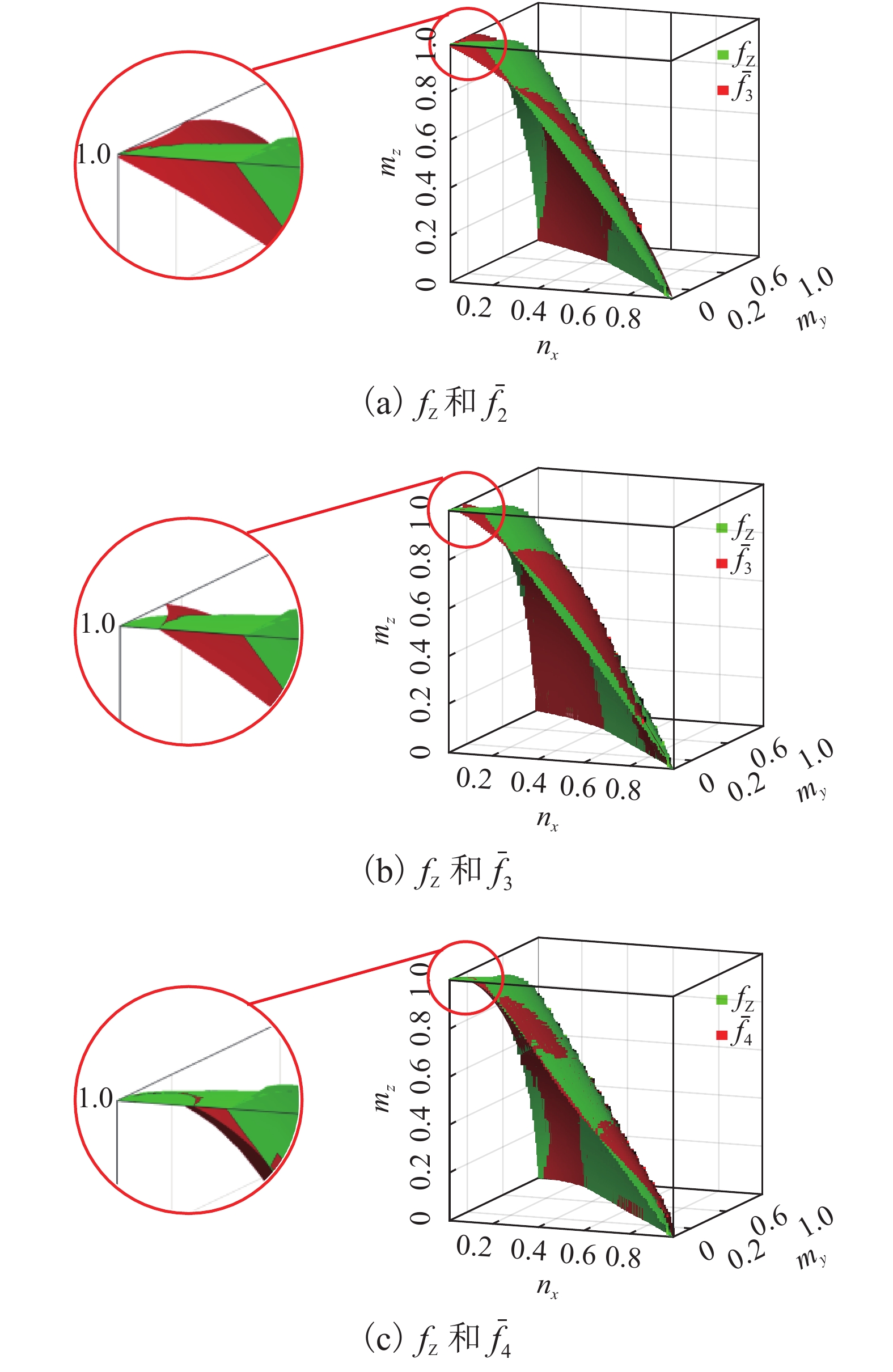
${f_{\rm{Z}}}\;{\rm{\& }}\;{\bar f_4}$ 表 1 残差均方差
Table 1. Residual mean-square deviation
${{\bar f}_2}$ ${{\bar f}_3}$ ${{\bar f}_4}$ 0.068 0.057 0.042 
下载: 导出CSV
表 3 不同方法计算结果的收敛性分析
Table 3. Convergences of the results from different methods
计算方法 文献 参数 构件离散单元数 2 3 4 6 8 10 12 EMRM 本文HGYF 极限承载力/(kN•m−1) 60.53 59.27 60.09 59.65 相对差/% 2.08 1.34 0.73 计算时间/s 7.4 11.2 13.7 19.6 文献[15] HGYF 极限承载力/（kN•m−1） 58.65 57.29 57.99 57.58 相对差/% 2.32 1.22 0.71 计算时间/s 13.3 15.9 19.0 20.6 EPIA 极限承载力/（kN•m−1） 75.76 69.47 66.48 63.83 62.56 61.74 61.37 相对差/% 8.30 4.30 3.99 1.99 1.31 0.60 计算时间/s 12.0 17.2 18.8 24.9 37.4 43.2 48.6
下载: 导出CSV
表 4 荷载初值对结构极限承载力的影响
Table 4. Influence of the initial load on ultimate bearing capacity
计算方法 文献 荷载初值/
（kN•m−1）极限荷载/
（kN•m−1）计算
时间/s相对
误差/%EPIA 61.74 43.2 EMRM GYF[6] 30 93.36 15.3 51.21 60 56.95 12.8 7.76 120 27.47 11.8 55.51 GYF[7] 30 80.12 9.7 29.77 60 51.10 8.9 17.23 120 28.97 9.3 53.08 GYF[8] 30 64.08 17.7 3.79 60 37.27 15.6 39.63 120 18.81 14.9 69.53 本文HGYF 30 60.09 17.3 2.67 60 60.09 17.6 2.67 120 60.09 16.5 2.67
下载: 导出CSV
表 5 几何参数
Table 5. Geometry parameters
$\beta $ 截面参数/m 梁 柱 $\gamma = 5$ $\gamma = 10$ $\gamma = 5$ $\gamma = 10$ $ 1.0$ b 0.10 0.10 0.20 0.20 h 0.10 0.10 0.20 0.20 t1 0.02 0.01 0.04 0.02 t2 0.02 0.01 0.04 0.02 $ 1.5$ b 0.10 0.10 0.20 0.20 h 0.15 0.15 0.30 0.30 t1 0.03 0.015 0.06 0.03 t2 0.01 0.01 0.04 0.02 $2.0$ b 0.10 0.10 0.20 0.20 h 0.20 0.20 0.40 0.40 t1 0.04 0.02 0.08 0.04 t2 0.02 0.01 0.04 0.02
下载: 导出CSV
表 6
$\gamma $ 和$\beta $ 对计算结果的影响Table 6. Influence of
$\gamma $ and$\beta $ on the results计算方法 文献 $\beta $ $\gamma $ 极限荷载/
（kN•m−1）相对误差/% EPIA 1.0 5 31.44 10 19.49 1.5 5 70.19 10 42.25 2.0 5 137.96 10 81.02 EMRM 本文
HGYF1.0 5 30.67 2.45 10 19.07 2.15 1.5 5 68.72 2.09 10 41.44 1.92 2.0 5 134.91 2.21 10 79.24 2.20 文献[17]
HGYF1.0 5 30.21 3.91 10 18.75 3.80 1.5 5 66.54 5.20 10 40.06 5.18 2.0 5 127.02 7.93 10 74.46 8.10
下载: 导出CSV
表 7 几何尺寸
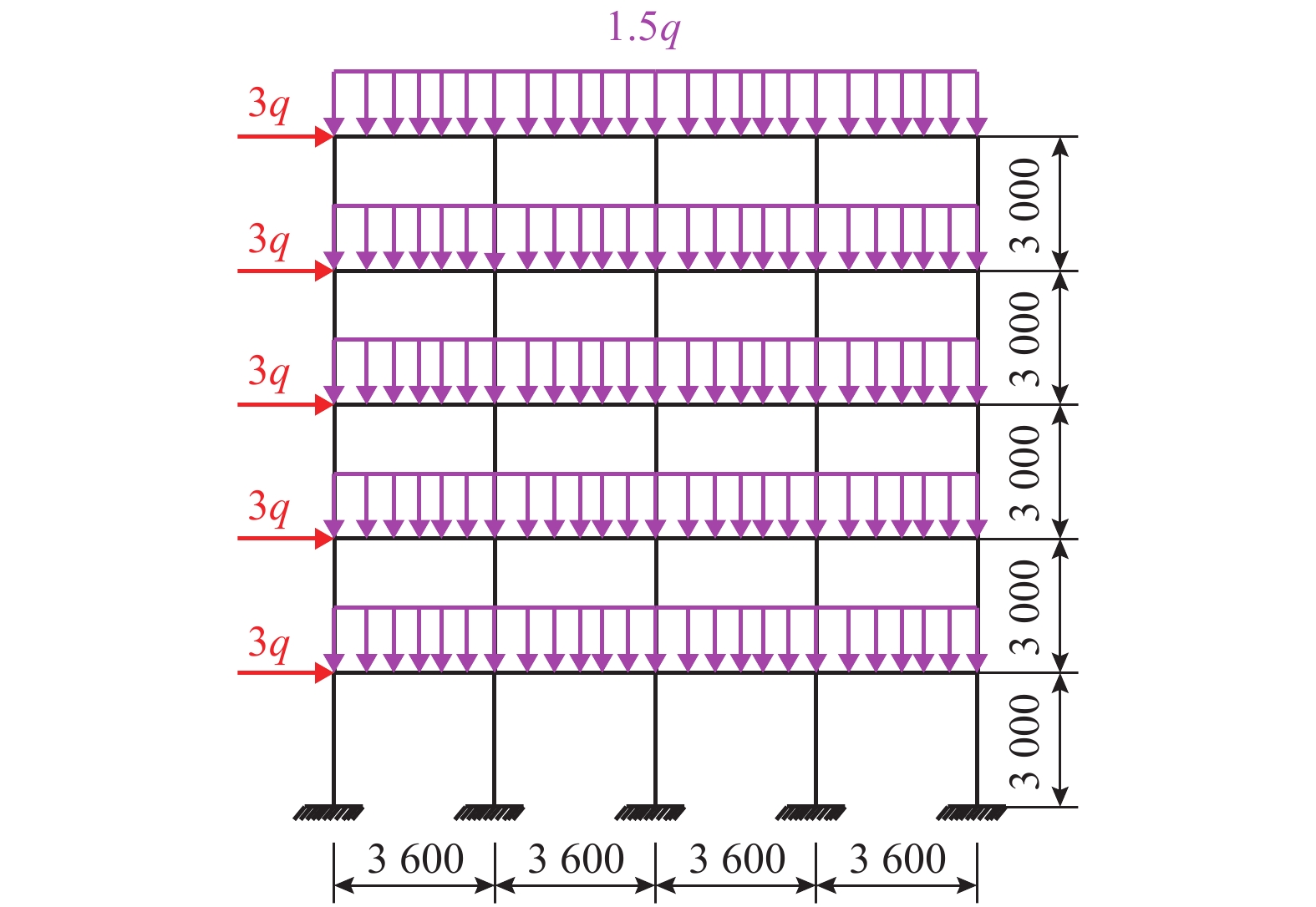
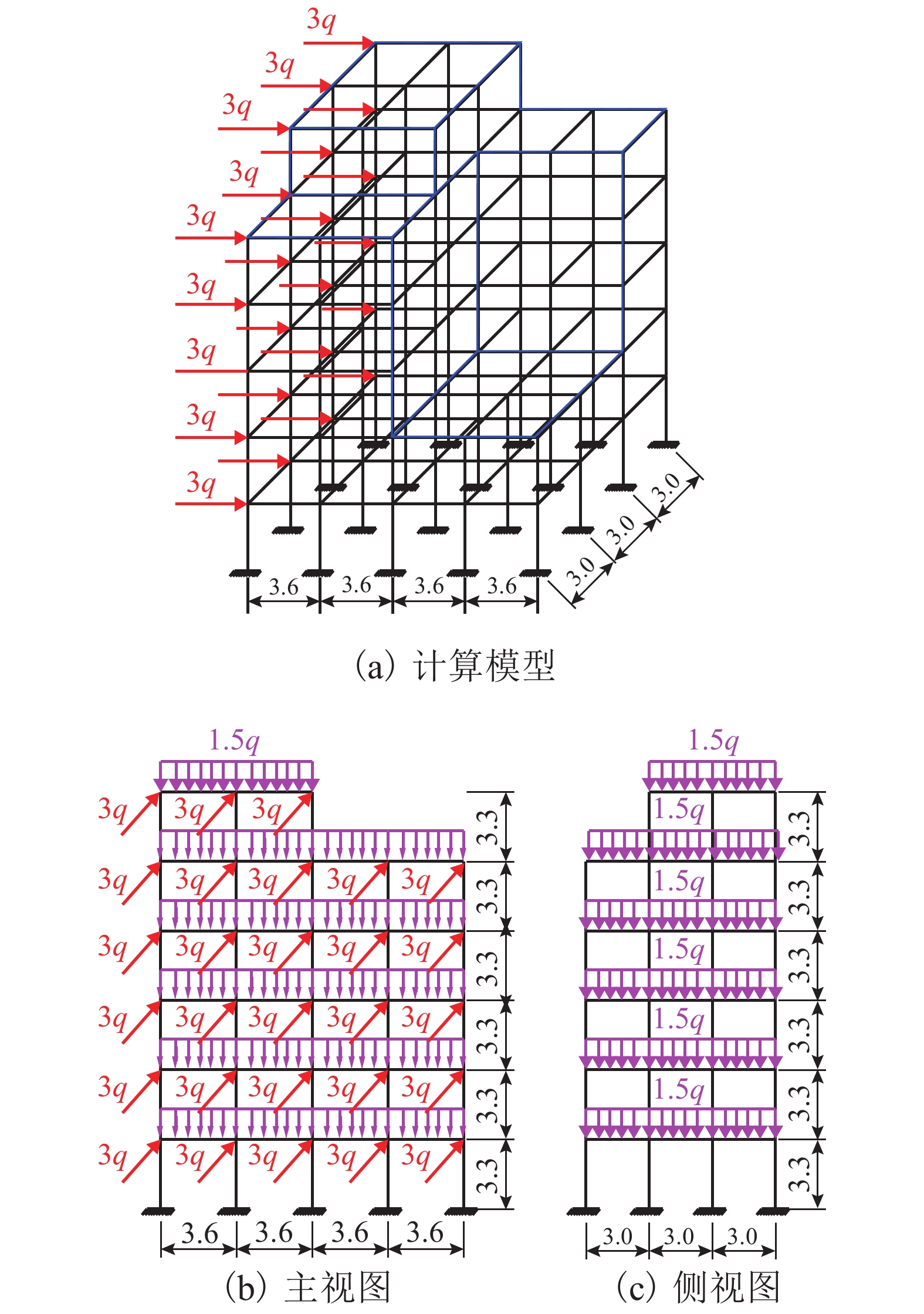
Table 7. Geometry parameters
m 构件 b h t1 t2 梁 0.1 0.15 0.025 0.015 柱 0.2 0.30 0.050 0.030
下载: 导出CSV
表 8 内力组合对结构极限承载力的影响
Table 8. Influence of internal force combination on ultimate bearing capacity
参数 EPIA EMRM HGYF[17] 本文HGYF 极限荷载/（kN•m−1） 28.94 151.37 27.85 计算时间/s 554.2 2.6 50.9 相对误差/% 423.05 3.77
下载: 导出CSV
表 9 荷载初值对结构极限承载力的影响
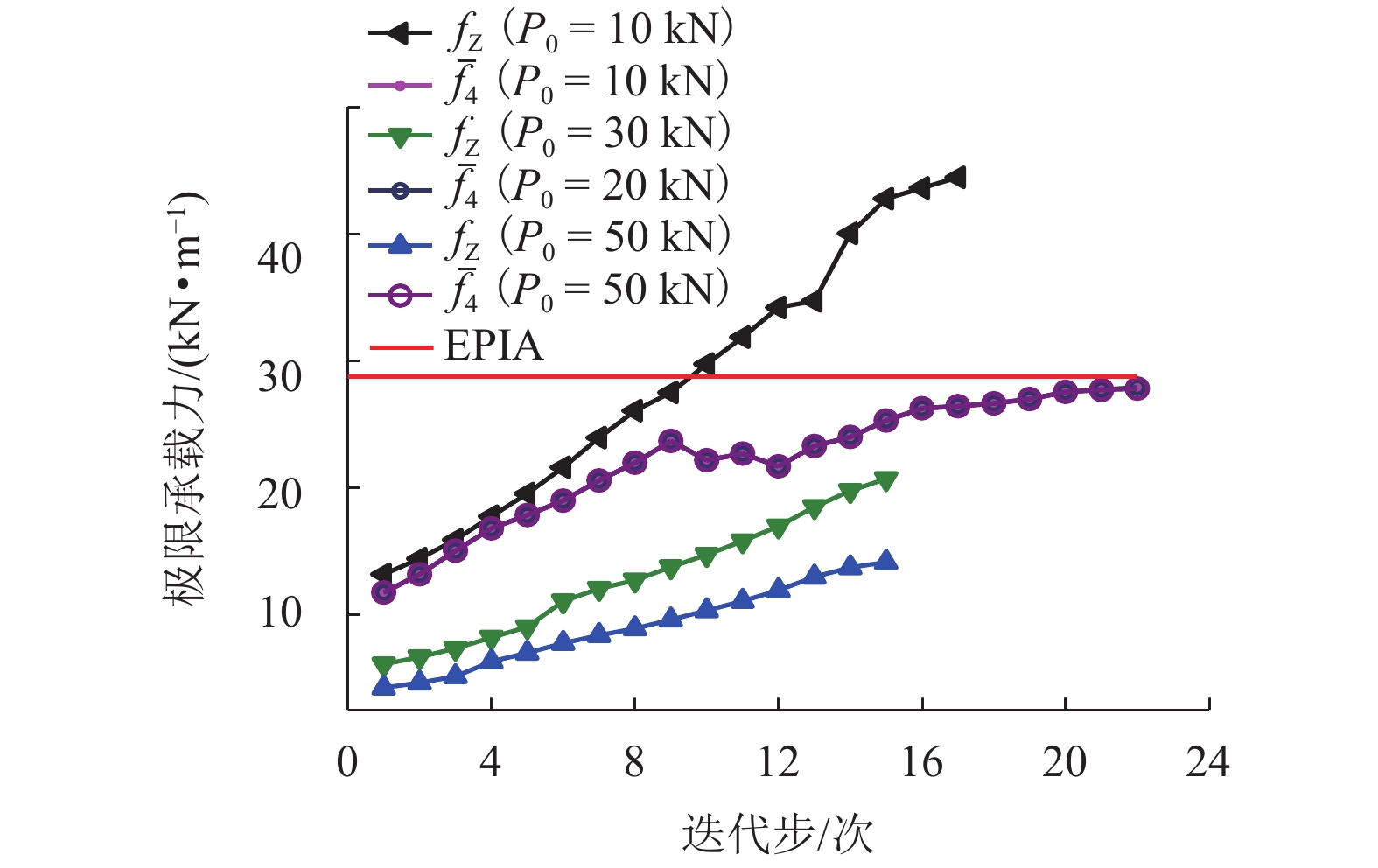
Table 9. Influence of the initial load on ultimate bearing capacity
计算方法 文献来源 荷载初值/（kN•m−1） 极限荷载/（kN•m−1） 计算时间/s 相对误差/% EPIA 50 28.94 554.2 EMRM GYF[8] 10 44.44 30.2 53.56 30 20.68 27.7 28.54 50 14.11 28.8 51.24 GYF[9] 10 42.87 31.3 48.12 30 19.63 32.9 32.17 50 12.39 32.9 57.19 GYF[10] 10 34.66 37.3 19.77 30 19.17 36.1 33.76 50 11.26 35.2 61.09 本文HGYF 10 27.85 50.9 3.77 30 27.85 50.8 3.77 50 27.85 50.9 3.77
下载: 导出CSV
表 10
$\beta $ 和$\gamma $ 对结果的影响Table 10. Influence of
$\beta $ and$\gamma $ on the results计算方法 $\beta $ $\gamma $ 极限荷载/
（kN•m−1）相对误差/% EPIA 1.0 5 16.95 10 10.53 1.5 5 34.26 10 21.21 2.0 5 60.62 10 37.69 EMRM 1.0 5 16.73 1.30 10 10.40 1.23 1.5 5 33.49 2.25 10 20.74 2.24 2.0 5 59.27 2.23 10 36.87 2.18
下载: 导出CSV
-
YUAN Huanxin, WANG Yuanqing, GARDNER L, et al. Local-overall interactive buckling of welded stainless steel box section compression members[J]. Engineering Structures, 2014, 67(4): 62-76. SHEN Jiajia, WADEE M A. Length effects on interactive buckling in thin-walled rectangular hollow section struts[J]. Thin-Walled Structures, 2017, 128(S1): 152-170. SCHILLO N, FELDMANN M. Interaction of local and global buckling of box sections made of high strength steel[J]. Thin-Walled Structures, 2017, 128(S1): 126-140. 管民生, 黄献奇, 杜宏彪, 张金刚. 矩形钢管高强混凝土框架抗震性能分析[J]. 西南交通大学学报, 2019, 54(3): 483-491.GUAN Minsheng, HUANG Xianqi, DU Hongbiao, et al. Seismic behavior of rectangular high-strength concrete-filled steel tube frame structure[J]. Journal of Southwest Jiaotong University, 2019, 54(3): 483-491. 申红侠,刘翔. 高强钢焊接方形截面偏压构件整体和局部相关屈曲承载力分析[J]. 建筑结构,2014,44(4): 35-38.SHEN Hongxia, LIU Xiang. Analysis on the ultimate carrying capacities of local-overall interaction of high-strength steel welded square-box section columns loaded with eccentricity[J]. Building Structure, 2014, 44(4): 35-38. 李国强,闫晓雷,陈素文. Q460高强钢焊接箱形压弯构件极限承载力试验研究[J]. 土木工程学报,2012,45(8): 67-73.LI Guoqiang, YAN Xiaolei, CHEN Suwen. Experimental study on the ultimate bearing capacity of welded box-section columns using Q460 high strength steel in bending and axial compression[J]. Journal of Civil Engineering, 2012, 45(8): 67-73. 邵永波, 朱红梅, 杨冬平. 轴压作用下CFRP加固圆钢管短柱的静力承载力分析[J]. 西南交通大学学报, 2020, 55(1): 167-174.SHAO Yongbo, ZHU Hongmei, YANG Dongping. Static bearing capacity analysis of CFRP-reinforced short CHS steel tubular columns under axial compression[J]. Journal of Southwest Jiaotong University, 2020, 55(1): 167-174. ZHOU Suiping, CHEN Huifa. Design criteria for box columns under biaxial loading[J]. Journal of Structural Engineering, 1985, 111(12): 2643-2658. doi: 10.1061/(ASCE)0733-9445(1985)111:12(2643) DUAN Lian, CHEN Huifa. A yield surface equation for doubly symmetrical sections[J]. Engineering Structures, 1990, 12(2): 114-119. doi: 10.1016/0141-0296(90)90016-L CEN. Eurocode3: design of steel structures: EN1993-1-1[S]. Brussels: [s.n.], 1993. MACKENZIE D, BOYLE J T. Elastic compensation method for limit and shakedown analysis:a review[J]. Journal of Strain Analysis for Engineering Design, 2005, 35(3): 171-188. MAHMOOD S L, SESHADRI R. Limit load evaluation using the m α-Tangent multiplier in conjunction with elastic modulus adjustment procedure[J]. Journal of Pressure Vessel Technology, 2013, 135(5): 051203.1-051203.9. doi: 10.1115/1.4024452 杨绿峰,余波,张伟. 弹性模量缩减法分析杆系和板壳结构的极限承载力[J]. 工程力学,2009,26(12): 64-70.YANG Lufeng, YU Bo, ZHANG Wei. The elastic modulus reduction method for load carring capacity evaluation of frame,plate and shell structures[J]. Engineering Mechanics, 2009, 26(12): 64-70. CHEN Xiahui, GAO Bingjun, WANG Xingang. Evaluation of limit load analysis for pressure vessels—part Ⅱ Robust methods[J]. Steel & Composite Structures, 2017, 23(1): 131-142. YANG Lufeng, LI Qi, ZHANG Wei, et al. Homogeneous generalized yield criterion based elastic modulus reduction method for limit analysis of thin-walled structures with angle steel[J]. Thin-Walled Structures, 2014, 80(9): 153-158. YANG Lufeng, YU Bo, ZHU Jianwen. Incorporated strength capacity technique for limit load evaluation of trusses and framed structures under constant loading[J]. Journal of Structural Engineering, 2015, 141(11): 04015023.1-15023.11. doi: 10.1061/(ASCE)ST.1943-541X.0001252 欧伟,张伟,冯瑛琪,等. 箱型截面的齐次广义屈服函数与结构极限承载力[J]. 华南理工大学学报(自然科学版),2014,42(6): 96-101.OU Wei, ZHANG Wei, FENG Yingqi, et al. Homogeneous generalized yield function and ultimate bearing capacity of structures with box section[J]. Journal of South China University of Technology (Natural Science Edition), 2014, 42(6): 96-101. 徐秉业. 结构塑性极限分析[M]. 北京: 中国建筑工业出版社, 1985: 62-67. BARRERA O, COCKS A C F, PONTER A R S. The linear matching method applied to composite materials:a micromechanical approach[J]. Composites Science & Technology, 2011, 71(6): 797-804. -
下载:
点击查看大图
计量
- 文章访问数: 629
- HTML全文浏览量: 319
- PDF下载量: 18
- 被引次数: 0