Random Walking Crowd Model Considering Pedestrian Synchronization Rate
-
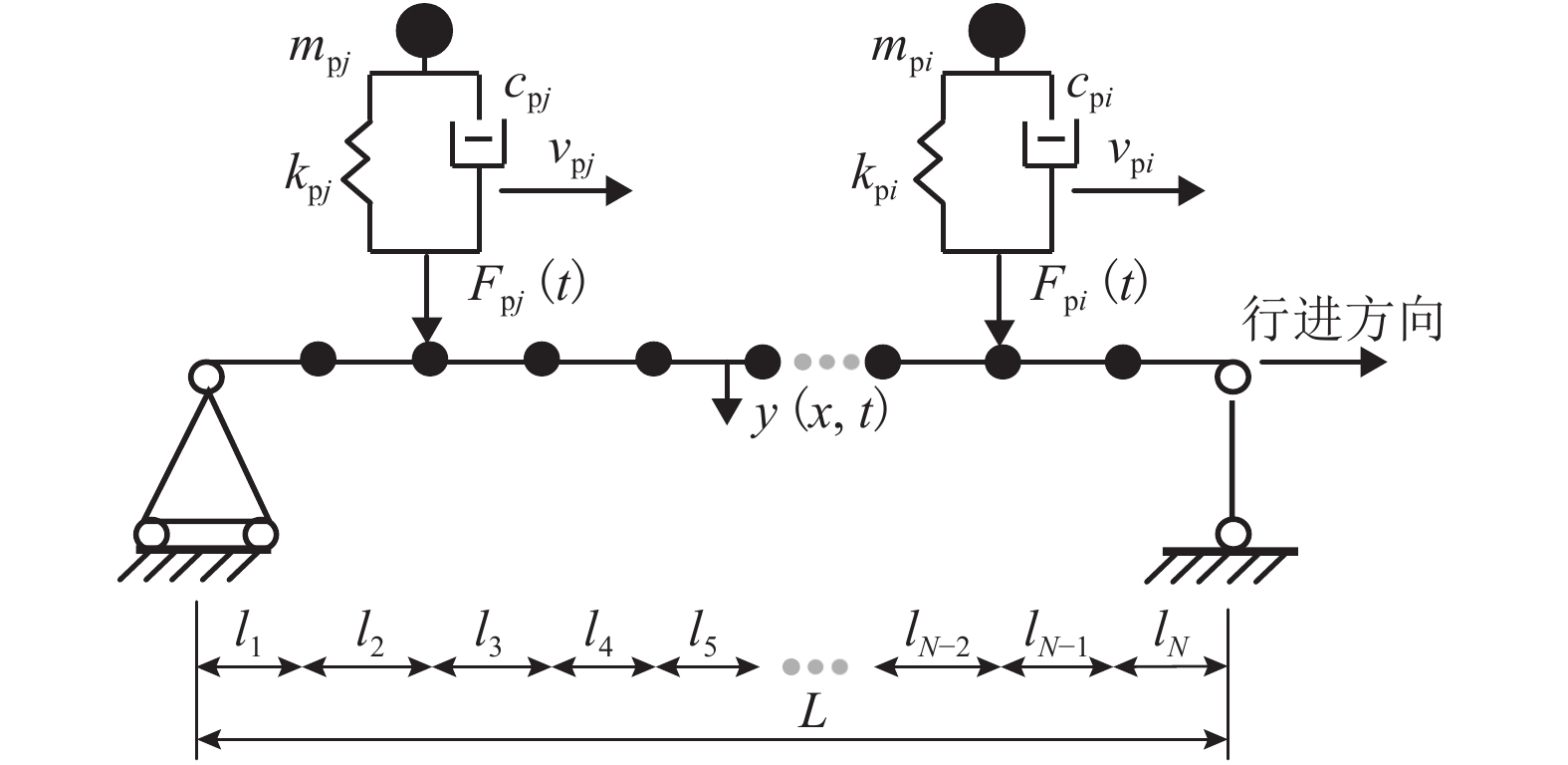
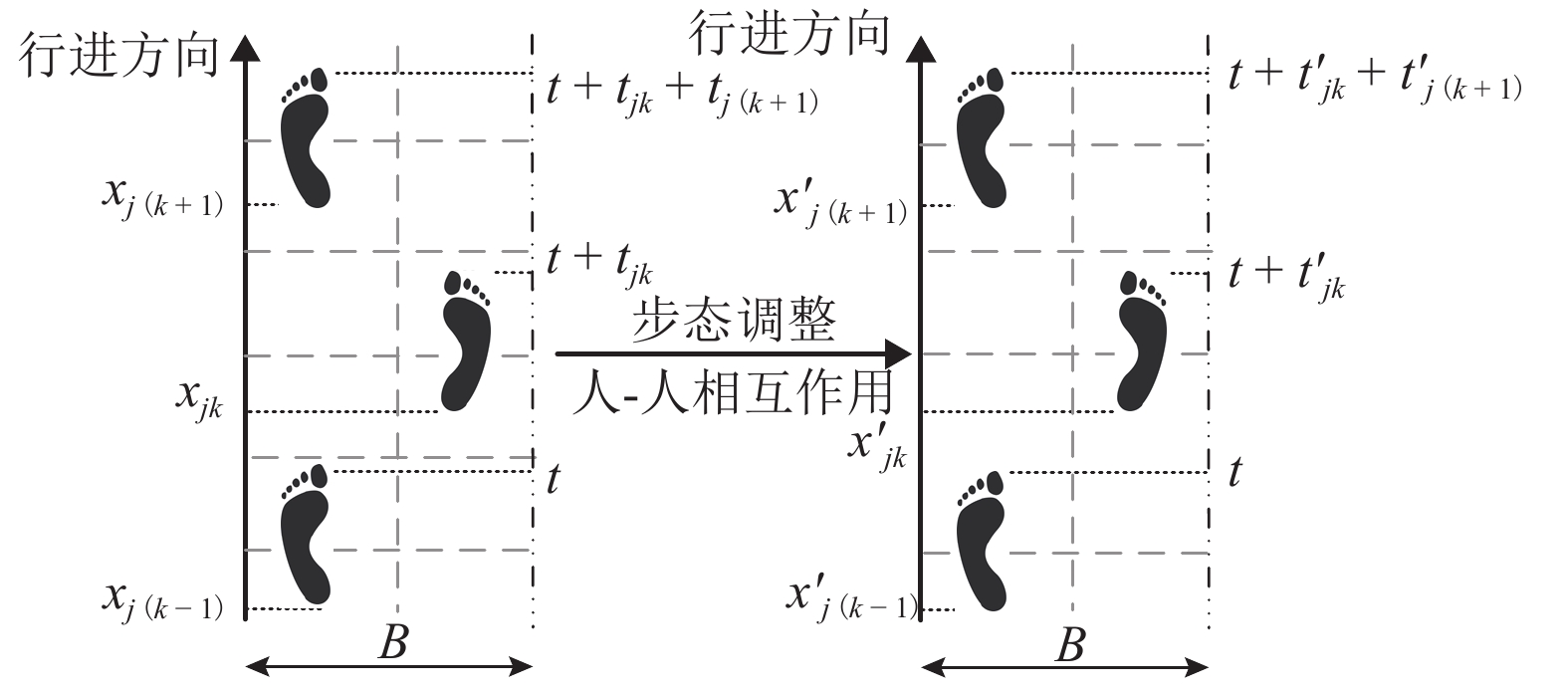
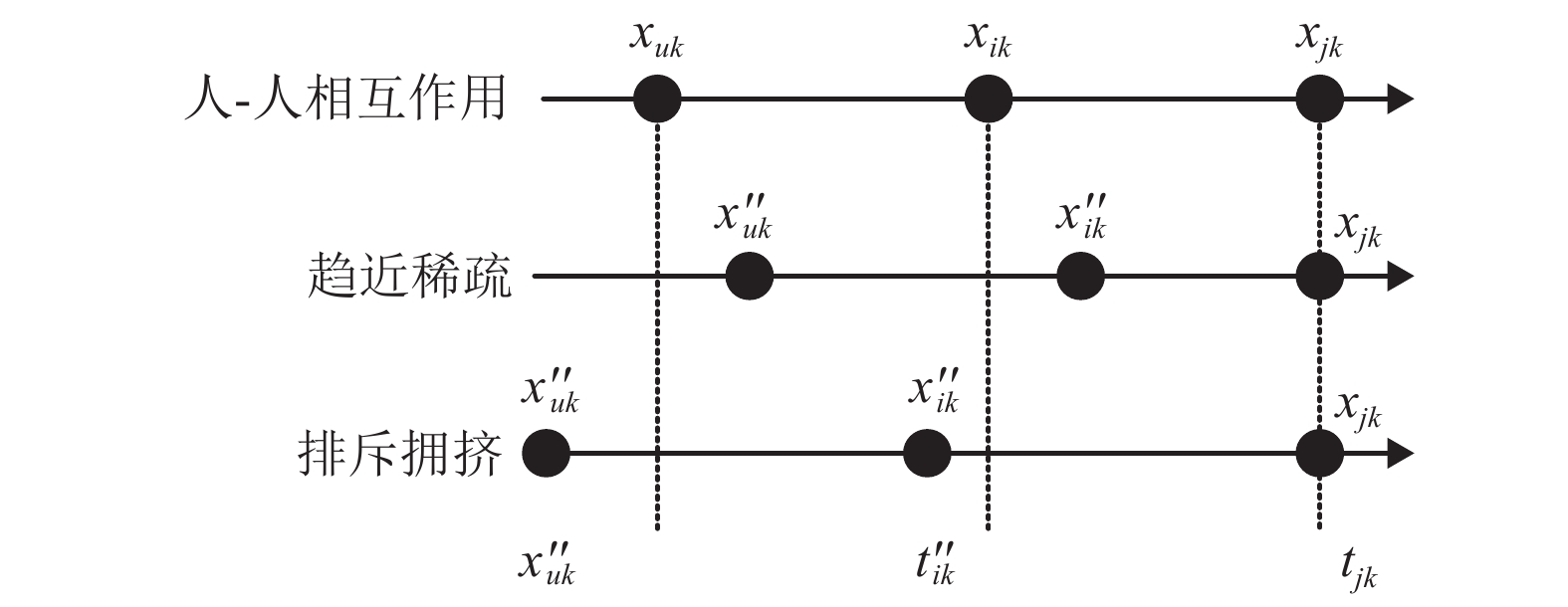
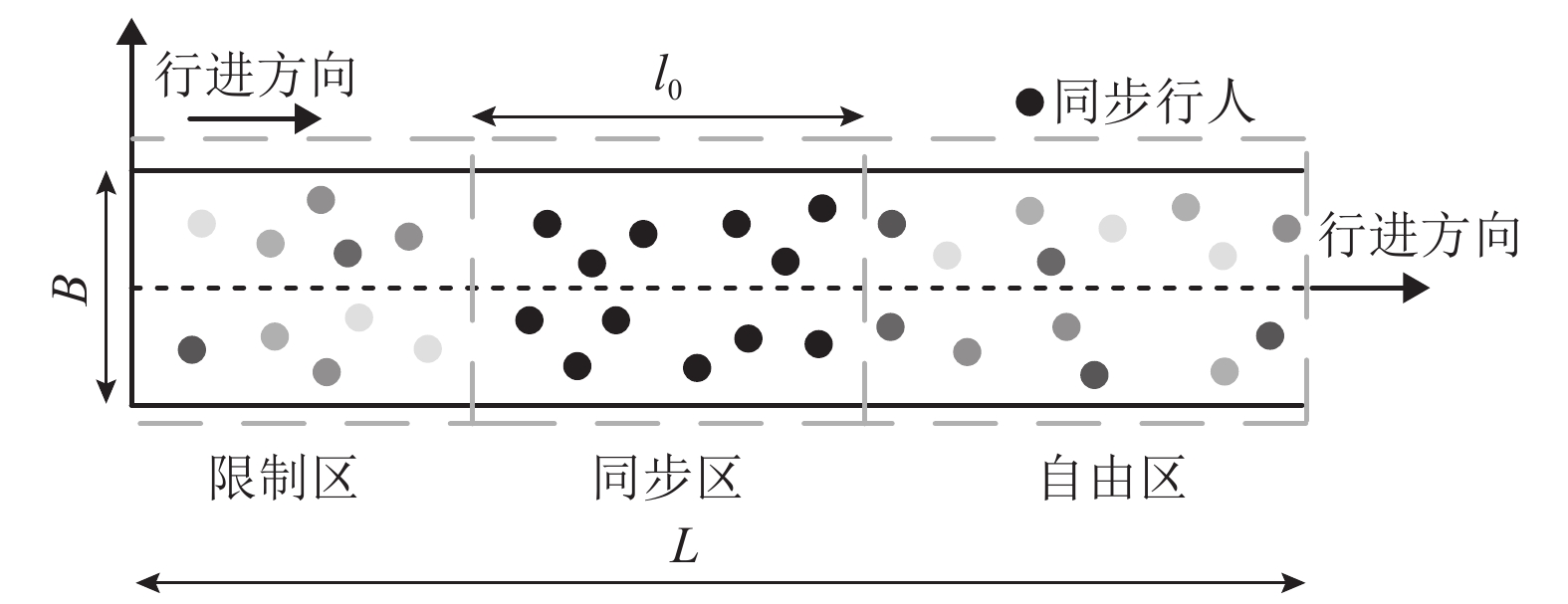
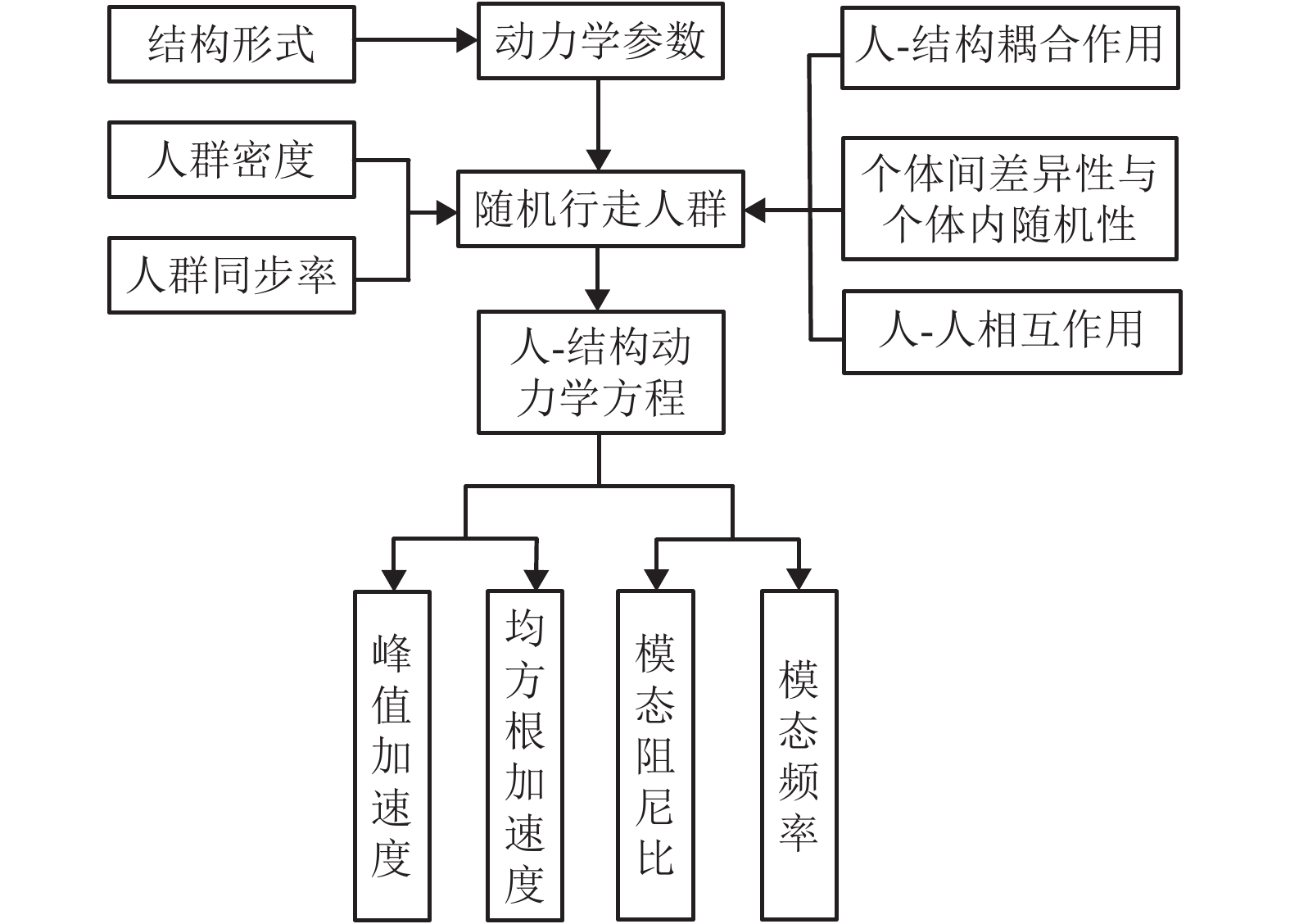
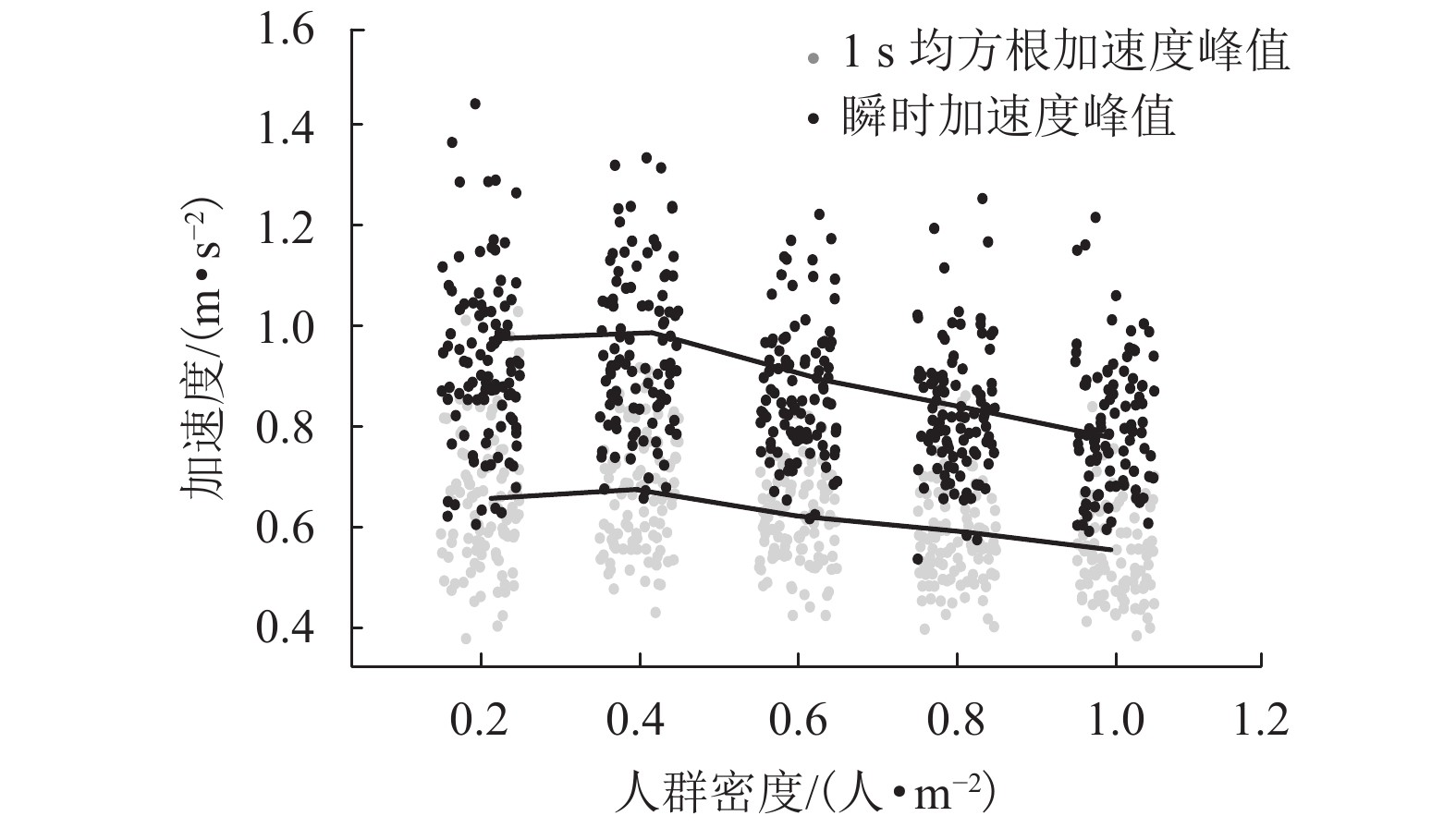
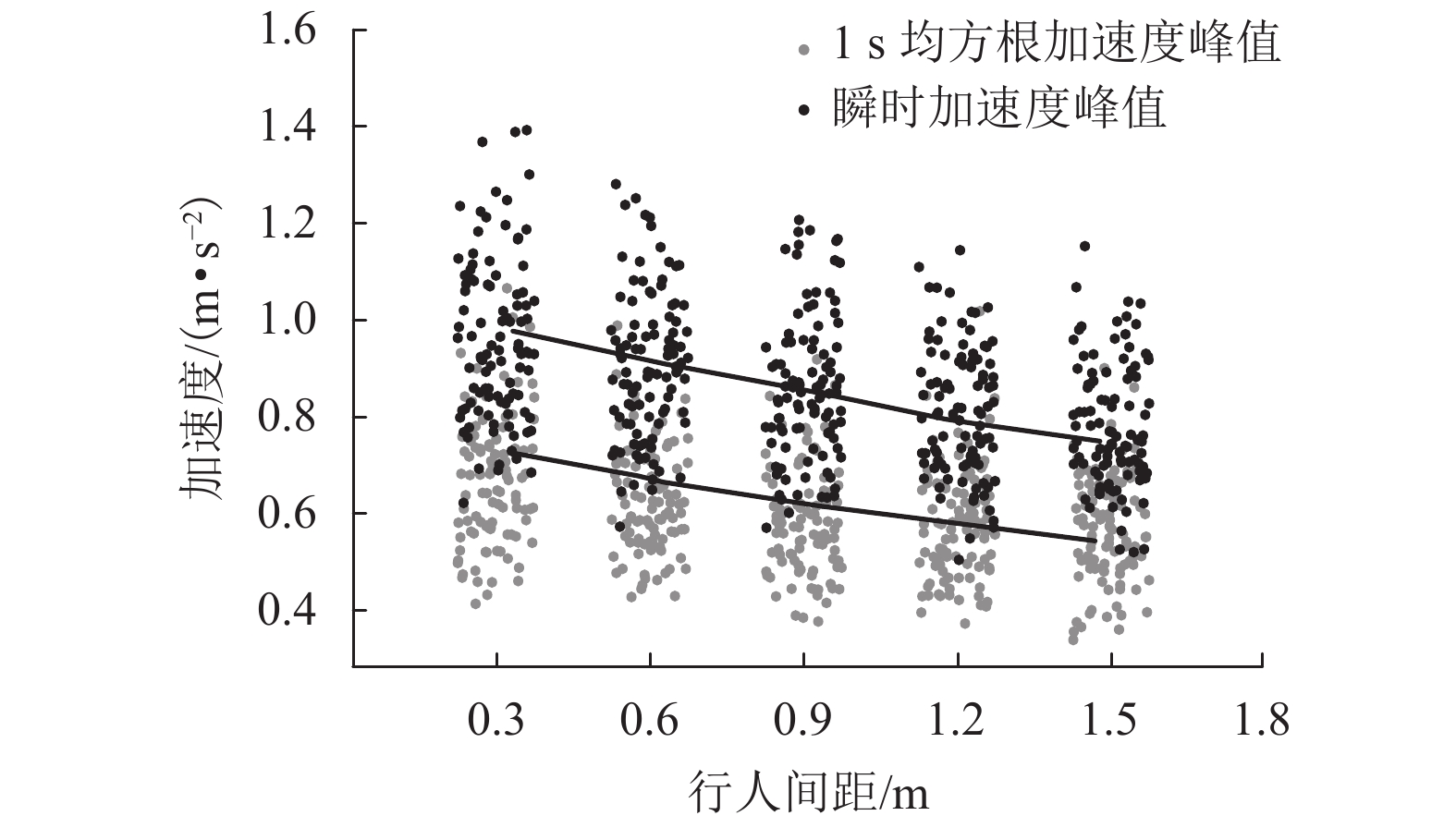
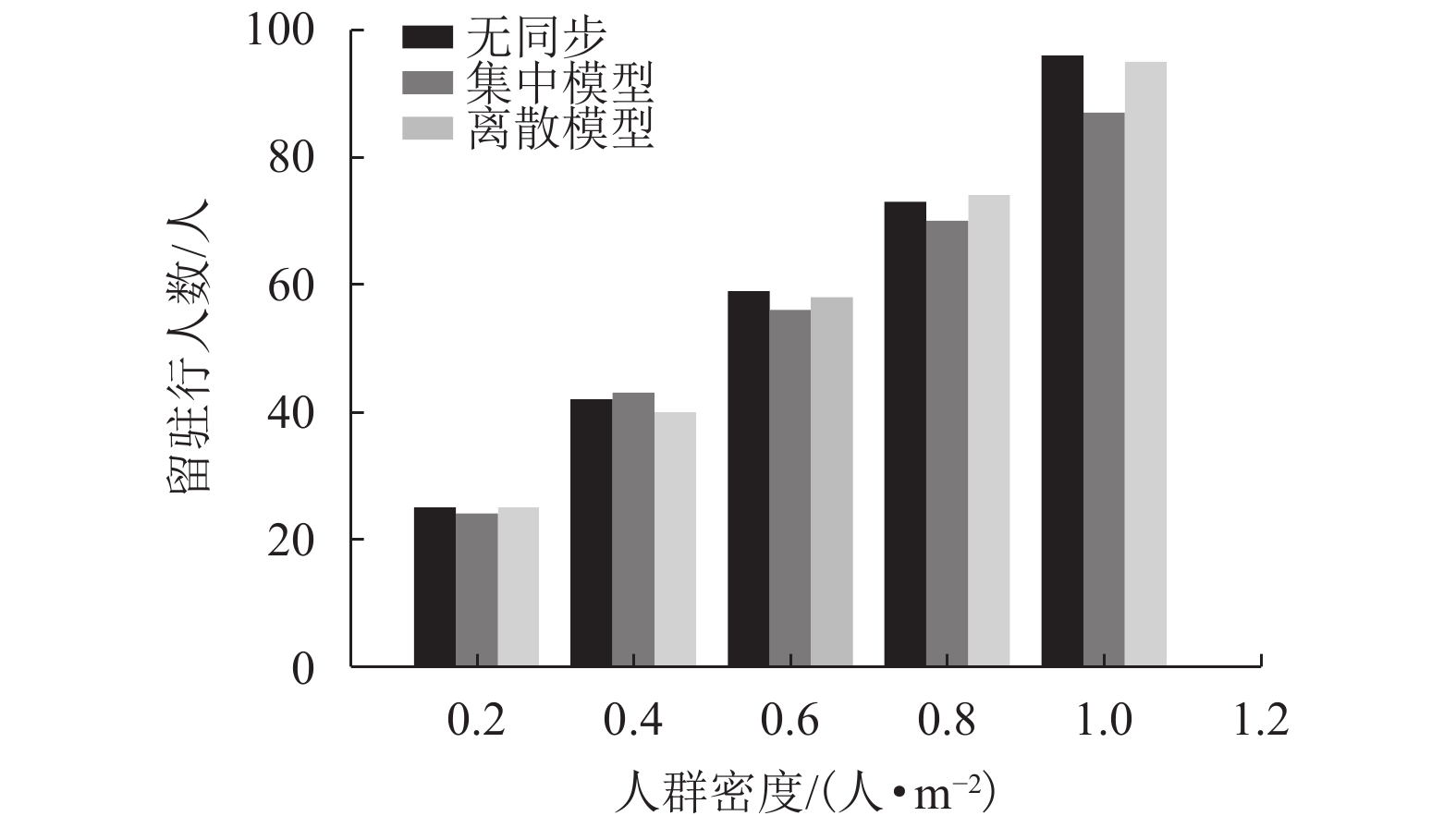
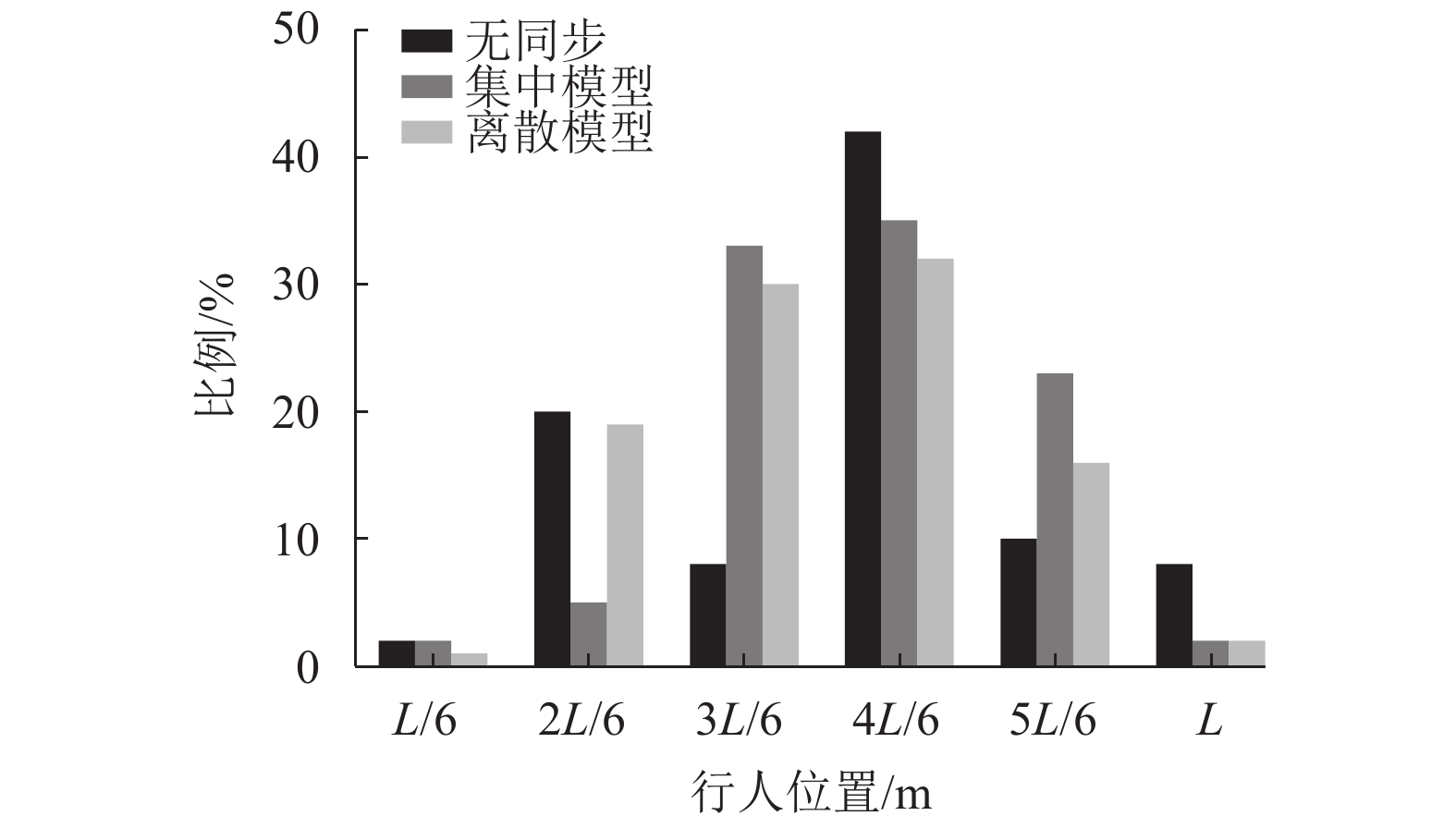
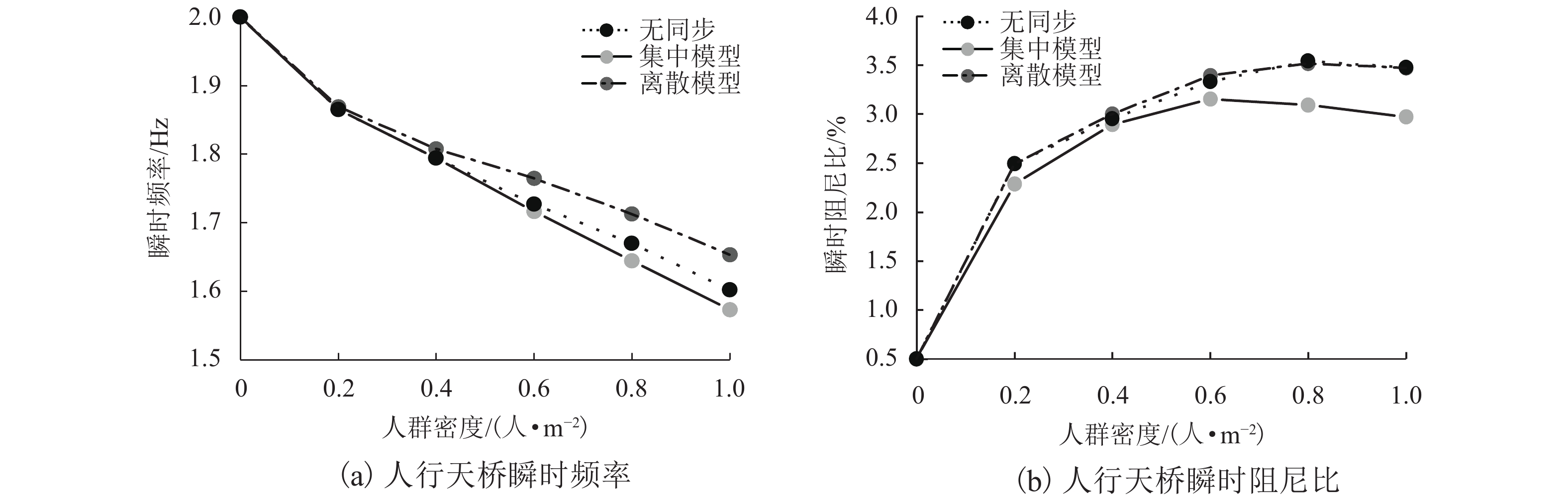
摘要: 为了研究行走人群协同性对结构人致振动的影响，基于考虑行人同步率的随机行走人群模型，对人群行走下人行天桥的竖向振动问题就行了分析. 首先通过行走人群随机性分析，提出了考虑行人同步率的随机行走人群集中模型和离散模型；其次在两类模型下考虑人-结构竖向耦合作用，建立了随机行走人群作用下结构竖向振动响应分析方法；最后对比分析了人行天桥在不同随机行走人群模型下的竖向加速度响应和动力特性参数的变化规律. 研究结果表明：两类模型行人行走下，人行天桥的1 s均方根加速度响应随人群密度的提高先增大后减小；人群密度超过0.2人/m2后，随机行走人群离散模型下的人行天桥1 s均方根加速度大于集中模型，且增大集中模型同步区行人间距有利于减小结构振动响应；随着人群密度的增大，人行天桥瞬时频率不断减小，瞬时阻尼比则先增大后减小，集中模型和离散模型下人行天桥瞬时阻尼比分别最大提高到6倍和7倍；考虑行人同步率的随机行走人群模型能准确反映人行天桥实际所受到的人群行走荷载作用，可为人行天桥人致振动响应分析与评估提供参考.
-
关键词:
- 人-结构竖向耦合作用 /
- 人致振动 /
- 随机人群 /
- 振动分析 /
- 同步率
Abstract: In order to study the influence of walking crowd synergy on the human-induced vibration of structures, the vertical vibration of a footbridge under the action of walking crowd was analyzed using the random walking crowd model considering pedestrian synchronization rate. Firstly, a random walking crowd centralized model and discrete model considering pedestrian synchronization rate were proposed by random analysis of the walking crowd. Secondly, a method for vertical vibration response analysis of structure subjected to random walking crowd was established by considering the vertical coupling effect between human and structure under the two models. Finally, change rules of vertical acceleration responses and dynamic characteristic parameters of the footbridge under the two different random walking crowd models were compared and analyzed. Results show that the 1-s root-mean-square (RMS) acceleration responses of the footbridge under the two pedestrian walking models both increase first and then decrease with the crowd density increasing. Beyond the crowd density of 0.2 person/m2, the 1-s RMS acceleration of the footbridge in the random walking crowd discrete model is greater than that in the centralized model, and increasing the pedestrian spacing in the synchronization zone of the centralized model is beneficial to reducing structural vibration responses. As crowd density increases, the instantaneous frequency of footbridge decreases constantly; the instantaneous damping ratio of the footbridge increases first and then decreases, with a maximum 6-fold and 7-fold increase under the centralized model and the discrete model, respectively. In short, the random walking crowd model considering pedestrian synchronization rate can accurately reflect the actual crowd walking load of footbridges and therefore provide reference for the analysis and evaluation of human-induced vibration responses of footbridges. -
图 6 随机行走人群建模及结构振动响应分析流程
Figure 6. Flow diagram of random walking crowd modeling and structural vibration response analysis
图 7 不同人群密度下人行天桥竖向加速度响应
Figure 7. Vertical acceleration response of footbridge under different crowd density
图 8 不同人群密度下人行天桥竖向峰值加速度
Figure 8. Vertical acceleration peak of footbridge under different crowd density
表 1 不同人群密度下1 s均方根加速度均值及变异系数
Table 1. Mean square root acceleration and variation coefficient
人群密度/（人•m−2） 加速度均值/（m•s−2） 变异系数/% 集中模型 离散模型 无同步模型 集中模型 离散模型 无同步模型 0.2 0.643 0.631 0.627 20.3 17.3 16.7 0.4 0.661 0.688 0.675 16.8 15.6 17.6 0.6 0.609 0.725 0.709 14.6 16.3 15.9 0.8 0.576 0.699 0.672 16.2 17.5 14.2 1.0 0.542 0.654 0.645 16.0 14.9 16.2 
下载: 导出CSV
-
马斐,张志强,张晓峰,等. 高铁站房大跨钢楼盖行车和人群荷载激励下振动响应实测与分析[J]. 建筑结构学报,2018,39(1): 109-119.MA Fei, ZHANG Zhiqiang, ZHANG Xiaofeng, et al. Vibration response measurement and analysis of large-span steel floor structure at high-speed rail station under moving train and crowd excitation[J]. Journal of Building Structures, 2018, 39(1): 109-119. ZHANG S, XU L, QIN J. Vibration of lightweight steel floor systems with occupants:modelling,formulation and dynamic properties[J]. Engineering Structures, 2017, 147: 652-665. doi: 10.1016/j.engstruct.2017.06.008 谢伟平,冯金鹏,何卫. 基于自激励人体模型的人-结构竖向相互作用研究[J]. 振动与冲击,2017,36(21): 28-33.XIE Weiping, FENG Jinpeng, HE Wei. Vertical human-structure interaction based on a self-exciting human model[J]. Journal of Vibration and Shock, 2017, 36(21): 28-33. 操礼林,曹栋,于国军. 人-结构竖向相互作用两类简化模型分析[J]. 西南交通大学学报,2018,53(6): 1166-1172. doi: 10.3969/j.issn.0258-2724.2012.06.003CAO Lilin, CAO Dong, YU Guojun. Two simplified models for human-structure vertical interaction[J]. Journal of Southwest Jiaotong University, 2018, 53(6): 1166-1172. doi: 10.3969/j.issn.0258-2724.2012.06.003 VAN NIMMEN K, LOMBAERT G, DE ROECK G, et al. Vibration serviceability of footbridges:evalua-tion of the current codes of practice[J]. Engineering Structures, 2014, 59: 448-461. doi: 10.1016/j.engstruct.2013.11.006 RACIC V, PAVIC A, BROWNJOHN J M W. Experimental identification and analytical modelling of human walking forces:literature review[J]. Journal of Sound and Vibration, 2009, 326(1): 1-49. VENUTI F, RACIC V, CORBETTA A. Modelling framework for dynamic interaction between multiple pedestrians and vertical vibrations of footbridges[J]. Journal of Sound and Vibration, 2016, 379: 245-263. doi: 10.1016/j.jsv.2016.05.047 KASPERSKI M. Realistic simulation of a random pedestrian flow[J]. Procedia Engineering, 2017, 199: 2814-2819. doi: 10.1016/j.proeng.2017.09.341 罗鹏. 大跨楼盖结构人群荷载模拟及振动响应分析[D]. 南京: 东南大学土木工程学院, 2015. 朱前坤,刘路路,杜永峰,等. 考虑行人-结构相互作用的悬挑钢筋桁架楼承板振动控制研究[J]. 建筑结构学报,2018,39(1): 99-108.ZHU Qiankun, LIU Lulu, DU Yongfeng, et al. Human-induced vibration and control for cantilever steel bartruss deck slab based on pedestrain-structure interaction[J]. Journal of Building Structures, 2018, 39(1): 99-108. 陈隽. 人致荷载研究综述[J]. 振动与冲击,2017,36(23): 1-9.CHEN Jun. A review of human- induced loads study[J]. Journal of Vibration and Shock, 2017, 36(23): 1-9. VENUTI F, BRUNO L. An interpretative model of the pedestrian fundamental relation[J]. Comptes Rendus Mécanique, 2007, 335(4): 194-200. doi: 10.1016/j.crme.2007.03.008 操礼林. 高铁候车厅大跨楼盖人致振动响应分析与减振控制研究[D]. 南京: 东南大学, 2016. CAPRANI C C, KEOGH J, ARCHBOLD P, et al. Enhancement factors for the vertical response of footbridges subjected to stochastic crowd loading[J]. Computers & Structures, 2012, 102/103(1): 87-96. 杨予,杨云芳,洪震,等. 人体站姿竖向振动等效单自由度模型参数研究[J]. 振动与冲击,2012,31(23): 154-157. doi: 10.3969/j.issn.1000-3835.2012.23.029YANG Yu, YANG Yunfang, HONG Zhen, et al. Parameters of an equivalent SDOF vertical model for a standing human body[J]. Journal of Vibration and Shock, 2012, 31(23): 154-157. doi: 10.3969/j.issn.1000-3835.2012.23.029 -
下载:
点击查看大图
图(15) / 表(1)
计量
- 文章访问数: 631
- HTML全文浏览量: 288
- PDF下载量: 20
- 被引次数: 0