Passenger Flow Prediction for Guangzhou-Zhuhai Intercity Railway Based on SARIMA Model
-
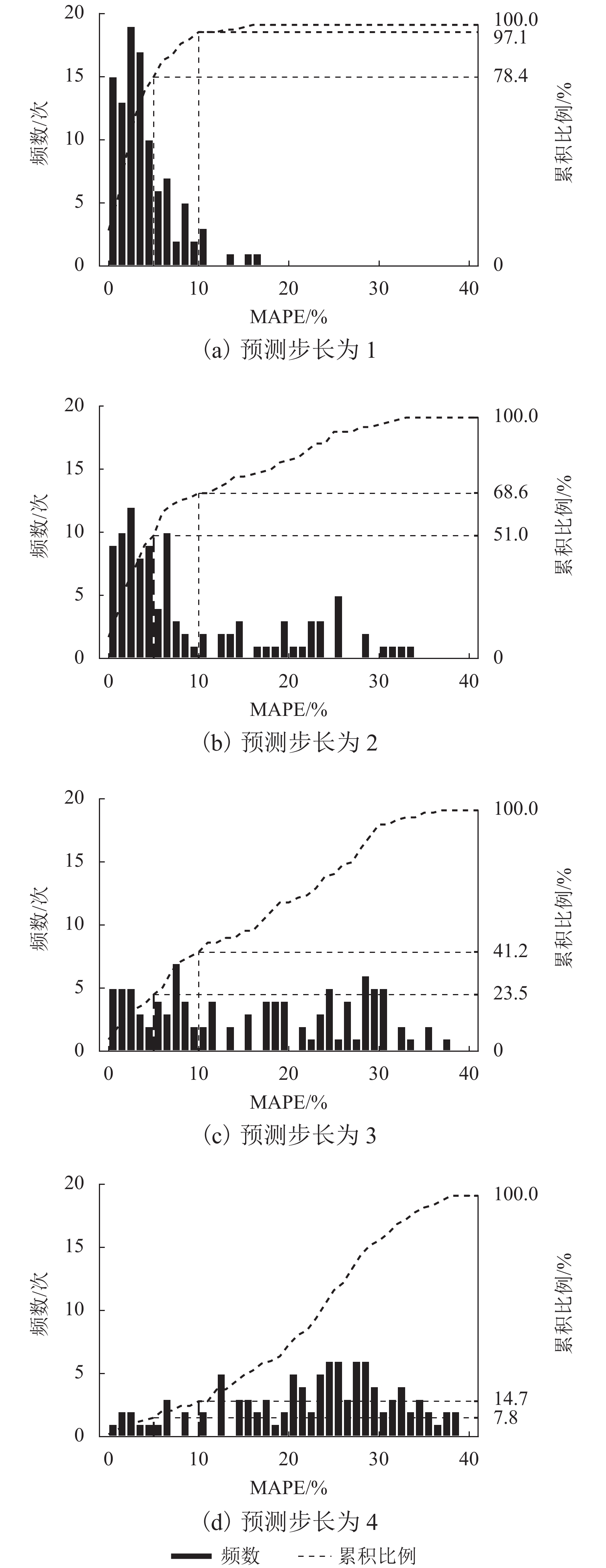
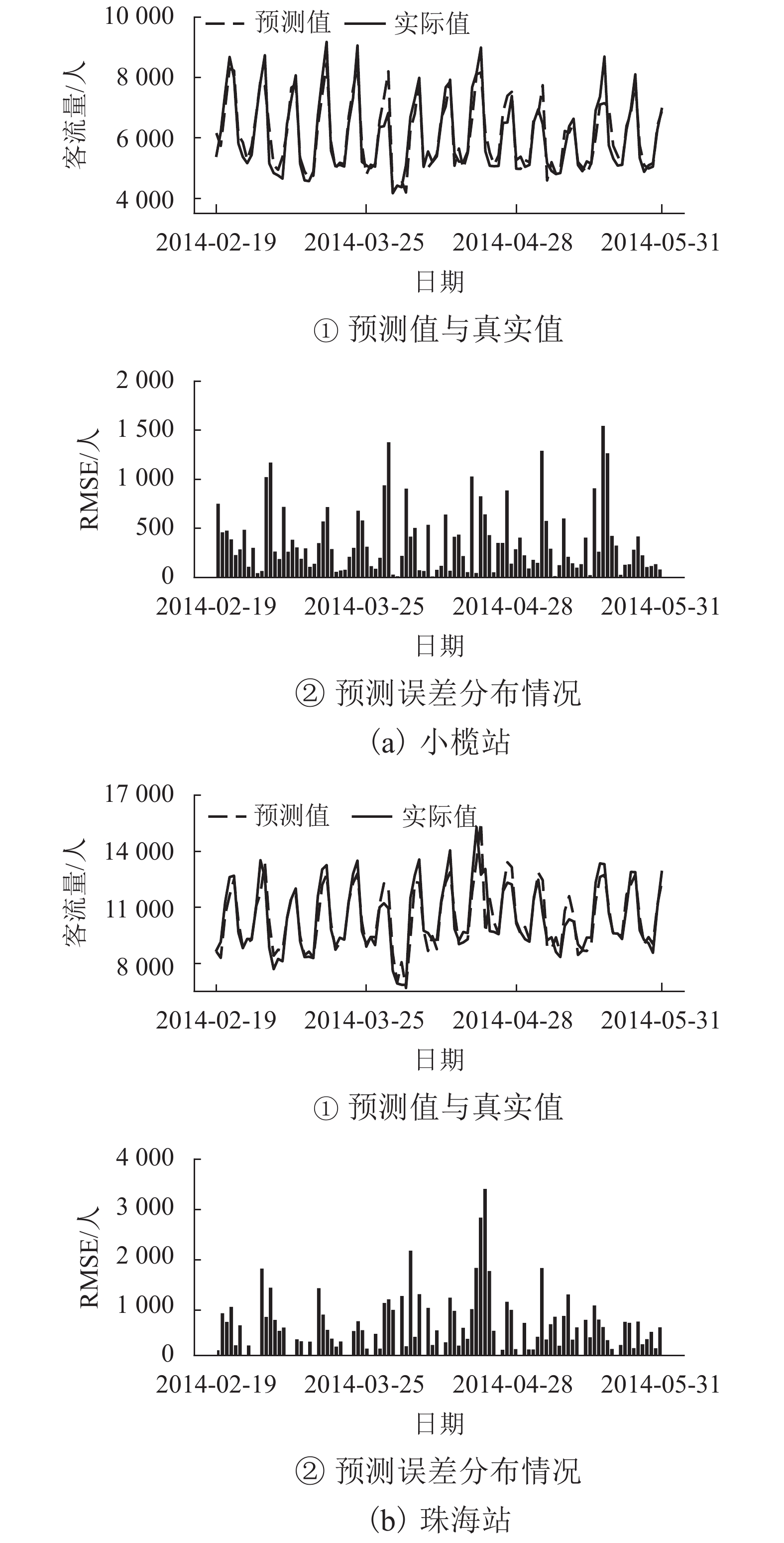
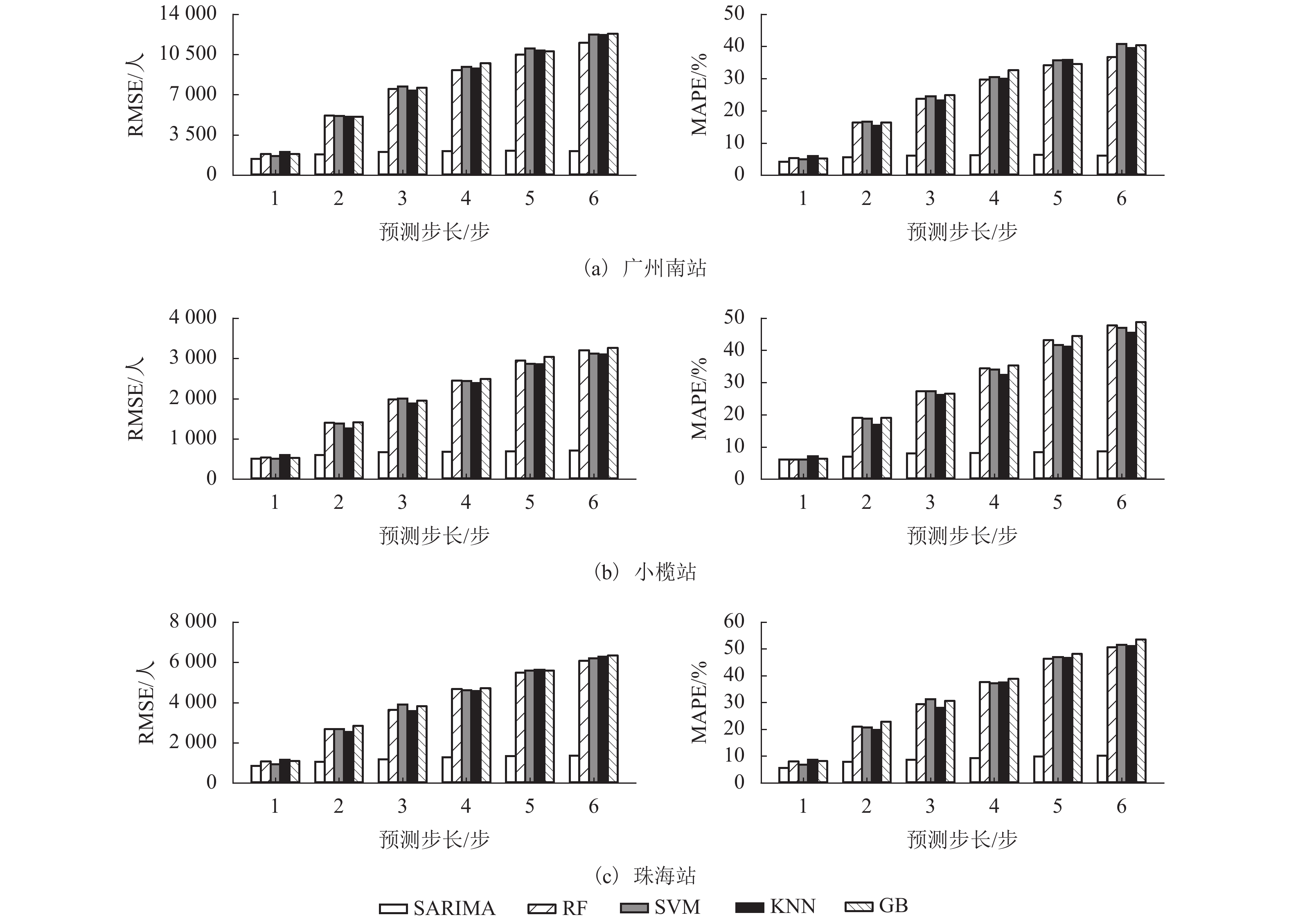
摘要: 为实现铁路车站发送客流量的短期预测，研究预测步长对短期客流预测效果的影响，分析了广珠城际铁路车站发送客流的特征和变化规律，结合客流特征及季节性差分自回归滑动平均模型（seasonal autoregressive integrated moving average，SARIMA）的适用性，构建了SARIMA客流预测模型，利用Python软件中的Statsmodels模块完成了SARIMA客流模型的精细化调参，以广州南站、小榄站的发送客流量为例验证了模型的有效性. 结果表明，SARIMA预测模型可以较好地适用于不同数量等级的客流预测，其预测精度随预测步长的增加而降低. 预测步长为1时，广州南站、小榄站、珠海站客流预测平均绝对百分比误差（mean absolute percentage error，MAPE）值分别为3.97%，5.83%，5.43%；预测步长增加为2时，各车站客流预测误差显著增加，广州南站、小榄站、珠海站客流预测误差MAPE值分别为5.31%，6.79%，7.62%；预测步长大于2时，预测误差基本保持稳定. 将SARIMA模型预测效果与随机森林（random forest， RF）、支持向量机（support vector machine， SVM）、梯度提升算法（gradient boosting， GB）、K最近邻算法（K-nearest neighbor， KNN）模型或方法的预测效果进行对比，预测步长为1时，SARIMA模型预测效果略优于其余4种模型，5种预测模型预测精度差距较小；预测步长大于1时，RF、SVM、GB、KNN模型预测误差随预测步长显著增加，预测误差为SARIMA模型的数倍. SARIMA模型在客流时间序列的多步预测方面具有较大的优势.Abstract: To achieve the short-term prediction on the railway passenger flow and analyze the influence of prediction step on prediction accuracy, firstly, the characteristics and variation of passenger flow for Guangzhou-Zhuhai intercity railway were analyzed. Then, considering the passenger flow characteristics, a prediction model based on the seasonal autoregressive integrated moving average (SARIMA) was built with the Statsmodels module in Python. Next, the model performance was validated on different prediction steps. The conclusion shows that when the prediction step is 1, the mean absolute percentage error (MAPE) for Guangzhou South station, Xiaolan station and Zhuhai station is 3.97%, 5.83%, and 5.43%, respectively; when the prediction step increases to 2, the MAPE shows an increase trend, which is 5.31%, 6.79%, and 7.62% for Guangzhou South station, Xiaolan station and Zhuhai station, respectively; when the prediction step exceeds 2, the MAPE is stable. In addition, comparative results with other passenger flow prediction methods, i.e., random forest (RF), support vector machine (SVM), gradient boosting (GB), and K-nearest neighbor (KNN) demonstrate that when the prediction step is 1, the SARIMA model performs slightly better; when the prediction step exceeds 2, the MAPE of RF, SVM, GB, and KNN increases dramatically, amounting several times that of the SARIMA model. Finally, the experiment results show that the SARIMA model can achieve a better performance than other models in terms of the multi-step prediction for passenger flow time series.
-
图 2 各车站日均发送客流量
Figure 2. Distribution of average daily passengers departing from each station
图 3 车站客流周期性分布特征
Figure 3. Periodic distribution of daily passengers departing from each station
图 4 车站节假日客流分布特征
Figure 4. Distribution of passengers departing from each station during the vacations
图 5 广州南站发送客流量时间序列分解
Figure 5. Decomposition of departing passengers time series at Guangzhou South station
图 6 时间序列自相关与偏自相关
Figure 6. Autocorrelation diagram and partial autocorrelation diagram of passenger time series
图 7 SARIMA（5,0,1）（2,1,2）7残差分布及检验情况
Figure 7. Distribution and test of residual of SARIMA（5,0,1）（2,1,2）7
图 8 预测步长为1时广州南站客流预测值与RMSE分布情况
Figure 8. Prediction result and RMSE distribution of one-step forward forecast at Guangzhou South station
图 9 广州南站不同预测步长MAPE分布情况
Figure 9. MAPE distribution with different forecast steps of Guangzhou South station
图 10 预测步长为1时小榄站与珠海站客流预测值与RMSE分布情况
Figure 10. Prediction result and RMSE distribution of one-step forward forecast at Xiaolan and Zhuhai station
表 1 原始序列的ADF平稳性检验
Table 1. ADF test of the original time series
统计量 临界值 显著性 P 值 1%水平 5%水平 10%水平 −3.509 8 −3.447 1 −2.868 9 −2.570 7 0.007 7 
下载: 导出CSV
表 2 一阶季节性差分序列ADF检验结果
Table 2. ADF test of first-order seasonal difference sequence
统计量 临界值 显著性 P 值 1%水平 5%水平 10%水平 −5.588 0 −3.444 2 −2.867 5 −2.570 0 0.000 001
下载: 导出CSV
表 3 Ljung-Box检验结果
Table 3. Results of Ljung-Box test
滞后量 相关系数 统计量 显著性 P 值 1.0 −0.020 909 0.179 688 0.671 642 2.0 −0.031 391 0.585 691 0.746 138 3.0 −0.026 921 0.885 028 0.829 039 4.0 0.007 576 0.908 794 0.923 296 5.0 0.003 262 0.913 212 0.969 258 6.0 0.026 582 1.207 246 0.976 525 7.0 −0.005 190 1.218 483 0.990 495 8.0 0.019 373 1.375 445 0.994 588 9.0 0.012 077 1.436 592 0.997 590 10.0 −0.052 022 2.574 035 0.989 752 11.0 0.018 233 2.714 121 0.993 990 12.0 0.066 690 4.592 856 0.970 216 13.0 0.029 064 4.950 590 0.976 265 14.0 −0.051 118 6.060 014 0.964 956 15.0 −0.028 291 6.400 705 0.972 203 16.0 −0.131 306 13.758 166 0.616 724 17.0 −0.037 413 14.357 022 0.641 688 18.0 −0.063 751 16.100 248 0.585 551 19.0 0.038 014 16.721 674 0.608 717 20.0 0.054 497 18.002 092 0.587 270
下载: 导出CSV
表 4 不同车站客流SARIMA预测模型参数
Table 4. SARIMA parameters of different stations
车站 模型参数 AIC 值 小榄 ${\rm{SARIMA}}\left( {3,1,1} \right){\left( {2,0,0} \right)_7}$ 6 017.504 36 珠海 ${\rm{SARIMA}}\left( {3,1,1} \right){\left( {1,0,1} \right)_7}$ 6 348.004 67
下载: 导出CSV
-
PENGPENG J, RUIMIN L, TUO S, et al. Three revised Kalman filtering models for short-term rail transit passenger flow prediction[J]. Mathematical Problems in Engineering, 2016, 795: 1-10. 李夏苗,黄桂章,汤杰. 基于OD反推模型预测客运通道客流量[J]. 铁道学报,2008,30(6): 7-12. doi: 10.3321/j.issn:1001-8360.2008.06.002LI Xiamiao, HUANG Guizhang, TANG Jie. Passenger flow forecasting based on OD-matrix estimation model[J]. Journal of the China Railway Society, 2008, 30(6): 7-12. doi: 10.3321/j.issn:1001-8360.2008.06.002 朱子虎,翁振松. 基于混沌理论的铁路客货运量预测研究[J]. 铁道学报,2011,33(6): 5-11. doi: 10.3969/j.issn.1001-8360.2011.06.001ZHU Zihu, WENG Zhensong. Railway passenger and freight volume forecasting based on chaos theory[J]. Journal of the China Railway Society, 2011, 33(6): 5-11. doi: 10.3969/j.issn.1001-8360.2011.06.001 刘琳玥. 基于PCA-BP神经网络的铁路客运量预测模型研究[J]. 综合运输,2016(8): 43-47.LIU Linyue. Research of railway passenger volume forecast model based on PCA-BP neural network[J]. China Transportation Review, 2016(8): 43-47. WANG Y, ZHENG D, LUO S M, et al. The research of railway passenger flow prediction model based on BP neural network[J]. Advanced Materials Research, 2013, 605: 2366-2369. TSAI T H, LEE C K, WEI C H. Neural network based temporal feature models for short-term railway passenger demand forecasting[J]. Expert Systems with Applications, 2009, 36(2): 3728-373. doi: 10.1016/j.eswa.2008.02.071 李立. 济南至青岛高速铁路客运量预测研究[J]. 铁道运输与经济,2016,38(9): 45-49.LI Li. Traffic volume forecast for Ji’nan-Qingdao high-speed railway[J]. Railway Transport and Economy, 2016, 38(9): 45-49. JIANG X, ZHANG L, CHEN X. Short-term forecasting of high-speed rail demand:a hybrid approach combining ensemble empirical mode decomposition and gray support vector machine with real-world applications in China[J]. Transportation Research, Part C, 2014, 44(4): 110-127. 王莹,韩宝明,张琦,等. 基于SARIMA模型的北京地铁进站客流量预测[J]. 交通运输系统工程与信息,2015,15(6): 205-211. doi: 10.3969/j.issn.1009-6744.2015.06.031WANG Ying, HAN Baoming, ZAHNG Qi, et al. Forecasting of entering passenger flow volume in Beijing subway based on SARIMA model[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(6): 205-211. doi: 10.3969/j.issn.1009-6744.2015.06.031 何九冉,四兵锋. ARIMA-RBF模型在城市轨道交通客流预测中的应用[J]. 山东科学,2013,26(3): 75-81.HE Jiuran, SI Bingfeng. Application of an ARIMA-RBF model in the forecast of urban rail traffic volume[J]. Shandong Science, 2013, 26(3): 75-81. 成诚,杜豫川,刘新. 考虑节假日效应的交通枢纽客流量预测模型[J]. 交通运输系统工程与信息,2015,15(5): 202-207. doi: 10.3969/j.issn.1009-6744.2015.05.029CHENG Cheng, DU Yuchuan, LIU Xin. A passenger volume prediction model of transportation hub considering holiday effects[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(5): 202-207. doi: 10.3969/j.issn.1009-6744.2015.05.029 白丽. 城市轨道交通常态与非常态短期客流预测方法研究[J]. 交通运输系统工程与信息,2016,17(1): 127-135.BAI Li. Urban rail transit normal and abnormal short-term passenger flow forecasting method[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 17(1): 127-135. 孙湘海,刘潭秋. 基于神经网络和SARIMA组合模型的短期交通流预测[J]. 交通运输系统工程与信息,2008,8(5): 32-37. doi: 10.3969/j.issn.1009-6744.2008.05.006SUN Xianghai, LIU Tanqiu. Short-term traffic flow forecasting based on a hybrid neural network model and SARIMA model[J]. Journal of Transportation Systems Engineering and Information Technology, 2008, 8(5): 32-37. doi: 10.3969/j.issn.1009-6744.2008.05.006 蔡昌俊,姚恩建,王梅英,等. 基于乘积ARIMA模型的城市轨道交通进出站客流量预测[J]. 北京交通大学学报,2014,38(2): 135-140. doi: 10.11860/j.issn.1673-0291.2014.04.24CAI Changjun, YAO Enjian, WANG Meiying, et al. Prediction of urban railway station’s entrance and exit passenger flow based on multiply ARIMA model[J]. Journal of Beijing Jiaotong University, 2014, 38(2): 135-140. doi: 10.11860/j.issn.1673-0291.2014.04.24 JIA Y, HE P, LIU S, et al. A combined forecasting model for passenger flow based on GM and ARMA[J]. International Journal of Hybrid Information Technology, 2016, 9(2): 215-226. doi: 10.14257/ijhit.2016.9.2.19 王燕. 应用时间序列分析[M]. 中国人民大学出版社, 2005: 65-66. -
下载:
点击查看大图
计量
- 文章访问数: 686
- HTML全文浏览量: 364
- PDF下载量: 56
- 被引次数: 0