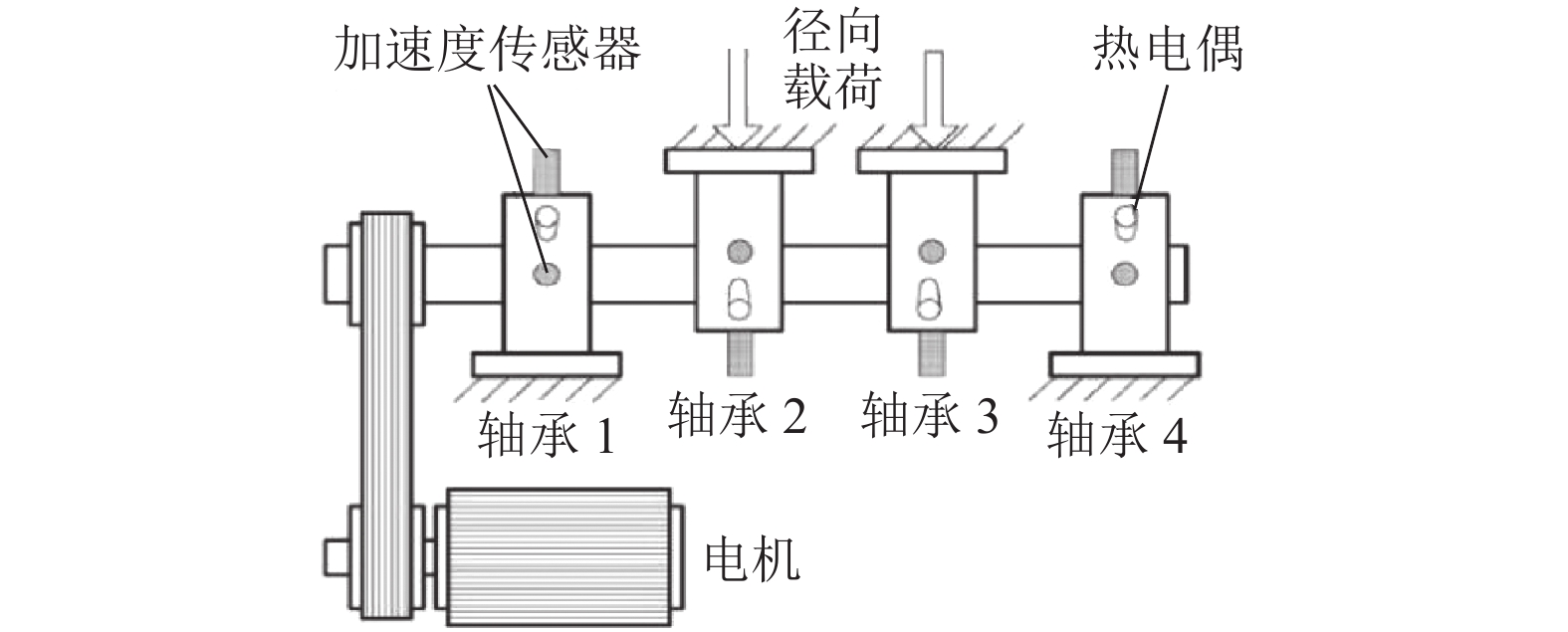
Condition Monitoring of Axle Box Bearing Based on Improved Safety Region
-
摘要: 为了提高高速列车轴箱轴承的运行可靠性，将安全域理论引入到轴承的状态监测，并将传统安全域估计转化为确定安全域的边界值来避免复杂模型参数的影响；利用归一化内禀模态分量的能量距构建轴承运行的状态特征向量，根据关联函数建立轴承安全域边界值估计模型，采用粒子群优化算法进行寻优求解；基于求解结果，结合关联函数定量分析轴承的运行状态，利用轴承全寿命疲劳试验进行验证，并将该方法应用于轴箱轴承的状态监测. 研究结果表明：全寿命试验的轴承运行状态的检出率和分类正确率分别为0.951和0.939；高速列车轴箱轴承运行状态的分类正确率为0.935，轴承运行正常，与其实际状态相一致.Abstract: To improve the operating reliability of the axle box bearing of high-speed trains, the safety region theory was introduced into condition monitoring of the axle box bearing. The traditional assessment of the safety region was transformed into determining the boundary values, aiming to avoid the influence of complex model parameters on the evaluation process of the safety region. The normalized energies of intrinsic mode functions were used to construct the eigenvector of bearing operating state, and the correlation function was used to establish the evaluation model of the safety region boundary values, where the particle swarm optimization algorithm was adopted to get optimal solution. On the basis of estimation results of boundary values, correlation function was utilized to assess the operating state of bearing quantitatively. The effectiveness was verified by the fatigue test of rolling bearing, and the method was used for condition monitoring of the axle box bearing. The results show that the detection rate and classification rate of bearing operating state of fatigue test are 0.951 and 0.939, respectively; the classification rate of operating state of the axle box bearing is 0.935, indicating that the axle box bearing is running normally, which is consistent with its actual operating state.
-
图 6 不同样本数量下的轴承运行状态分布
Figure 6. Operating state distribution of bearing under different sample sizes
表 1 相关系数均值
Table 1. Mean values of correlation coefficients
分量 IMF1 IMF2 IMF3 IMF4 IMF5 IMF6 均值 0.737 0.474 0.490 0.243 0.150 0.130 分量 IMF7 IMF8 IMF9 IMF10 r 均值 0.187 0.111 0.016 0.006 0.006 
下载: 导出CSV
表 2 安全域边界值
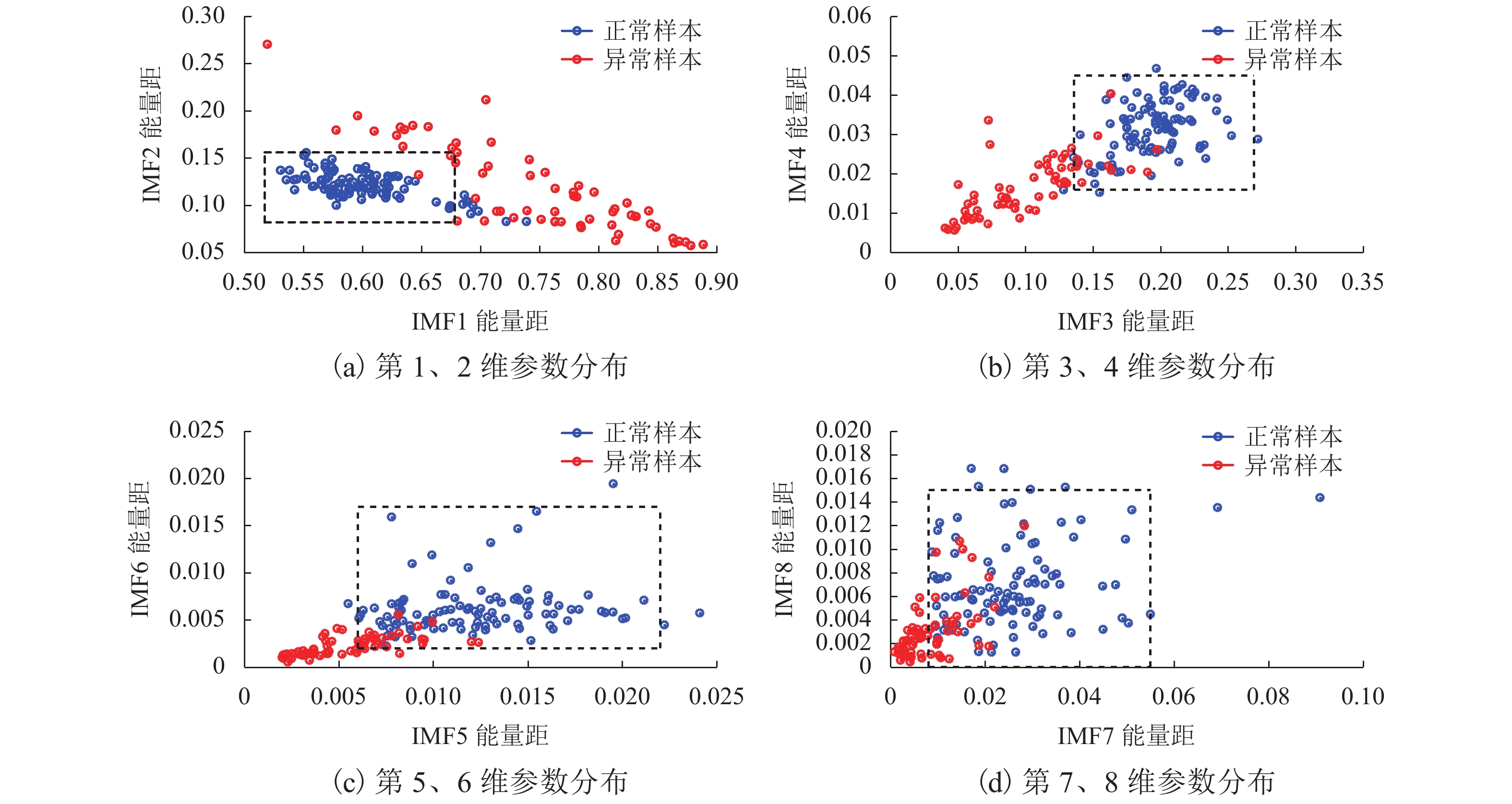
Table 2. Boundary values of safety region
分量名称 上界 下界 IMF1 0.517 0.678 IMF2 0.082 0.156 IMF3 0.136 0.269 IMF4 0.016 0.045 IMF5 0.006 0.022 IMF6 0.002 0.017 IMF7 0.008 0.055 IMF8 0.000 0.015
下载: 导出CSV
表 3 轴承运行状态分类结果及系统运行时间
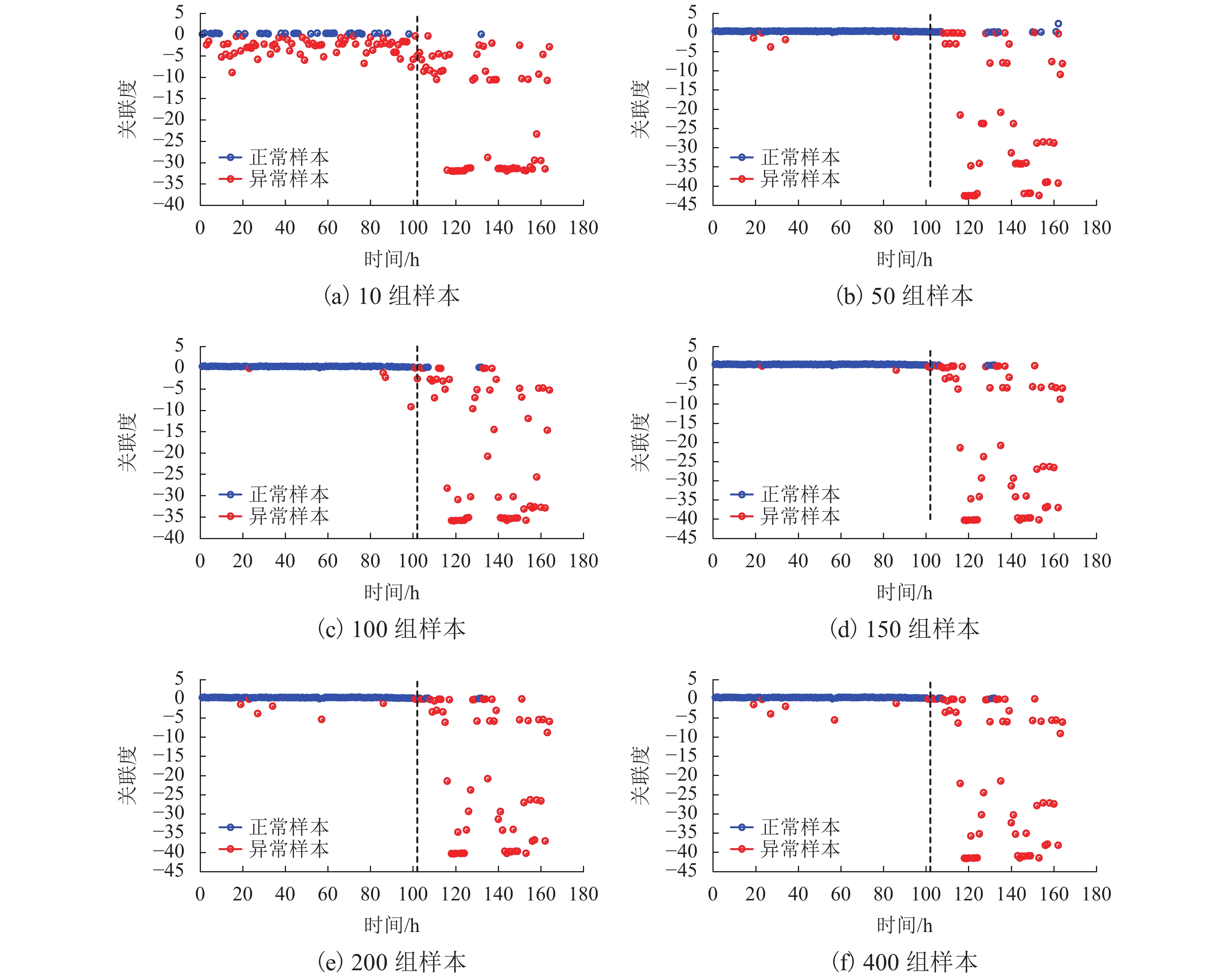
Table 3. Classification results of bearing operating state and system running time
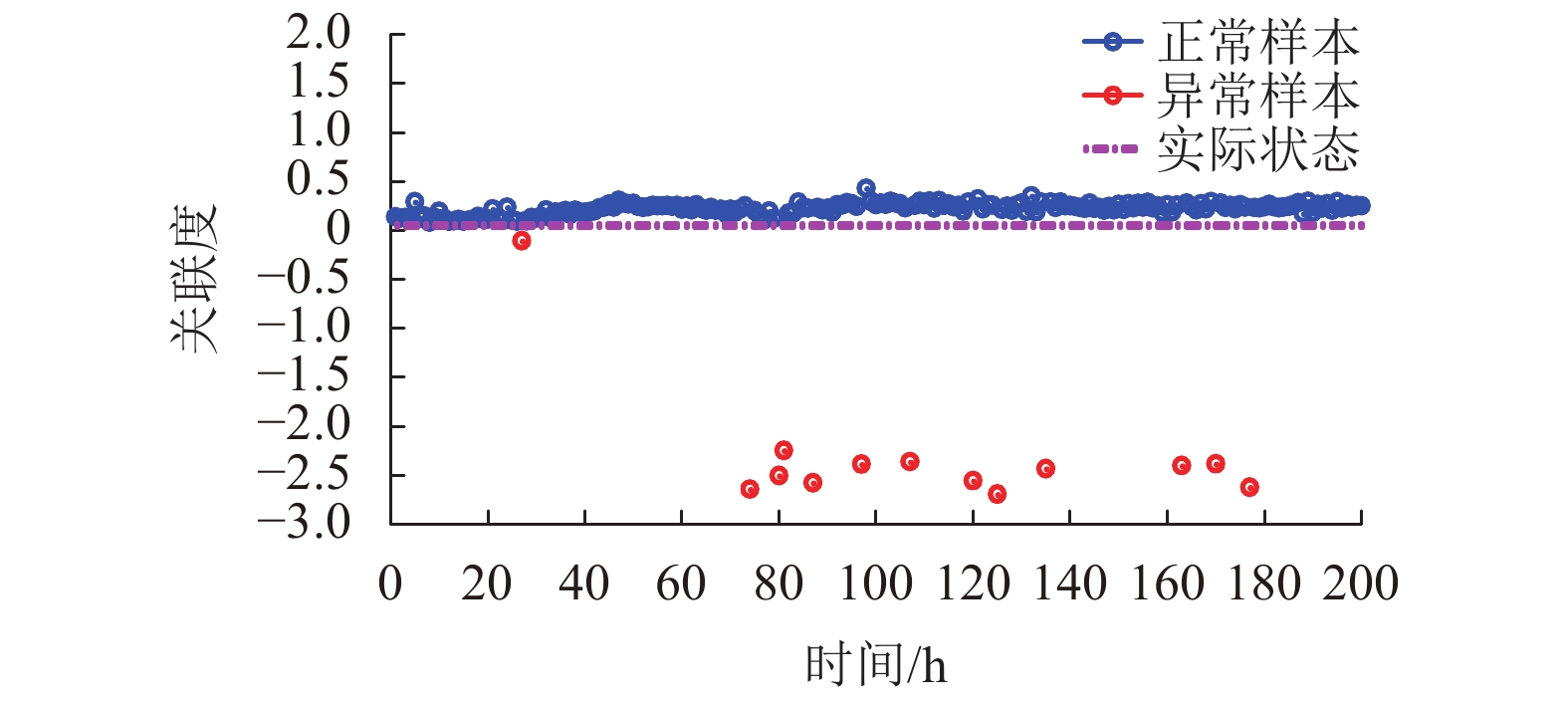
项目 10 组 50 组 100 组 150 组 200 组 400 组 检出率 0.343 0.872 0.951 0.941 0.951 0.951 分类正确率 0.585 0.890 0.939 0.939 0.940 0.938 运行时间/s 40 190 627 988 1 355 2 528
下载: 导出CSV
-
YU Jianbo. Bearing performance degradation assessment using locality preserving projections[J]. Expert Systems with Applications, 2011, 38(6): 7440-7450. doi: 10.1016/j.eswa.2010.12.079 赵聪聪. 高速列车传动系统可靠性分析与评估[D]. 长春: 吉林大学, 2016. ZHANG Yuan, QIN Yong, XING Zongyi, et al. Roller bearing safety region estimation and state identification based on LMD-PCA-LSSVM[J]. Measurement, 2013, 46(3): 1315-1324. doi: 10.1016/j.measurement.2012.11.048 WU F F, KUMAGAI S. Steady-state security regions of power systems[J]. IEEE Transactions on Circuits and Systems, 1982, 29(11): 703-711. doi: 10.1109/TCS.1982.1085091 刘志亮,刘仕林,李兴林,等. 滚动轴承安全域建模方法及其在高速列车异常检测中的应用[J]. 机械工程学报,2017,53(10): 116-124. doi: 10.3901/JME.2017.10.116LIU Zhiliang, LIU Shilin, LI Xinglin, et al. Safety domain modelling of rolling bearing and its application to anomaly detection for high-speed rail vehicles[J]. Journal of Mechanical Engineering, 2017, 53(10): 116-124. doi: 10.3901/JME.2017.10.116 冯坚强,李俊明,王晓浩,等. 基于LSSVM和PNN的车轮状态安全域估计及故障诊断[J]. 机械制造与自动化,2017,46(1): 141-145.FENG Jianqiang, LI Junming, WANG Xiaohao, et al. Safety region estimation and fault diagnosis of wheels based on least squares support vector machine and probabilistic neural networks[J]. Machine Building & Automation, 2017, 46(1): 141-145. HE Yongxiu, DAI Aiying, ZHU Jiang, et al. Risk assessment of urban network planning in china based on the matter-element model and extension analysis[J]. International Journal of Electrical Power and Energy Systems, 2011, 33(3): 775-782. doi: 10.1016/j.ijepes.2010.12.037 WANG Chunlai, WU Aixiang, LU Hui, et al. Predicting rockburst tendency based on fuzzy matter—element model[J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 75(2): 224-232. 刘玉梅,赵聪聪,熊明烨,等. 高速列车传动系统特征参数经典域优化[J]. 西南交通大学学报,2016,51(1): 85-90,120. doi: 10.3969/j.issn.0258-2724.2016.01.013LIU Yumei, ZHAO Congcong, XIONG Mingye, et al. Optimization of classical domains for high-speed train transmission system[J]. Journal of Southwest Jiaotong University, 2016, 51(1): 85-90,120. doi: 10.3969/j.issn.0258-2724.2016.01.013 BEN A J, FNAIECH N, SAIDI L, et al. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals[J]. Applied Acoustics, 2015, 89(3): 16-27. WANG C F, AN G, YANG F J. Research on fault diagnosis of certain armored vehicle’gear-box with IMF’s energy moment[J]. Advanced Materials Research, 2011, 383(11): 248-253. QIU H, LEE J, LIN J, et al. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics[J]. Journal of Sound and Vibration, 2006, 289(1): 1066-1090. LIU Y M, ZHAO C C, XIONG M Y, et al. Assessment of bearing performance degradation via extension and EEMD combined approach[J]. Journal of Central South University, 2017, 24(5): 1155-1163. doi: 10.1007/s11771-017-3518-5 陶新民,徐晶,杨立标,等. 基于GARCH模型MSVM的轴承故障诊断方法[J]. 振动与冲击,2010,29(5): 11-15. doi: 10.3969/j.issn.1000-3835.2010.05.003TAO Xinmin, XU Jing, YANG Libiao, et al. Study of bearing fault diagnosis based on GARCH model[J]. Journal of Vibration and Shock, 2010, 29(5): 11-15. doi: 10.3969/j.issn.1000-3835.2010.05.003 -
下载:
点击查看大图
图(8) / 表(3)
计量
- 文章访问数: 650
- HTML全文浏览量: 255
- PDF下载量: 10
- 被引次数: 0