Static Bearing Capacity Analysis of CFRP-Reinforced Short CHS Steel Tubular Columns under Axial Compression
-
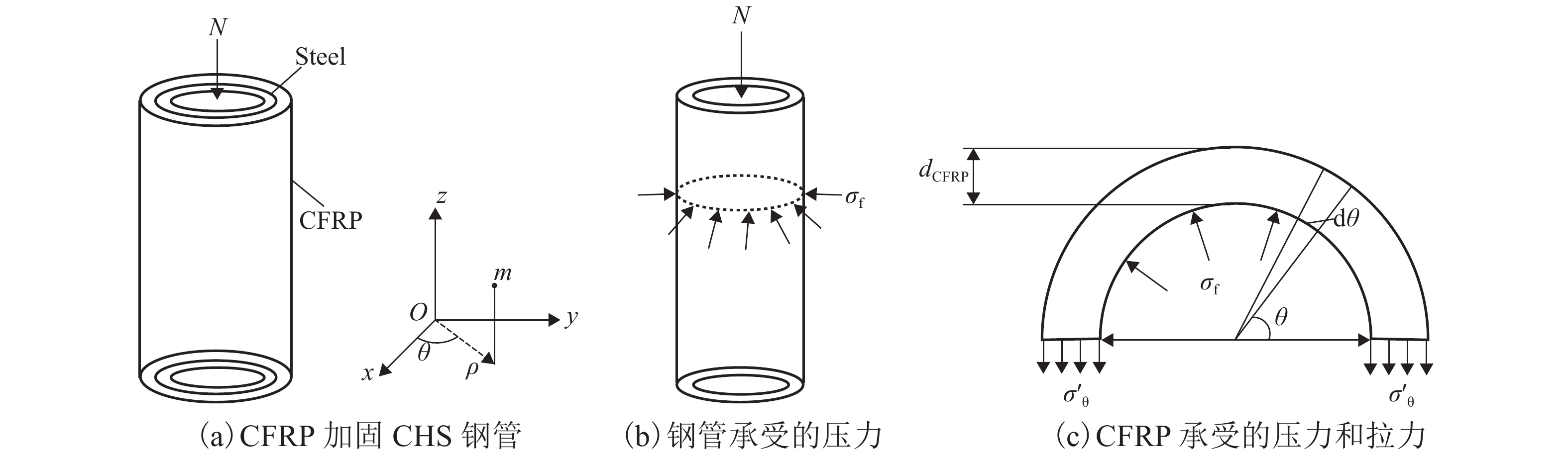
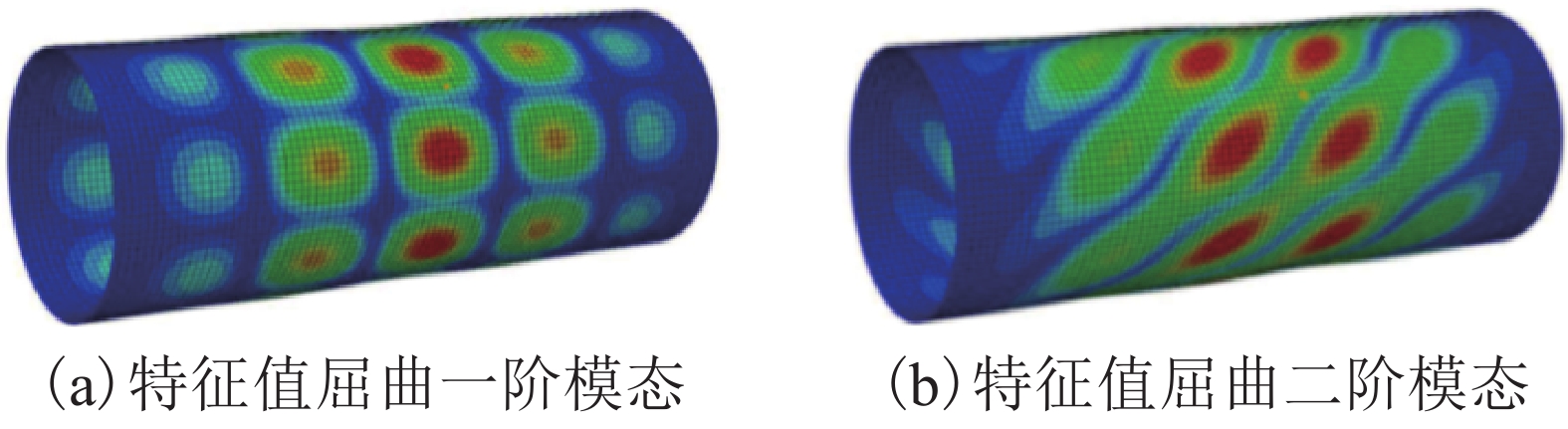
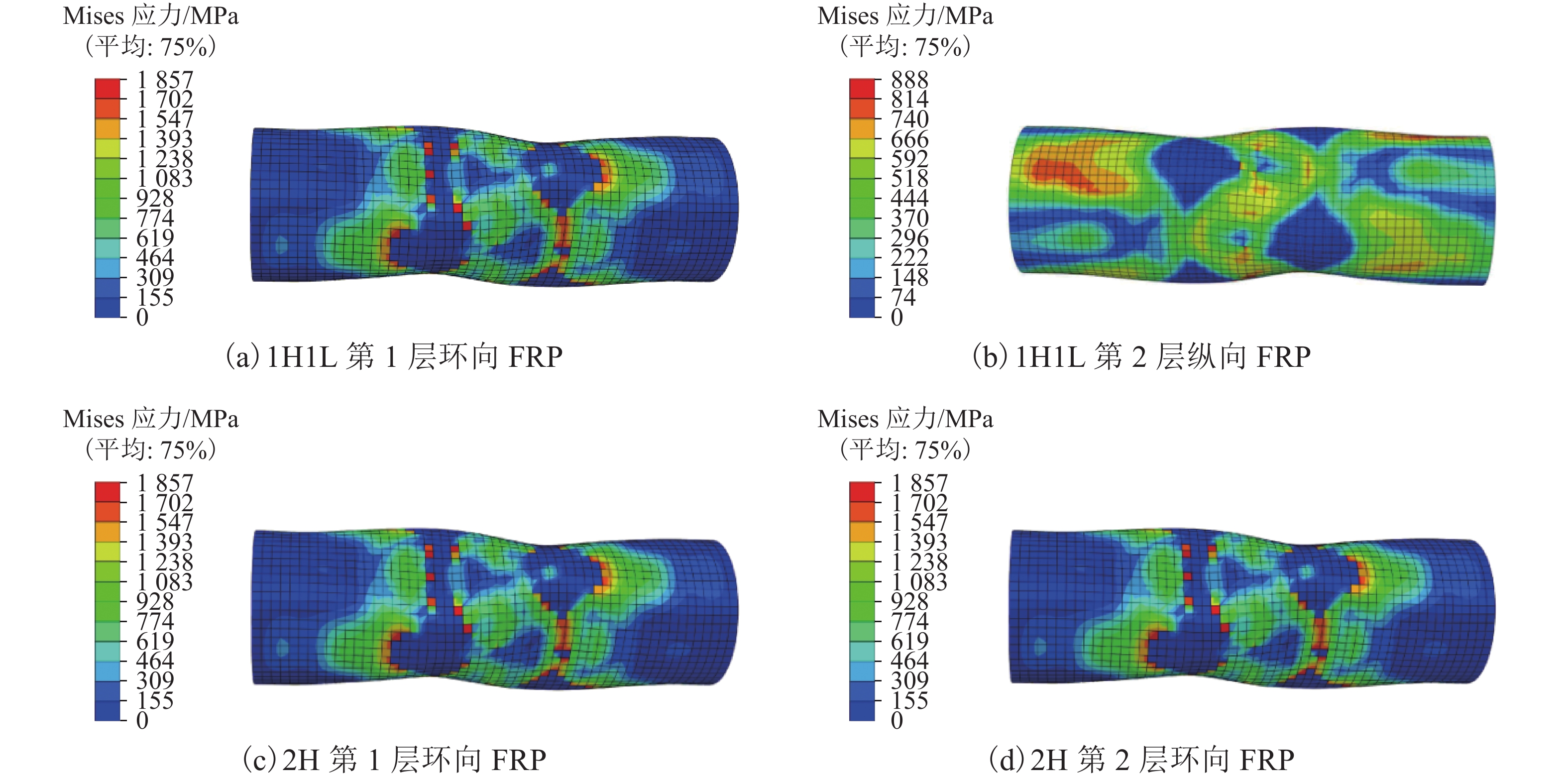
摘要: 为了研究轴压作用下碳纤维增强复合材料（carbon fibre-reinforced polymer，CFRP）加固圆形空心截面（circular hollow section，CHS）钢管短柱的极限承载力，对轴压作用下CFRP加固CHS钢管短柱进行了理论和数值分析. 理论分析中，利用等效截面法推导了两种不同粘贴方式（全环向粘贴以及环向和纵向交替粘贴）的CFRP加固圆钢管短柱在轴压作用下静力承载力的理论计算公式；数值分析中，将特征值屈曲与Riks法相结合建立了轴压作用下CFRP加固圆钢管短柱的非线性有限元分析模型. 对该模型中的环向和纵向CFRP进行应力分析后发现，环向CFRP处于拉伸状态，约束钢管的径向变形；纵向CFRP会承担轴压荷载中的部分压力，限制钢管的变形. 最后，将所建立的有限元分析模型结果和所推导的理论公式结果与已有文献的试验结果进行对比，发现三者之间的最大误差不超过2%，验证了建立的有限元模型和所推导的理论公式分析结果的准确性.
-
关键词:
- CFRP加固圆钢管短柱 /
- 轴压作用 /
- 静力承载力 /
- 等效截面法 /
- 有限元分析
Abstract: To predict the ultimate strength of a short circular hollow section (CHS) steel tubular columns reinforced with carbon fibre-reinforced polymer (CFRP), both theoretical and numerical analyses were carried out. In the theoretical analysis, based on equivalent section method, the equations for calculating the load bearing capacities of CHS steel tubular columns under axial compression are deduced, which correspond to two different reinforcing methods, in which CFRPs are arranged in circumferential placement and in longitudinal-circumferential placement. In the numerical analysis, both eigenvalue buckling method and Riks method are combined to build a nonlinear finite element model of the tubular columns under axial compression. The finite element analysis for the stress distribution of the longitudinal and circumferential CFRPs shows that the circumferential CFRPs are under tension and restrain the radial deformation of the tubular columns, while the longitudinal CFRPs share the axial compression and restrain the deformation of the tubular columns. The comparison of the numerical results, theoretical results and reported experimental results show that the maximum deviation among them is no more than 2%, which verifies the finite element model and deduced equations. -
西部山区地形复杂、地质条件恶劣、地震频发，强降雨和堰塞湖溃坝、水库泄洪往往会产生洪水，对重现期较短的大量中小跨度梁桥造成严重水毁破坏. 20世纪中后期我国桥梁水毁数量巨大，这里不再详述[1]. 仅据新闻媒体报道，每年雨季洪水导致数以千计的简支梁桥遭到不同程度的破坏，带来数亿元的直接经济损失. 如2018年11月，金沙江白格堰塞湖泄洪，下游竹巴龙金沙江大桥等7座桥梁被冲毁. 美国调查了该国1989—2000年桥梁破坏原因，结果表明该国约50%的桥梁失效是由于水力荷载导致的[2].
桥梁的水毁破坏已引起世界各国的广泛关注[3]，我国在20世纪50年代末开始了桥涵水文方面的研究工作. 1983年Naudascher等[4]通过理论和试验研究了明渠中桥面板的动水力以及由于桥面板的阻塞引起的水头损失等. 重庆交通学院肖盛燮团队[5-9]开展了洪水冲击简支板梁和拱桥的模型试验，推导了山洪冲击下梁体（板梁）水平作用力、竖向作用力以及它们的修正系数，并对梁桥和拱桥的抗洪机理和计算模型进行了研究. 2001年张辉[10]结合实际板梁桥受力特性，推导了桥梁在洪水冲击下水平、竖向作用力计算公式，并提出了几种典型的失效模式. 2003年Malavasi等[11]通过模型试验研究了矩形桥面板的水动力荷载，测量了不同淹没深度和Froude数下桥面板上水动力时程曲线，研究表明自由液面的影响不可忽视. 2009年Kerenyi等[12]对淹没T梁开展了模型试验和数值模拟，提出了水流力计算系数的建议取值. 2015年邵鹏[13]计算了洪水对桥梁的水平与竖向作用，分析了简支单箱式箱型梁桥在洪水冲击下的破坏特征与失效机制，研究了洪水流速及其变异性、桥梁淹没水位等关键参数对桥梁可靠度的影响. 2016年庄一舟等[14]研究了整体式桥台无伸缩缝桥梁抗洪性能，当跨度大于两跨时，整体式桥台无缝桥梁在洪水作用下弹性阶段的受力性能优于普通有缝桥梁. 2018年吴安杰等[15]研究了洪水对不同截面形式桥墩冲击过程，发现冲击放大系数随着水位高度的增加而增大. 2020年杨万理等[16]通过对桥墩三维绕流精细化的研究，发现圆柱表面动水压强沿水深不均匀分布.
我国现役桥梁中存在大量简支T梁和简支小箱梁桥，当这些梁桥被洪水淹没后，横隔板与梁体所形成的腔室内的空气将被裹挟在腔室内，可能对梁桥上部结构安全造成不利影响. 实心防撞护栏在梁桥上的应用也比较常见，在洪水翻越实心护栏前，实心护栏与桥面板顶部围成的空间内的空气所产生的浮力，也可能给桥梁上部结构安全带来不利影响. 但是，由上述空气带来的不利影响，在现有文献中未得到充分考虑，梁桥上部结构水毁破坏机理仍缺乏深入研究. 本文将以竹巴龙金沙江大桥为背景，考虑T梁底部横隔板内裹挟空气的影响，研究简支T梁洪水作用力特征和破坏机理，以期为桥梁抗洪措施研究、桥梁抗洪规范完善提供参考.
1. 工程背景和数值计算模型
1.1 竹巴龙金沙江大桥及其简化模型
2018年11月13日白格堰塞湖泄洪，洪水冲毁竹巴龙金沙江大桥，导致318国道中断，如图1所示. 位于该桥上游约470 m处的巴塘水文站记录了洪峰通过期间流量变化. 根据流量和该桥桥位处地形，估算了梁体淹没深度（以梁体底部为参照）与断面平均流速之间的关系，如图2所示. 可见，洪水淹没梁体的最大深度达到15.91 m，这与媒体报道的洪水水面高出桥面12 m[17]（梁底距桥面约2 m，即淹没深度约14 m）吻合较好，证明了图2中断面平均流速与淹没深度的可靠性. 竹巴龙金沙江大桥是9跨简支梁桥，每跨30 m，第1跨、第9跨是板梁，第2～8跨每跨均由4片T梁组成，T梁跨中断面如图3所示. 图中：C为质心；
$ {F}_{\mathrm{D}} $ 、$ {F}_{\mathrm{L}} $ 、${M}_{\mathrm{Z}}$ 和$ {M}_{\mathrm{C}\mathrm{}} $ 分别为梁所受水平力、竖向力、绕下游角点的倾覆弯矩和绕质心的倾覆弯矩；$ S $ 为梁体高度；$ W $ 为上部结构宽度；$ {h}_{\mathrm{b}} $ 为梁底到河床的距离；$ {h}_{\mathrm{u}} $ 为自由液面到河床的距离.
图 1 白格堰塞湖泄洪冲毁竹巴龙金沙江大桥Figure 1. Jinsha River Bridge at Zhubalong destroyed by discharge from Baige landslide dam
图 2 梁体淹没深度与断面平均流速Figure 2. Submergence depth of beam body and average velocity at cross section
图 3 实桥T梁跨中断面（单位：cm）Figure 3. Cross section at middle span of actual T-girder bridge (unit: cm)1.2 水动力系数以及工况设定
洪水作用下桥梁上部结构所受竖向力（
${F}_{\mathrm{L}}$ ）由梁体排开水的体积引起的浮力$（{F}_{\mathrm{L}\mathrm{V}1}）$ 、裹挟空气排开水的体积引起的浮力$（{F}_{\mathrm{L}\mathrm{V}2}）$ 和动水压力竖向分量$（{F}_{\mathrm{L}\mathrm{d}\mathrm{y}}）$ 构成，如式（1）所示.FL=FLV1+FLV2+FLdy. (1) 水平力系数
$ {C}_{\mathrm{D}} $ 、竖向力系数$ {C}_{\mathrm{L}} $ 和倾覆弯矩系数$ {C}_{\mathrm{M}} $ 的定义分别为CD={FD/[0.5ρU2L(hu−hb)]，h∗<1.000,FD/(0.5ρU2SL)，h∗⩾1.000, (2) CL=FL/(0.5ρU2WL)， (3) CM=Mcg/(0.5ρU2W2L)， (4) 式（2）～（4）中：
$ \rho $ 为水的密度；$ U $ 为来流速度；L为梁体轴线方向的长度；$ {h}^{\mathrm{*}} $ 为淹没率，如式（5）所示.h∗=(hu−hb)/S. (5) 当
$ {h}^{*}=0 $ ，水位线刚好位于梁肋底部；当$ {h}^{*}= 1.000 $ ，水位线刚好到达栏杆顶部；当$ {h}^{*} > 1.000 $ ，栏杆被完全淹没. 图2中，洪水从刚淹没T梁底部至达到最大淹没深度经历了约3 h，流速从0.4 m/s增大到2.4 m/s. 可见，洪峰引起液面和流速增大是较为缓慢的过程. 文献[18]表明缩尺模型水流力系数与原型水流力系数基本一致. 为了验证数值计算模型精度并与后期模型试验进行对比，本文以简化后的缩尺模型为研究对象（缩尺比1/20），计算不同时刻（对应特定的淹没率和来流速度）上部结构水流力系数，并由水流力系数反算实桥跨中单位长度上部结构受到的水流力，再分析上部结构破坏机理. 本文计算流体动力学（computational fluid dynamics，CFD）数值模拟工况如表1所示.表 1 CFD数值模拟计算工况Table 1. Cases of CFD numerical simulation工况 $ {h}^{*} $ 流速/(m•s−1) 工况 $ {h}^{*} $ 流速/(m•s−1) C1 0.336 0.136 C10 1.342 0.235 C2 0.671 0.190 C11 1.678 0.250 C3 0.805 0.212 C12 2.013 0.275 C4 0.872 0.223 C13 2.349 0.295 C5 0.889 0.226 C14 2.685 0.316 C6 0.906 0.229 C15 3.02 0.335 C7 0.940 0.235 C16 3.691 0.380 C8 0.973 0.242 C17 4.362 0.438 C9 1.007 0.248 C18 5.369 0.532 2. 数值计算方法
2.1 基本控制方程
本文采用ANSYS Fluent求解雷诺平均纳维-斯托克斯（RANS）方程，其中质量守恒方程和动量方程分别如式（6）和式（7）所示.
∂ui∂xi=0， (6) ρ∂ˉui∂t+ρˉuj∂ˉui∂xj=−∂ˉp∂xj+μ∂2ˉui∂xi∂xj−∂(ρˉuiˉui)∂xj, (7) ˉui=1Δt∫t0+Δtt0uidt， (8) 式中：xi、xj为位移，i，j为笛卡尔坐标系O-xyz的方向指标；ui、
${\bar{u}}_{i}$ 分别为方向i的瞬时速度和时间平均速度；t为时间；t0为起始时刻； $ \Delta t $ 为时间步长；$\bar{p}$ 为时间平均压强；$ \mu $ 为水体的动力黏度.数值模拟包含了空气和水体两种不同的流体，采用VOF （volume of fluid）模型对两种流体的交界面进行追踪. 本文工况中雷诺数较大，数值模拟中采用RNG k-ε湍流模型[19].
梁体边界层采用 Scalable wall function以避免在网格细化过程中第1层网格无量纲厚度
$ {y}^{ + } $ 过小时导致的标准壁面函数退化，$ {y}^{ + } $ 如式（9）所示.y+=dμ√ρτw， (9) 式中：
$d$ 为墙边界到最里层网格中心之间的距离；$ {\tau }_{w} $ 为壁面剪应力.2.2 计算模型
CFD仿真分析所建立的桥梁节段三维几何模型如图4（a）所示，节段模型沿桥轴向的宽度10 cm. 图中增加挡板是为了防止水从桥梁轴向涌上桥面. 三维数值水槽宽度中心剖面如图4（b）所示，该水槽长12 m，宽0.14 m，高2 m，即梁体两侧距离水槽边壁均为2 cm. 水槽上游边界距离桥梁下游侧8.5 m（桥梁宽度的20倍）,下游边界距离桥梁下游侧3.5 m（桥梁宽度的8倍）. 水槽顶部为对称边界，上游边界为压力入口，下游边界为压力出口，底部以及梁体表面设置为无滑移壁面. 将模型上游
$ W $ 、下游$ 2W $ 、护栏顶部上方$ W $ 、梁肋底部下方$ W $ 范围设置为网格划分核心区，其余部分设置为非核心区，如图4所示. 整个计算域都划分为六面体网格，核心区和非核心区之间设置interface连接两侧网格，本文计算工况中$ {y}^{ + } $ 设定为60，核心区内最内层网格厚度$ {d}_{\mathrm{c}\mathrm{b}}=3 $ mm，渐变率为1.1.2.3 数值模型验证、网格无关性以及计算精度验证
采用本团队在西南交通大学深水大跨桥梁实验室开展的模型试验数据验证本文数值计算模型、网格划分方案以及CFD计算中各项参数的合理性. 考虑到计算成本，用于验证的数值模型取试验模型轴向长度的1/8，横截面尺寸保持一致，数值模型与试验模型的淹没率均为1.000，距离模型上游90 cm处流速均为0.3 m/s. 同时新增中等精度网格和精细网格工况以检验网格无关性. 各工况
$ {y}^{ + } $ 取值、核心区边界层网格厚度$ {d}_{\mathrm{c}\mathrm{b}} $ 、网格总数$ N $ 、计算耗时T、阻力系数$ {C}_{\mathrm{D}} $ 、升力系数$ {C}_{\mathrm{L}} $ 如表2所示. 表中各工况中核心区最大网格尺寸$ {d}_{\mathrm{c}\mathrm{m}} $ 均为10 mm，非核心区最大网格尺寸$ {d}_{\mathrm{m}} $ 均为20 mm. 对比发现，CFD计算出的升阻力系数与模型试验吻合比较好，说明了本文数值计算模型、网格划分方案和各项参数设置的合理性. 但是，网格划分越细，计算效率越低. 因此，本文采用表2中粗糙网格划分方式对竹巴龙大桥几何模型进行网格划分.表 2 网格划分精细程度对数值模拟计算精度和计算效率的影响Table 2. Influence of grids generation accuracy on calculation precision and efficiency of numerical simulation工况 y+ dcb/mm N/个 T/h CD CL 模型试验 1.250 −1.240 粗糙 60 3 413086 11 1.176 −1.259 中等 45 2 507650 23 1.224 −1.124 精细 30 1 701862 36 1.238 −1.157 3. 上部结构水流力特点
图5以淹没率
$ {h}^{*}= $ 0.805, 1.000, 1.678的工况为代表，展示了流场稳定后上部结构受到的水平力、竖向力和绕上部结构质心转动的倾覆弯矩时程曲线. 图6展示了$ {h}^{*}=1.678 $ 工况梁体周围的压力云图和涡量图. 淹没率$ {h}^{*}\leqslant 1.000 $ 时，来流速度较小，上部结构受到的水平力、竖向力和倾覆弯矩波动都很小，基本为一条直线；当淹没率较大时，来流速度也较大，如工况$ {h}^{*}=1.678 $ ，水平力和绕质心的倾覆弯矩都出现明显的波动，这主要是由上部结构下游一侧漩涡脱落引起的，如图6（b）所示. 水平力主要由上部结构上游迎水面与下游背水面受到的压差决定；竖向力由上部结构底部与顶部的压差决定，被淹没的梁体和裹挟空气产生的浮力起支配作用；绕质心的倾覆弯矩主要受到梁体正上方、正下方漩涡的水平位置的影响. 当$ {h}^{*}=1.000 $ 时，上部结构底部靠近上游的漩涡形成的低压区使得倾覆弯矩为负值，如图6（a）所示；当$ {h}^{*} > 1.000 $ 时，自由液面的影响逐渐减小，梁体正上方和正下方边界条件逐渐变得对称，梁体正上方和正下方漩涡发展愈发充分，漩涡脱落愈发显著，因此倾覆弯矩时程曲线出现了明显波动，如图5所示.
图 5$ {h}^{\mathrm{*}}= $ 0.805,1.000,1.678时水流力时程曲线Figure 5. Time histories of flow force for cases with$ {\mathit{h}}^{\mathit{*}}= $ 0.805, 1.000 and 1.678
图 6 工况h* = 1.678中t = 1413.894 s时刻云图Figure 6. Contour of case with h* = 1.678 at t = 1413.894 s4. 简支T梁桥上部结构破坏机理分析
数值模拟发现，当
$ 0.889 < {h}^{*} < 1.000 $ 时，护栏上游产生的壅水高度将高于护栏顶部，如果计算时间足够长，翻越护栏顶部的壅水将填满护栏内侧. 以工况$ {h}^{*}=0.906 $ 为例，CFD计算显示翻越护栏顶部的壅水将在约20 min后与护栏顶部内侧平齐，即越过护栏的洪水将在约$ 90（\approx 20\sqrt{20}） $ min后达到实桥护栏内侧顶部. 该时长远大于实桥处于该淹没率（$ {h}^{*}=0.906 $ ）和下一个淹没率（$ {h}^{*}=0.940 $ ）之间的间隔（约1 min），即在实际情况下相邻工况之间，仅有少量水体翻越护栏顶部. 本节分两种情形展开讨论：情形1，假设$ 0.889 < {h}^{*} < 1.000 $ 时，没有壅水翻越护栏，研究表1中不同淹没率下T梁受力特征和破坏机理；情形2，假设$ 0.889 < {h}^{*} < 1.000 $ 时，壅水翻越护栏使得护栏内、外侧水位线平齐，分析表1中不同淹没率下T梁受力特征和破坏机理.4.1 情形1：当
$ 0.889 < {h}^{\mathrm{*}} < 1.000 $ 时，壅水不翻越护栏当
$ 0.889 < {h}^{*} < 1.000 $ ，壅水不翻越护栏时，水动力系数随着淹没率变化趋势如图7所示.
图 7 水流力系数随着淹没率$ {h}^{\mathrm{*}} $ 的变化趋势（不考虑壅水漫顶）Figure 7. Variation trend of flow force coefficient with submergence ratio$ {\mathit{h}}^{\mathit{*}} $ (backwater overtopping is not considered)水平力系数
$ {C}_{{\rm{D}}} $ 随着淹没率增大先增大再缓慢减小，并在$ {h}^{*}=1.342 $ 左右取得最大值. 这种变化主要是由于阻水率随着淹没率的增大而逐渐增大，当完全淹没后保持不变引起的. 当$ {h}^{*} < 1.000 $ 时，竖向力系数随$ {h}^{*} $ 增大迅速增大，这主要是由梁体本身、梁底横隔板腔室以及实心护栏内侧空气排开水的体积逐渐增大引起的. 当$ {h}^{*}=1.000 $ 时，大量壅水漫顶淹没护栏内侧，导致排开水的体积骤减，竖向力系数陡降；当$ {h}^{*}= 1.342 $ 时，竖向力系数有所增加，这是因为在桥面板上方形成了漩涡，该漩涡导致桥面板上方动压减小，从而整个竖向力系数有所增大；当$ {h}^{*} > 1.342 $ 时，竖向力系数逐渐减小，这是因为随着$ {h}^{*} $ 增大，桥面板上、下侧流场逐渐趋于对称，动压趋于相同，升力系数逐渐趋近于桥面板本身和裹挟空气的浮力所确定的升力系数，即2.5附近. 倾覆弯矩系数与竖向力系数变化趋势基本一致，不再赘述. 由此可见，竖向力是倾覆弯矩的主要贡献者.沿桥轴线方向取实桥单位长度上部结构作为研究对象，该节段所受到的洪水作用力
$ {F}_{\mathrm{D}} $ 、$ {F}_{\mathrm{L}} $ 和${M}_{\mathrm{Z}}$ 可通过图7中水流力系数来计算. 相应抗力表示为水平抗力${F}_{\mathrm{D}}'$ ，竖向抗力${F}_{\mathrm{L}}'$ ，抗倾覆弯矩${M}_{\mathrm{Z}}'$ .${F}_{\mathrm{D}}'= {0.25F}_{\mathrm{Z}}$ ，其中，${F}_{\mathrm{Z}}=G-{F}_{\mathrm{L}}$ ，G为节段自重，静摩擦系数取值为0.25[19]；${F}_{\mathrm{L}}'=G$ ；${M}_{\mathrm{Z}}'=GE$ ，$ E $ 为质心到旋转中心的水平距离. 当${F}_{\mathrm{D}} > {F}_{\mathrm{D}}'$ ，$ {F}_{\mathrm{L}} > G $ ，${M}_{\mathrm{Z}} > {M}_{\mathrm{Z}}'$ 时，上部结构将分别发生水平位移、上浮和翻转. 不同$ {h}^{*} $ 下节段梁体受到的洪水作用力和抗力变化如图8所示.
图 8 节段梁体洪水作用力和相应的抗力随$ {h}^{\mathrm{*}} $ 变化趋势（不考虑壅水漫顶）Figure 8. Variation trend of flood force and resistance of segmental beam with submergence ratio$ {\mathit{h}}^{\mathit{*}} $ (backwater overtopping is not considered)由图8可知：
1） 总体上节段梁体受到的水平力
$ {F}_{\mathrm{D}} $ 随着淹没率的增大而增大，${F}_{\mathrm{D}}'$ 在$ {h}^{*} < 1.000 $ 时，随着$ {h}^{*} $ 的增大而减小，直至减小为0，在$ {h}^{*}=1.000 $ 时急剧增加，此后基本保持不变（图8（a））.${F}_{\mathrm{D}}'$ 的变化特征直接受到$ {F}_{\mathrm{L}} $ 的影响：$ {F}_{\mathrm{L}} $ 在$ {h}^{*} < 1.000 $ 时随着$ {h}^{*} $ 的增大而增大，在$ {h}^{*}=1 .000$ 时急剧降低至65 kN附近并保持不变（图8（b）），其中，竖向抗力为重力$ G $ , 始终保持不变. 节段梁体倾覆弯矩变化特性与竖向力相似，只是当$ {h}^{*} > 1.000 $ 时倾覆弯矩随着$ {h}^{*} $ 的增大而略有增加，抗倾覆弯矩主要由重力提供，并且始终保持不变（图8（c））.2） 在图8（a）中，当
$ {h}^{*} $ 略大于0.872 （$ {h}^{*}\approx 0.875 $ ）时，将出现${F}_{\mathrm{D}} > {F}_{\mathrm{D}}'$ ，$ {F}_{\mathrm{L}} < G $ ，${M}_{\mathrm{Z}} < {M}_{\mathrm{Z}}'$ ，即此时梁体将向下游发生水平移动. 静摩擦通常情况下大于动摩擦，一旦水平推力克服静摩擦梁体开始运动，梁体必将加速运动并撞击支座防撞挡块.${F}_{\mathrm{D}}'={0.25F}_{\mathrm{Z}}$ 主要来自支座摩擦力，水平抗力变化规律间接反映了梁体所受到的洪水竖向作用力的变化规律，此刻（$ {h}^{*}=0.875 $ ）$ {F}_{\mathrm{L}} $ 非常接近$ G $ ，如图8（b）所示；而${M}_{\mathrm{Z}}$ 更加接近抗${M}_{\mathrm{Z}}'$ ，如图8（c）. 说明此刻（$ {h}^{*}=0.875 $ ）节段梁体有非常明显的上浮和翻转趋势. 如果挡块被梁体撞坏，那么梁体将继续往下游运动，即发生平动落梁：当其重心运动到盖梁外侧时，梁体在继续往下游运动的同时由于自重开始下沉，同时可能发生旋转运动，导致整个梁体倒扣在河底（图9（a））；旋转运动能量也可能不足以让梁体完全翻转，此时梁体将平躺在河底（图9（b））. 如果挡块未能被梁体破坏，挡块的反作用力将暂时阻止梁体在支座上继续水平运动. 但随着淹没深度继续增大，如当$ {h}^{*}= 0.906 $ 时，水平力将进一步增大（图8（a）），竖向力进一步增大后几乎等于梁体重力（图8（b）），即此时梁体开始上浮，支座提供的摩擦阻力变为0，梁体受到的水平力将完全作用在挡块上，将导致挡块破坏，更严重的是，此时梁体的倾覆弯矩也大于抗倾覆弯矩（图8（c）），梁体将绕着挡块与梁体的接触点转动，一旦发生转动，即使转动角度很小，因梁体迎水面积增大，梁体将受到更大的水平力，导致挡块承受巨大的推力而破坏（图9（c））. 此后，梁体发生翻转落梁，即梁体将同时作翻转运动和朝向下游的移动，当梁体重心运动到盖梁外时，梁体在重力作用下下沉，最终梁体翻转后倒扣在河床上（图9（c））. 此处的分析结果与该桥灾后调研呈现的实际破坏状态基本一致，即盖梁上防震挡块都被破坏掉，梁体部分翻转落梁，部分平动落梁，如图10所示.3） 如果支座提供的摩擦力过大梁体在
$ {h}^{*}= 0.906 $ 时刻未发生平移，随着淹没深度的增大，如在$ {h}^{*}=0.940 $ 或$ {h}^{*}=0.973 $ 时刻，梁体将受到远大于自重的向上的竖向力和远大于抗倾覆弯矩的倾覆弯矩，使得梁体上浮和旋转，梁体上浮使得支座脱空、支座摩擦力为零，梁体在水平力作用下必将发生水平运动从而撞击挡块，发生与图9（c）相似的破坏过程.4） 当
$ {h}^{*}=1.000 $ 时，壅水越顶灌入实心护栏内侧，水体自重导致梁体受到竖直向上的水流力急剧减小，水平抗力因此急剧增大，倾覆弯矩急剧减小，洪水作用力将远小于对应的抗力. 因此如果上部结构在$ {h}^{*}\leqslant 1.000 $ 时未破坏，那么该桥在$ {h}^{*}=5.000 $ 之前，都不会被破坏. 当$ {h}^{*}=5.000 $ 时，洪水水平力将再次超过水平抗力，但此时洪水竖向力和倾覆弯矩都远小于它们对应的抗力. 因此，上部结构在该时刻只会发生平移运动而破坏. 相对而言，该桥在$0.872 \leqslant {h}^{*} \leqslant 1.000$ 上部结构被破坏的概率最大.4.2 情形2：当
$0.889\;{ < h}^{\mathrm{*}} < 1.000$ 时，壅水翻越护栏当
$0.889\;{ < h}^{*} < 1.000$ ，壅水翻越护栏并且使得护栏内外侧液面平齐时，阻力系数基本不变，升力系数和倾覆弯矩系数峰值对应的淹没率提前到$ {h}^{*}= 0.872 $ ，分别如图11所示. 此时洪水作用下梁体受到的水平力、竖向力、倾覆弯矩随着淹没率变化趋势如图12所示. 可见，如果考虑${h}^{*} > 0.872$ 壅水翻越护栏，那么在壅水翻越护栏前，上部结构处于最危险的状态，如$ {h}^{*}=0.872 $ 时，水平力和水平抗力几乎相等，竖向力略小于梁体重力，倾覆弯矩略小于抗倾覆弯矩. 灌进护栏内侧的水体自重使得洪水竖向力和倾覆弯矩都急剧减小，水平反力急剧增大，即上部结构变得安全.
图 11 水流力系数随着淹没率$ {h}^{\mathrm{*}} $ 变化趋势（壅水漫顶）Figure 11. Variation of flow force coefficient with submergence ratio$ {\mathit{h}}^{\mathit{*}} $ (backwater overtopping)洪水冲击实桥，水位持续快速上涨. 当
$ 0.872 < {h}^{*} < 1.000 $ 时，栏杆内侧液面高度大于0但小于栏杆外侧液面高度. 因此，实桥上部结构水平力比图12（a）小，但比图8（a）要大，即上部结构会发生水平移动；竖向力比图12（b）大，但比图8（b）要小，即上部结构发生上浮的概率很大；倾覆弯矩比图12（c）大，但比图8（c）要小，即上部结构发生旋转是大概率事件. 总之，洪水冲击实桥时，上部结构会发生如4.1节所讨论的破坏，但是发生破坏的时间可能会因为壅水翻越护栏而有所延迟.可见，该桥水毁破坏的主要原因可以推断为：1） 梁体受到的浮力过大. 经计算，在
$ {h}^{*} $ =0.906，0.940，0.973工况中，实心栏杆和梁顶围成空气体积在壅水灌入前所贡献的浮力分别占梁体洪水竖向力的44%、48%和51%. 在上述3个工况中，梁底横隔板内裹挟空气分别贡献了约18%、17%和16%的竖向力. 2） 梁体受到的水平力过大. 实心栏杆导致水平力大幅增加，实心栏杆在上述3个工况中分别贡献了26%、29%和31%的水平力. 3） 梁体受到的浮力过大，会直接导致梁体上浮；间接导致倾覆弯矩过大，诱发梁体翻转落梁；也会间接导致水平抗力（摩擦阻力）过小，同时考虑到实心栏杆导致的水平力大幅增大，将直接导致梁体发生水平移动.
图 12 节段梁体作用力和相应的抗力随淹没率$ {h}^{\mathrm{*}} $ 变化趋势（壅水漫顶）Figure 12. Variation of flood force and resistance of segmental beam with submergence ratio$ {\mathit{h}}^{\mathit{*}} $ (backwater overtopping)5. 结 论
本文以2018年白格堰塞湖泄洪中被破坏的竹巴龙金沙江大桥为研究对象，考虑实心护栏与桥面板顶部之间的空气，以及T梁底部横隔板形成的腔室中裹挟空气对上部结构的影响，主要结论如下：
1）
$ {h}^{*} < 1.342 $ 时，简支T梁水平力系数随$ {h}^{*} $ 的增大而增大，最大值约为1.9；当$ {h}^{*} > 1.342 $ 时，水平力系数随$ {h}^{*} $ 的增大逐渐减小至约1.4.2） 在壅水翻越护栏前，竖向力系数随着
$ {h}^{*} $ 的增大而逐渐增大，最大值约24；当壅水翻越护栏后，竖向力系数将急剧减小，并随着$ {h}^{*} $ 的继续增大而减小并趋于2.5. 倾覆弯矩系数变化规律与竖向力系数变化规律基本一致.3） 在
$ {h}^{*} $ 接近1.000时，上部结构发生破坏的风险最大. 竹巴龙金沙江大桥破坏过程中上部结构发生水平移动的概率大于上部结构发生上浮和旋转的概率.4） 本桥实心栏杆极大地增大了梁体所受的水平力；实心栏杆和梁顶之间的空气对竖向力的贡献最高达到51%，横隔板间裹挟空气对竖向力的贡献最高达到18%，显著增大了梁体的竖向力和以及倾覆弯矩，显著减小了水平抗力. 实心栏杆和裹挟空气是引起该桥水毁破坏或加速该桥破坏的重要原因.
-
图 4 有限元和试验结果载荷-位移曲线对比
Figure 4. Comparison of load-displacement curves between FE and test results
表 1 CHS参数
Table 1. CHS parameters
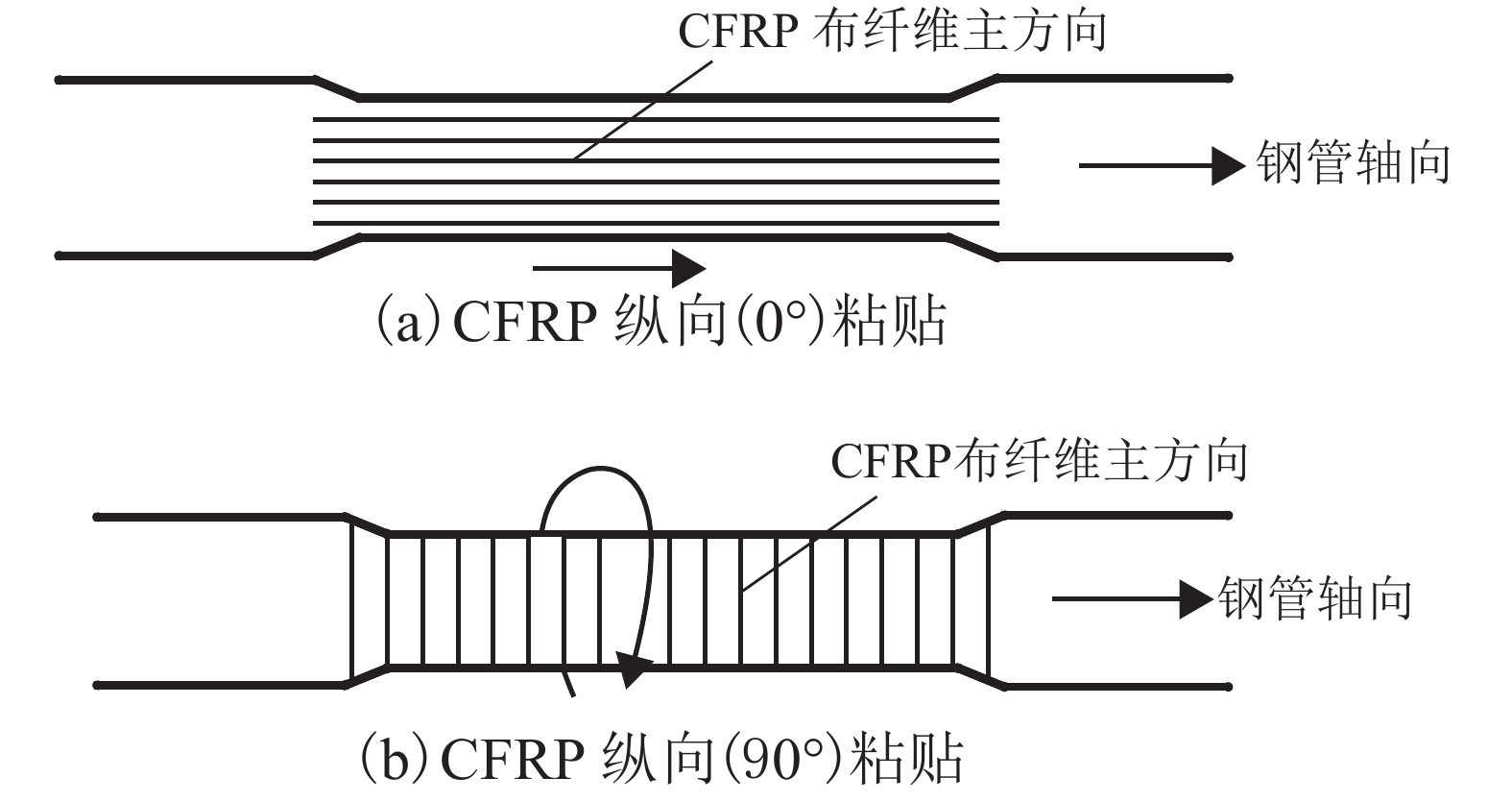
组号 试件编号 ${D_{\rm{s}}}$/mm ${t_{\rm{s}}}$/mm ${E_{\rm{s}}}$/（N•mm−2） $\sigma _{\rm{y}}$/（N•mm−2） ${E_{\rm{p,CFRP}}}$/（N•mm−2） ${D_{\rm{s}}}/{t_{\rm{s}}}$ $L/{D_{\rm{s}}}$ FRP 层数和方向 1 C-1 87.25 2.36 209 571 455 — 37 3.2 — CF-1A 87.23 2.32 209 571 455 230 000 38 3.2 1H1L CF-1B 87.21 2.32 209 571 455 230 000 38 3.2 2H2L 2 C-2 86.31 2.00 209 571 455 — 43 3.2 — CF-2A 86.38 1.91 209 571 455 230 000 45 3.2 1L1H CF-2B 86.39 1.96 209 571 455 230 000 44 3.2 2L2H 3 C-3 85.75 1.57 209 571 455 — 55 3.2 — CF-3A 85.68 1.57 209 571 455 230 000 54 3.2 1H1L 4 C-4 85.11 1.13 209 571 455 — 75 3.2 — CF-4A 85.21 1.10 209 571 455 230 000 78 3.2 1H1L 5 ST1 165 4.2 206 000 339 — 39 2.7 — ST2 166 4.2 206 000 339 76 000 40 2.7 1H ST3 165 4.2 206 000 339 76 000 39 2.7 2H ST4 165 4.2 206 000 339 76 000 39 2.7 2H 
下载: 导出CSV
表 2 CFRP材料属性
Table 2. CFRP material properties
${E_1}$/MPa ${E_2}$/MPa ${N_{\rm{u}}}$ ${G_{12}}$/MPa ${G_{13}}$/MPa ${G_{23}}$/MPa $t_{\rm{CFRP}}$/mm 230 000 1 900 0.3 3 387 3 387 3 387 0.176 注：当采用 文献[12 ]的模型建模时 $t_{\rm{CFRP}} = 0.17\;{\rm{mm}}$；E1 为纤维方向的弹性模量；E2 为垂直于纤维方向的弹性模量；
Nu 为泊松比；G12、G13、G23 为材料各平面内剪切模量.
下载: 导出CSV
表 3 Hashin失效参数
Table 3. Hashin’s failure parameters
MPa 方向 参数 值 方向 参数 值 X 拉伸强度 XT 1 830 Y 拉伸强度 YT 31.3 压缩强度 XC 895 压缩强度 YC 124.5 剪切强度 SL 72 剪切强度 ST 62.3
下载: 导出CSV
表 4 极限承载力对比分析
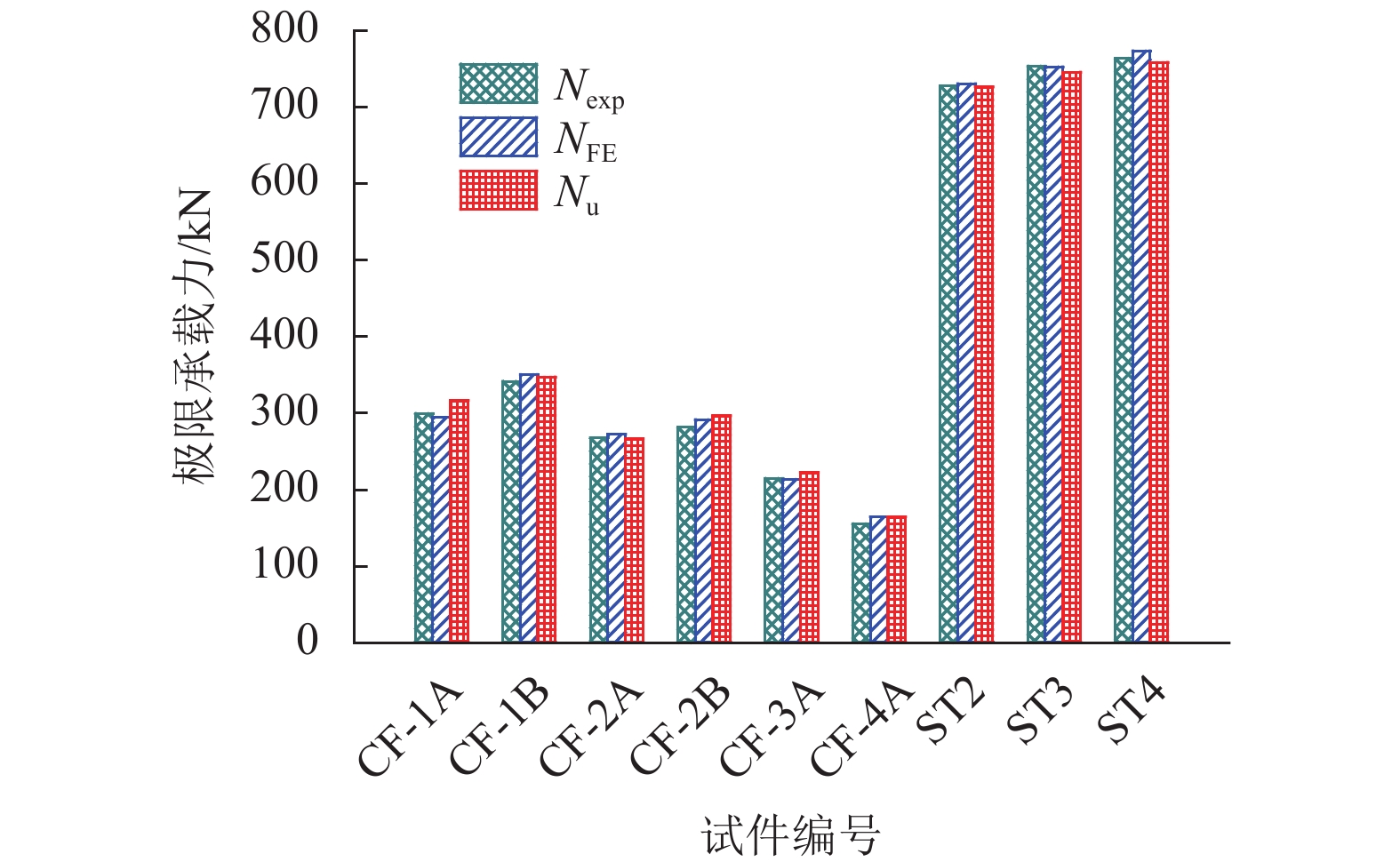
Table 4. Comparison and analysis of load carrying capacity
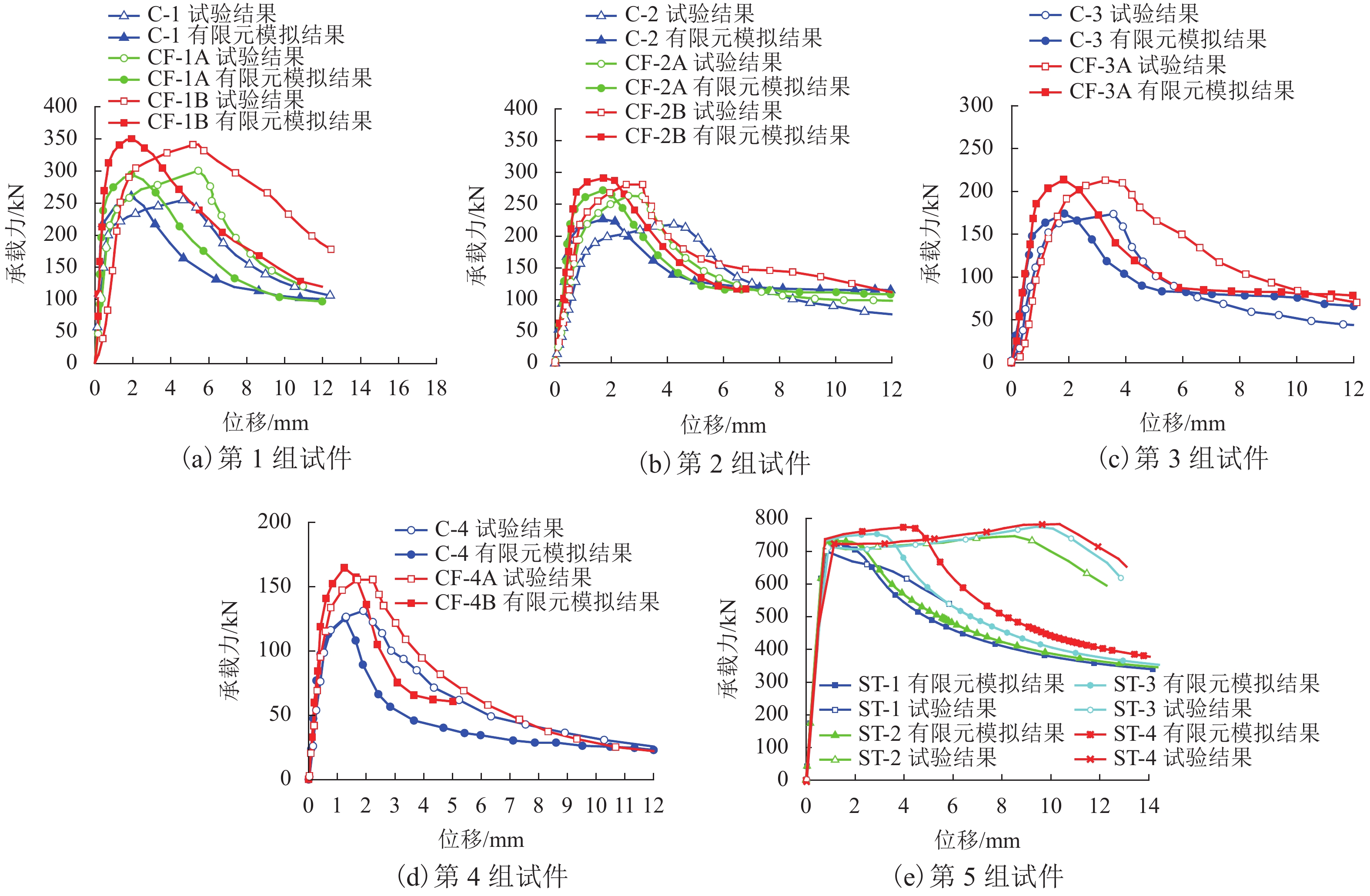
组 试件编号 Nexp/kN NFE/kN Nu/kN 提高率/% NFE/Nexp Nu/Nexp Nu/NFE 1 C-1 253 260 280 — 1.03 1.10 1.08 CF-1A 299 294 316 13 0.98 1.06 1.07 CF-1B 341 350 347 24 1.03 1.02 0.99 2 C-2 220 226 241 — 1.03 1.10 1.07 CF-2A 267 272 266 10.4 1.02 1.00 0.98 CF-2B 281 291 296 23 1.04 1.05 1.02 3 C-3 170 174 188 — 1.02 1.10 1.08 CF-3A 214 213 222 22.4 1.00 1.04 1.04 4 C-4 120 125 137 — 1.04 1.14 1.10 CF-4A 155 164 164 31.2 1.06 1.06 1.00 5 ST1 719 722 719 — 1.00 1.00 1.00 ST2 727 730 726 1.4 1.00 1.00 0.99 ST3 753 752 745 4.7 1.00 0.99 0.99 ST4 763 763 758 6.2 1.00 0.99 0.99
下载: 导出CSV
-
季园园,韩庆华,芦燕,等. CFRP在土木工程中的应用研究[J]. 结构工程师,2014(5): 210-219. doi: 10.3969/j.issn.1005-0159.2014.05.032JI Yuanyuan, HAN Qinghua, LU Yan, et al. Application research of CFRP in civil engineering[J]. Structural Engineers, 2014(5): 210-219. doi: 10.3969/j.issn.1005-0159.2014.05.032 SEICA M V, PACKER J A. FRP materials for the rehabilitation of tubular steel structures for underwater applications[J]. Composite Structures, 2007, 80(3): 440-450. doi: 10.1016/j.compstruct.2006.05.029 完海鹰,江勇. 碳纤维复材布加固轴压圆管柱静力试验和数值分析[J]. 工业建筑,2017,47(2): 33-37.WAN Haiying, JIANG Yong. A static test and numerical analysis of circular hollow section (CHS) columns reinforced by CFRP sheets under axial compression[J]. Industrial Construction, 2017, 47(2): 33-37. 朱佳,完海鹰. 碳纤维增强复合材料加固轴压足尺圆管柱的试验研究[J]. 工业建筑,2016,46(4): 104-109.ZHU Jia, WAN Haiying. Experimental study of full scale circular hollow section (CHS) columns reinforced by CFRP under axial compression[J]. Industrial Construction, 2016, 46(4): 104-109. 周乐,王晓初,王军伟,等. 负载条件下CFRP加固轴心受压钢管短柱受力性能研究[J]. 工程力学,2015,32(11): 201-209. doi: 10.6052/j.issn.1000-4750.2014.04.0357ZHOU Le, WANG Xiaochu, WANG Junwei, et al. Research on mechanical properties of axially loaded tubular steel stub columns reinforced by CFRP[J]. Engineering Mechanics, 2015, 32(11): 201-209. doi: 10.6052/j.issn.1000-4750.2014.04.0357 李兆阳,高小育,陈沿辰. 碳纤维布加固钢管轴压短柱有限元分析[J]. 四川理工学院学报(自然科学版),2015,28(5): 74-80. doi: 10.11863/j.suse.2015.05.14LI Zhaoyang, GAO Xiaoyu, CHEN Yanchen. Finite element analysis of CFRP strengthened steel tubular short columns under axial compression[J]. Journal of Sichuan University of Science & Engineering (Natural Science Edition), 2015, 28(5): 74-80. doi: 10.11863/j.suse.2015.05.14 南波, 武岳,孙浩田. 缠绕型CFRP圆管轴压力学性能[J]. 工程力学,2017,34(1): 92-100.NAN Bo, WU Yue, SUN Haotian. Mechanical properties of filament-wound CFRP tube under axially compressive load[J]. Engineering Mechanics, 2017, 34(1): 92-100. 南波,武岳,孙浩田. 拉挤型CFRP管轴压性能[J]. 哈尔滨工程大学学报,2015,36(6): 779-783.NAN Bo, WU Yue, SUN Haotian. Buckling behavior of pultruded carbon fiber reinforced polymer under axially compressive load[J]. Journal of Harbin Engineering University, 2015, 36(6): 779-783. 张贵文,李俊杰,王秀丽. 碳纤维布加固薄壁圆钢管轴心抗拉承载力有限元分析[J]. 甘肃科学学报,2012,24(1): 32-36. doi: 10.3969/j.issn.1004-0366.2012.01.009ZHANG Guiwen, LI Junjie, WANG Xiuli. Finite element analysis on axial tensile bearing capacity of round thin-walled steel-tubes strengthened with CFRP sheets[J]. Journal of Gansu Sciences, 2012, 24(1): 32-36. doi: 10.3969/j.issn.1004-0366.2012.01.009 HAEDIR J, ZHAO X L, BANBACH M R, et al. Analysis of CFRP externally-reinforced steel CHS tubular beams[J]. Composite Structures, 2010, 92(12): 2992-3001. doi: 10.1016/j.compstruct.2010.05.012 HAEDIR J, ZHAO X L. Design of short CFRP-reinforced steel tubular columns[J]. Journal of Constructional Steel Research, 2011, 67(3): 497-509. doi: 10.1016/j.jcsr.2010.09.005 TENG J G, HU Y M. Behavior of FRP-jacketed circular steel tubes and cylindrical shells under axial compression[J]. Construction & Building Materials, 2007, 21(4): 827-838. 刘勇,陈世健,高鑫,等. 基于Hashin准则的单层板渐进失效分析[J]. 装备环境工程,2010,7(1): 34-39. doi: 10.3969/j.issn.1672-9242.2010.01.009LIU Yong, CHEN Shijian, GAO Xin, et al. Progressive failure analysis of monolayer composite based on Hashin criterion[J]. Equipment Environmental Engineering, 2010, 7(1): 34-39. doi: 10.3969/j.issn.1672-9242.2010.01.009 庄茁. ABAQUS非线性有限元分析与实例[M]. 北京: 科学出版社, 2005: 55-90. 廖云龙,吴剑. 基于Riks方法的复合材料贮箱稳定性分析[J]. 火箭推进,2013,39(5): 65-69. doi: 10.3969/j.issn.1672-9374.2013.05.012LIAO Yunlong, WU Jian. Stability analysis based on Riks method for composite material vessel[J]. Journal of Rocket Propulsion, 2013, 39(5): 65-69. doi: 10.3969/j.issn.1672-9374.2013.05.012 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 558
- HTML全文浏览量: 269
- PDF下载量: 11
- 被引次数: 0
