Traction Load Classification Method Based on Improved Clustering Method
-
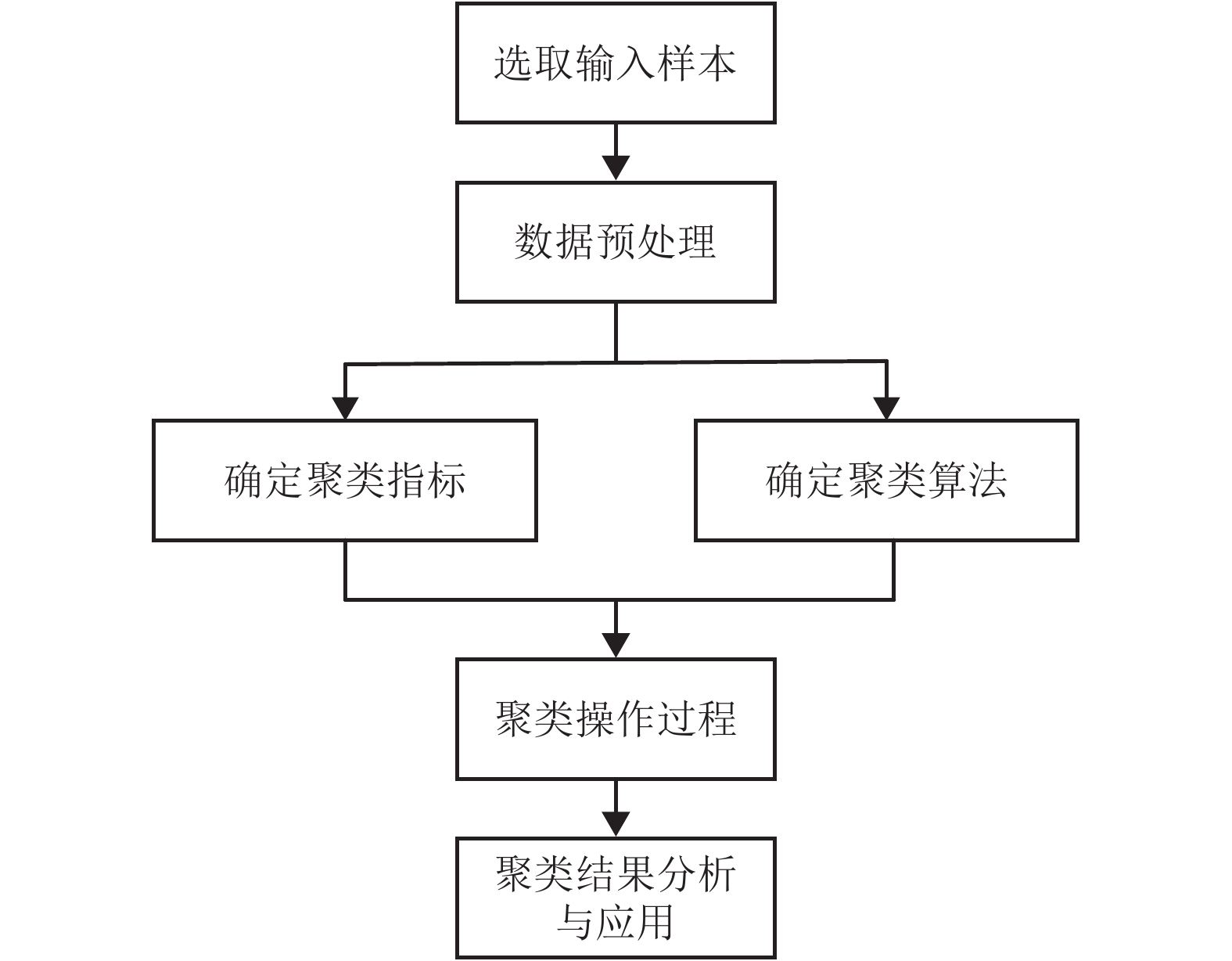
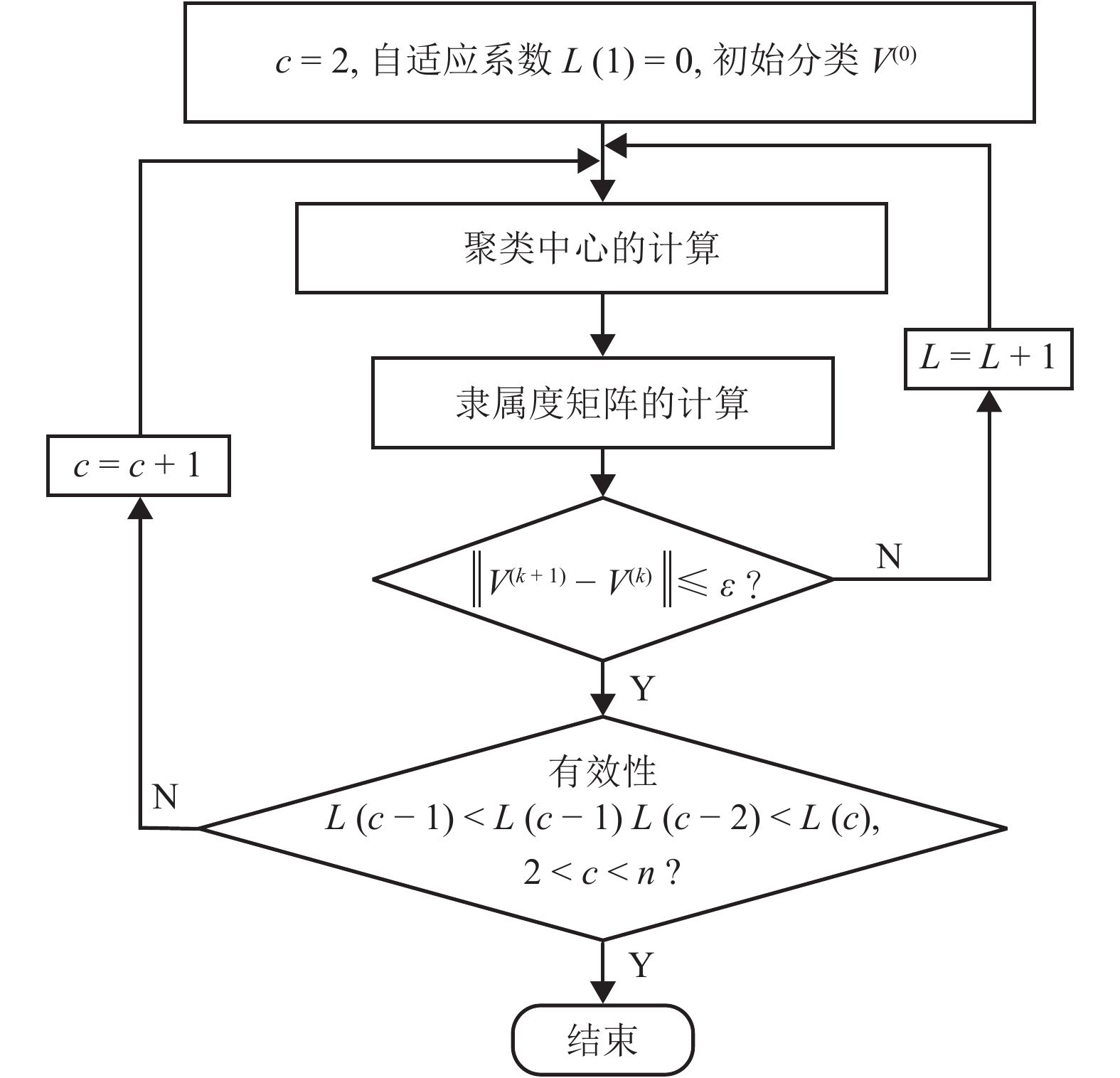
摘要: 为得到更为准确的牵引负荷分类结果，基于大量的牵引负荷实测数据，提出了一种改进后的自适应模糊C均值聚类方法. 该方法能够自动获取最佳聚类数，以馈线电流带电有效系数、最大值、平均值、95%值以及1～5阶样本矩作为聚类指标对实测牵引负荷进行聚类；然后采用非参数核密度估计方法对牵引负荷概率密度函数进行拟合，得到了每一类馈线电流概率分布模型. 结果表明：聚为一类的牵引负荷特征参数相近、概率分布相似.Abstract: In order to obtain more accurate traction load classification, based on a large amount of measured traction load data, an improved fuzzy C-means clustering method is proposed, which can automatically obtain the best classification number. A charged effective coefficient, the maximum value, the average value, the value of 95% and one to five order moments were chosen as clustering indicators to classify feeder current. Then the probability density function of traction loads was fitted using non-parametric kernel density estimation, and the probability distribution model of each feeder current type was obtained. The results show that the characteristic parameters and probability distributions of the traction loads that were clustered together are.
-
图 4 馈线电流的概率密度函数拟合曲线
Figure 4. Probability density function fitting curve of feeder current
表 1 特征参数的权重分配
Table 1. Weight distribution of characteristic parameters
参数 权重 参数 权重 偏度 0.5 一阶矩 0.8 峰度 0.5 二阶矩 0.8 带电有效系数 0.8 三阶矩 0.1 Imax/Imean 0.8 四阶矩 0.1 I95/Imean 0.5 五阶矩 0.1 Iyou/Imean 0.1 空载系数 0.5 
下载: 导出CSV
表 2 馈线电流的隶属度
Table 2. Feeder current membership
样本 第 Ⅰ 类 第 2 类 第 3 类 第 4 类 第 5 类 第 6 类 样本 第 Ⅰ 类 第 2 类 第 3 类 第 4 类 第 5 类 第 6 类 负荷1 0.169 0.217 0.108 0.255 0.151 0.100 负荷17 0.076 0.093 0.224 0.138 0.115 0.355 负荷2 0.517 0.185 0.053 0.109 0.087 0.050 负荷18 0.074 0.089 0.152 0.113 0.098 0.473 负荷3 0.407 0.207 0.066 0.142 0.117 0.060 负荷19 0.126 0.204 0.106 0.295 0.139 0.129 负荷4 0.077 0.086 0.445 0.121 0.135 0.137 负荷20 0.093 0.118 0.155 0.269 0.251 0.114 负荷5 0.103 0.119 0.249 0.156 0.137 0.237 负荷21 0.167 0.268 0.096 0.221 0.135 0.113 负荷6 0.040 0.047 0.679 0.069 0.074 0.092 负荷22 0.040 0.061 0.031 0.787 0.054 0.028 负荷7 0.362 0.266 0.067 0.137 0.102 0.066 负荷23 0.131 0.142 0.103 0.213 0.334 0.077 负荷8 0.107 0.124 0.182 0.144 0.128 0.315 负荷24 0.128 0.135 0.170 0.186 0.277 0.105 负荷9 0.268 0.336 0.072 0.147 0.101 0.077 负荷25 0.013 0.015 0.016 0.025 0.920 0.011 负荷10 0.211 0.283 0.090 0.198 0.129 0.090 负荷26 0.105 0.110 0.100 0.157 0.456 0.072 负荷11 0.193 0.408 0.065 0.167 0.096 0.071 负荷27 0.101 0.105 0.115 0.151 0.450 0.077 负荷12 0.449 0.192 0.066 0.124 0.108 0.061 负荷28 0.152 0.164 0.094 0.219 0.293 0.077 负荷13 0.327 0.340 0.057 0.131 0.089 0.057 负荷29 0.081 0.090 0.402 0.133 0.173 0.120 负荷14 0.612 0.164 0.040 0.083 0.063 0.039 负荷30 0.096 0.105 0.165 0.160 0.378 0.097 负荷15 0.048 0.060 0.095 0.081 0.064 0.653 负荷31 0.068 0.078 0.472 0.116 0.147 0.119 负荷16 0.100 0.131 0.166 0.199 0.141 0.263
下载: 导出CSV
表 3 3类牵引负荷的特征值
Table 3. Characteristic values of three types of traction loads
分类 偏度 峰度 Imax/Imean I95/Imean 带电有效系数 空载概率 1-1 1.36 5.12 5.20 2.45 1.20 0.47 1-2 1.56 6.81 6.16 2.45 1.23 0.35 1-3 1.46 5.63 5.52 2.51 1.24 0.25 1-4 1.06 4.48 6.78 2.35 1.11 0.68 2-1 0.65 3.29 3.47 2.23 1.05 0.73 2-2 0.70 3.34 3.97 1.88 1.08 0.69 2-3 0.85 4.28 5.30 2.12 1.02 0.65 2-4 0.50 3.58 3.28 1.89 1.05 0.70 2-5 0.75 3.85 4.34 2.14 1.06 0.68 3-1 2.43 10.92 11.98 3.35 1.50 0.31 3-2 2.13 9.05 8.20 3.09 1.34 0.30 3-3 1.67 5.64 6.83 3.12 1.35 0.32 3-4 2.03 7.61 7.73 3.19 1.31 0.38 3-5 2.13 9.13 10.10 3.24 1.38 0.17 注：表中所有数据处理时均采用电流即时值比电流最大值.
下载: 导出CSV
-
李群湛. 电气化铁道并联综合补偿及其应用[M]. 北京: 中国铁道出版社, 1993: 10-46. 刘思,傅旭华,叶承晋,等. 应用聚类分析与非参数核密度估计的空间负荷分布规律[J]. 电网技术,2017,41(2): 604-610.LIU Si, FU Xunhua, YE Chengjin, et al. Spatial load distribution based on clustering analysis and non-parametric kernel density estimation[J]. Power System Technology, 2017, 41(2): 604-610. 张斌,庄池杰,胡军,等. 结合降维技术的电力负荷曲线集成聚类算法[J]. 中国电机工程学报,2015,35(15): 3741-3749.ZHANG Bin, ZHUANG Chijie, HU Jun, et al. Ensemble clustering algorithm combined with dimension reduction techniques for power load profiles[J]. Proceedings of the CSEE, 2015, 35(15): 3741-3749. 林顺富,田二伟,符杨,等. 基于信息熵分段聚合近似和谱聚类的负荷分类方法[J]. 中国电机工程学报,2017,37(8): 2242-2253.LIN Shunfu, TIAN Erwei, FU Yang, et al. Power load classification method based on information entropy piecewise aggregate approximation and spectral clustering[J]. Proceedings of the CSEE, 2017, 37(8): 2242-2253. 苏学能,刘天琪,曹鸿谦,等. 基于Hadoop架构的多重分布式BP神经网络的短期负荷预测方法[J]. 中国电机工程学报,2017,37(17): 4966-4973,5216.SU Xueneng, LIU Tianqi, CAO Hongqian, et al. A multiple distributed bp neural networks approach for short-term load forecasting based on Hadoop framework[J]. Proceedings of the CSEE, 2017, 37(17): 4966-4973,5216. 沈沉,秦建,盛万兴,等. 基于小波聚类的配变短期负荷预测方法研究[J]. 电网技术,2016,40(2): 521-526.SHEN Chen, QIN Jian, SHENG Wanxing, et al. Study on short-term forecasting of distribution transformer load using wavelet and clustering method[J]. Power System Technology, 2016, 40(2): 521-526. 张丽艳,李群湛,朱毅. 新建电气化铁路牵引负荷预测[J]. 西南交通大学学报,2016,51(4): 743-749. doi: 10.3969/j.issn.0258-2724.2016.04.020ZHANG Liyan, LI Qunzhan, ZHU Yi. Prediction of traction load for new electrified railway[J]. Journal of Southwest Jiaotong University, 2016, 51(4): 743-749. doi: 10.3969/j.issn.0258-2724.2016.04.020 石若颖. 新建电气化铁路牵引负荷统计预测研究[D]. 成都: 西南交通大学, 2017. 陈玉祥, 张汉亚. 预测技术与应用[M]. 北京: 机械工业出版社, 1985: 98-109. 陈立周, 何晓峰, 翁海珊. 工程随机变量优化方法设计原理与应用[M]. 北京: 科学出版社, 1997: 45-67. 杨浩,张磊,何潜,等. 基于自适应模糊C均值算法的电力负荷分类研究[J]. 电力系统保护与控制,2010,38(16): 111-115,122. doi: 10.7667/j.issn.1674-3415.2010.16.022YANG Hao, ZHANG Lei, HE Qian, et al. Study of power load classification based on adaptive fuzzy C means[J]. Power System Protection and Control, 2010, 38(16): 111-115,122. doi: 10.7667/j.issn.1674-3415.2010.16.022 许国根, 贾瑛著. 实战大数据——MATLAB数据挖掘详解与实践[M]. 清华大学出版社, 2017: 57-78. 张丽艳,李群湛,解绍锋. 牵引变电所馈线电流的概率模型[J]. 西南交通大学学报,2009,42(6): 848-854. doi: 10.3969/j.issn.0258-2724.2009.06.009ZHANG Liyan, LI Qunzhan, XIE Shaofeng. Probability distribution of feeder current of traction substation[J]. Journal of Southwest Jiaotong University, 2009, 42(6): 848-854. doi: 10.3969/j.issn.0258-2724.2009.06.009 周开乐,杨善林. 基于改进模糊C均值算法的电力负荷特性分类[J]. 电力系统保护与控制,2012,40(22): 58-63. doi: 10.7667/j.issn.1674-3415.2012.22.010ZHOU Kaile, YANG Shanlin. An improved fuzzy C-means algorithm for power load characteristics classification[J]. Power System Protection and Control, 2012, 40(22): 58-63. doi: 10.7667/j.issn.1674-3415.2012.22.010 何友全,肖建,方磊. 数据挖掘技术及在铁道牵引供电系统中的应用[J]. 电气化铁道,2003(4): 5-8.HE Youquan, XIAO Jian, FANG Lei. Data mining technology and its application in railway traction power supply system[J]. Electric Railway, 2003(4): 5-8. 解绍锋,李群湛,赵丽平. 电气化铁道牵引负载谐波分布特征与概率模型研究[J]. 中国电机工程学报,2005,25(16): 79-83. doi: 10.3321/j.issn:0258-8013.2005.16.015XIE Shaofeng, LI Qunzhan, ZHAO Liping. Study on harmonic distribution characteristic and probability model of the traction load of electrified railway[J]. Proceedings of the CSEE, 2005, 25(16): 79-83. doi: 10.3321/j.issn:0258-8013.2005.16.015 陈民武,刘洋,韩旭东. 高速铁路牵引负荷谐波分布的非参数估计模型与预测评估研究[J]. 电网技术,2017,41(8): 2598-2603.CHEN Minwu, WU Yang, HAN Xudong. Harmonic prediction evaluation for high speed railway traction load[J]. Power System Technology, 2017, 41(8): 2598-2603. YUEN K H, YE Z M, PONG M H, et al. Modeling of traction harmonic current using statistical method[C]// Proceedings of the IEEE 1999 International Conference. [S.l.]: IEEE, 1999: 194-199. CHICCO G. Overview and performance assessment of the clustering methods for electrical load pattern grouping[J]. Energy, 2012, 42(1): 68-80. doi: 10.1016/j.energy.2011.12.031 廖志伟,孙雅明. 数据挖掘技术及其在电力系统中的应用[J]. 电力系统自动化,2001,25(11): 62-66. doi: 10.3321/j.issn:1000-1026.2001.11.017LIAO Zhiwei, SUN Yaming. Data mining technology and its application in power system[J]. Automation of Electric Power Systems, 2001, 25(11): 62-66. doi: 10.3321/j.issn:1000-1026.2001.11.017 PRAHASTONO I, KING D J, OZVEREN C S, et al. Electricity load profile classification using fuzzy C-means method[C]//The 43rd International Universities Power Engineering Conference, UPEC 2008. [S.l.]: IEEE, 2008: 1-5. DONG H B, DONG Y X, ZHOU C, et al. A fuzzy clustering algorithm based on evolutionary programming[J]. Expert Systems with Applications, 2009, 36(9): 11792-11800. doi: 10.1016/j.eswa.2009.04.031 BAI Liyuan, HU Shengyan, LIU Suhua. A fuzzy clustering algorithm based on simulated annealing and genetic algorithm[J]. Computer Engineering and Application, 2005, 9(36): 56-57. XIE X L, BENI G A. Validity measure for fuzzy clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(8): 841-847. doi: 10.1109/34.85677 -
下载:
点击查看大图
图(4) / 表(3)
计量
- 文章访问数: 520
- HTML全文浏览量: 212
- PDF下载量: 8
- 被引次数: 0