Assembly Accuracy Analysis of Small Deformation of Flexible Body based on Differential Transformation
-
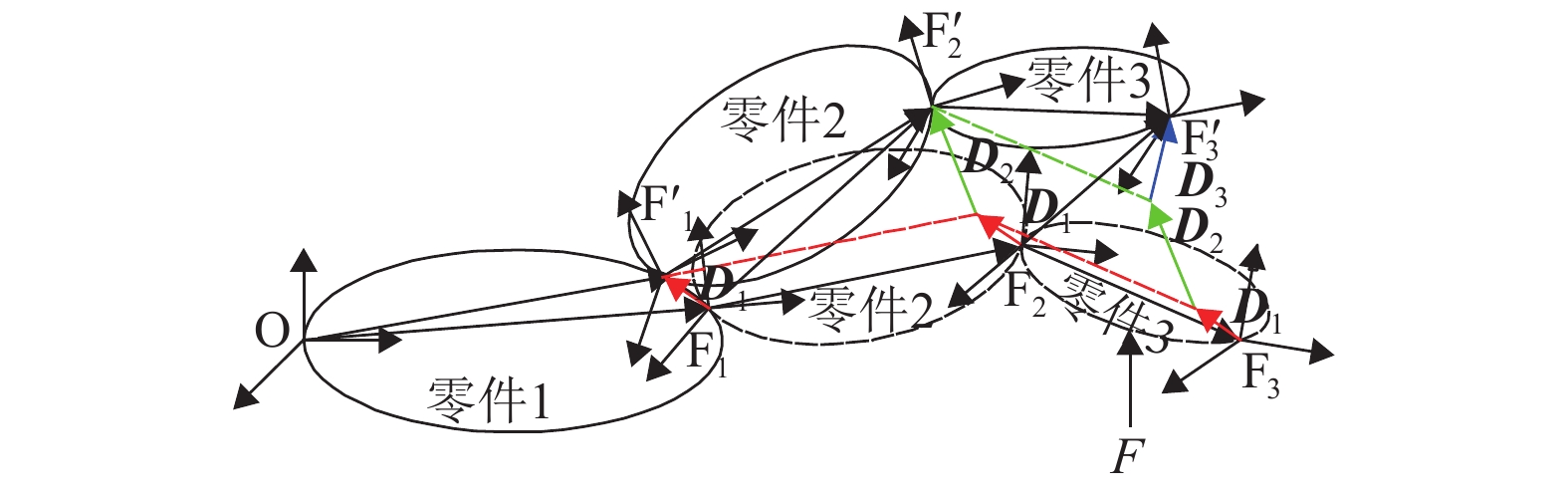
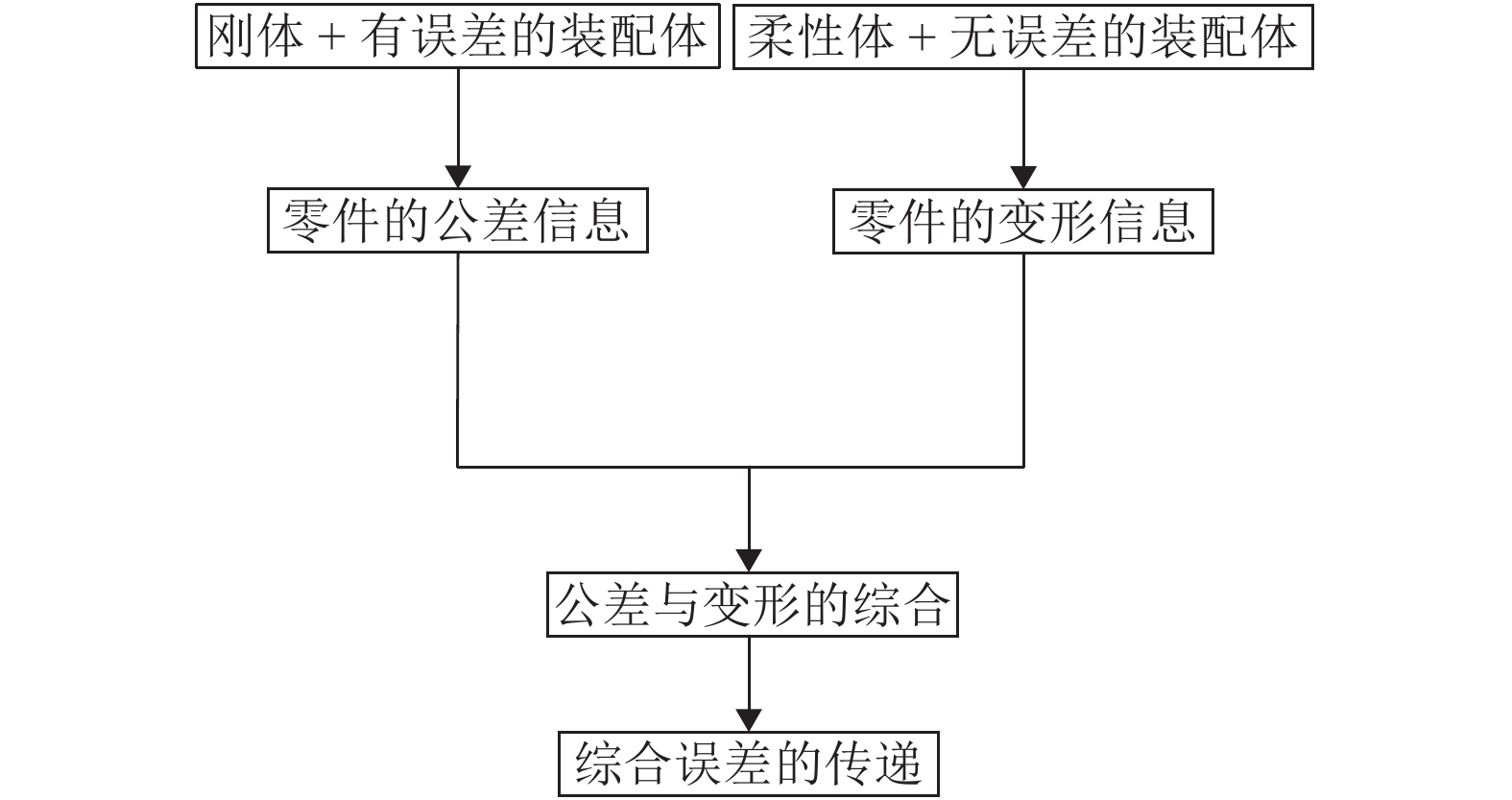
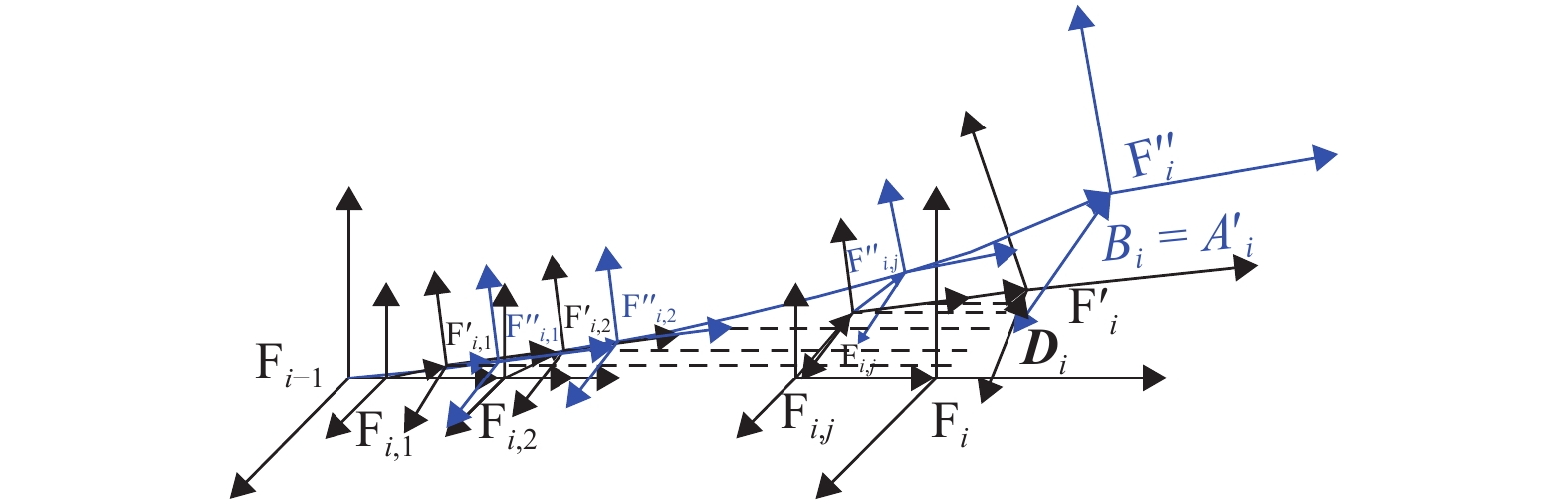
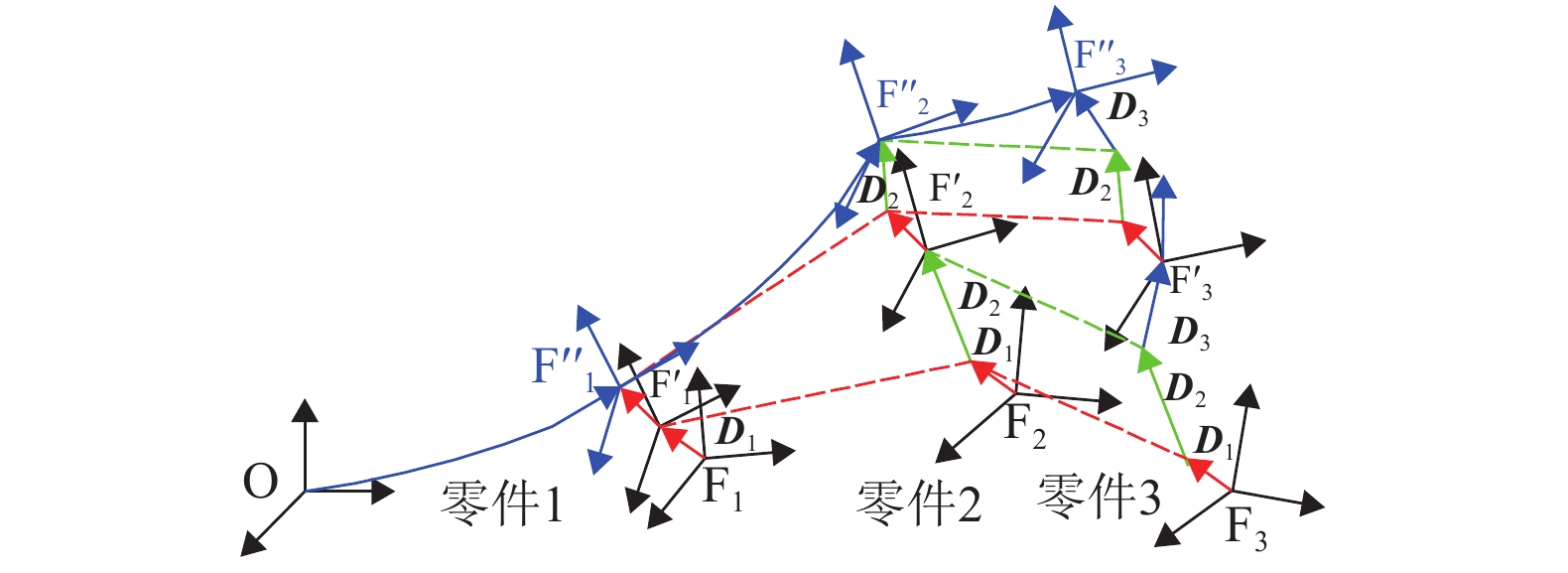
摘要: 在产品设计阶段进行装配精度分析时通常以刚体假设为前提，往往忽略外部载荷、温度变化等载荷因素的影响. 在已存在制造误差、装配误差的情况下，载荷因素引起的零件变形会进一步影响装配精度. 因此，本文提出了一种同时考虑制造、装配误差和零件变形的装配精度分析模型. 该模型首先沿尺寸链将变形的公差特征离散化，在每个节点处建立并固结节点坐标系；然后提取节点的变形信息，对目标特征上的每个节点坐标系进行微分变换，实现误差与变形的综合；最后建立了线性化的综合误差分析模型. 研究结果表明：模型不仅克服了传统误差分析模型以刚体假设为前提的局限，得到了零件的局部变形对装配精度的影响，还可极大地减少装配系统几何建模与力学分析的难度和工作量.Abstract: Rigid body assumptions were usually used as the premise for assembly accuracy analysis during the product design stage, and the effects of load factors such as external loads and temperature changes were often ignored. In the case of manufacturing errors and assembly errors, the deformation of the part caused by the load factor would further affect the assembly accuracy. Therefore, an assembly accuracy analysis model that considered manufacturing , assembly errors, and part deformations simultaneously was proposed. Firstly, the model made the deformed Tolerance Features discretized along the dimensional chain, and established and consolidated the node coordinate system at each node. Then, the node's deformation information was extracted and differential transformation on each node coordinate system on the target feature was performed to achieve the error synthesis with deformation. Finally, a linearized comprehensive error analysis model was established. The results show that the model overcomes the limitations of the traditional error analysis model based on the assumption of rigid bodies, obtains the effect of the local deformation of parts on assembly accuracy, and also greatly reduce the difficulties and workload of geometric modeling and mechanical analysis.
-
Key words:
- error analysis /
- small deformation /
- differential transformation /
- product design
-
图 1 TF上的局部坐标系和节点坐标系
Figure 1. Local coordinate systems and node coordinate systems on TF
图 5 3种不同类型坐标系构成的尺寸链
Figure 5. Dimensional chain of three different types of coordinate systems
图 7 齿轮轴线端点变动凸包的形状与位置
Figure 7. Shape and position of convex hulls of the end point of gear shaft
表 1 齿轮轴线端点处的变形值
Table 1. Deformation value of the gear axis end
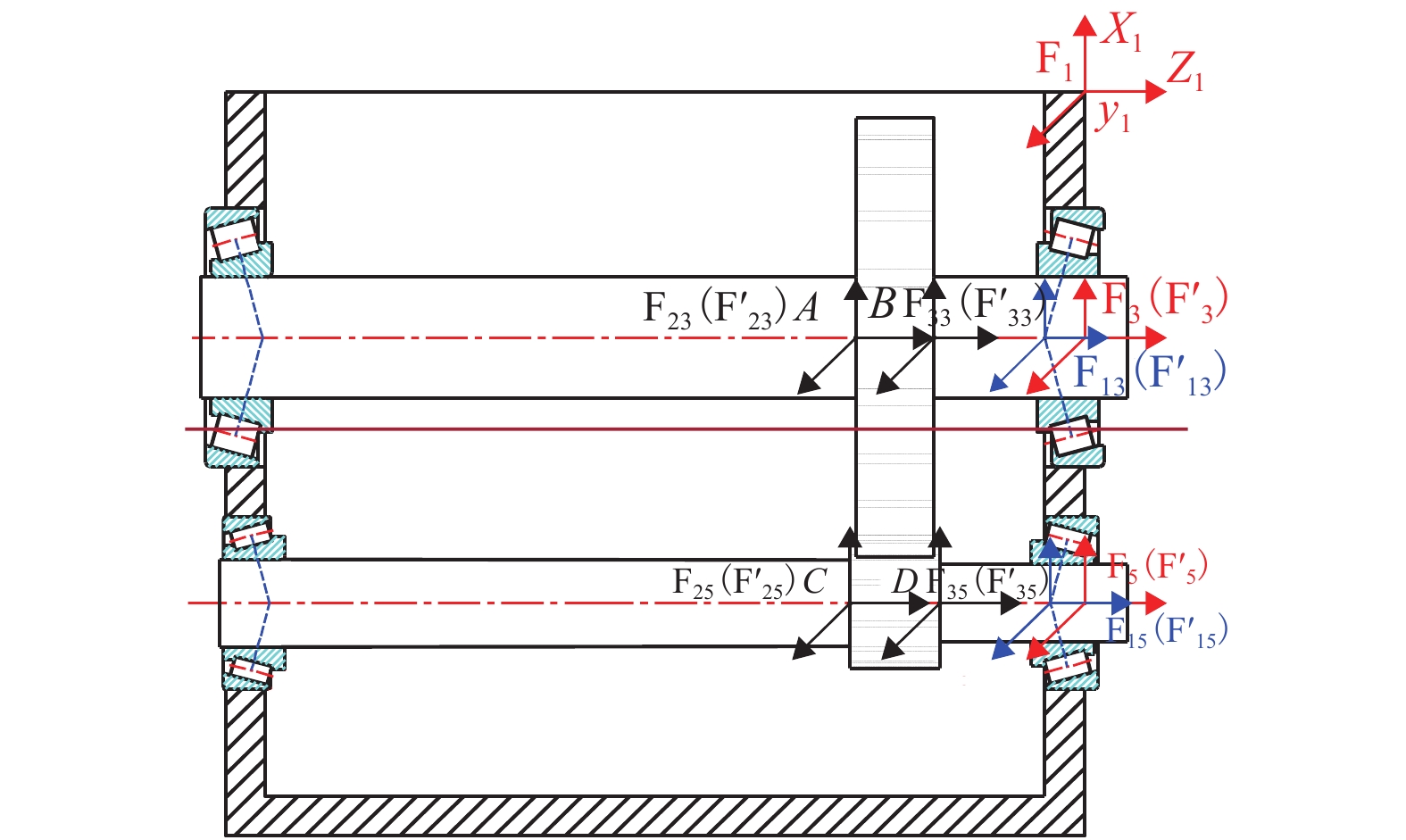
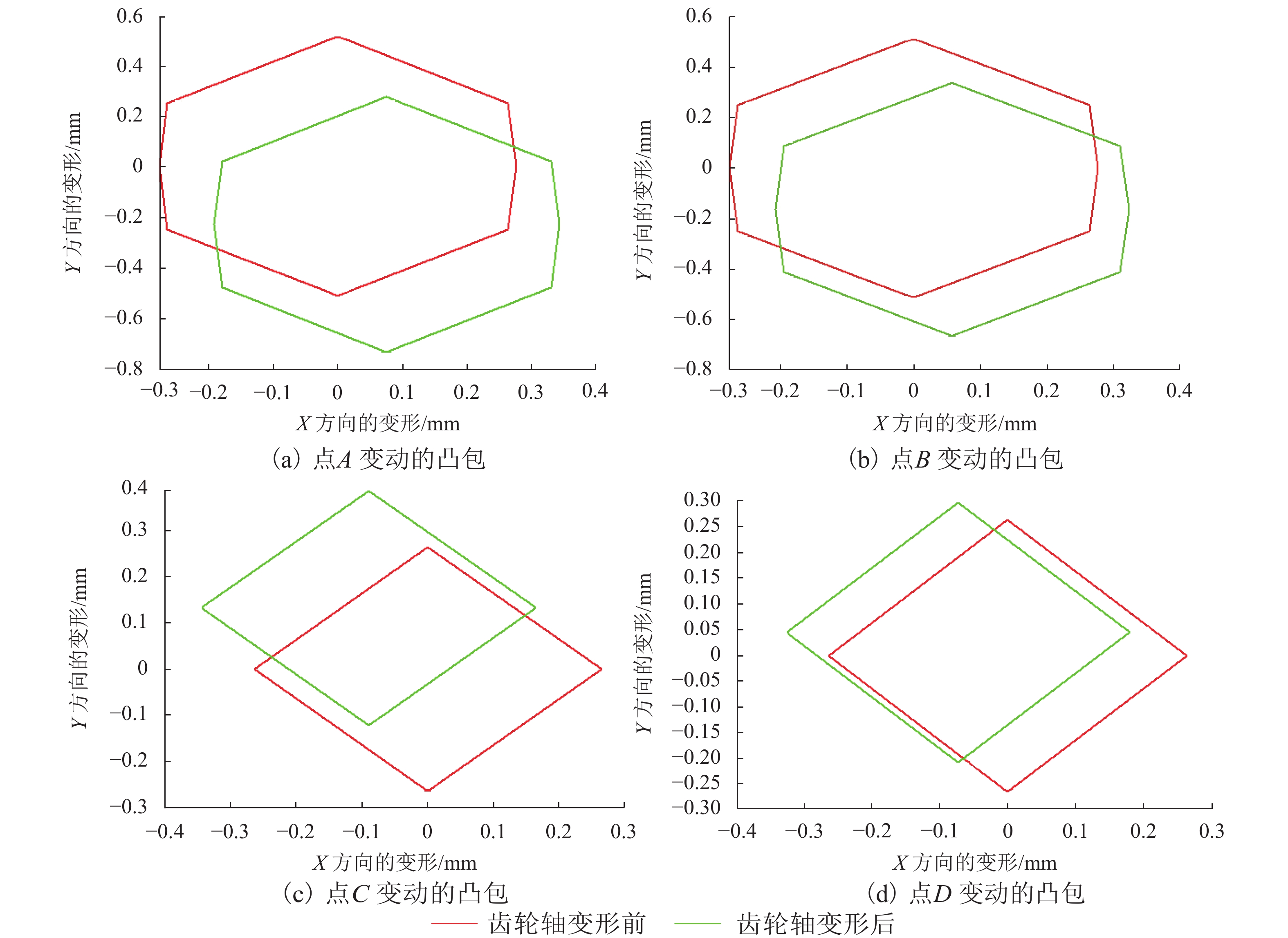
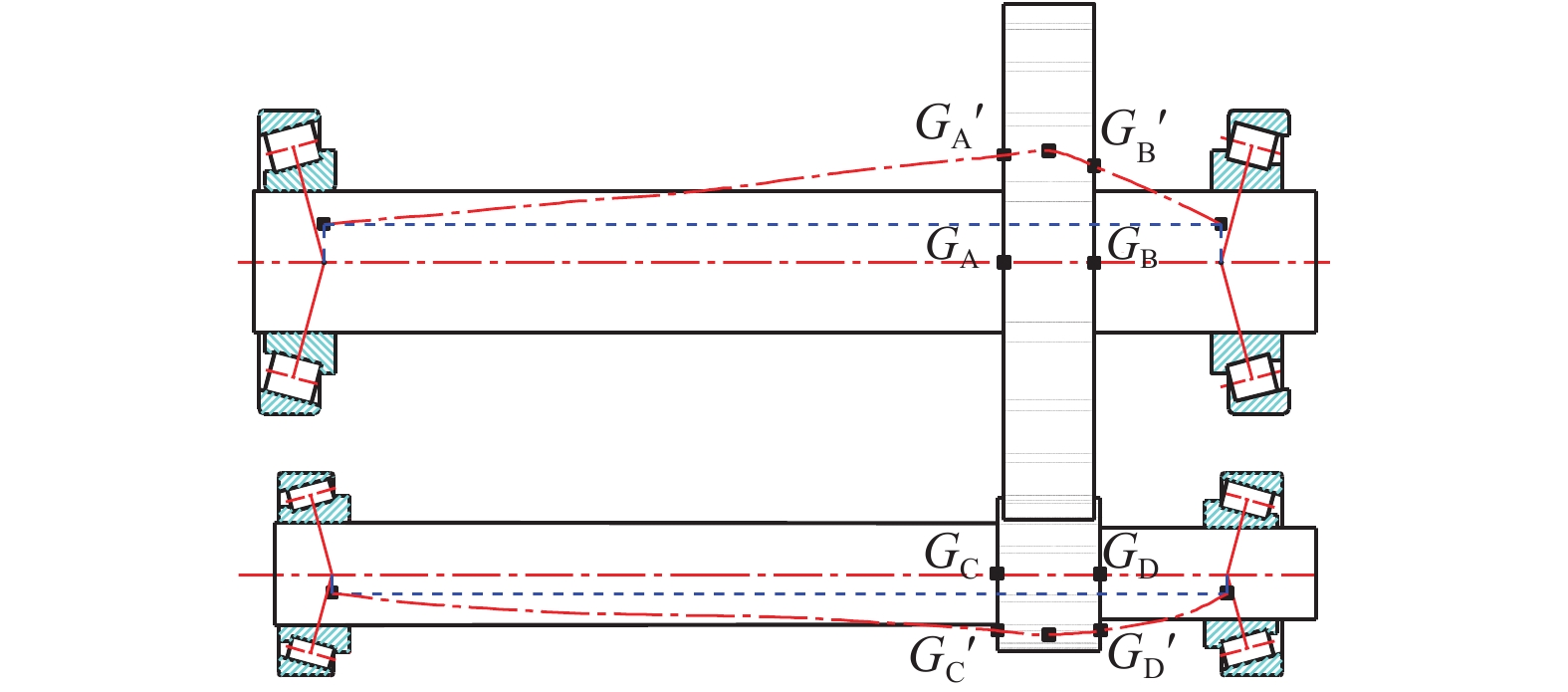
端点 输出轴的变形/mm 端点 中间轴的变形/mm X13 方向 Y13 方向 X15 方向 Y15 方向 A 0.07562 −0.2311 C −0.08983 0.13210 B 0.05764 −0.1631 D −0.07237 0.04538 
下载: 导出CSV
-
刘建永,乔立红. 一种考虑零件变形的装配误差计算方法[J]. 计算机集成制造系统,2015,21(1): 94-100.LIU Jianyong, QIAO Lihong. Calculation method for assembly error with consideration of part deformation[J]. Computer Integrated Manufacturing Systems, 2015, 21(1): 94-100. 罗少敏,徐诚. 考虑变形影响的公差分析及其研究进展[J]. 机械工程学报,2016,7(1): 139-151.LUO Shaomin, XU Cheng. Research progress of tolerance analysis taking into account the deformation[J]. Journal of Mechanical Engineering, 2016, 7(1): 139-151. GILBERT O L Representation of geometric variations using matrix transforms for statistical tolerance ananlysis in assemblies[D]. [S.l.]: Massachusetts Institute of Technology, 1988. WHITNEY D E, GILBERT O L, JASTRZEBSKI M. Representation of geometric variations using matrix transforms for statistical tolerance analysis in assemblies[J]. Research in Engineering Design, 1994, 16(4): 191-210. CHASE K W, MAGLEBY S P, GLANCY C G. A comprehensive system for computer-aided tolerance analysis of 2-D and 3-D mechanical assemblies[C]//Proceedings of the 5th International Seminar on Computer-Aided Tolerancing. Toronto: [s.n.] , 1997: 27-29. DESROCHERS A, GHIE W, LAPERRIERE L. Application of a unified Jacobian-Torsor model for tolerance analysis[J]. Journal of Computing and Information Science in Engineering, 2003, 3(1): 2-14. doi: 10.1115/1.1573235 BHIDE S, AMETA G, DAVIDSON J K, et al. Tolerance-maps applied to the straightness and orientation of an axis[M]. [S.l.]: Springer, 2007: 45-54 LIU S C, HU S J. Variation simulation for deformable sheet metal assemblies using finite element methods[J]. Journal of Manufacturing Science & Engineering, 1997, 119(3): 368-374. HU S J, KOREN Y. Stream-of-variation theory for automotive body assembly[J]. CIRP Annals - Manufacturing Technology, 1997, 46(1): 1-6. doi: 10.1016/S0007-8506(07)60763-X LIU S C, LEE H W, HU S J. Variation simulation for deformable sheet metal assemblies using mechanistic models[J]. Journal of Manufacturing Science & Engineering, 1997, 119(3): 368-374. LIU T, CAO Y, WANG J, et al. Assembly error calculation with consideration of part deformation[J]. Procedia Cirp, 2016, 43: 58-63. GUO J, LI B, LIU Z, et al. Integration of geometric variation and part deformation into variation propagation of 3-D assemblies[J]. International Journal of Production Research, 2016, 54(19): 1-14. SAMPER S, GIORDANO M. Taking into account elastic displacements in 3D tolerancing-models and application[J]. Journal of Materials Processing Technology, 1998, 78(1): 156-162. ZHONG W, HU S J. Modeling machining geometric variation in a N-2-1 fixturing scheme[J]. Journal of Manufacturing Science & Engineering, 2006, 128(1): 213-219. 张为民,陈灿,李鹏忠,等. 基于雅可比旋量法的实际工况公差建模[J]. 计算机集成制造系统,2011,17(1): 77-83.ZHANG Weimin, CHEN Can, LI Pengzhong, et al. Tolerance modeling in actual working condition based on Jacobian-Torsor theory[J]. Computer Integrated Manufacturing Systems, 2011, 17(1): 77-83. 冯䶮,洪军,郭俊康,等. 基于新一代产品几何技术规范的工作载荷下公差建模[J]. 计算机集成制造系统,2013,19(7): 1500-1508.FENG Yan, HONG Jun, GUO Junkang, et al. Tolerance modeling of working load based on geometrical product specifications[J]. Computer Integrated Manufacturing Systems, 2013, 19(7): 1500-1508. 赵强强,洪军,刘志刚, 等. 任意拓扑结构机床运动轴误差传递链建模方法[J]. 机械工程学报,2016,52(21): 130-137. doi: 10.3901/JME.2016.21.130ZHAO Qiangqiang, HONG Jun, LIU Zhigang, et al. Mo ling method on motive axes error transfer chain for machine tool of arbitrary topological structure [J]. Journal of Mechanical Engineering, 2016, 52(21): 130-137. doi: 10.3901/JME.2016.21.130 齐继宝,杨伟民. 基于微分变化构造法的数控机床几何误差补偿方法[J]. 农业机械学报,2016,47(9): 398-405. doi: 10.6041/j.issn.1000-1298.2016.09.053QI Jibao, YANG Weimin. Differential change construction based geometric error compensation for machine tools[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(9): 398-405. doi: 10.6041/j.issn.1000-1298.2016.09.053 VEITSCHEGGER W K, WU C H. Robot accuracy analysis based on kinematic[J]. Robot Automatic, 1986, RA-2(1): 227-233. ZHAI X C, DU Q G, WANG W X, et al. A new approach to tolerance analysis based on tracking local coordinate systems[J]. Journal of Advanced Mechanical Design Systems and Manufacturing, 2017, 11(2): 1-8. DESROCHERS A, RIVIERE A. A matrix approach to the representation of tolerance zones and clearances[J]. International Journal of Advanced Manufacturing Technology, 1997, 13(9): 630-636. doi: 10.1007/BF01350821 YARON O B, LEO J. Tolerance envelopes of planar mechanical parts with parametric tolerances[J]. Computer Aided Design, 2005, 37(5): 531-544. doi: 10.1016/j.cad.2004.07.005 DU Q, ZHAI X, WEN Q. Study of the ultimate error of the axis tolerance feature and its pose decoupling based on an area coordinate system[J]. Applied Sciences, 2018, 8(3): 435. doi: 10.3390/app8030435 杜群贵,翟晓晨,文奇,等. 基于刚体运动学的复杂装配体递推误差分析[J]. 华南理工大学学报(自然科学版),2017,45(9): 26-33.DU Qungui, ZHAI Xiaochen, WEN Qi, et al. A recursive approach to tolerance analysis of complex assembly based on rigid body kinematics[J]. Journal of South China University of Technology (Natural Science Edition), 2017, 45(9): 26-33. 全毅. 箱体公差对变速箱力学性能的影响[D]. 广州: 华南理工大学, 2015. 方宗德,郭琳琳,苏进展,等. 基于齿面印痕控制的弧齿锥齿轮公差优化设计[J]. 农业机械学报,2011,42(7): 223-228.FANG Zongde, GUO Linlin, SU Jinzhan, et al. Optimal design of tolerance for spiral bevel gears by controlling contact path[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(7): 223-228. ABBES M S, FAKHFAKH T, HADDAR M, et al. Effect of transmission error on the dynamic behaviour of gearbox housing[J]. International Journal of Advanced Manufacturing Technology, 2007, 34(3/4): 211-218. doi: 10.1007/s00170-006-0582-7 -
下载:
点击查看大图
图(8) / 表(1)
计量
- 文章访问数: 570
- HTML全文浏览量: 316
- PDF下载量: 9
- 被引次数: 0