Seismic Collapse-Resistant Performance of Stone Houses in Tibetan and Qiang Autonomous Prefectures of Western Sichuan
-
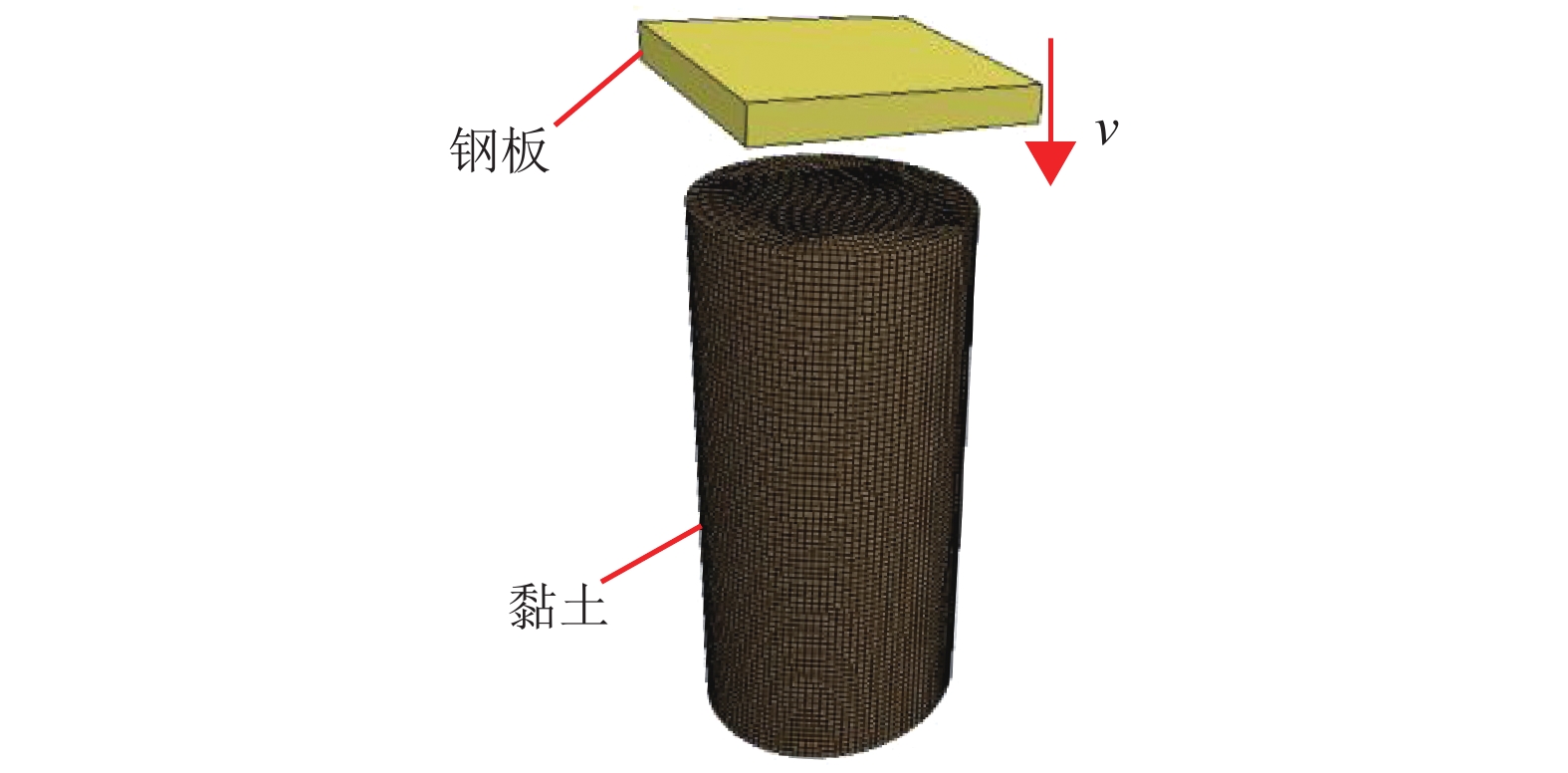
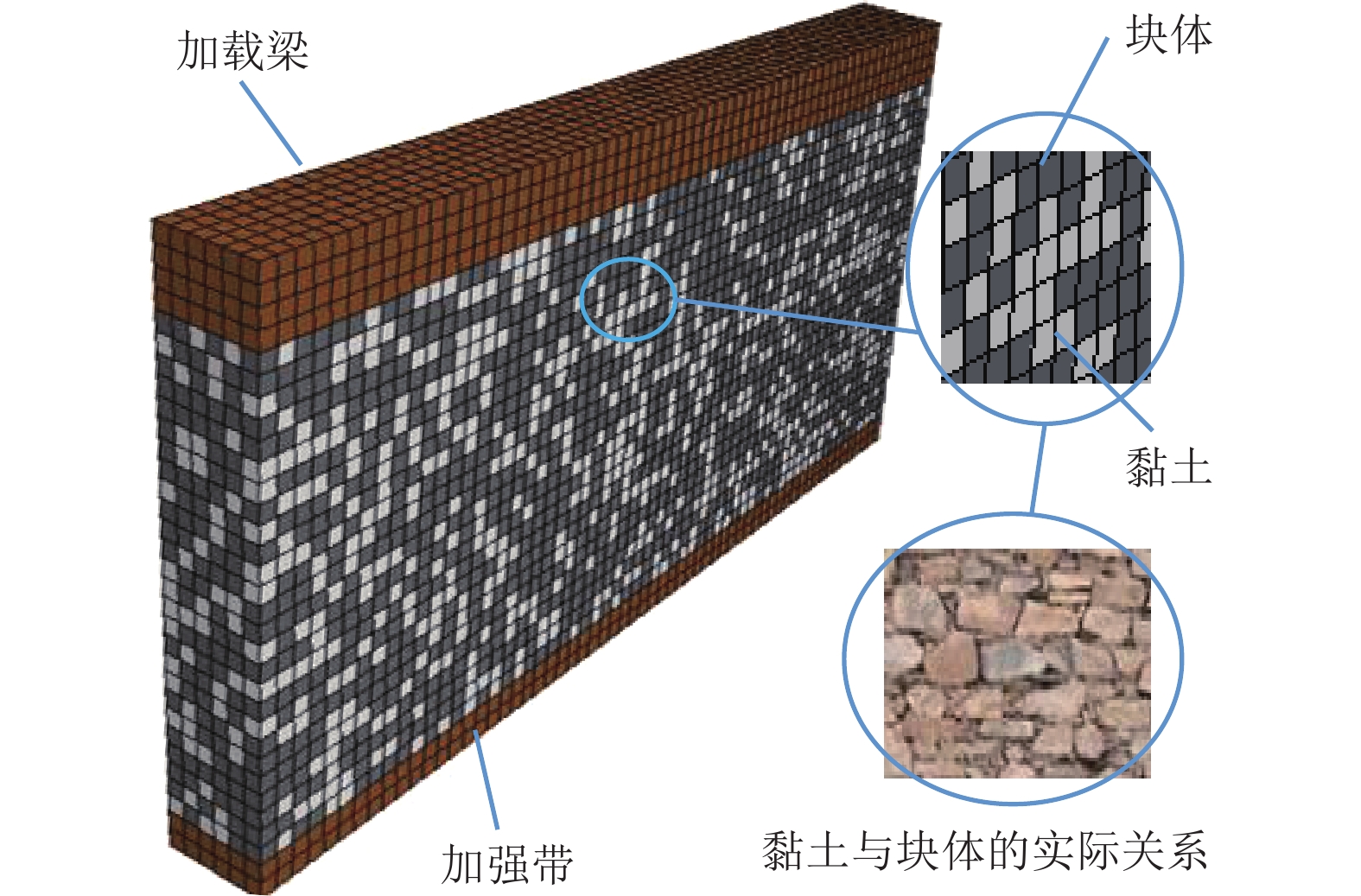
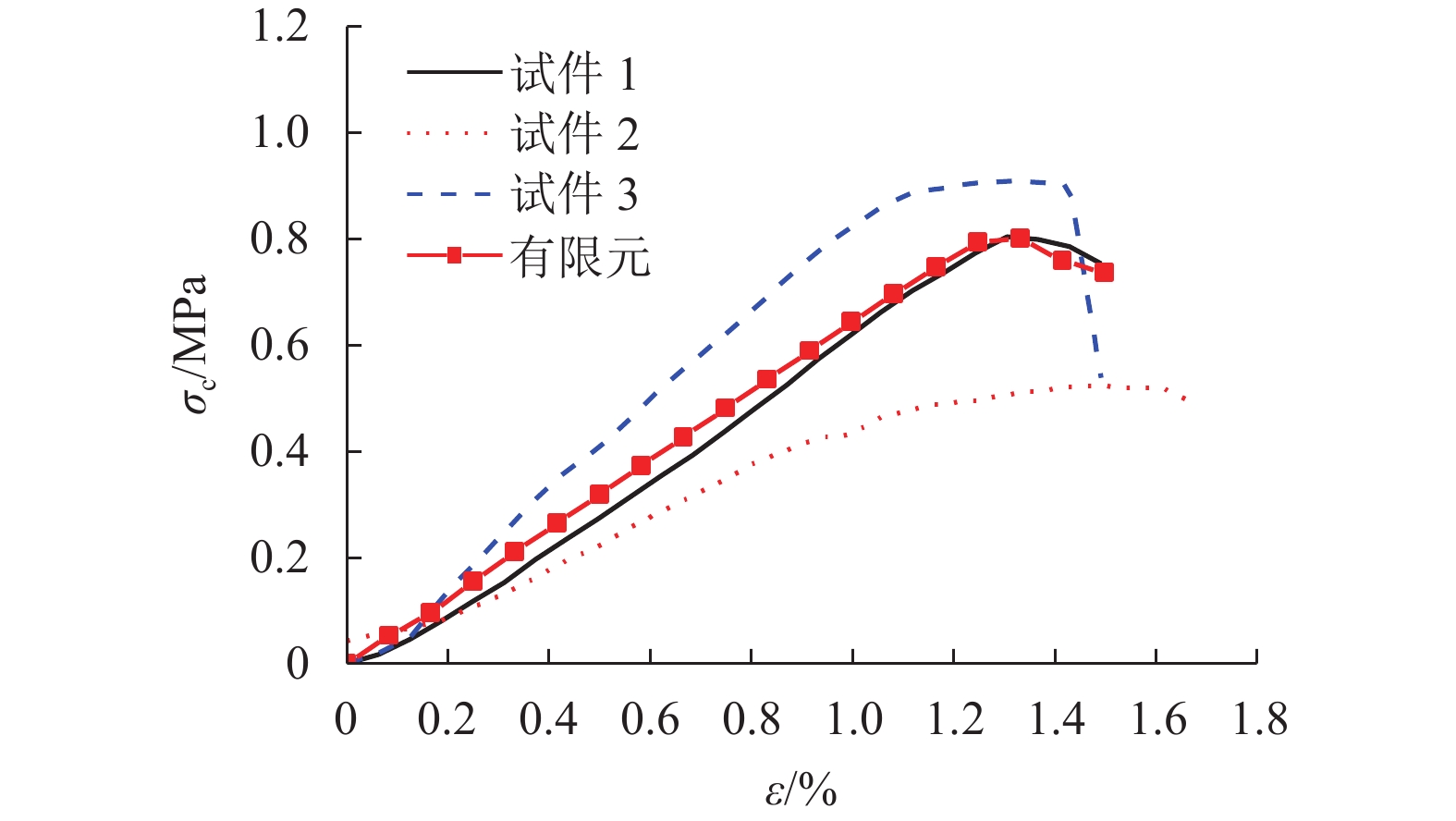
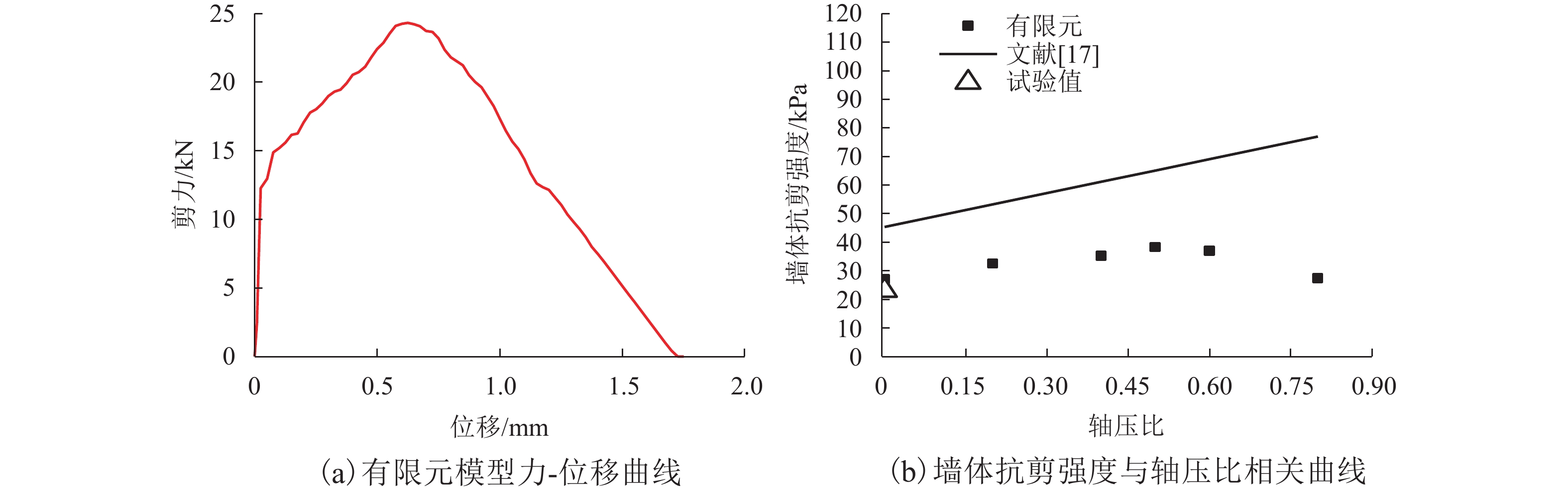
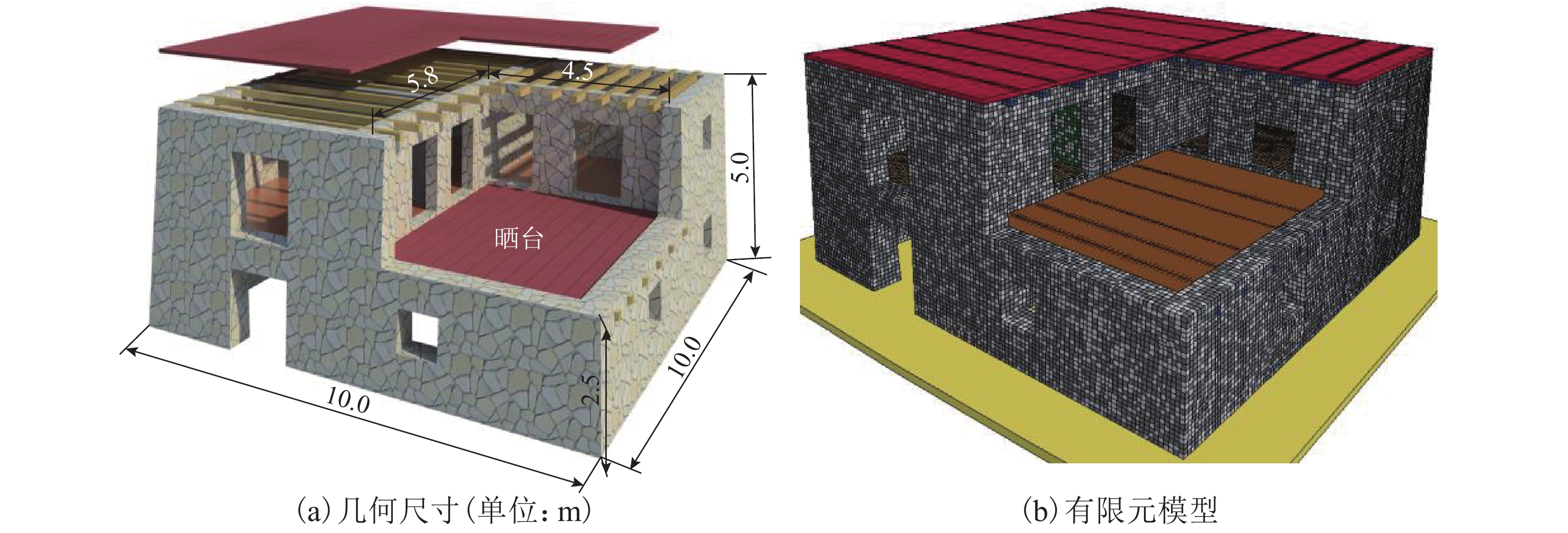
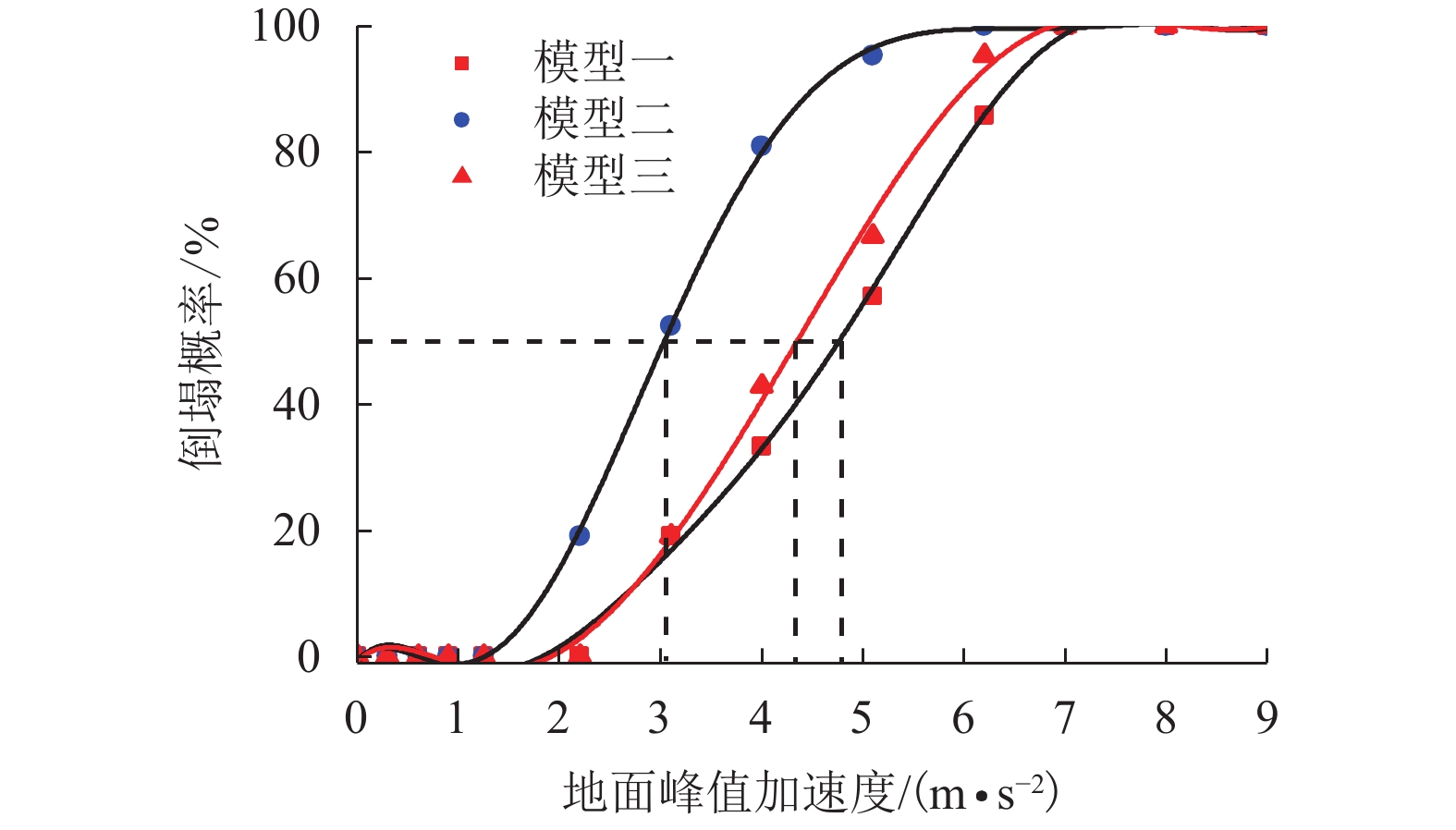
摘要: 我国川西地区的传统藏羌石砌民居具有较高的文化遗产保护价值，但在近年来的历次地震中出现了大量破坏. 结合该类房屋的砌筑材料和建筑布置特征，对其抗地震倒塌性能进行研究. 首先，开展了3组黏土试件的无侧限抗压强度试验和一个1/2缩尺黏土-石砌墙体试件的水平抗剪承载力试验，并通过显式动力数值计算手段对试验过程进行模拟；其次，针对黏土和毛石材料均采用Holmquist-Johnson-Cook （HJC）本构模型，基于随机分布离散型有限元方法，根据实际墙体中两种材料的分布比例建立相应数值模型，并通过与模型试验结果的对比验证，明确了数值计算中的关键参数；在此基础上，对一典型二层平面L型缩进式民居结构进行动力时程分析计算，通过与实际震害情况的对比分析了其地震破坏机制，再现了地震倒塌全过程，并开展了结构的抗地震倒塌易损性分析，研究了不同晒台缩进面积的影响. 研究结果表明，在罕遇烈度下，平面L型缩进式结构中晒台面积比例由30%增加至45%时，结构倒塌概率增大16.7%，抗倒塌储备系数下降9%，对易损性曲线影响并不显著；但当晒台面积比例减小至15%时，二层墙体开洞率增大18%，导致结构的地震倒塌概率增加143%.
-
关键词:
- 砌体结构 /
- 民居碉房 /
- 随机分布离散型有限元模型 /
- 抗震性能 /
- 易损性分析
Abstract: Traditional stone houses in the Tibetan and Qiang autonomous prefectures of Western Sichuan, deserve preservation as indicators of cultural heritage; however many of them have been damaged during earthquakes in recent years. Based on the characteristics of masonry materials and architectural layout, seismic collapse-resistant performance of stone houses was investigated. Unconfined compression tests on three clay specimens and lateral shear tests on a half-scaled clay-brick rubble masonry wall specimen were conducted and also modeled via an explicit dynamic numerical approach. The Holmquist–Johnson–Cook (HJC) constitutive model was applied to the clay and rubble, and a randomly-distributed discrete finite element model was built to show the proportion between clay and brick rubble. Through the comparison of experimental and numerical results, the numerical model was verified and key parameters were calibrated. According to above work, a structural model of a typical two-storey residential stone house with an L-shaped indented platform was built, and its dynamic time-history analysis was conducted. By comparing the calculated seismic damage modes with its real seismic damage, the collapse mechanism was analyzed and the collapse process was simulated. Moreover, the structural fragility of seismic collapse was studied based on the influence of the indented area of the platform. The results indicate that, under rare seismic intensity, when the indented area is increased from 30% to 45%, the probability of structural collapse increases by 16.7%, and the collapse margin ratio decreases by 9%, which has little effect on the fragility curve. However, when the indented area is reduced to 15%, the failure rate of walls on the second floor increases by 18%, leading to the increase of 143% in the probability of structural collapse. -
兰新高铁地处中国西北地区，东起兰州，西至乌鲁木齐，全长1776 km，是世界上第一条一次性建成运营里程最长的高速铁路. 线路穿越我国新疆地区的百里、三十里等四大风区，风区内常年盛行七八级大风，曾发生过列车被大风吹翻的重大铁路安全事故[1]. 为保证列车安全顺利地通过风区，铁路建设部门在风区线路轨旁修建了高度为3.5～4.0 m的挡风墙. 但挡风墙“防车不防网”，气流经过挡风墙之后出现了明显的加速效应，使得正馈线发生剧烈舞动，导致线间放电、金具磨损加剧、线索疲劳断股，危及行车安全. 由于铁路运输对安全性要求很高，能够采用的防舞措施有限，低风压正馈线不改变接触网结构，有较好的适应性. 因此，设计一种新型低风压正馈线，用于降低正馈线的舞动幅值，保障牵引变电系统的安全可靠运行十分必要.
作用于架空输电导线的风载荷占整个线路所受风载荷的50%以上[2]，降低正馈线所受风压不仅可以减小线索舞动幅值，还可以降低因线间放电而引起的跳闸风险. 20世纪70年代，日本关西电气与住友电气等单位对多种不同表面形状的导线进行了风洞试验，研究结果表明，导线风阻力系数与导线表面形状有较大关系[3]. 20世纪90年代起，关西电气和住友电气对低风压导线的运行机理进行了持续研究，研究结果表明，低风压导线负压区面积小于普通导线，风阻力系数较小[4-5]. 我国在低风压导线领域起步较晚，但发展较快. 近年来，上海电缆研究所、无锡华能电缆有限公司、江苏中天科技股份有限公司等单位研发了不同表面结构的低风压导线产品，并申请了专利[6].
以6种不同表面形状的低风压正馈线和常规正馈线模型为研究对象，对各型正馈线在12～24 m/s （间隔3 m/s）风载荷作用下的舞动情况进行仿真，监测记录不同型号的低风压正馈线和常规正馈线在不同风载荷下的风阻力系数和跨距中点位移值，分析低风压正馈线表面结构参数对风阻力系数和跨距中点位移值变化的影响规律；对不同风载荷作用下风阻力系数较小的低风压正馈线建立三维有限元模型，并施加轴向拉力，分析其在轴向拉力作用下的形变及应力情况，研究成果为低风压正馈线的制造、选型及现场维护提供理论依据.
1. 模型建立
以现场架设的常规正馈线作为依据，建立常规正馈线二维模型，其二维截面结构如图1所示. 图中，R = 11.88 mm，为正馈线半径. 正馈线是由2层钢股和3层铝股相互绞合而成，其中，钢股直径为2.22 mm，铝股直径为2.85 mm.
图 1 常规正馈线二维截面示意Figure 1. Two-dimensional cross-sectional diagram of conventional catenary positive feeder本文以低风压导线运行机理为基础，设计凹槽数为8、不同凹槽半径的6种低风压正馈线模型，其中，一种低风压正馈线模型截面结构如图2所示，线径均为23.76 mm. 与常规正馈线相比，低风压正馈线模型的最外层由8根中间带有凹槽的铝股线构成，凹槽的小圆弧半径r 与常规正馈线半径R的比值为0.10～0.15，其余层股线结构参数与常规正馈线相同.
图 2 r/R = 0.14型低风压正馈线截面示意Figure 2. Cross-sectional diagram of low-wind-pressure catenary positive feeder with r/R = 0.142. 仿真计算与分析
2.1 仿真计算
对r/R = 0.10～0.15的6种低风压正馈线和常规正馈线模型进行12、15、18、21、24 m/s风载荷下的气动力特性仿真. 首先，设置计算域边界条件，将计算域左侧边界设置为速度入口，导线表面采用无滑移壁面边界，右侧边界设置为压力出口. 迭代收敛残差值取1 × 10−5，时间步长为0.005 s，计算1000步，以r/R = 0.14型低风压正馈线为例，仿真计算得到常规正馈线和低风压正馈线在18 m/s风载荷下的阻力系数CD时程图，如图3所示. r/R = 0.14型低风压正馈线在18 m/s风载荷下的阻力系数时程曲线幅值明显小于常规正馈线，为各低风压正馈线中阻力系数幅值最小的一种. 对45 m跨距正馈线在只受重力作用下线索悬垂状态找形成功后，将阻力系数以线性插值的方式添加，得到常规正馈线和r/R = 0.14型低风压正馈线跨距中点在18 m/s风载荷作用下的垂向位移时程图，如图4所示. 在同一坐标系下，r/R = 0.14型低风压正馈线垂向位移曲线幅值明显小于常规正馈线，即r/R = 0.14型低风压正馈线能够降低舞动幅值.
2.2 气动力参数分析
对6种低风压正馈线和常规正馈线在不同风载荷下的气动力特性进行仿真计算，得到不同线型在不同风载荷下的阻力系数，如图5所示. 统计6种低风压正馈线在18 m/s风载荷作用下跨距中点横向和垂向位移最大值，如图6所示.
图 5 不同低风压正馈线模型阻力系数曲线Figure 5. Drag coefficient curves for different types ofcatenary positive feeder models由图5可知，常规正馈线和6种低风压正馈线风阻力系数基本上随风速的增大呈减小趋势，且在整个测试风速范围内，低风压正馈线阻力系数均小于常规正馈线，说明本文设计的低风压正馈线模型具有防舞效果. 其中：常规正馈线气动力参数在整个测试风速范围内随风速的增大而减小， r/R = 0.10～ 0.11型低风压正馈线阻力系数交替出现下降和上升；r/R = 0.12～0.15型低风压正馈线阻力系数先上升之后一直下降；r/R = 0.14型低风压正馈线除在24 m/s风速时阻力系数略大于r/R = 0.15外，在其余测试风速时阻力系数均小于其他测试对象，为测试对象中降阻效果最好的线型.
由图6可知，常规正馈线跨距中点横向位移最大值为1.338 m，垂向位移最大值为1.240 m，低风压正馈线跨距中点位移最大值均较常规正馈线小，且最大位移值随r/R值的增大整体上呈现下降的趋势，但r/R = 0.15型低风压正馈线位移最大值较r/R = 0.14型低风压正馈线大，说明低风压正馈线设计的关键在于找到恰当的r/R值；r/R = 0.14型低风压正馈线位移幅值最小，其横向位移最大值为0.990 m，垂向位移最大值为0.910 m，较常规正馈线分别下降26.0%和26.6%，与图5风阻力系数相对应，说明了本文仿真方法的合理性以及仿真结果的准确性.
3. 低风压正馈线受力特性分析
正馈线在舞动过程中线夹出口处会产生大小不断变化的集中应力，会加剧连接金具的磨损以及线索疲劳断股. 为研究低风压正馈线在舞动时的受力特性，根据国际大电网会议的建议，以线夹出口89 mm处导线的动弯应变来评估低风压正馈线的运行状况[7]. 对图5、6各正馈线仿真结果分析发现，r/R = 0.12，0.13，0.14型3种低风压正馈线防舞效果较佳. 因此，建立3种低风压正馈线89 mm长度三维模型，在有限元软件中对自由端面施加一定拉伸载荷，模拟正馈线舞动时的受力情况，分析低风压正馈线发生舞动时的形变量及应力特性[8-9].
3.1 建立有限元模型
兰新高铁现场架设的常规正馈线结构参数如表1所示，该正馈线铝的杨氏模量为59 GPa，泊松比为0.30，钢的杨氏模量为190 GPa，泊松比为0.28，额定拉断力为83.42 kN. 本文以常规正馈线结构参数为依据，建立89 mm长度低风压正馈线三维模型，在固定端建立三维坐标轴O-XYZ. 其中，r/R = 0.14型低风压正馈线三维模型如图7所示，最外层铝股线中央带有凹槽，股线数为8股，其他层股线结构参数与常规正馈线相同.
表 1 常规正馈线结构参数Table 1. Structural parameters of conventional positive feeder材料 层数 股数/股 直径/mm 节径/mm 节距/mm 绞向 钢 最内层 1 2.22 次内层 6 2.22 21 139.86 左 铝 次外层 10 2.85 13 160.68 右 邻外层 16 2.85 12 216.72 左 最外层 22 2.85 11 261.36 右 
图 7 r/R = 0.14型低风压正馈线三维模型Figure 7. Three-dimensional model of positive feeder with r/R = 0.143.2 仿真方法验证
1） 仿真设置. 在有限元软件中设置钢铝股线的材料属性，将每根股线的中心节点等效为一个整体，在相邻股线之间建立接触对. 在设置边界条件时，将正馈线模型位于线夹一端完全固定约束，即在模型的固定端端面上约束X、Y、Z 3个方向的自由度. 为防止产生端部效应，在模型的自由端端面上建立一个刚域点，将该端面上所有自由度与该刚域点耦合形成一个刚域面，在刚域点上施加运行张力. 最后，采用扫掠法对模型进行正六面体网格划分[10-12]，得到的模型网格图如图8所示.
2） 方法验证. 我国一般将导线的运行张力设定为15%～25% 额定拉断力[13]（rated tensile strength，RTS），兰新高铁考虑正馈线新线系数后正馈线的最大许用张力为32137 N，为额定拉断力的38.5%，但正馈线长期在最大许用张力下运行，容易导致疲劳断股. 本文对常规正馈线施加25% RTS，即20.855 kN拉力，仿真得出各层股线轴向张力，将仿真结果与式（1）正馈线各层股线理论张力计算式结果进行对比[14]，结果见表2.
表 2 常规正馈线各层股线轴向张力Table 2. Axial tension of each layer of conventional positive feederkN 材料 层数 理论值 仿真值 误差 钢 最内层 5.963 5.921 0.242 次内层 7.839 7.818 0.221 铝 次外层 3.956 3.651 0.305 邻外层 5.045 4.889 0.156 最外层 3.383 3.112 0.271 Fn=πd2n4znEncosαn×cos(αn√(1+εi)2+(tanαn−μεi)2−1)， (1) 式中：Fn为第n层股线轴向张力；dn为股线直径；zn为股线数；En为股线弹性模量；αn为拉伸前股线捻角；εi为股线轴向伸长率；μ为该层股线的泊松比.
由表2可知，常规正馈线在25% RTS作用下，2层钢芯承担了54.1%的拉力，3层铝股线承担了45.9%的拉力，这与正馈线的设计初衷和现场运行情况相符. 仿真值与理论值存在一定误差，是因为理论计算时未考虑股线之间的挤压和摩擦对正馈线应力的影响. 但误差仍处于合理范围内，故本文所采用的仿真方法能够恰当地模拟正馈线在受到轴向拉力时的应力-应变特性.
3.3 结果分析
3.3.1 低风压正馈线受力形变及应力分析
在有限元软件中对r/R = 0.12，0.13，0.14型低风压正馈线三维模型自由端面施加25% RTS，分别比较3种正馈线的形变位移及应力变化情况[15-16]. 其中，r/R = 0.14型低风压正馈线在施加25% RTS后，轴向整体形变及各层股线轴向形变如图9所示.
图 9 r/R = 0.14型低风压正馈线形变云图Figure 9. Deformation nephogram of positive feeder with r/R = 0.14由图9（a）可知，正馈线在受到轴向拉力的作用下会发生一定轴向形变，固定端形变量最小，越往自由端，形变量越大，这与现实情况相吻合. 由图9（b）可知，各层股线在受到轴向拉力的情况下，形变量是不同的，轴向形变量从钢层到铝层逐渐增大，至最外层铝股线达到最大，即在现实中正馈线舞动时，最外层铝股线最容易发生金属疲劳断股，这是由于钢的杨氏模量大于铝的杨氏模量，铝的延展性较钢强[17-18]，在同一拉力作用下，铝的形变量大于钢. 其次，正馈线在受到轴向拉力时，内层股线受到外层股线的挤压，使得内层股线的形变量小于外层股线.
对r/R = 0.14型低风压正馈线施加25% RTS，等效应力云图见图10，其纵向中心截面应变及形变云图见图11.
图 10 r/R = 0.14型低风压正馈线应力Figure 10. Stress nephogram of positive feeder with r/R = 0.14
图 11 r/R = 0.14型低风压正馈线轴向截面云图Figure 11. Axial section nephogram of positive feeder with r/R = 0.14由图10（a）可知，次内层钢股线在正馈线振动时承担了大部分轴向应力，且除最内层直钢股应力分布均匀外，其他层股线应力分布不均，但具有一定的规律，即应力极值点的位置与正馈线每层股线的绞向相同，这是因为正馈线在轴向拉力作用下，同层相邻股线在绞合方向上相互挤压，形成应力集中点. 从图10（b）可知，钢股等效应力远大于铝股，即在正馈线舞动时钢股承受了很大一部分应力，且应力在直钢芯两侧对称分布，应力从固定端和自由端到中间的变化趋势相似，保证了正馈线受力对称.
由图11（a）可知，股线轴向应变沿最内层钢股两侧对称分布，中心钢股承受了最大拉变，这符合正馈线的设计初衷，邻外层钢股出现了最大压变，这是因为该层股线受到相邻两层股线的挤压. 从图11（b）可知，由固定端到自由端整体形变量逐渐增大，自由端形变量远大于固定端；由于中心钢股非螺旋结构，且钢的杨氏模量大，延展性较铝差，抗拉强度大，所以形变量最小；次内层钢股和邻外层铝股在绞线中间位置附近受到相邻股线的严重挤压，出现了最大形变量.
对r/R = 0.14型低风压正馈线施加25% RTS，沿轴向坐标轴Z轴截取固定端Z = 0至自由端端面，间隔8.9 mm，共11个轴向应力截面，分析其轴向应力，其中4个应力截面如图12所示.
图 12 25% RTS作用下r/R = 0.14型低风压正馈线横向截面应力云图Figure 12. Stress nephogram of horizontal cross-section of positive feeder with r/R = 0.14 under 25% RTS由图12可知，正馈线在轴向载荷作用下会发生一定程度的扭转. 正馈线的不同截面轴向应力分布不同，中心直钢芯上应力分布较均匀，螺旋钢层和铝层同一股线应力呈阶梯状分布，且应力极值点位置与正馈线层绞合方向相关；从固定端端面到自由端端面的不同截面上，应力极值点位置从与绞合方向相反到与绞合方向相同，但均位于股线接触处，说明在股线接触位置容易出现应力集中点，易引起股线磨损断股；中间位置截面轴向应力呈现中心对称，且在提取的截面中应力最小，轴向应力整体上呈现两端大中间小的情况.
3.3.2 3种低风压正馈线受力特性比较
为更准确地反映3种低风压正馈线在25% RTS作用下的受力特性，对状态变化参数进行比较，得到3种低风压正馈线25% RTS作用下状态参数变化曲线，如图13所示.
图 13 3种低风压正馈线25% RTS作用下状态参数变化曲线Figure 13. Variation of state parameter for the three types of positive feeders under 25% RTS由图13（a）可知，2层钢股承受了绝大部分应力，邻外层铝股在3层铝股中承受的应力最大，不同型号低风压正馈线在25% RTS作用下，从内向外第1、4层股线承受的应力基本相同，最外层股线最大应力随r/R值的增大而增大. 由图13（b）可知，在轴向拉力的作用下，股线位移量从内层到外层依次增大，表明最外层铝线最容易疲劳断股. 由于中心钢股没有螺旋，抗拉强度大，所以r/R = 0.12，0.13，0.14型低风压正馈线中心钢股位移量基本相等，r/R = 0.13，0.14型低风压正馈线第2、4层股线位移量基本相等；r/R = 0.12型低风压正馈线第2、5层股线位移量均小于其他低风压正馈线，第5层股线位移量随r/R值的增大而增大.
4. 结 论
通过对设计的低风压正馈线进行防舞有效性仿真分析，发现低风压正馈线达到了预期效果，并对其中3种防舞效果较佳的低风压正馈线进行受力特性分析，得出以下结论，并对低风压正馈线的制造、选型及现场维护给出以下建议：
1） 低风压正馈线在受到轴向拉力时，铝股线的轴向形变量大于钢股线，为了平衡正馈线抗拉强度和导电性能，在制造正馈线时可以考虑将钢股线和铝股线交替绞制.
2） 在轴向载荷作用下，低风压正馈线在线夹处受到很大的应力，加剧了正馈线与线夹的磨损，容易导致股线断裂. 在正馈线的日常维护中应该加强巡视，确保线夹转动灵活，减小线夹处正馈线的静应力.
3） 低风压正馈线在轴向载荷作用下会发生一定程度的扭转，在股线接触处出现应力集中点，应力集中点位置与正馈线绞合方向相关. 在制造正馈线时可以考虑在股线表面覆缓冲层，减缓股线之间的振荡冲击，延长正馈线使用寿命.
4） 对3种防舞效果较为理想的低风压正馈线进行受力分析，发现在同一轴向载荷作用下，最外层铝股线层的位移量与r/R比值成正比例关系. 而r/R值越大，最外层铝股线横截面积越小，在正馈线舞动时越容易疲劳断股，因此，在低风压正馈线选型时应该综合考虑，平衡防舞有效性与使用寿命.
致谢：兰州交通大学天佑创新团队计划（TY202010）资助.
-
图 6 随机分布离散型墙体有限元模型
Figure 6. Randomly-distributed discrete finite element model of wall
表 1 HJC本构模型参数
Table 1. Key parameters of HJC constitutive model
参数 黏土 毛石 参数 黏土 毛石 ρ/（kg•m–3） 1 750 2 800 Smax 7 20 G/MPa 71.4 1 357 Pcrush/MPa 1.19 81.5 A 0.79 0.55 μcrush/× 10–3 3.57 12.9 B 1.6 1.23 PLock/GPa 2 2 C/× 10–3 7 9.7 μLock/× 10–1 1.74 1.74 N 0.61 0.89 D1/× 10–2 4.87 4 f’c/MPa 0.99 67.92 D2 1 1 T/MPa 0.042 2 K1/MPa 85 39 ε0/× 10–6 1 1 K2/MPa –171 –223 εf，min 0.01 0.01 K3/MPa 208 550 
下载: 导出CSV
-
林建华,王全凤,施养杭. 石砌体结构抗震性能及其模糊抗震可靠度的研究[J]. 土木工程学报,1998,31(6): 40-48.LIN Jianhua, WANG Quanfeng, SHI Yyanghang. Study on the seismic behaviour and fuzzy earthquake-resistant reliability of stone masonry structures[J]. China Civil Engineering Journal, 1998, 31(6): 40-48. 张淑娴. 粗料石砌体房屋振动台试验研究[D]. 南京: 东南大学, 2015 陶毅,古金本,信任,等. CFRP网格加固震损多层砌体开洞墙体的抗震性能研究[J/OL]. 西南交通大学学报, 网络优先出版. （2018-05-22）[2018-08-01]. http://kns.cnki.net/kcms/detail/51.1277.U.20180522.2227.006.htmlTAO Yi, GU Jinben, XIN Ren, et al. Seismic performance of multi-storey masonry wall with opening repaired using CFRP grid[J/OL]. Journal of Southwest Jiaotong University, Network Priority Publishing. (2018-05-22) [2018-08-01]. http://kns.cnki.net/kcms/detail/51.1277.U.20180522.2227.006.html 徐学书,喇明英. 羌族传统建筑抗震技术及其传承研究[J]. 西南民族大学学报(人文社科版),2009(2): 11-14. doi: 10.3969/j.issn.1004-3926.2009.02.003 孙建刚,崔利富,王振,等. 藏族民居砌体材料物理力学性能试验研究[J]. 大连民族学院学报,2015,17(1): 61-64. doi: 10.3969/j.issn.1009-315X.2015.01.016SUN Jiangang, CUI Lifu, WANG Zheng, et al. Experiment research of stone masonry materials physical mechanic property of Tibetan folk house[J]. Journal of Dalian Nationalities University, 2015, 17(1): 61-64. doi: 10.3969/j.issn.1009-315X.2015.01.016 杨惠晴. 藏族民居抗震性能数值仿真分析——以木堆藏寨194号为例[D]. 大庆: 东北石油大学, 2014 刘伟兵,崔利富,孙建刚,等. 藏族民居石砌体基本力学性能试验与数值仿真[J]. 大连民族学院学报,2015,17(3): 252-256. doi: 10.3969/j.issn.1009-315X.2015.03.015LIU Weibing, CUI Lifu, SUN Jiangang, et al. Tests and numerical simulation of basic mechanical properties of Tibetan dwellings stone masonry[J]. Journal of Dalian Nationalities University, 2015, 17(3): 252-256. doi: 10.3969/j.issn.1009-315X.2015.03.015 张先进. 汶川大地震对藏、羌村寨聚落的破坏与恢复思考[C]//中国民族建筑研究会学术年会暨第二届民族建筑（文物）保护与发展高峰论坛. 北京: 中国民族建筑研究会, 2008: 171-174 中华人民共和国水利部. 土工试验方法标准: GB/T 50123—1999[S]. 北京: 中国计划出版社, 1999 苗吉军,顾祥林,张伟平,等. 地震作用下砌体结构倒塌反应的数值模拟计算分析[J]. 土木工程学报,2005,38(9): 45-49. doi: 10.3321/j.issn:1000-131X.2005.09.008MIAO Jijun, Gu Xianglin, Zhang Weiping, et al. Numerical simulation analysis for the collapse response of masonry structures under erthquakes[J]. China Civil Engineering Journal, 2005, 38(9): 45-49. doi: 10.3321/j.issn:1000-131X.2005.09.008 许浒,李勇志,雷敏,等. 群落生土建筑的抗地震倒塌加固措施[J]. 工程抗震与加固改造,2017,39(1): 135-142.XU Hu, LI Yongzhi, LEI Min, et al. A strengthening measure for seismic collapse resistance of the residential[J]. Earthquake Resistant Engineering And Retrofitting, 2017, 39(1): 135-142. 李耀. 混凝土HJC动态本构模型的研究[D]. 合肥: 合肥工业大学, 2016 陕西省建筑科学研究院. 建筑砂浆基本性能试验方法标准: JGJ/T 70—2009[S]. 北京: 中国建筑工业出版社, 1999 方秦,孔祥振,吴昊,等. 岩石Holmquist-Johnson-Cook模型参数的确定方法[J]. 工程力学,2014,31(3): 197-204.FANG Qin, KONG Xiangzhen, WU Hao, et al. Determination of Holmquist-Johnson-Cook constitutive model parameters of rock[J]. Engineering Mechanics, 2014, 31(3): 197-204. 于文. 新疆喀什生土石房屋模型振动台试验研[D]. 北京: 中国建筑科学研究院, 2007 甄昊. 阿坝州生土石砌体结构在地震作用下的抗倒塌分析[D]. 成都: 西南交通大学, 2016 工程地质手册编写委员会, 工程地质手册[M]. 3版. 北京: 中国建筑工业出版社, 1992: 214-216 施景勋,卢志红,林建华,等. 对石墙抗震性能的研究和设计取值的建议[J]. 华侨大学学报(自然科学版),1993,14(2): 197-198.SHI Jingxun, LU Zhihong, LIN Jianhua, et al. Syudy on the antiseismic behavior of stone wall and proposal of the short-cut process in its design[J]. Journal of Huaqiao University (Natural Science), 1993, 14(2): 197-198. 余卓群. 四川藏寨传统住宅述略[C]//中国民族聚居区建筑文化遗产国际研讨会论文集. 成都: [出版者不详], 2010: 119-123 朱荣张. 马尔康直波藏寨民居建筑研究[D]. 西安: 西安建筑科技大学, 2012 孙玉红,聂立武,韩古月,等. 地震作用下建筑结构倒塌失效准则分析[J]. 中外建筑,2011,35(18): 199-201.SUN Yuhong, NIE Liwu, HAN Guyue, et al. Analysis on the rules of architecture structure tumble invalidation earthquake function[J]. Chinese and Overseas Architecture, 2011, 35(18): 199-201. 焦双健,冯启民,付长文,等. 钢筋混凝土框架结构地震破坏的计算机模拟方法[J]. 地震工程与工程振动,2002,22(2): 54-59. doi: 10.3969/j.issn.1000-1301.2002.02.009JIAO Shuangjian, FENG Qimin, FU Changwen, et al. Simulation method for earthquake damage to RC frames[J]. Earthquake Engineering and Engineering Vibration, 2002, 22(2): 54-59. doi: 10.3969/j.issn.1000-1301.2002.02.009 中华人民共和国住房和城乡建设部. 建筑抗震设计规范: GB50011—2010[S]. 北京: 中国建筑工业出版社, 2010 FEMA. NEHRP guidelines for seismic rehabilitation of builidings[R]. FEMA Report 273. Washington D. C.: Federal Emergency Management Agency, 1997: 2-10, 2-13 李吉,刘如山,越潇. 结构抗震破坏准则研究综述[J]. 世界地震工程,2015,31(1): 262-263.LI Ji, LIU Rushan, YUE Xiao. Research summary of seismic failure criteria for structures[J]. World Earthquake Engineering, 2015, 31(1): 262-263. 许浒, 余志祥, 康翔杰, 等. 多层砌体结构在地震中倒塌全过程数值模拟[J]. 建筑结构, 2012, 42（增刊1）: 223-224XU Hu, YU Zhixiang, KANG Xiangjie, et al. Numerical simulation on collapse process of multistory masonry structure in earthquake[J]. Building Structure, 2012, 42 (S1): 223-224 Applied Technology Council. Quantification of building seismic performance factors: FEMA P695[R]. Washington D. C., Federal Emergency Management Agency, 2009. 陆新征,叶列平. 基于IDA分析的结构抗地震倒塌能力研究[J]. 工程抗震与加固改造,2010,32(1): 13-18. doi: 10.3969/j.issn.1002-8412.2010.01.003LU Xinzheng, YE Lieping. Study on the sesmic collapse resistance of structural system[J]. Earthquake Resistant Engineering and Retrofitting, 2010, 32(1): 13-18. doi: 10.3969/j.issn.1002-8412.2010.01.003 施炜,叶列平,陆新征,等. 不同抗震设防RC框架结构抗倒塌能力的研究[J]. 工程力学,2011,28(3): 42-43.SHI Wei, YE Lieping, LU Xinzheng, et al. Study on collapse-resistant capacity of RC frames with different sesmic fortification levels[J]. Engineering Mechanics, 2011, 28(3): 42-43. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 607
- HTML全文浏览量: 365
- PDF下载量: 22
- 被引次数: 0