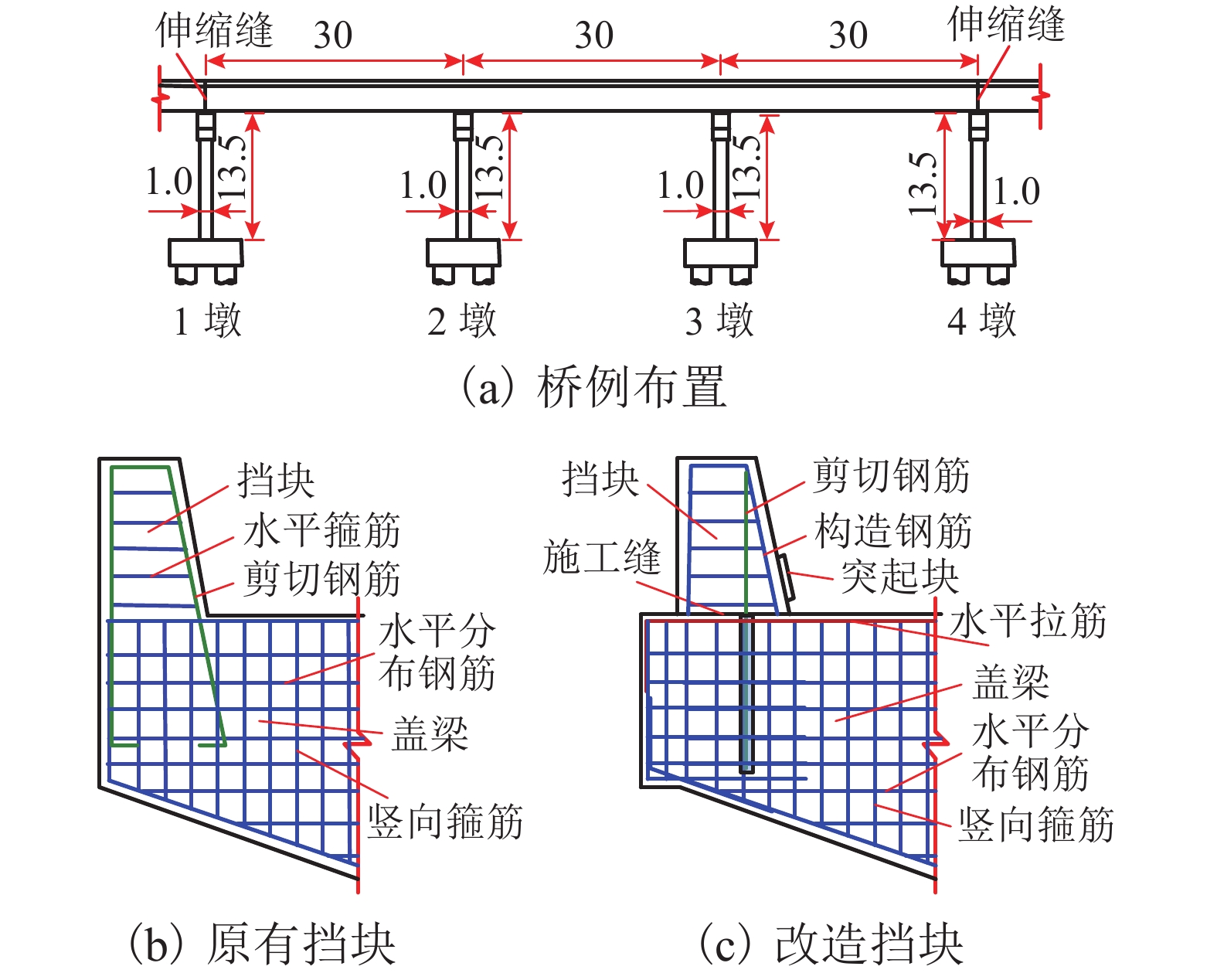
Reconstruction Method of Shear Keys on Existing Bridges Based on Structural Fuse Concept
-
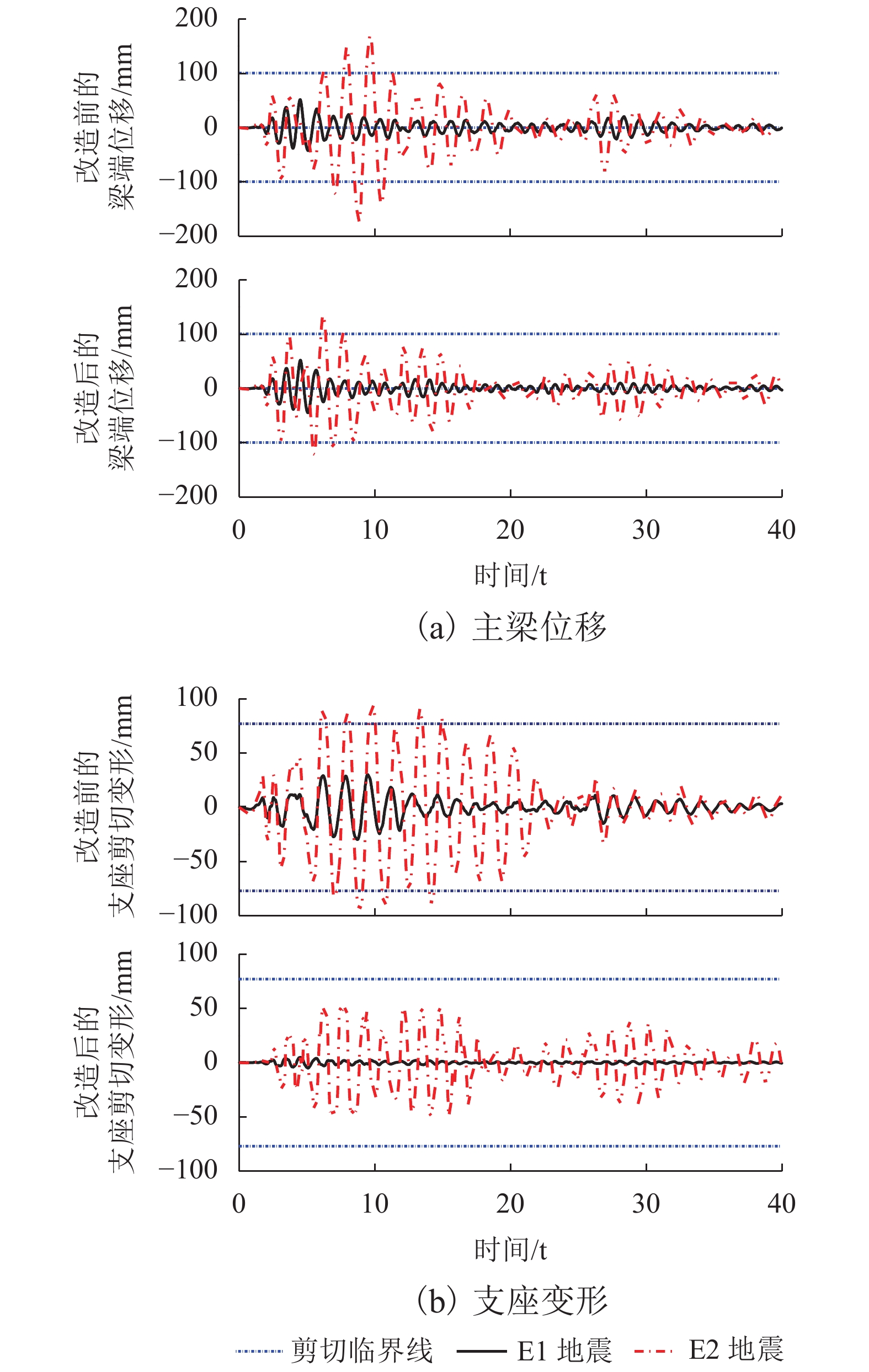
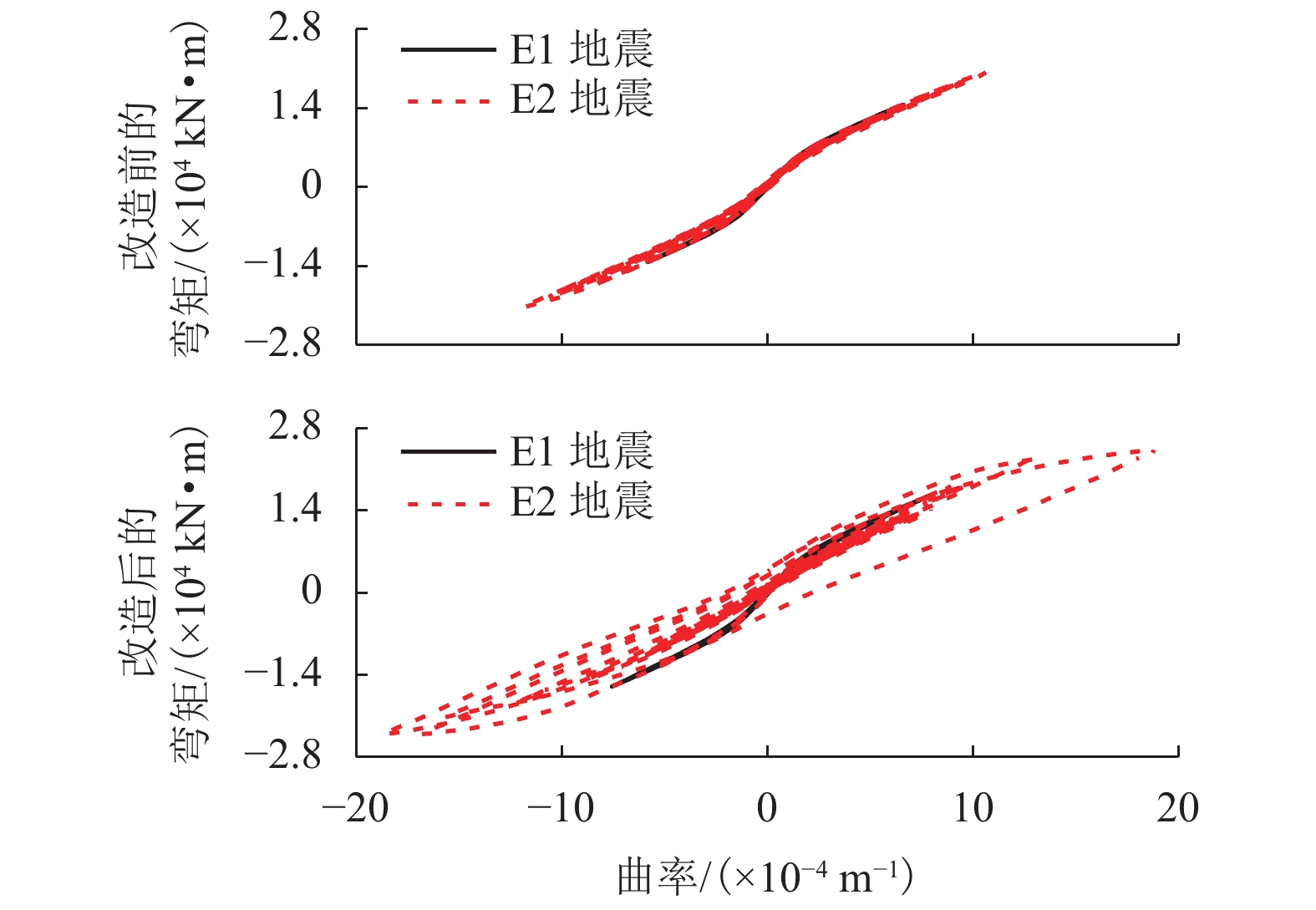
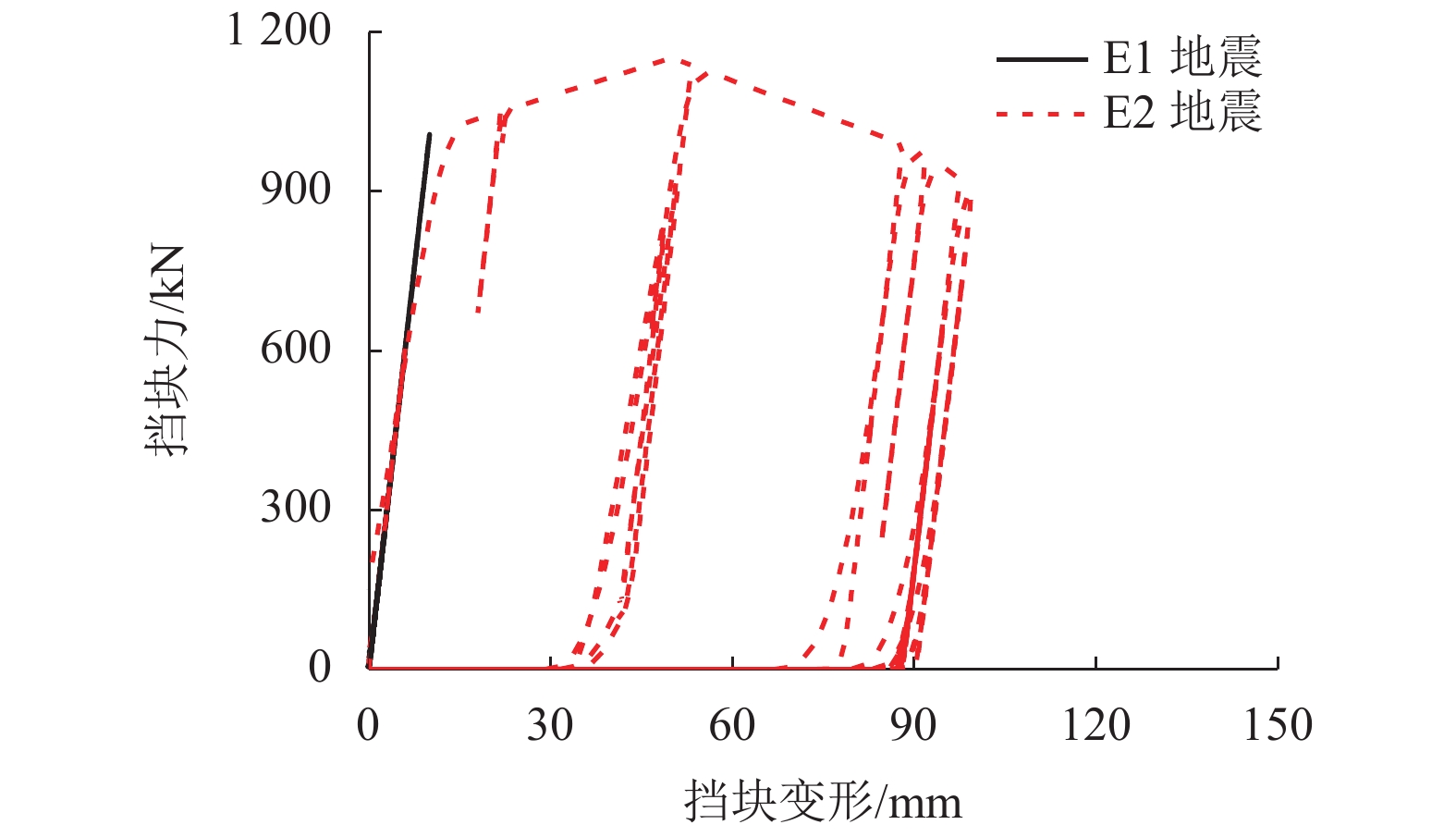
摘要: 因在役桥梁的抗震挡块在构造和配筋上缺乏规范的指导而限位效果低下，基于保险丝理念，通过改造挡块提高在役桥梁抵抗地震破坏的潜能. 首先通过拟静力试验，验证了经特定构造和配筋处理的挡块可满足保险丝理念的要求；然后，结合试验，根据滑移剪切机理建立了改造挡块的强度计算公式，并由此提出了改造挡块的具体实施细节和流程；最后，通过实桥模拟，对比分析了改造挡块的限位和传力效果. 研究结果表明：改造挡块发生大位移延性滑移剪切破坏，不会对盖梁/台帽造成损伤；改造挡块在不同设计参数下仍可采用统一的强度计算公式进行分析，计算误差普遍低于10%，大部分低于5%；实桥分析显示在E1和E2地震作用下改造挡块可使梁端侧移分别降低13.5%和22.0%，支座横向变形分别降低83.1%和45.8%；改造挡块在E1地震下处于完全弹性状态，在E2地震下处于强度退化状态，发挥了结构保险丝的作用.Abstract: Shear keys in existing bridges are ineffective in controlling the seismic displacement due to the lack of design codes to guide the details of construction and reinforcement. To improve the ability of existing bridges to resist earthquake damage, the reconstruction of shear keys based on the structural fuse concept is proposed. Firstly, quasi-static experiments are conducted to verify that the shear keys with a particular design of structural configuration and reinforcement meet the requirements of the structural fuse concept. Then, a prediction model is proposed to calculate the strength of shear keys based on the sliding shear mechanism, and the detailed procedures are presented for the reconstruction of shear keys. Finally, numerical simulations according to an actual bridge are performed to comparatively examine the effects of displacement control and force transfer of the reconstructed shear keys. The results show that the failure of reconstructed shear keys in a ductile mode with sliding shear and a large sliding displacement, causes no damage to the cap beam/stem wall. The strength of shear keys can be predicted accurately with a unified equation for different design parameters. The prediction errors of the equation are lower than 10% and most of them lower than 5%. Numerical simulations reveal that under the earthquakes of E1 and E2 levels, the reconstructed shear keys can decrease the lateral displacement of superstructure by 13.5% and 22.0%, respectively, and reduce the transverse deformation of laminated rubber bearings by 83.1% and 45.8%, respectively. The reconstructed shear keys remain perfectly elastic under the earthquake of E1 level and experience strength degradation under the earthquake of E2 level, which plays the role of structural fuse.
-
Key words:
- bridges /
- shear key /
- experiments /
- structural fuse concept /
- reconstruction /
- numerical simulation
-
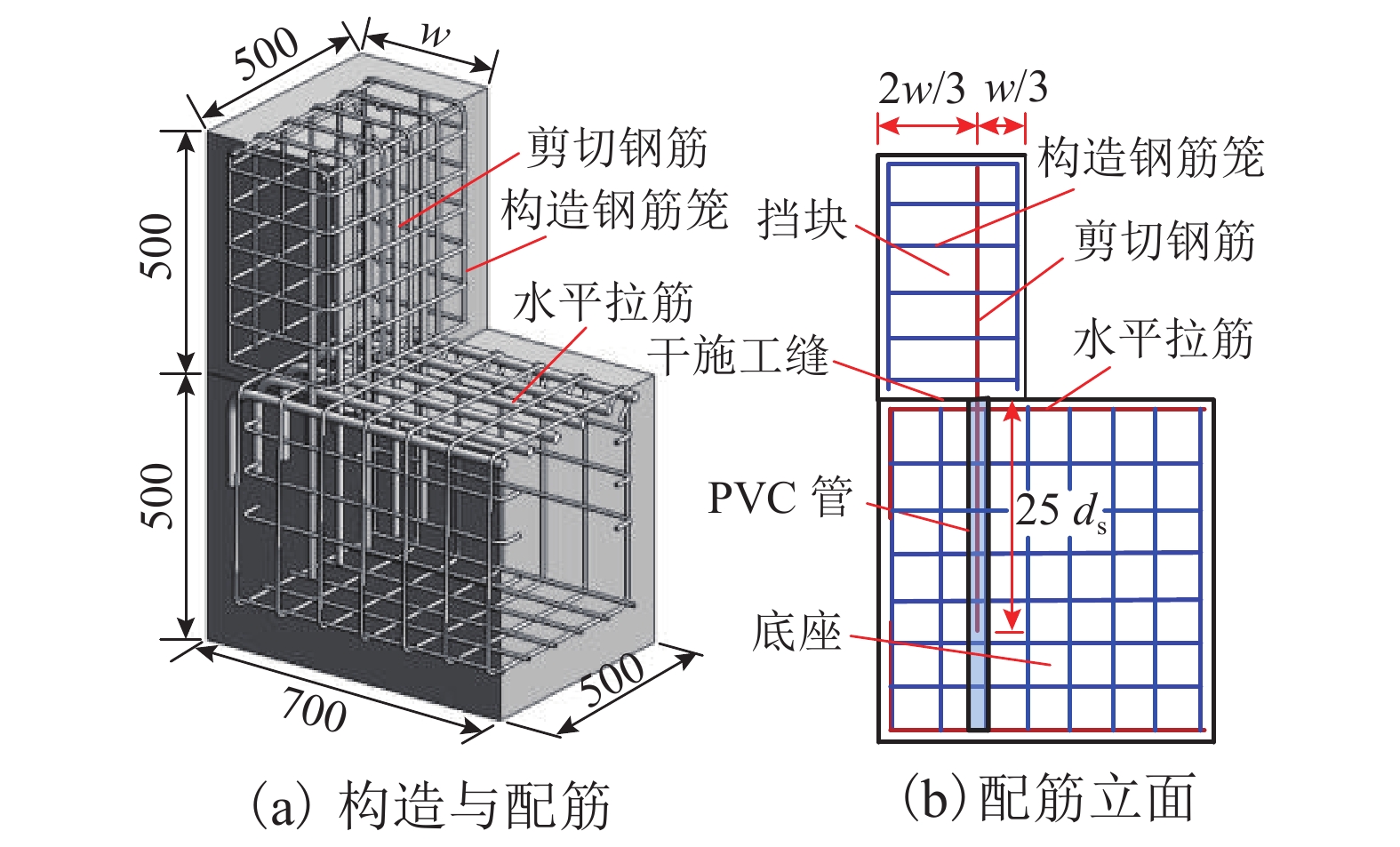
表 1 试件设计参数
Table 1. Design parameters of specimens
试件
编号混凝土
标号接触面
尺寸/mm剪切钢筋 底座拉筋 挡块预估
强度[7]/kN拉筋抗拉能力/
挡块预估强度1# C40 300 × 500 HRB400, 5 
12HRB400, 6 20423.6 2.04 2# C40 300 × 500 HRB400E, 5 12HRB400, 6 20411.5 2.10 3# C40 300 × 500 HRB400, 4 12HRB400, 6 20359.9 2.40 4# C50 300 × 500 HRB400, 5 12HRB400, 6 20423.6 2.04 5# C40 300 × 500 HRB400E, 3 12HRB400, 6 20288.9 2.99 6# C40 300 × 500 HRB400E, 2 20HRB400, 6 20446.2 1.94 7# C40 300 × 500 HRB400E, 3 16HRB400, 6 20428.0 2.02 8# C40 250 × 500 HRB400, 5 12HRB400, 6 20406.1 2.13 9# C40 350 × 500 HRB400, 5 12HRB400, 6 20441.1 1.96 10# C30 300 × 500 HRB400, 5 12HRB400, 6 20423.6 2.04 
下载: 导出CSV
表 2 试验结果与理论强度
Table 2. Test results and theoretical strengths
试件编号 混凝土强度/MPa 剪切钢筋强度/MPa 挡块实测
强度/kN滑移位移/
mm挡块理论
强度/kN误差/% 拉筋抗拉能力/
挡块实测强度底座 挡块 屈服 极限 1# 56.8 53.0 468 633 207.3 82 198.3 −4.35 4.17 2# 56.8 53.0 448 609 178.6 103 189.8 6.27 4.83 3# 56.8 53.0 468 633 152.1 75 158.6 4.29 5.68 4# 52.3 52.8 468 633 204.8 64 198.3 −3.18 4.22 5# 56.8 53.0 448 609 131.0 — 113.9 −13.07 6.59 6# 56.8 53.0 458 610 148.0 40 150.9 1.98 5.83 7# 56.8 53.0 448 602 155.7 69 151.8 −2.53 5.55 8# 56.8 53.0 468 633 136.2 32 198.3 45.58 6.34 9# 56.8 53.0 468 633 200.0 62 198.3 −0.86 4.32 10# 45.7 51.7 468 633 200.2 60 198.3 −0.96 4.31 注：混凝土和钢筋强度均按材料强度标准试验测得，4#的 C50 由于配比失误，实测强度与 C40 的实测强度接近；10个 试件均未加载至完全脱落，此处滑移位移指加载中最大实测值，5#是第 1 个探索性加载对象，未记录到滑移值.
下载: 导出CSV
-
重庆交通科研设计院. 公路桥梁抗震设计细则JTG/T B02-01—2008[S]. 北京: 人民交通出版社, 2008. 陈乐生, 庄卫林, 赵河清, 等. 汶川地震公路震害调查: 桥梁[M]. 北京: 人民交通出版社, 2012: 32-34. SILVA P F, MEGALLY S H, SEIBLE F. Seismic performance of sacrificial exterior shear keys in bridge abutments[J]. Earthquake Spectra, 2009, 25(3): 643-664. doi: 10.1193/1.3155405 VASSEGHI A. Energy dissipating shear key for precast concrete girder bridges[J]. Scientia Iranica, 2011, 18(3): 296-303. doi: 10.1016/j.scient.2011.05.036 邓开来,潘鹏,冉田苒,等. 耗能型桥梁抗震挡块试验研究[J]. 振动与冲击,2014,33(22): 7-12.DENG Kailai, PAN Peng, RAN Tianran, et al. Experimental study on energy dissipation stopper for bridge[J]. Journal of Vibration and Shock, 2014, 33(22): 7-12. 王克海, 惠迎新, 吴刚. 新型双层抗震挡块抗震性能研究[J]. 地震工程与工程振动, 2014, 34（增刊）: 505-510.WANG Kehai, HUI Yingxin, WU Gang. Study on seismic performance of seismic double-layer stopper[J]. Earthquake Engineering and Engineering Dynamics, 2014, 34（S）: 505-510. 徐略勤,李建中. 可牺牲抗震挡块的两水准设计方法[J]. 中国公路学报,2015,28(10): 59-66. doi: 10.3969/j.issn.1001-7372.2015.10.008XU Lueqin, LI Jianzhong. Dual-level design method of sacrificial aseismic retainers[J]. China Journal of Highway and Transport, 2015, 28(10): 59-66. doi: 10.3969/j.issn.1001-7372.2015.10.008 HAN Q, ZHOU Y L, OU Y C, et al. Seismic behavior of reinforced concrete sacrificial exterior shear keys of highway bridges[J]. Engineering Structures, 2017, 139(5): 59-70. XIANG N L, LI J Z. Seismic performance of highway bridges with different transverse unseating-prevention devices[J]. Journal of Bridge Engineering, 2016, 21(9): 1-16. 徐略勤,李建中. 新型滑移挡块的设计、试验及防震效果研究[J]. 工程力学,2016,33(2): 111-118.XU Lueqin, LI Jianzhong. Design and experimental investigation of a new type sliding retainer and its efficacy in seismic fortification[J]. Engineering Mechanics, 2016, 33(2): 111-118. CALTRANS. Caltrans seismic design criteria: version 1.7[S].California: California Department of Transportation, 2013. MEGALLY S H, SILVA P F, SEIBLE E F. Seismic response of sacrificial shear keys in bridge abutments[R]. San Diego: University of California at San Diego, 2001. BOZORGZADEH A, MEGALLY S H, ASHFORD S A, et al. Seismic response of sacrificial exterior shear keys in bridge abutments[R]. San Diego: University of California at San Diego, 2007. 阎西康,丛林,张玉淙. 不同植筋深度混凝土梁的静力试验研究[J]. 建筑科学,2016,32(11): 106-109.YAN Xikang, CONG Lin, ZHANG Yucong. Static tests on different planted depth of concrete beams[J]. Building Science, 2016, 32(11): 106-109. MAZZONI S, MCKENNA F, SCOTT M H, et al. Open system for earthquake engineering simulation: OpenSees command language manual[M]. Berkeley: Pacific Earthquake Engineering Center, 2007: 33-342. -
下载:
点击查看大图
图(10) / 表(2)
计量
- 文章访问数: 578
- HTML全文浏览量: 219
- PDF下载量: 16
- 被引次数: 0