Formation Mechanisim of Rail Corrugation Occurring on Tight Curved Track with Vanguard Fasteners
-
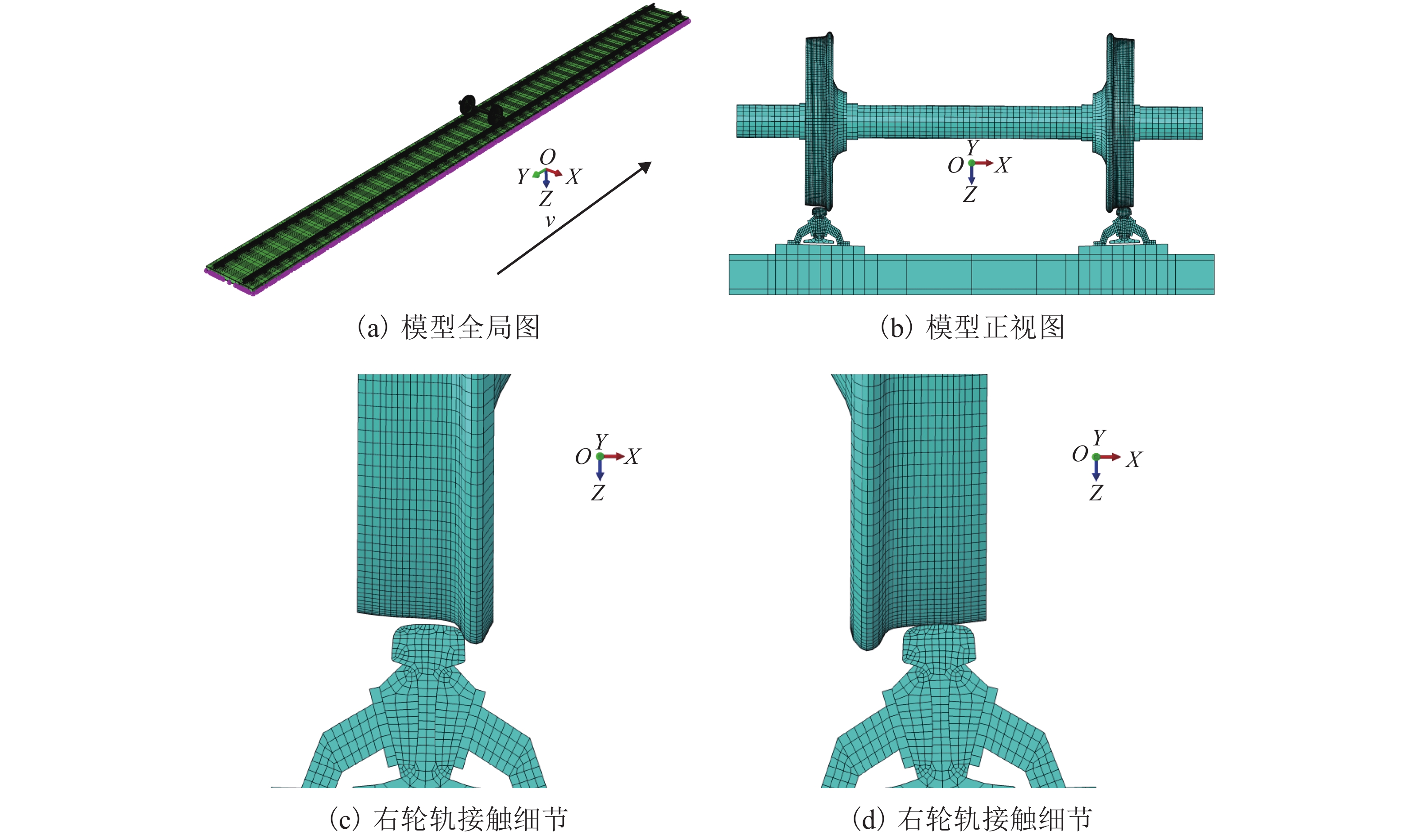
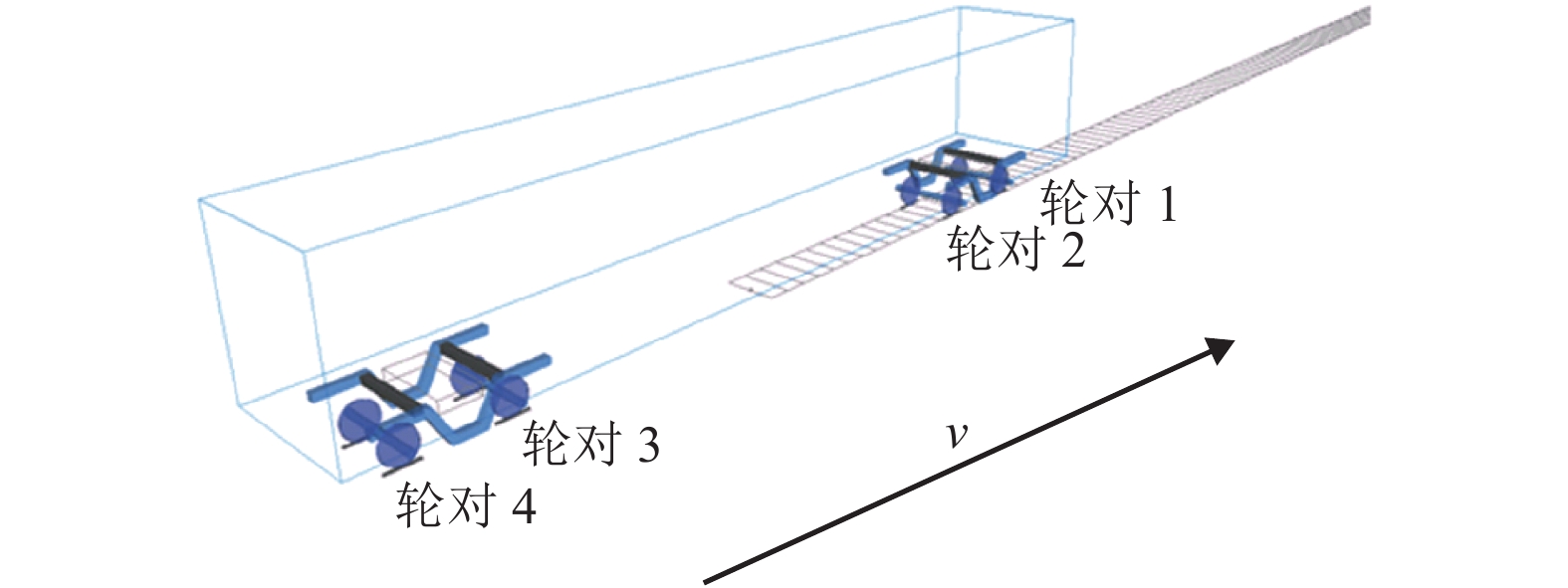
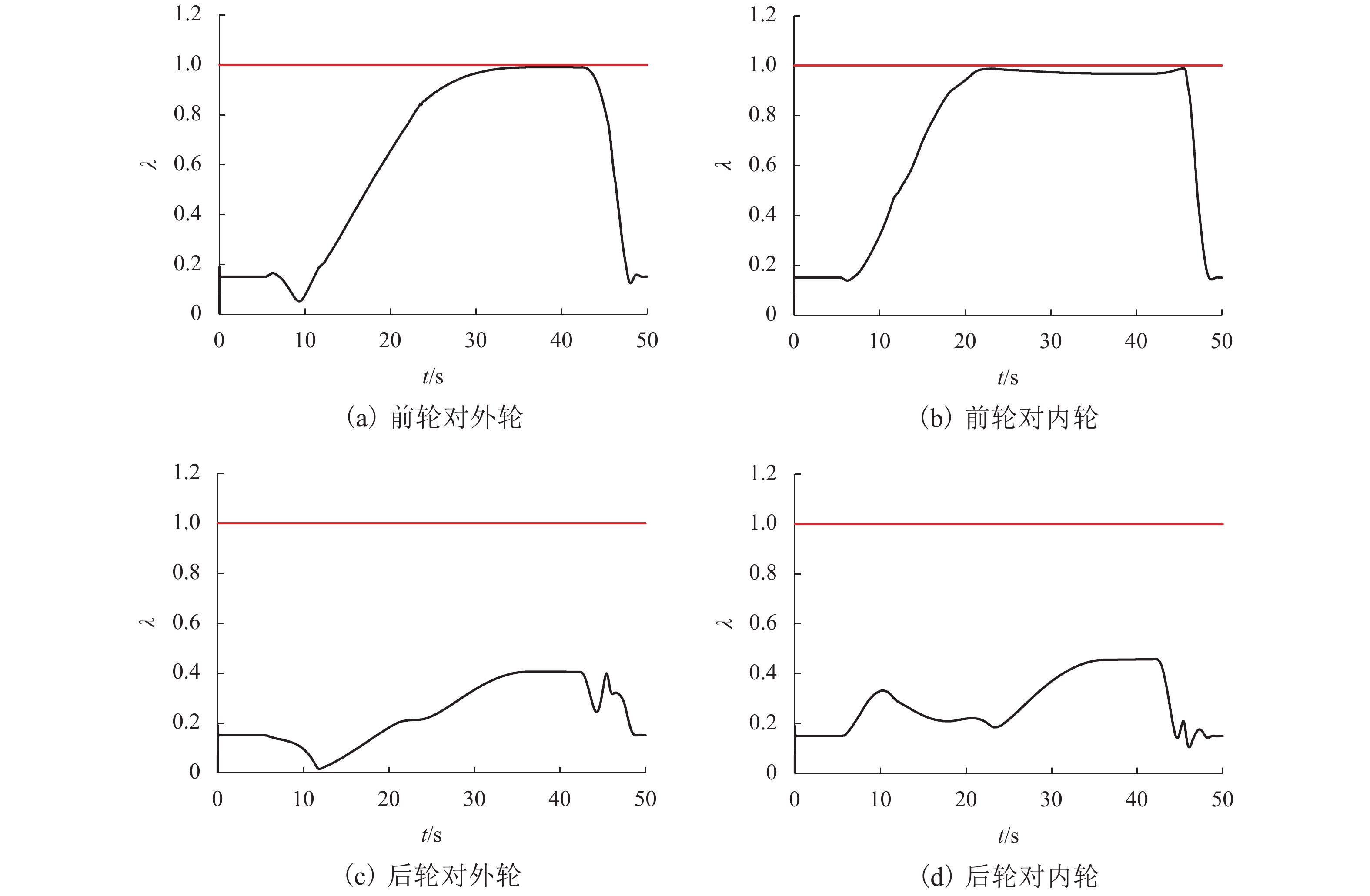
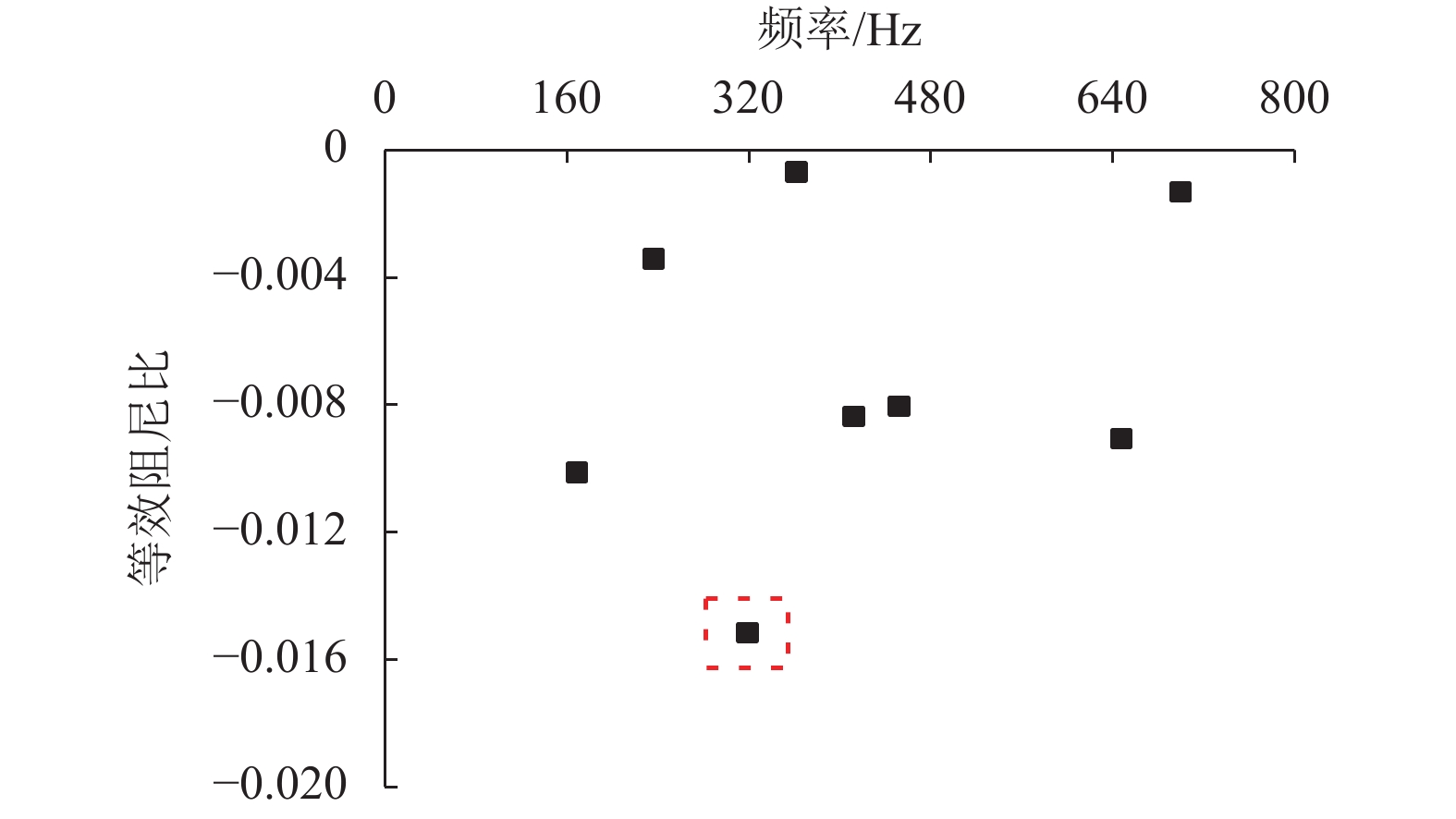
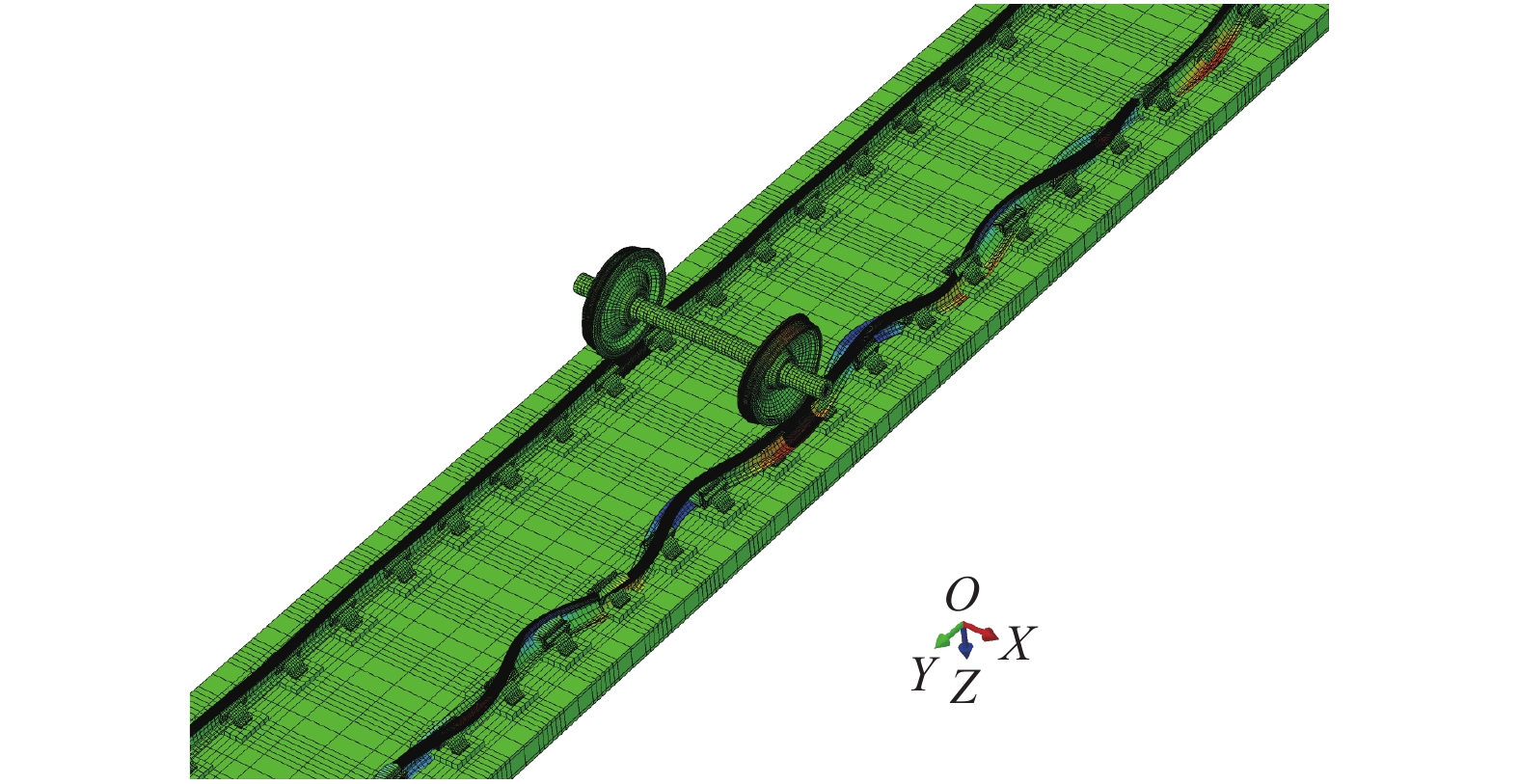
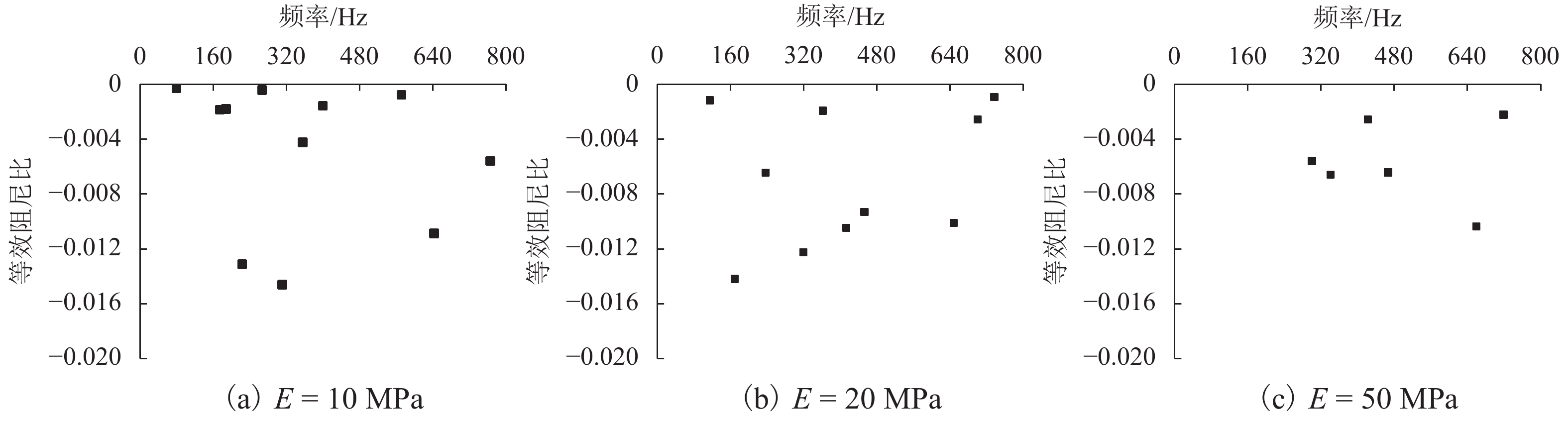
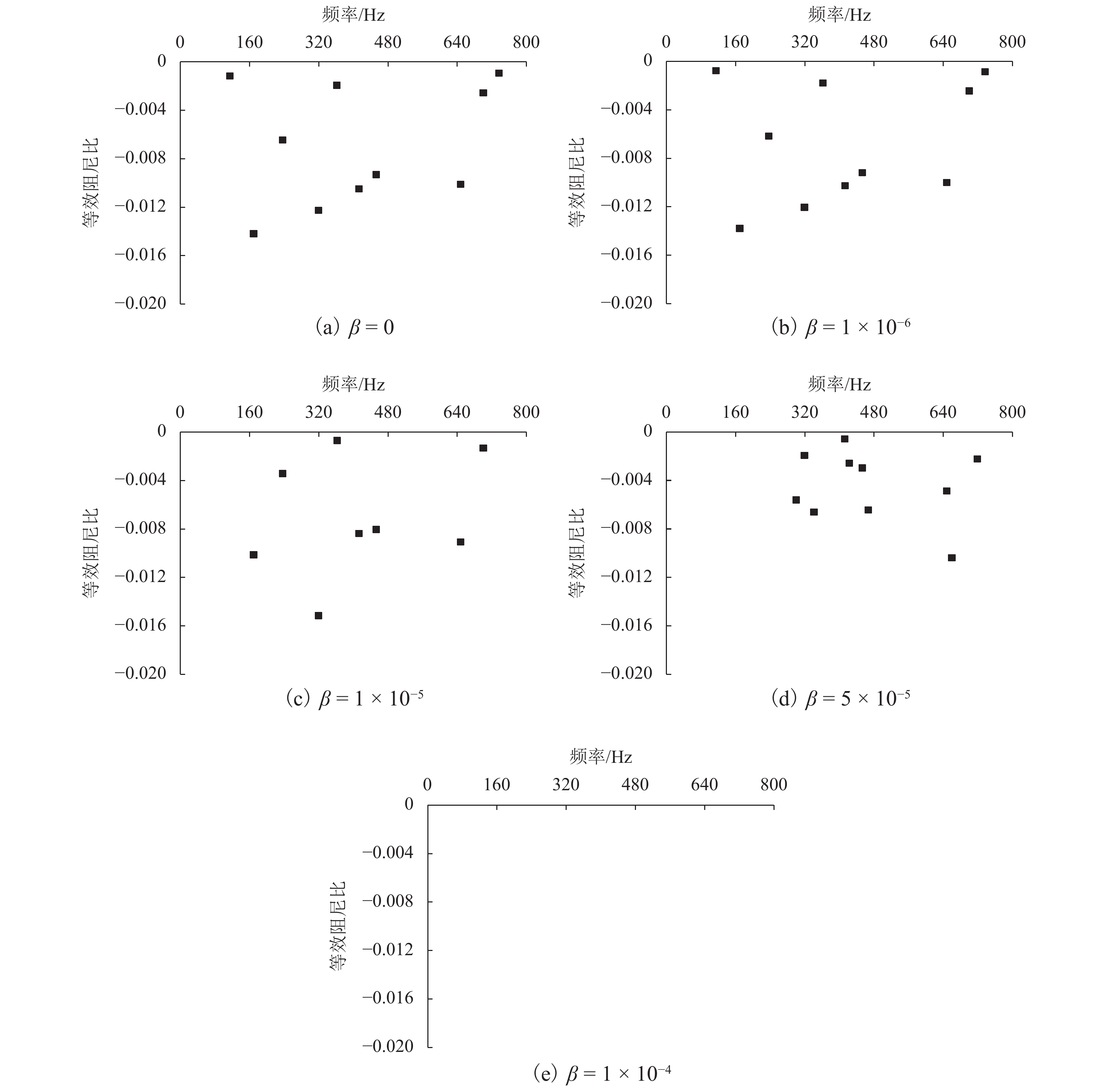
摘要: 为了研究先锋扣件地段钢轨波磨的成因并给出应对措施，基于摩擦自激振动引起钢轨波磨的理论，建立了包括导向轮对、轨道系统的自激振动有限元模型，使用复特征值法研究了轮对-轨道系统的动态稳定性；通过参数敏感性分析寻找影响钢轨波磨的主导因素，提出抑制乃至消除钢轨波磨的措施. 研究结果表明：轮轨间饱和的蠕滑力引起的轮对-轨道系统频率为319 Hz的自激振动是导致内侧钢轨严重的波磨的主要原因，模型预测的波磨波长为51.4 mm，与实测数据非常接近；参数敏感性分析表明，先锋扣件中的橡胶支承块的弹性模量和阻尼系数越大，钢轨波磨发生的可能性越低；采用弹性模量和阻尼系数有利于抑制乃至消除钢轨波磨，将阻尼系数提高到0.000 1可显著抑制钢轨波磨.Abstract: In order to study the formation mechanism and countermeasures of the rail corrugation on a tight curved track with vanguard fasteners. First, a self-excited vibration finite element model consisted of the leading wheelset and the track system was established based on the viewpoint of friction-induced vibration causing rail corrugation. The dynamic stability of the wheelset-track system was analyzed using the complex eigenvalue method. Then, the dominant factors affecting the rail corrugation were found through the parameter sensitivity analysis, and the countermeasures to suppress or eliminate the rail corrugation were put forward. The results show that the self-excited vibration of the wheelset-track system at 319 Hz induced by the saturated creep force between the wheel and the rail is the main cause of severe rail corrugation on the inner rail. The corrugation wavelength predicted by the model is 51.4 mm, which is closed to the measured data. The parameter sensitivity analysis shows that the modulus of elasticity and damping coefficient of the rubber rest pad in the vanguard fasteners have a great influence on the rail corrugation, the larger the elastic modulus and damping coefficient are, the lower the probability of rail corrugation occurrence is. The rubber rest pad with high modulus of elasticity and damping coefficient is beneficial to the suppression or even elimination of the rail corrugation. when the damping coefficient of the rubber rest pad is above 0.000 1, the rail corrugation can significantly be alleviated.
-
Key words:
- rail corrugation /
- friction-induced vibration /
- vanguard fasteners /
- wear /
- wheelset-track system
-
图 4 前转向架轮轨间的饱和蠕滑力
Figure 4. The saturated creep force between the wheels and rails of the front bogie
图 5 轮对-轨道系统的不稳定振动频率分布
Figure 5. The unstable vibration frequecies distribution of the wheelset-track system on a tighted curved track
图 6 轨道轮轨系统的不稳定振动振型
Figure 6. Mode shape of unstable vibration of the wheelset-track system on a tighted curved track
图 7 橡胶支承块弹性模量对轮-轨系统不稳定振动的影响
Figure 7. Effect of the modulus of elasticity of the rubber rest pad on the unstable vibration of the wheelset-track system
图 8 橡胶支承块阻尼系数对轮-轨系统不稳定振动的影响
Figure 8. Effect of the damping coefficient of the rubber rest pad on the unstable vibration of the wheelset-track system
表 1 轮轨系统的材料物理参数
Table 1. Material parameters of the wheelset-track system.
部件名称 密度 ρ/
（kg•m−3）弹性模量
E / MPa泊松比 阻尼
系数 ε轮对 7 800 210 000 0.30 − 钢轨 7 800 210 000 0.30 − 轨道板 2 400 32 400 0.24 − 侧板 7 800 200 000 0.30 − 橡胶
支承块900 20 0.40 1 × 10−5 
下载: 导出CSV
-
李伟,杜星,王衡禹,等. 地铁钢轨一种波磨机理的调查分析[J]. 机械工程学报,2013,49(16): 26-32. doi: 10.3901/JME.2013.16.026LI Wei, DU Xing, WANG Hengyu, et al. Investigation into the mechanism of type of rail corrugation of metro[J]. Journal of Mechanical Engineering, 2013, 49(16): 26-32. doi: 10.3901/JME.2013.16.026 仲莹涵,关庆华,温泽峰,等. 地铁钢轨波磨对轨道结构振动及减振特性影响[J]. 噪声与振动控制,2017,37(4): 85-89. doi: 10.3969/j.issn.1006-1355.2017.04.017ZHONG Yinghan, GUAN Qinghua, WEN Zefeng, et al. Influence of metro rail corrugation on track system ’s vibration and mitigation characteristics[J]. Noise and Vibration Control, 2017, 37(4): 85-89. doi: 10.3969/j.issn.1006-1355.2017.04.017 CUI X L, CHEN G X, YANG H G, et al. Study on rail corrugation of a metro tangential track with cologne-egg type fasteners[J]. Vehicle System Dynamics, 2016, 54(3): 353-369. doi: 10.1080/00423114.2015.1137955 ZHAO C, WANG P, SHENG X, et al. Theoretical simulation and experimental investigation of a rail damper to minimize short-pitch rail corrugation[J]. Mathematical Problems in Engineering, 2017, 4: 2359404.1-2359404.14. 崔晓璐,钱韦吉,张青,等. 直线线路科隆蛋扣件地段钢轨波磨成因的理论研究[J]. 振动与冲击,2016,35(13): 114-118,152.CUI Xiaolu, QIAN Weiji, ZHANG Qing, et al. Forming mechanism of rail corrugation of a straight track section supported by Cologne-egg fasteners[J]. Journal of Vibration and Shock, 2016, 35(13): 114-118,152. GRASSIE S L, KALOUSEK J. Rail corrugation:characteristics,causes and treatments[J]. Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit, 1993, 207(1): 57-68. doi: 10.1243/PIME_PROC_1993_207_227_02 JIN X, WEN Z, WANG K, et al. Effect of passenger car curving on rail corrugation at a curved track[J]. Wear, 2006, 260(6): 619-633. doi: 10.1016/j.wear.2005.03.016 BAEZA L, VILA P, XIE G, et al. Prediction of rail corrugation using a rotating flexible wheelset coupled with a flexible track model and a non-hertzian/non-steady contact model[J]. Journal of Sound and Vibration, 2011, 330(18/19): 4493-4507. doi: 10.1016/j.jsv.2011.03.032 CIAVARELLA M, BARBER J. Influence of longitudinal creepage and wheel inertia on short-pitch corrugation:a resonance-free mechanism to explain the roaring rail phenomenon[J]. Proceedings of the Institution of Mechanical Engineers,Part J:Journal of Engineering Tribology, 2008, 222(3): 171-181. doi: 10.1243/13506501JET373 WU T X, THOMPSON D J. An investigation into rail corrugation due to micro-slip under multiple wheel/rail interactions[J]. Wear, 2005, 258(7/8): 1115-1125. SUN Y Q, SIMSON S. Wagon-track modelling and parametric study on rail corrugation initiation due to wheel stick-slip process on curved track[J]. Wear, 2008, 265(9/10): 1193-1201. CHEN G X, ZHOU Z R, OUYANG H, et al. A finite element study on rail corrugation based on saturated creep force-induced self-excited vibration of a wheelset-track system[J]. Journal of Sound and Vibration, 2010, 329(22): 4643-4655. doi: 10.1016/j.jsv.2010.05.011 CUI X, CHEN G, ZHAO J, et al. Field investigation and numerical study of the rail corrugation caused by frictional self-excited vibration[J]. Wear, 2017, 376/377: 1919-1929. doi: 10.1016/j.wear.2017.01.089 CUI X, CHEN G, YANG H, et al. A case study of rail corrugation phenomenon based on the viewpoint of friction-induced oscillation of a wheelset-track system[J]. Journal of Vibroengineering, 2017, 19(6): 4516-4530. doi: 10.21595/jve.2017.17867 肖祥龙,陈光雄,莫继良,等. 摩擦调节剂抑制钢轨波磨的机理研究[J]. 振动与冲击,2013,32(8): 166-170. doi: 10.3969/j.issn.1000-3835.2013.08.029XIAO Xianglong, CHEN Guangxiong, MO Jiliang, et al. Mechanism for friction to suppress a wear-type rail corrugation[J]. Journal of Vibration and Shock, 2013, 32(8): 166-170. doi: 10.3969/j.issn.1000-3835.2013.08.029 QIAN W J, WU Y F, CHEN G X, et al. Experimental and numerical studies of the effects of a rail vibration absorber on suppressing short pitch rail corrugation[J]. Journal of Vibroengineering, 2016, 18(2): 1133-1144. CUI X L, CHEN G X, YANG H G, et al. Effect of the wheel/rail contact angle and the direction of the saturated creep force on rail corrugation[J]. Wear, 2015, 330/331: 554-562. doi: 10.1016/j.wear.2014.12.046 QIAN W J, CHEN G X, OUYANG H, et al. A transient dynamic study of the self-excited vibration of a railway wheel set-track system induced by saturated creep forces[J]. Vehicle System Dynamics, 2014, 52(9): 1115-1138. doi: 10.1080/00423114.2014.924629 BESHBICHI O E L. Complex eigenvalue analysis (CEA) and design of experiment analysis (DOE) towards the investigation of the interaction effects of track components on rail corrugation development[D]. Milano: Politecnico di Milano, 2017 LI W, WANG H, WEN Z, et al. An investigation into the mechanism of metro rail corrugation using experimental and theoretical methods[J]. Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit, 2016, 230(4): 1025-1039. doi: 10.1177/0954409715596182 BROCKLEY C A, KO P L. An investigation of rail corrugation using friction-induced vibration theory[J]. Wear, 1988, 128(1): 99-106. doi: 10.1016/0043-1648(88)90256-6 HIBBITT D, KARLSSON B, SORENSEN P. ABA-QUS Theory Manual[M/OL]. [2019-04-08]. https://max.book118.com/html/2017/0616/115969262.shtm OREGUI M, LI Z, DOLLEVOET R. An investigation into the modeling of railway fastening[J]. International Journal of Mechanical Sciences, 2015, 92: 1-11. doi: 10.1016/j.ijmecsci.2014.11.019 -
下载:
点击查看大图
图(8) / 表(1)
计量
- 文章访问数: 607
- HTML全文浏览量: 274
- PDF下载量: 22
- 被引次数: 0