Smoothness Estimation of Super-large Bridges in Railway Line Based on Fitting Railway Plane and Profile
-
摘要: 合理评价大跨度桥梁挠曲变形是保障桥上铁路行车平稳和舒适的基本前提. 针对当前大跨度桥梁挠曲变形重要评价指标挠跨比的不足，如忽略了挠曲变形对线路平纵断面的影响，本文基于桥梁挠曲变形曲线的规律以及铁路线路线型的特点，采用最小二乘法分别在平纵断面上将桥梁的挠曲变形曲线拟合成线路的标准线型，并依据铁路线路设计规范对其进行评价. 结合国内某特大桥的工程实例，研究发现：在考虑系统振动的最不利荷载工况下，该特大桥的最小竖曲线和平面曲线半径分别为29.3 km和54 km，符合规范要求；设置垂向预拱可以在一定程度上抵消桥梁竖向挠曲，有利于保持轨道结构的平顺性；本方法能从桥上线路平顺性的角度对桥梁的挠曲变形进行合理评价，可用于指导大跨度桥梁设计以保障铁路行车安全.Abstract: Reasonable evaluation of the flexural deformation of long-span bridges is the basic precondition of guaranteeing service stability and comfort of trains. Considering the limitations of the current evaluation index, the deflection-span ratio, such as the effects of deflection on railway plane and profile being ignored, a new methodology that uses the least-square method to fit the deformation curve into the standard railway line in plane and profile first and then evaluates the smoothness of railway super-large bridge by the Code for Design of Railway Line, was proposed. This method was applied to the engineering example of Wufeng Mountain super-large bridge for validation. Results show that under the worst load conditions of system vibration, the minimum radii of the vertical curve and plane circular curve are 29.3 km and 54 km, respectively, which conform to specification requirements. Setting up a vertical arch can neutralize the vertical deformation to some extent, and is beneficial to keep the regularity of track. The proposed method could evaluate the deformation of bridges properly from the aspect of railway smoothness and is applicable to instruct the design of long-span bridges and ensure the safety of railway operation.
-
Key words:
- long-span bridges /
- line smoothness /
- plane and profile /
- the least-square method
-
图 3 列车荷载作用下挠曲增加（包含预拱）与梁体曲率的变化规律
Figure 3. Relationship between bridge’s deflection (including the vertical arch) and beam curvature under train load
图 4 桥梁竖向挠曲与最小竖曲线半径关系
Figure 4. Relationship between bridge’s vertical deflection and minimum radius of vertical curve
图 6 横向风荷载作用下挠曲增加与梁体曲率变化规律
Figure 6. Relationship between bridge’s deflection and beam curvature under the lateral loads of wind
图 7 桥梁横向挠曲与最小平面曲线半径关系
Figure 7. Relationship between bridge’s lateral deflection and the minimum radius of plane curve
图 8 横向风荷载作用下桥梁平面曲线段拟合结果
Figure 8. Bridge’s plane curve fitting under the lateral loads of wind
表 1 竖曲线半径限值与挠曲变形峰值的关系
Table 1. Relationship between the limit value of vertical curve radius and the peak value of deflection
竖曲线半径/km 桥梁挠曲变形峰值（不设预拱）/m 桥梁挠曲变形峰值（设置预拱）/m 25 2.25 2.94 20 2.80 3.67 15 3.41 4.87 10 5.61 7.24 
下载: 导出CSV
表 2 竖曲线段评价结果
Table 2. Evaluation of vertical curve
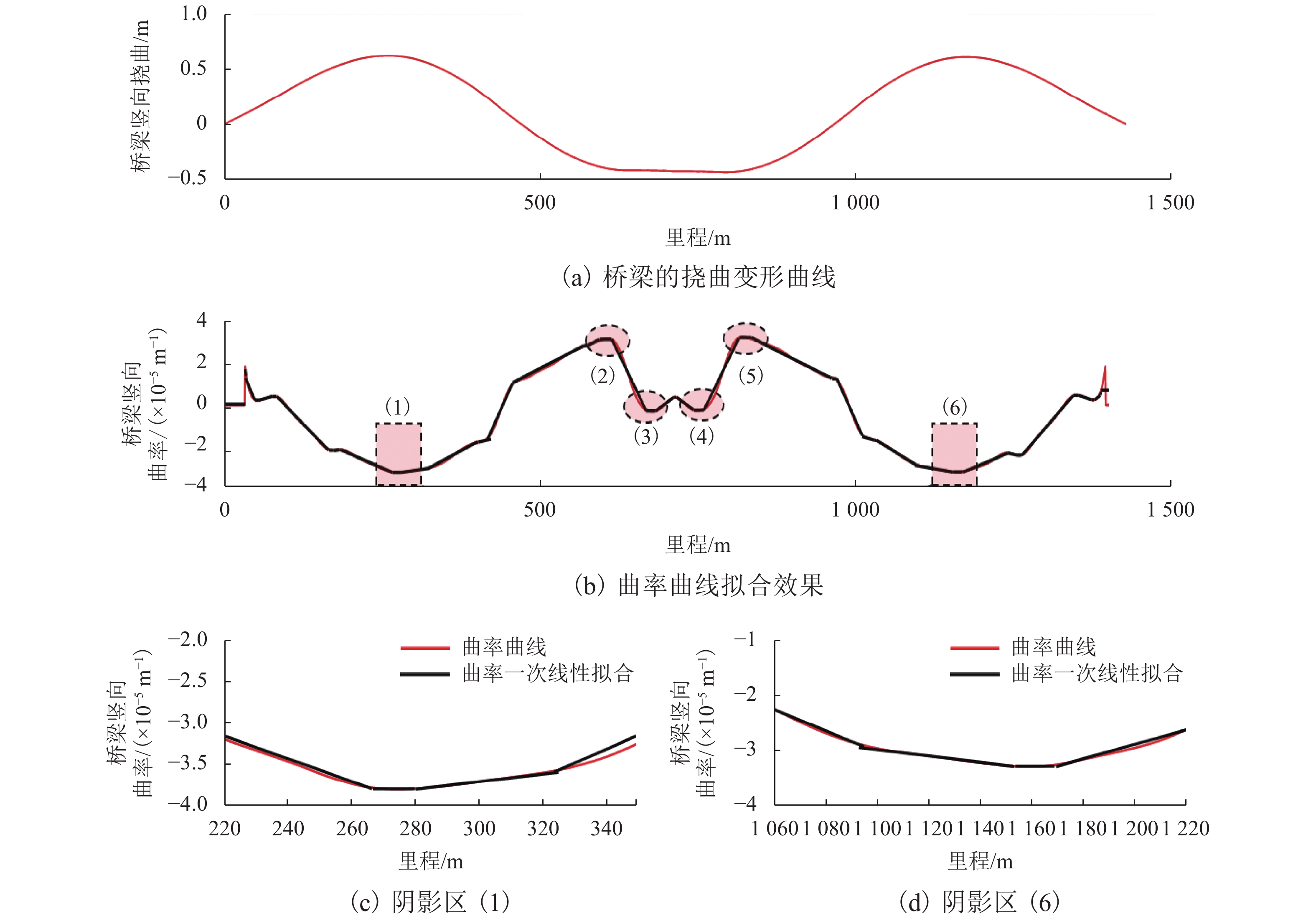
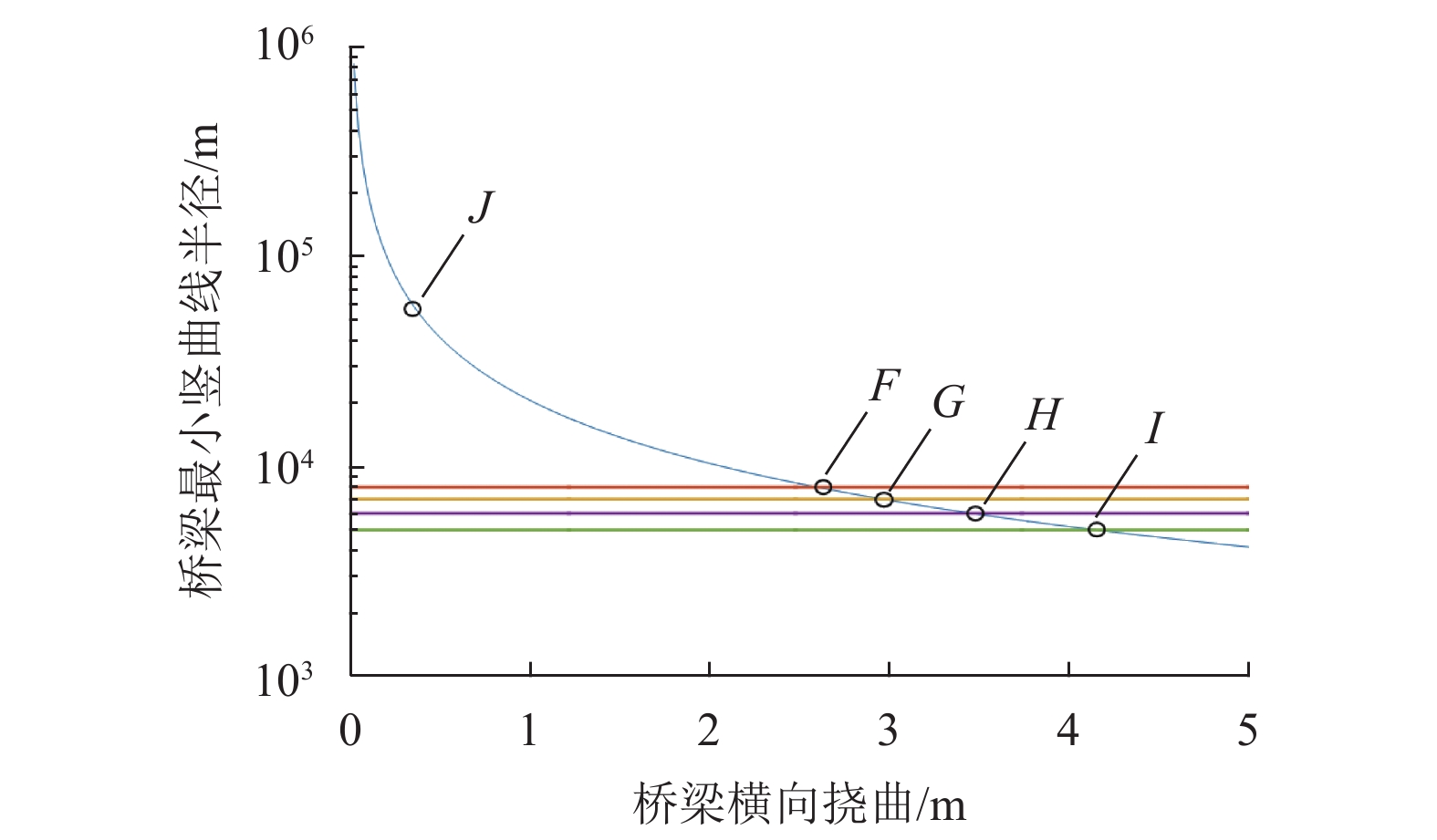
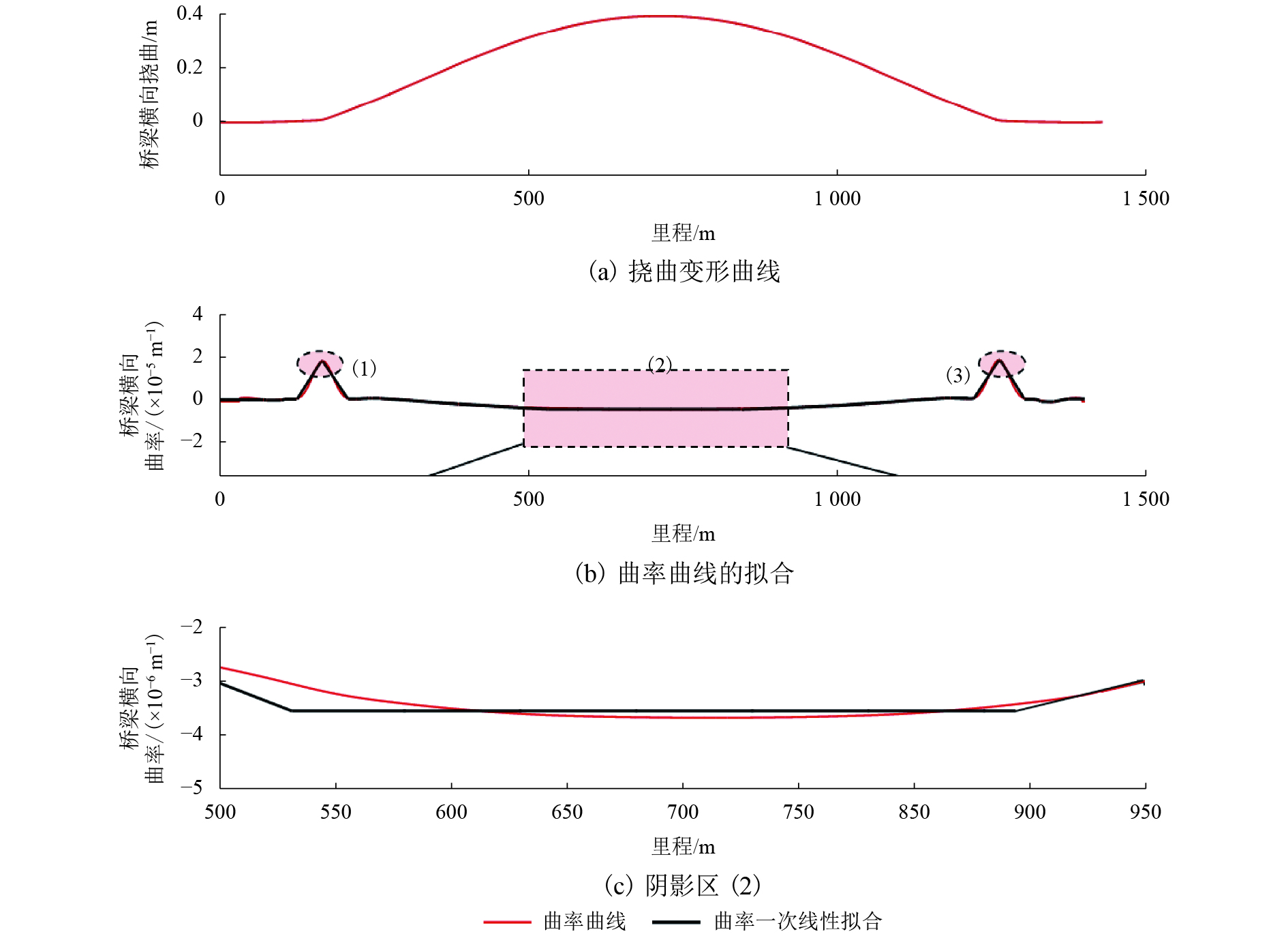
竖曲线（阴影区域） 曲线长度/m 曲率/(×10−5 m−1) 曲线半径/(×104 m) 半径规范最低限值/(×104 m) （1） 40 3.481 2.93 2.5 （2） 20 3.209 3.12 2.5 （3） 15 0.284 3.52 2.5 （4） 15 0.252 3.97 2.5 （5） 20 3.292 3.04 2.5 （6） 40 3.263 3.06 2.5
下载: 导出CSV
表 3 平面曲线段评价结果
Table 3. Evaluation of plane curve
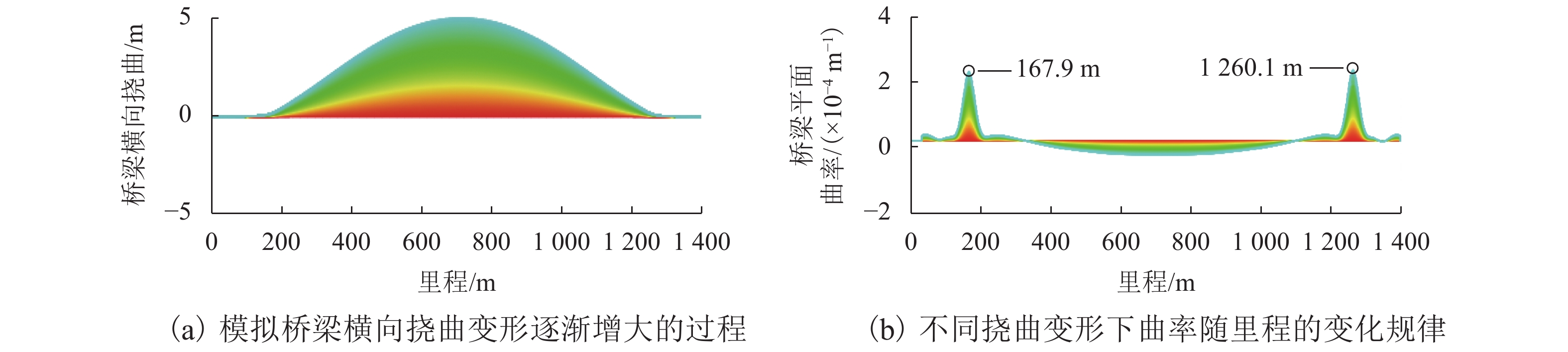
平面曲线（阴影区域） 曲线长度/m 曲率/(×10−5 m−1) 曲线半径/(× 104 m) 半径规范最低限值(× 104 m) (1) 10 1.839 5.4 0.7 (2) 350 −0.356 28.1 0.7 (3) 10 1.839 5.4 0.7
下载: 导出CSV
-
夏禾,徐幼麟. 大跨度悬索桥在风与列车荷载同时作用下的动力响应分析[J]. 铁道学报,2002,24(4): 83-91. doi: 10.3321/j.issn:1001-8360.2002.04.018XIA He, XU Youlin. Dynamic response of longspan suspension bridge to high wind and running train[J]. Journal of China Railway Society, 2002, 24(4): 83-91. doi: 10.3321/j.issn:1001-8360.2002.04.018 李永乐,蔡宪棠,安伟胜,等. 大跨度铁路悬索桥结构刚度敏感性研究[J]. 中国铁道科学,2011,32(4): 24-30.LI Yongle, CAI Xiantang, AN Weisheng, et al. Study on the sensitivity of the structural stiffness of long-span railway suspension bridge[J]. China Railway Science, 2011, 32(4): 24-30. CHATTERJEE P K, DATTA T K, SURANA C S. Vibration of continuous bridge under moving vehicles[J]. Journal of Sound and Vibration, 1994, 169(5): 619-632. doi: 10.1006/jsvi.1994.1037 MARCHESIELLO, FASANA, et al. Dynamic of multi-span continuous straight bridges subject to multi-degrees of freedom moving vehicle excitation[J]. Journal of Sound and Vibration, 1994, 224(3): 541-561. 李小珍,强士中,沈锐利. 高速列车-大跨度钢斜拉桥空间耦合振动响应研究[J]. 桥梁建设,1998(4): 67-70.LI Xiaozhen, QIANG Shizhong, SHEN Ruili. Studies on space dynamic responses of high speed train-long span steel cable-stayed bridge[J]. Bridge Construction, 1998(4): 67-70. 陈克坚,李永乐,李龙,等. 大跨度铁路钢桁梁斜拉桥刚度设计及取值研究[J]. 铁道工程学报,2014(3): 66-71. doi: 10.3969/j.issn.1006-2106.2014.03.012CHEN Kejian, LI Yongle, LI Long, et al. Research on the stiffness design and its value for long span railway steel truss cable-stayed bridge[J]. Journal of Railway Engineering Society, 2014(3): 66-71. doi: 10.3969/j.issn.1006-2106.2014.03.012 蔡宪棠. 大跨度铁路悬索桥刚度研究[D]. 成都: 西南交通大学, 2010. 王开云,吕凯凯. 高速铁路线路空间线形的动力学评价指标体系研究[J]. 西南交通大学学报,2016,51(2): 227-235. doi: 10.3969/j.issn.0258-2724.2016.02.002WANG Kaiyun, LÜ Kaikai. Dynamic evaluation index system for spatial alignment of high-speed railway[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 227-235. doi: 10.3969/j.issn.0258-2724.2016.02.002 翟婉明,王少林. 桥梁结构刚度对高速列车-轨道-桥梁耦合系统动力特性的影响[J]. 中国铁道科学,2012,33(1): 19-26. doi: 10.3969/j.issn.1001-4632.2012.01.04ZHAI Wanming, Wang Shaolin. Influence of bridge structure stiffness on the dynamics performance of high-speed train-track-bridge coupled system[J]. China Railway Science, 2012, 33(1): 19-26. doi: 10.3969/j.issn.1001-4632.2012.01.04 辛学忠,郭向荣. 大跨度铁路桥梁刚度统一描述方法探讨[J]. 铁道工程学报,2007(1): 82-86. doi: 10.3969/j.issn.1006-2106.2007.01.013XIN Xuezhong, GUO Xiangrong. Exploration on unified describing method for rigidity of large-span railway bridge[J]. Journal of Railway Engineering Society, 2007(1): 82-86. doi: 10.3969/j.issn.1006-2106.2007.01.013 赵会东,陈良江. 基于行车性能的大跨度高速铁路桥梁横向刚度控制指标研究[J]. 铁道建筑,2017,57(12): 1-4. doi: 10.3969/j.issn.1003-1995.2017.12.01ZHAO Huidong, CHEN Liangjiang. Research on limit values for lateral stiffness control of long span high speed railway bridges based on train operation performance[J]. Railway Engineering, 2017, 57(12): 1-4. doi: 10.3969/j.issn.1003-1995.2017.12.01 王海涌,党建武,王晓明. 基于舒适度的高速铁路线路设计与优化[J]. 铁道工程学报,2014,31(11): 31-34.WANG Haiyong, DANG Jianwu, WANG Xiaoming. Design and optimization of high-speed railway lines based on comfort[J]. Journal of Railway Engineering Society, 2014, 31(11): 31-34. PLCAKETT R L. The discovery of the least squares[J]. Biometrika, 1972, 59: 239-251. 田垅, 刘宗田. 最小二乘法分段直线拟合[J]. 计算机科学, 2012, 39(增刊1): 482-484.TIAN Long, LIU Zongtian. Least-squares method piecewise linear fitting[J]. Computer Science, 2012, 39(S1): 482-484. 李小珍,刘德军,晋智斌. 大跨度铁路悬索桥车-线-桥耦合振动分析[J]. 钢结构,2010,25(12): 6-12. doi: 10.3969/j.issn.1007-9963.2010.12.002LI Xiaozhen, LIU Dejun, JIN Zhibin. Analysis of train-track-bridge coupled vibration of a railway long-span suspension bridge[J]. Steel Construction, 2010, 25(12): 6-12. doi: 10.3969/j.issn.1007-9963.2010.12.002 -
下载:
点击查看大图
计量
- 文章访问数: 721
- HTML全文浏览量: 513
- PDF下载量: 83
- 被引次数: 0