Crack Detection of 3D Asphalt Pavement Based on Multi-feature Test
-
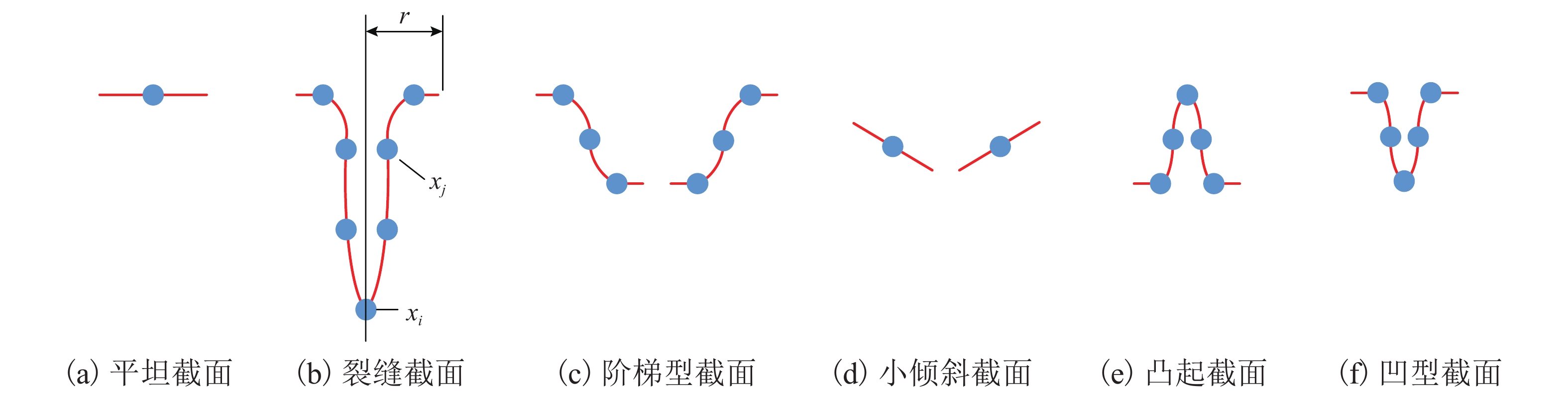
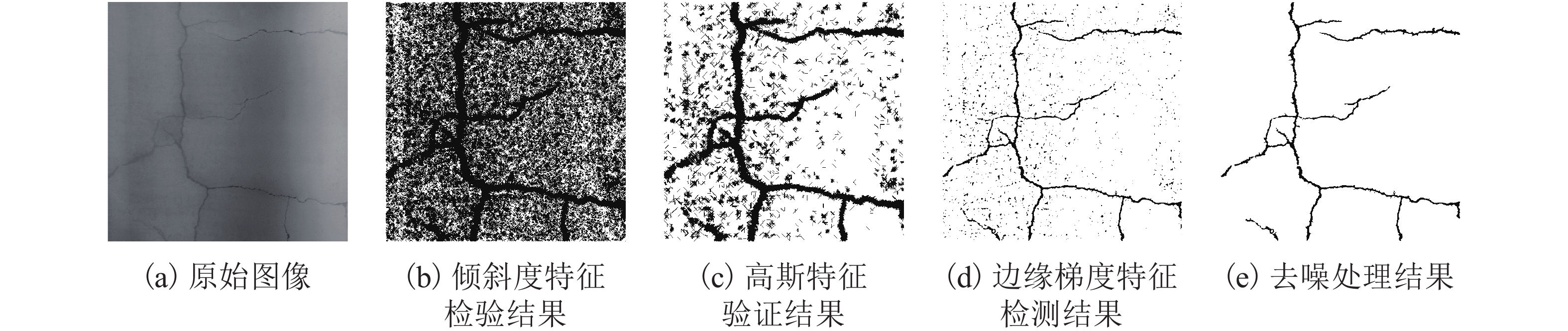
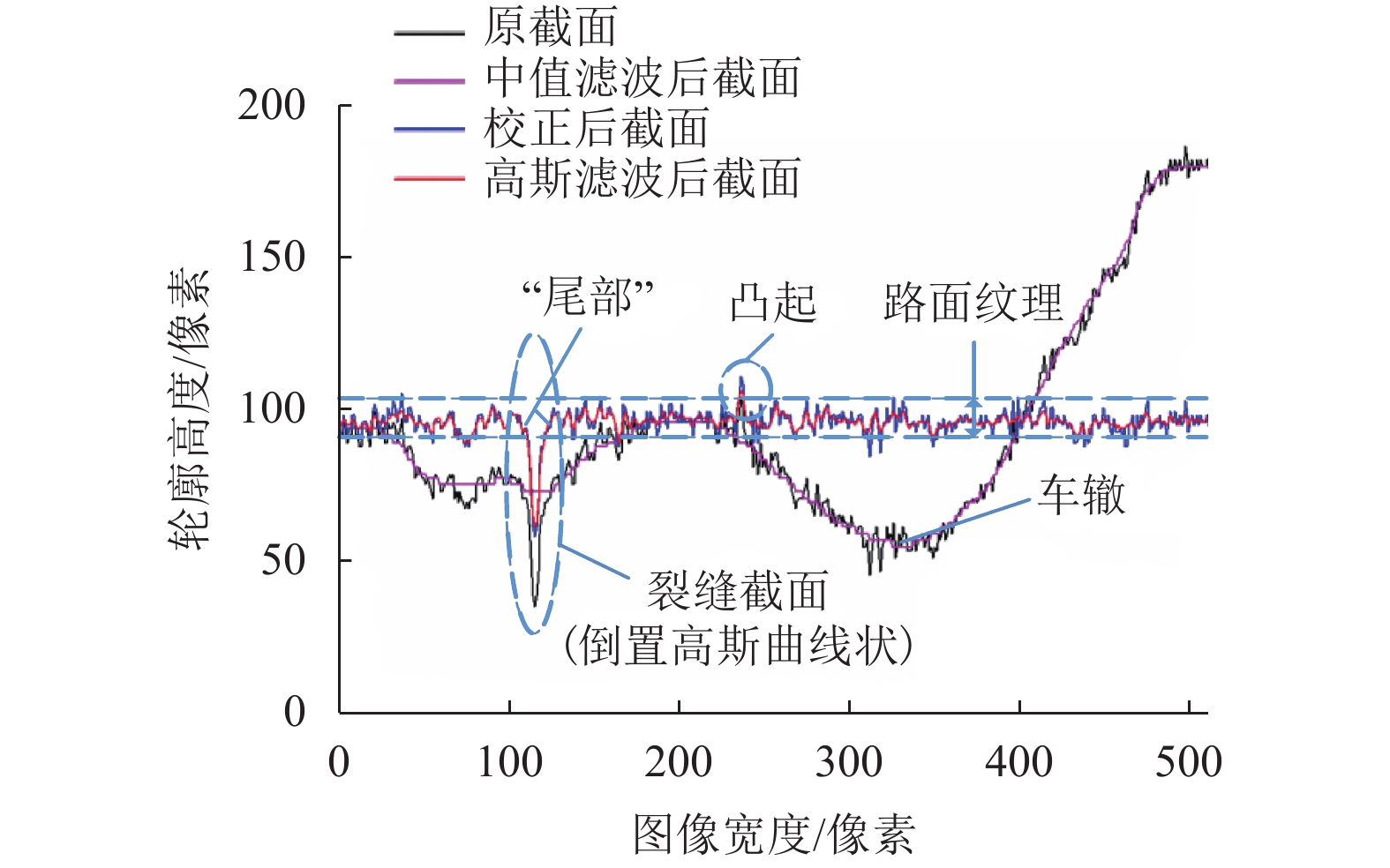
摘要: 针对由裂缝对比度低、路面纹理复杂多变等因素引起的沥青路面三维图像的裂缝检测精度低的问题，对原始三维裂缝图像进行尺寸降维、灰度校正、高斯滤波等预处理；然后以图像截面为研究对象，分别对4个方向的截面依次进行特别设计的倾斜度、高斯分布、边缘梯度3种特征检验，从而获得裂缝截面；接着对各个方向的裂缝截面进行融合和去噪，获得完整的裂缝二值图像；最后，根据路面粗糙度的高低，变化高斯分布特征检验中的相关参数，实现裂缝的高精度检测. 研究结果表明：提出的算法能达到89.19%的准确率、93.69%的召回率及91.06%的 F 值，优于基于三维光影、种子识别的典型三维图像裂缝检测方法.Abstract: In order to solve the accuracy problems in the crack detection of 3D asphalt pavement, which are mainly caused by low contrast between cracks and the surrounding area and complex pavement textures, a three-step preprocessing was conducted on original 3D images firstly, including size reducing, intensity correction and Gaussian smoothing. Then, three predominant feature tests of tilt-level, Gaussian-distribution and edge-gradient were applied to the image profiles of four directions successively so as to obtain the crack profiles. Moreover, the crack profiles of four directions were merged and denoised to acquire the intact cracks. Finally, according to the roughness of pavement surface, a related parameter in the Gaussian-distribution test was adjusted to realize the crack detection of high accuracy. The experiment result indicates that the proposed algorithm can reach 89.19% of accuracy, 93.69% of recall and 91.06% of F-measure, which outperforms another two typical 3D recognition algorithms based on the theories of 3D shadowing and crack seeds.
-
Key words:
- road engineering /
- detection algorithm /
- image processing /
- pavement cracking /
- multi-feature /
- 3D images
-
石材幕墙面板背栓式连接是石材幕墙的一种常见施工方法，采用背栓式连接的石材幕墙抗震性能力强[1-3]，稳定性能高[4-6]，施工强度低，机械化施工程度高，安装方便灵活. 石材幕墙连接节点的破坏占很大比例[7-8]，另外高温、湿度的变化都会导致石材强度下降[9]. 石材经风化后，承载力下降明显，石材幕墙面板常有断裂情况出现[10-11]，因此保证石材幕墙面板断裂后的整体性是提高面板安全性的重要措施. 目前，国内外关于石材幕墙面板加固和高空防坠措施的研究相对较少.
本文对33块背栓式石材面板进行了抗弯试验，并对其抗弯承载力进行了分析，研究了石材面板的加固和防高空坠落措施，为背栓式石材幕墙面板工程应用提供参考.
1. 试验概况
1.1 试件设计
石材面板为尺寸600 mm × 400 mm × 30 mm的花岗岩. 背栓采用慧鱼敲击式背栓，节点加固用不锈钢金属圆环，金属圆环厚度2 mm，金属圆环半径40 mm. 石材面板尺寸及加工方案见图1，试件的参数变化见表1. 试件编号中，BS、J、F、B分别表示背栓式石材面板、节点加固、迎风面加载、背风面加载，1、2、3、4分别代表GFRP （glass fiber reinforced plastics）布采用十字、对角、纵向全贴和横向全贴的加固方式. 所用石材均为同一批次黄金麻花岗岩.
考虑正负风压的作用，对石材面板进行了迎风面和背风面加载方向的试验，加载速度为0.5 mm/min，当荷载降至峰值荷载85%时停止加载，加载装置及测量方案如图2所示.
表 1 试件设计参数Table 1. Details of specimens试件编号 数量/个 厚度/mm 连接节点 GFRP 粘贴方式 试件编号 数量/个 厚度/mm 连接节点 GFRP 粘贴方式 BS-F 3 30 BS-B 3 30 BS-J-F 3 30 加固 BS-J-B 3 30 加固 BS-J-F-1 3 30 加固 十字 BS-J-B-1 3 30 加固 十字 BS-J-F-2 3 30 加固 对角 BS-J-B-2 3 30 加固 对角 BS-J-F-3 3 30 加固 纵向全贴 BS-J-B-3 3 30 加固 纵向全贴 BS-J-F-4 3 30 加固 横向全贴 1.2 材料性能
黄金麻花岗岩的实测弯曲强度为4.14 MPa. GFRP的实测性能如表2所示.
表 2 GFRP实测性能Table 2. Measured performance of GFRP试样 抗拉强度/MPa 厚度/mm 弹性模量/MPa GFRP 1 444.4 0.167 1.33 × 105 2. 试验结果
2.1 试验现象及破坏形态
在迎风面荷载作用下，石材面板标准件和节点加固的面板破坏时发出轻微的断裂声，面板断裂严重，承载力迅速下降，破坏非常突然. 背面采用GFRP十字粘贴和对角粘贴的石材幕墙面板，石材面板主要产生纵向贯通裂缝，加载过程中有GFRP的撕裂声，石材面板开裂后承载力缓慢下降，GFRP与断裂石材表面逐渐出现滑脱，破坏过程缓慢. 背面采用GFRP纵向和横向全贴的石材幕墙面板，破坏过程相似，分别出现纵向和横向贯通裂纹，承载力下降缓慢. 其破坏形态如图3（a）~（f）所示.
在背风面荷载的作用下，未进行加固的石材面板在背栓处产生了拉拔破坏现象，节点加固后的石材面板背栓孔处未发生破坏，说明采用金属圆环对石材面板连接节点进行加固是有效的. 背面采用GFRP加固的石材面板断裂后无碎块掉落，断裂石材与GFRP粘接完好，能保证一定的整体性. 其破坏形态如图3（g）~（k）所示.
2.2 试验结果与分析
不同试件极限荷载的柱状图如图4所示. 石材幕墙面板在不同荷载下的试验结果见表3所示，其中(1)、(2)、(3)表示在3次不同荷载下的试验.
表 3 不同荷载下试验结果Table 3. Test results under different loadings试件编号 试验 极限荷载/N 极限位移/mm 破坏形态 试件编号 试验 极限荷载/N 极限位移/mm 破坏形态 BS-F (1) 20.530 1.12 节点破坏 BS-B (1) 9.423 1.29 节点破坏 (2) 21.873 0.91 (2) 9.603 1.22 (3) 20.794 1.05 (3) 9.279 1.19 平均荷载 21.065 1.03 平均荷载 9.435 1.23 BS-J-F (1) 23.676 1.18 板断裂 BS-J-B (1) 14.051 1.91 板断裂 (2) 23.245 1.26 (2) 13.946 1.94 (3) 24.152 1.22 (3) 14.513 2.08 平均荷载 23.691 1.22 平均荷载 14.170 1.98 BS-J-F-1 (1) 69.533 5.03 板断裂 BS-J-B-1 (1) 14.867 1.63 板断裂 (2) 70.463 4.97 (2) 14.513 1.45 (3) 68.987 4.85 (3) 14.725 1.53 平均荷载 69.661 4.95 平均荷载 14.702 1.54 BS-J-F-2 (1) 58.765 4.22 板断裂 BS-J-B-2 (1) 16.478 1.32 板断裂 (2) 57.360 4.13 (2) 16.344 1.51 (3) 57.553 4.24 (3) 15.681 1.45 平均荷载 57.893 4.20 平均荷载 16.168 1.43 BS-J-F-3 (1) 31.113 1.43 板断裂 BS-J-B-3 (1) 14.862 1.29 板断裂 (2) 38.031 1.52 (2) 15.577 1.36 (3) 36.145 1.48 (3) 15.245 1.45 平均荷载 35.096 1.48 平均荷载 15.227 1.37 BS-J-F-4 (1) 56.975 2.71 板断裂 (2) 60.895 2.77 平均荷载 58.935 2.74 由表3可以看出：在迎风面加载作用下，背面采用十字、对角、纵向全贴和横向全贴GFRP进行加固石材面板，极限承载力分别是未加固石材面板的3.30倍、2.75倍、1.74倍和2.80倍. 试验采用的GFRP是单向编制的，GFRP粘贴方向对加固石材面板的极限承载力和破坏形态有一定影响. 两种全贴GFRP的加固方式下，石材断裂裂纹都出现在与纤维平行的方向，都没能充分发挥GFRP的强度.
在背风面加载条件下，节点加固石材面板的承载力是未加固试件的1.50倍，均为脆性破坏. 石材面板背面粘贴GFRP后，虽然承载力无明显提高，但是石材面板破坏后能保持整体性.
3. 有限元分析
3.1 有限元模拟校核
为了分析GFRP加固背栓式石材面板的受力过程，采用Abacus有限元软件对极限荷载进行了模拟. 将石材定为线弹性材料，采用最大主拉应力破坏准模拟开裂. 石材性能取实测性能，参考高强混凝土开裂应变经验值为1 × 10−4 [12]，石材的开裂应变取相同值. 石材实体单元用C3D8R减缩积分进行模拟，为了限制“沙漏”的扩展，直接选用enhanced方式控制沙漏.
假定纤维方向GFRP应力-应变关系为线弹性，用S4R壳单元来模拟. 材料本构关系和有限元本构模型分别如图5和图6所示. 图5中：σ和ε分别为石材的应力和应变；σu和εu分别为石材的极限压应力和极限压应变；σfe和εfe分别为GFRP的有效拉应力和有效拉应变. 石材面板与钢垫板设置表面与表面接触，接触属性定义为默认属性. 背栓与背栓孔的相互作用采用铰接约束.
模拟的结果与试验值进行对比如表4所示. 由表4可以看出，所建立的有限元模型基本正确，极限强度的误差在15.00%以内，可以用来分析GFRP加固石材幕墙面板的抗弯性能.
表 4 荷载模拟值与试验值对比Table 4. Comparison of simulated and experimental values试件编号 试验值/N 模拟值/N 误差/% BS-B 9 435.45 9 965.11 5.61 BS-J-B 14 170.55 15 383.55 8.56 BS-J-B-1 14 702.06 15 957.79 8.54 BS-J-B-2 16 168.12 17 680.88 9.36 BS-J-B-3 15 227.31 13 246.92 13.01 BS-F 21 065.81 23 706.66 12.54 BS-J-F-1 69 661.34 78 417.77 12.57 BS-J-F-2 57 893.21 64 527.76 11.46 BS-J-F-3 35 096.88 38 880.32 10.78 3.2 初始安装缺陷分析
背栓成孔质量对石材面板的受力有很大影响. 采用有限元模型可以分析背栓的初始安装缺陷对承载力的影响. 当背栓安装不合格时，认为该背栓不参与石材面板受力，其分析结果如表5所示.
表 5 初始安装缺陷分析Table 5. Initial installation defect analysis石材
编号缺陷数/个 极限荷载/N 试验荷载/N 降低率/% BS-B 1 6 382.3 9 435.0 32.36 BS-B 2 （对角） 4 229.7 9 435.0 55.17 由表5可以看出，背栓质量出现问题后，对背栓承载力影响很大，一个背栓开孔质量不合格，承载力下降约32.36%，出现两个不合格，则承载力下降达55.17%.
4. 结 论
1） 采用金属圆环对连接节点进行加固，对石材面板连接节点的承载力有明显的提高作用，相对于未加固的石材面板，承载力提高0.50倍.
2） 石材面板背面粘贴GFRP的3种加固方式，都能较好地保证石材面板破坏后的整体性，并能提高石材面板迎风面加载方向的抗弯承载力，十字粘贴效果较好，承载力提高2.30倍. 考虑到承载力的提高率以及材料用量的经济性，十字粘贴效果最好.
3） 有限元模型可以用来计算石材面板的承载力抗弯强度，计算误差在15.00%以内.
-
图 1 三维裂缝图像断面预处理实例
Figure 1. Illustration of a preprocessed profile in 3D asphalt pavement images
图 4 低粗糙度沥青路面裂缝检测结果对比
Figure 4. Comparison of crack detection using low textured asphalt pavement images
表 1 不同算法检测结果对比
Table 1. Comparison of crack detection using different methods
% 类型 图像编号 算法 A 算法 B 本文算法 准确率 召回率 F 值 准确率 召回率 F 值 准确率 召回率 F 值 低粗糙
度路面1～60 87.00 95.36 90.17 99.49 79.91 87.98 94.46 96.00 95.13 61～120 86.04 93.75 88.96 98.97 78.13 86.93 91.28 95.42 93.16 121～180 88.05 93.80 90.27 90.74 93.78 92.08 89.82 95.19 92.25 1～180 87.03 94.30 89.80 96.40 83.94 89.00 91.85 95.54 93.51 高粗糙
度路面181～240 54.34 94.65 66.90 93.42 88.63 90.68 89.61 92.30 90.68 241～300 48.59 94.97 62.33 93.06 88.06 90.37 87.98 91.20 89.27 301～360 55.68 90.48 65.86 90.42 71.62 78.71 81.97 92.00 85.88 181～360 52.87 93.37 65.03 92.30 82.77 86.59 86.52 91.83 88.61 汇总 1～360 69.95 93.84 77.42 94.35 83.36 87.80 89.19 93.69 91.06 
下载: 导出CSV
表 2 低粗糙程度沥青路面裂缝检测结果对比
Table 2. Comparison of crack detection using low textured asphalt pavement images
原始图象 人工批注 算法 A 算法 B 本文算法 
下载: 导出CSV
表 3 高粗糙程度沥青路面裂缝检测结果对比
Table 3. Comparison of crack detection using high textured asphalt pavement images
原始图象 人工批注 算法 A 算法 B 本文算法 
下载: 导出CSV
-
WANG K C P. Design and implementations of automated systems for pavement surface distress survey[J]. Journal of Infrastructure Systems, 2000, 6(1): 24-32. doi: 10.1061/(ASCE)1076-0342(2000)6:1(24) FUKUHARA T, TERADA K, NAGAO M, et al. Automatic pavement-distress-survey system[J]. Journal of Transportation Engineering, 1990, 116(3): 280-286. doi: 10.1061/(ASCE)0733-947X(1990)116:3(280) ZHANG P, LI H. Recognition of pavement surface crack[C]//Sixth International Conference on Natural Computation. Yantai: IEEE, 2010: 3393-3396. AYENU-PRAH A, ATTOH-OKINE N. Evaluating pavement cracks with bidimensional empirical mode decomposition[J]. Eurasip Journal on Advances in Signal Processing, 2008, 2008（1）: 861701.1-861701.7 NGUYEN T S, AVILA M, BEGOT S. Automatic detection and classification of defect on road pavement using anisotropy measure[C]//Signal Processing Conference. Glasgow: IEEE, 2009: 617-621. 彭博,WANG K C P,陈成,等. 基于各向异性测度的路面三维图像裂缝识别[J]. 西南交通大学学报,2014,49(5): 888-895. doi: 10.3969/j.issn.0258-2724.2014.05.023PENG Bo, WANG K C P, CHEN Cheng, et al. 3D pavement crack image detection based on anisotropy measure[J]. Journal of Southwest Jiaotong University, 2014, 49(5): 888-895. doi: 10.3969/j.issn.0258-2724.2014.05.023 CHENG H D, SHI X J, GLAZIER C. Real-time image thresholding based on sample space reduction and interpolation approach[J]. Journal of Computing in Civil Engineering, 2003, 17(4): 264-272. doi: 10.1061/(ASCE)0887-3801(2003)17:4(264) 王世芳,车艳丽,李楠,等. 一种基于多尺度脊边缘的沥青路面裂缝检测算法[J]. 中国公路学报,2017,30(4): 32-41. doi: 10.3969/j.issn.1001-7372.2017.04.005WANG Shifang, CHE Yanli, LI Nan, et al. Asphalt pavement crack detection algorithm based on multi-scale ridges[J]. China Journal of Highway and Transport, 2017, 30(4): 32-41. doi: 10.3969/j.issn.1001-7372.2017.04.005 ZOU Qin, CAO Yu, LI Qingquan, et al. CrackTree:automatic crack detection from pavement images[J]. Pattern Recognition Letters, 2012, 33(3): 227-238. doi: 10.1016/j.patrec.2011.11.004 WANG K C P. Elements of automated survey of pavements and a 3D methodology[J]. Journal of Modern Transportation, 2011, 19(1): 51-57. doi: 10.1007/BF03325740 TSAI Y C J, LI F. Critical assessment of detecting asphalt pavement cracks under different lighting and low intensity contrast conditions using emerging 3D laser technology[J]. Journal of Transportation Engineering, 2012, 138(5): 649-656. doi: 10.1061/(ASCE)TE.1943-5436.0000353 OUYANG W, XU B. Pavement cracking measurements using 3D laser-scan images[J]. Measurement Science & Technology, 2013, 24(10): 105204.1-105204.9. SOLLAZZO G, WANG K C P, BOSURGI G, et al. Hybrid procedure for automated detection of cracking with 3D pavement data[J]. Journal of Computing in Civil Engineering, 2016, 30(6): 04016032.1-04016032.12. doi: 10.1061/(ASCE)CP.1943-5487.0000597 JIANG C, TSAI Y J. Enhanced crack segmentation algorithm using 3D pavement data[J]. Journal of Computing in Civil Engineering, 2016, 30(3): 04015050.1-04015050.10. doi: 10.1061/(ASCE)CP.1943-5487.0000526 ZHANG A, WANG K C P, LI B, et al. Automated pixel-level pavement crack detection on 3D asphalt sur-faces using a deep-learning network[J]. Computer-Aided Civil and Infrastructure Engineering, 2017, 32(10): 805-819. doi: 10.1111/mice.12297 彭博. 基于路面高精三维图像的裂缝自动识别与分类算法[D]. 成都: 西南交通大学, 2014. FUJITA Y, HAMAMOTO Y. A robust automatic crack detection method from noisy concrete surfaces[J]. Machine Vision and Applications, 2011, 22(2): 245-254. doi: 10.1007/s00138-009-0244-5 SHAPIRO S, WILK M B. An analysis of variance test for normality (complete samples)[J]. Biometrika, 1965, 52: 591-611. doi: 10.1093/biomet/52.3-4.591 GUPTA S D, PATTANAYAK A K. Intelligent image analysis (IIA) using artificial neural network (ANN) for non-invasive estimation of chlorophyll content in micropropagated plants of potato[J]. In Vitro Cellular & Developmental Biology−Plant, 2017(14): 1-7. 彭博,WANG K C P,陈成,等. 基于1 mm精度路面三维图像的裂缝种子自动识别算法[J]. 中国公路学报,2014,27(12): 23-32. doi: 10.3969/j.issn.1001-7372.2014.12.004PENG Bo, WANG K C P, CHEN Cheng, et al. Automatic recognition for crack seeds based on 1 mm resolution 3D pavement images[J]. China Journal of Highway and Transport, 2014, 27(12): 23-32. doi: 10.3969/j.issn.1001-7372.2014.12.004 ZHNAG A, WANG K C P, AI C. 3D shadow modeling for detection of descended patterns on 3D pavement surface[J]. Journal of Computing in Civil Engineering, 2017, 31(4): 04017019.1-04017019.13. doi: 10.1061/(ASCE)CP.1943-5487.0000661 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 849
- HTML全文浏览量: 366
- PDF下载量: 50
- 被引次数: 0