基于复变函数理论的非圆形隧道解析解

李岩松; 陈寿根

doi:10.3969/j.issn.0258-2724.20180243

基于复变函数理论的非圆形隧道解析解

doi: 10.3969/j.issn.0258-2724.20180243

详细信息

作者简介:
李岩松（1989—），男，博士研究生，研究方向为隧道及岩石力学，E-mail：liyansong@my.swjtu.edu.cn

中图分类号: TU452
计量
- 文章访问数: 639
- HTML全文浏览量: 336
- PDF下载量: 30
- 被引次数: 0
出版历程
- 收稿日期: 2018-03-30
- 修回日期: 2018-07-23
- 网络出版日期: 2019-01-11
- 刊出日期: 2020-04-01

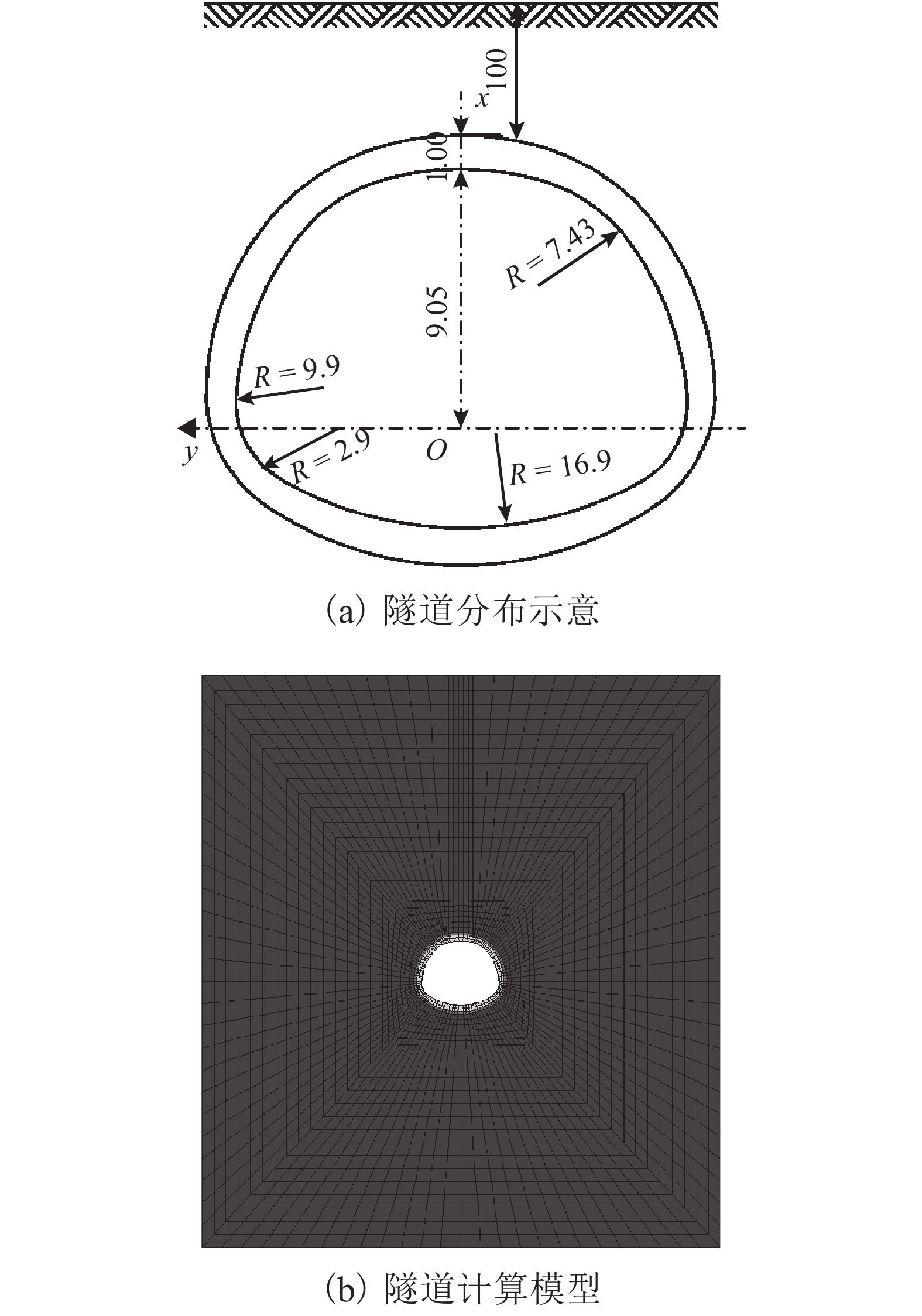
Lining and Surrounding Rock in Non-circular Tunnel Based on Complex Variable Method

摘要

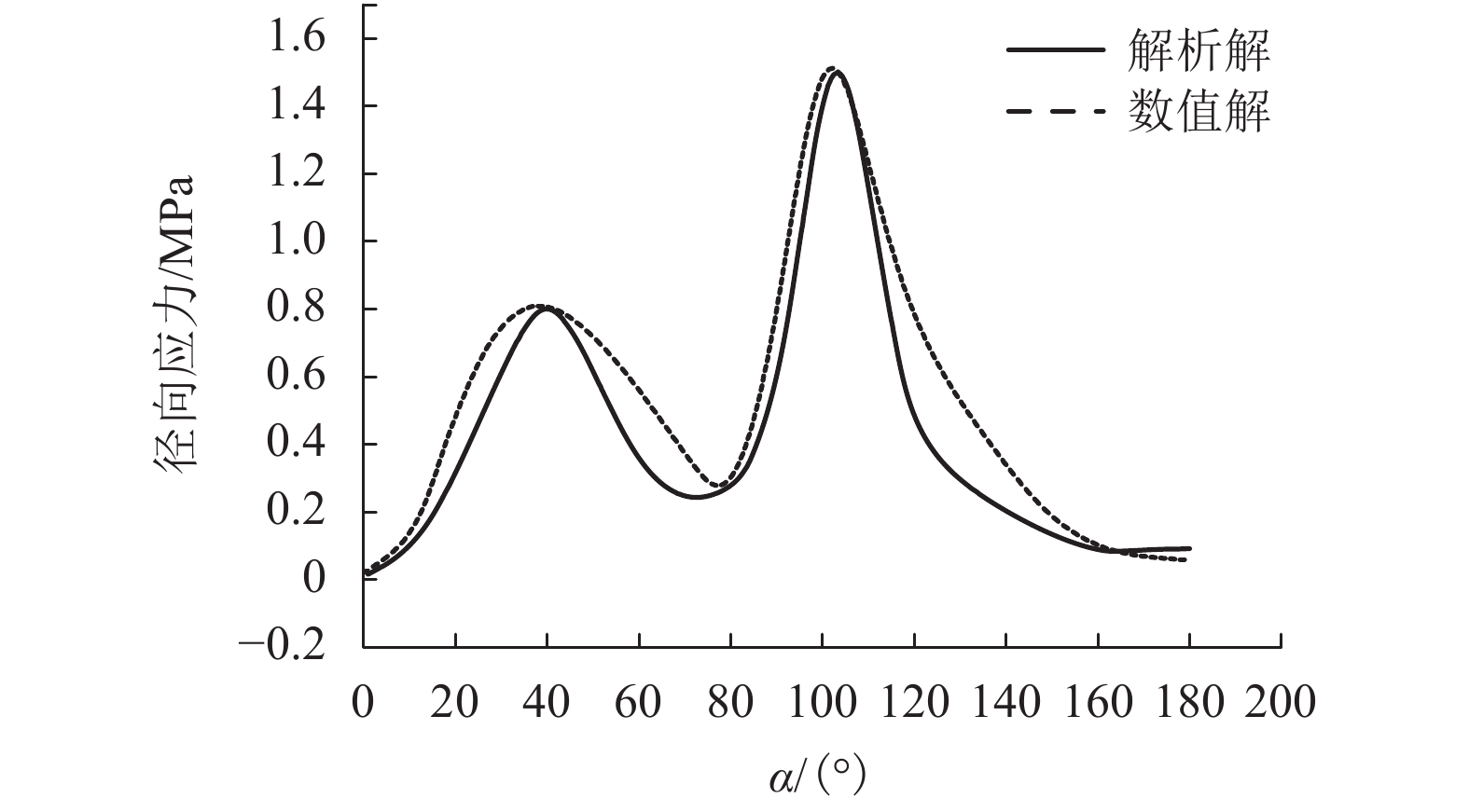
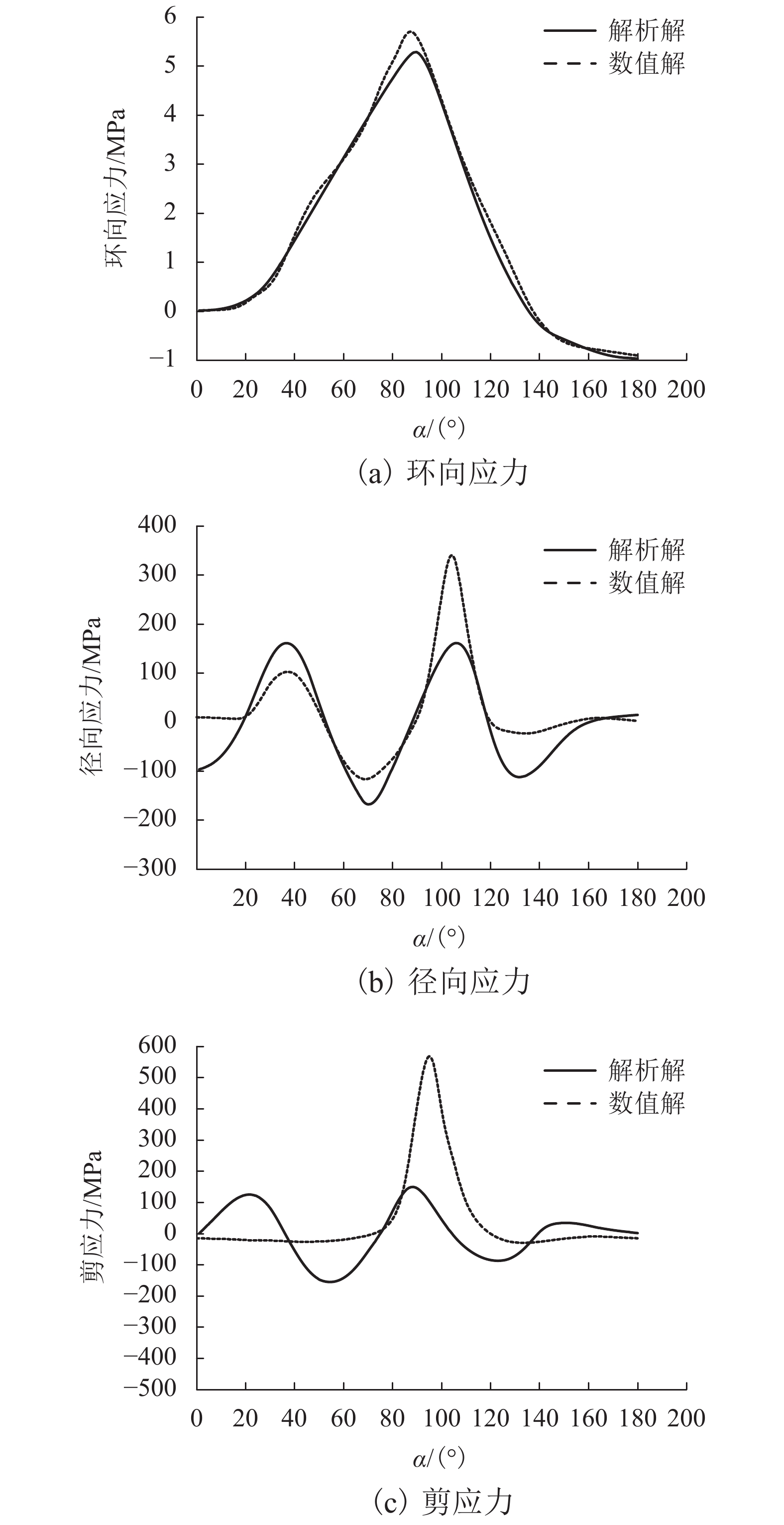
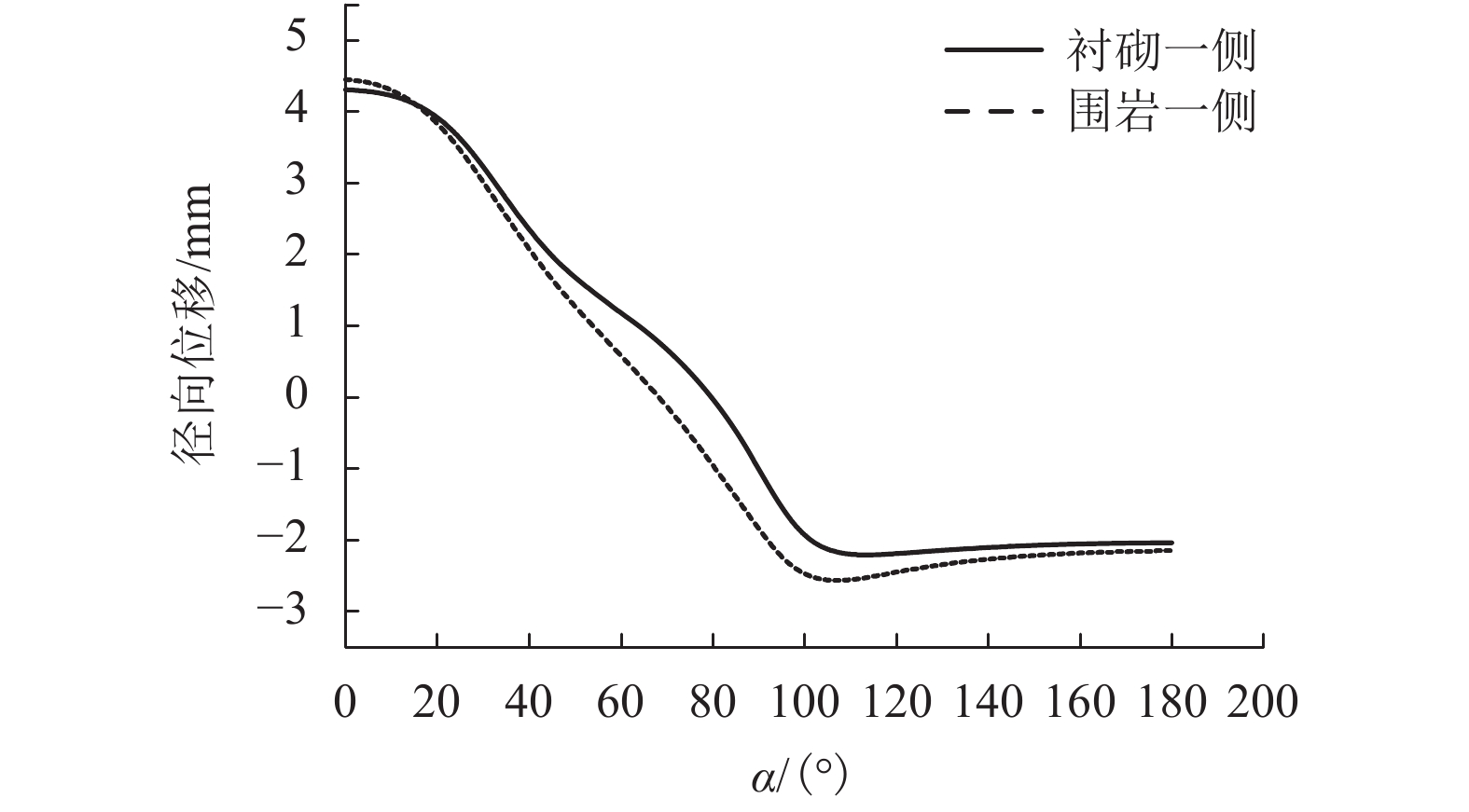
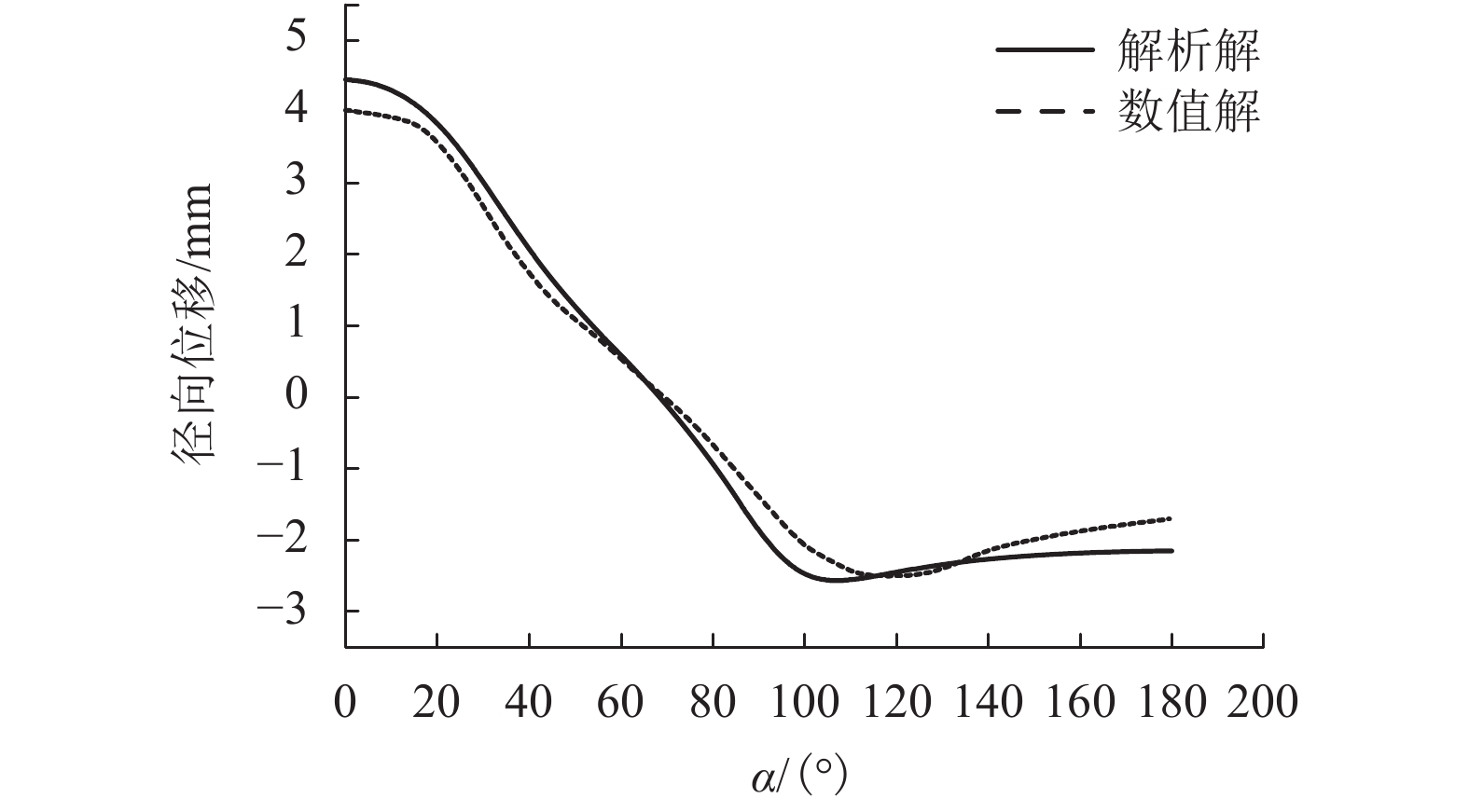
摘要: 为了得到考虑衬砌支护的非圆形隧道衬砌和围岩应力及变形的解析解，基于复变函数理论提出了一种求解考虑衬砌的非圆形隧道衬砌和围岩应力及变形的方法. 首先，为了克服非圆形隧道断面几何形状和考虑衬砌支护造成的计算困难问题，引入了保角变换，通过采取最优化解法确定映射函数中的各项系数，得到映射函数；其次，采用幂级数复变函数法克服隧道衬砌带来的多连通域问题，确定应力函数中的各项系数，建立方程求解；最后，通过Flac有限差分软件进行数值模拟证明解析解的正确性. 研究发现：弹性范围内解析解与Flac有限差分软件计算得到的应力、位移解有较好的吻合性，表明弹性解析法的结果是可靠、合理的；深埋条件下，弹性解析法无需根据埋深、工况建立计算模型，只需明确边界条件和映射函数就可计算非圆形隧道应力、位移，弹性解析法克服了计算软件在计算中由于网格划分尺寸等问题造成计算结果不精确、计算慢等问题，为非圆形隧道开挖问题提出了一种快速、准确的弹性计算方法.
- 非圆形隧道 /
- 衬砌 /
- 复变函数 /
- 弹性力学 /
- 数值模拟 /
- 解析解
Abstract: A complex variable method is presented of stress and displacement problems for a non-circular deep tunnel with a certain given boundary conditions at infinity. Firstly, in order to overcome the complex problems caused by non-circular geometric configurations and the lining supports, optimal design method are used to determine coefficients of the conformal mapping function. Secondly, The problem of the multiply connected region is overcome by Power series complex function method, which determine stress and displacement within tunnel lining and within surrounding rock. The coefficients in the stress functions are determined by complex variable method. Finally, the complex variable method is validated by FLAC finite difference software through an example. Both the complex variable method and the numerical simulation obtain the similar results of the stress concentration and the minimum radial displacement occurs at a similar place of tunnel. It is demonstrated that the complex variable complex variable method is reliable and reasonable. Under deep buried conditions, the complex variable method does not need to establish models and mesh according to different burial depth and working conditions. Only mapping function and boundary conditions are required for the calculation. The complex variable method overcomes the problems of inaccuracy and slow calculation caused by meshing dimension and other problems in software calculation. And it also provides another way for solving non-circular tunnel excavation problems in the range of elasticity in a fast and accurate way.
- non-circular tunnel /
- lining /
- complex variables /
- elasticity /
- numerical simulation /
- analytical solution

HTML全文

图 1 z平面保角变换为 ζ 平面示意

Figure 1. Conformal mapping of tunnel in z-plane in to two concentric circles in ζ-plane

下载: 全尺寸图片幻灯片

图 2 隧道计算简图（单位：m）

Figure 2. Tunnel calculation diagram (unit: m)

下载: 全尺寸图片幻灯片

图 3 衬砌与围岩接触面上环向应力

Figure 3. Circumferential stress along rock-lining interface

下载: 全尺寸图片幻灯片

图 4 衬砌与围岩接触面上径向应力

Figure 4. Normal stress along rock-lining interface

下载: 全尺寸图片幻灯片

图 5 衬砌与大气接触面上衬砌一侧应力

Figure 5. Stress along the inner lining periphery

下载: 全尺寸图片幻灯片

图 6 衬砌与围岩接触面上径向位移解析解

Figure 6. Radial displacement along rock-lining interface predicted by analytical solution

下载: 全尺寸图片幻灯片

图 7 衬砌与大气接触面上径向位移解

Figure 7. Radial displacement along inner lining periphery

下载: 全尺寸图片幻灯片

表 1 地层及材料参数

Table 1. Main physical parameter for tunnel calculation

名称弹性模
量/MPa 泊松比重度/
(kN•m⁻³) 侧压力
系数

板岩 25 000 0.3 26 0.5
衬砌 30 000 0.2 25 0.5

下载: 导出CSV

参考文献(24)

BOBET A. Analytical solutions for shallow tunnels in saturated ground[J]. Journal of Engineering Mechanics, 2001, 127: 1258-1266. doi: 10.1061/(ASCE)0733-9399(2001)127:12(1258)

BOBET A. Effect of pore water pressure on tunnel support during static and seismic loading[J]. Tunnelling Underground Space Technol, 2003, 18: 377-393. doi: 10.1016/S0886-7798(03)00008-7

LEE I M, NAM S W. The study of seepage forces acting on the tunnel lining and tunnel face in shallow tunnels[J]. Tunnelling Underground Space Technol, 2001, 16: 31-40. doi: 10.1016/S0886-7798(01)00028-1

TIMOSHENKO S P, GOODIER J. Theory of elasticity[J]. International Journal of Bulk Solids Storage Silos, 2011, 1: 567-567.

张治国,杨轩,宫剑飞,等. 复变函数法分析盾构隧道开挖引起的土体位移和衬砌变形[J]. 岩土工程学报,2017,39(9): 1626-1635. doi: 10.11779/CJGE201709010

ZHANG Zhiguo, YANG Xuan, GONG Jianfei, et al. A complex variable analysis of soil displacement and liner deformation induced by shield excavation[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(9): 1626-1635. doi: 10.11779/CJGE201709010

吴庆良,吕爱钟. 一类非均布荷载作用下厚壁圆筒平面问题的应力解析解[J]. 工程力学,2011,28(6): 6-18.

WU Qingliang, LÜ Aizhong. Stress analytical solution for plane problem of a thick-walled cylinder subjected to a type of non-uniform distributed pressures[J]. Engineering Mechanics, 2011, 28(6): 6-18.

高永涛,吴庆良,吕爱钟. 一类非均布荷载作用下双层厚壁圆筒光滑接触时的应力解析解[J]. 工程力学,2013,30(10): 93-99.

GAO Yongtao, WU Qingliang, LÜ Aizhong. Stress analytical solution a double-layered thick-walled cylinder with smooth contact interface subjected to a type of non-uniform distributed pressures[J]. Engineering Mechanics, 2013, 30(10): 93-99.

MUSKHELISHVILI N I, RADOK J R M. Some basic problems of the mathematical theory of elasticity[D]. [S.l.]: Cambridge University Press, 1953.

EXADAKTYLOS G E, STAVROPOULOU M C. A closed-form elastic solution for stresses and displacements around tunnels[J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39: 905-916.

EXADAKTYLOS G E, LIOLIO P A, STAVROPOULOU M C. A semi-analytical elastic stress displacement solution for notched circular openings in rocks[J]. International Journal of Solids and Structures, 2003, 40: 1165-1187. doi: 10.1016/S0020-7683(02)00646-7

VERRUIJT A. A complex variable solution for a deforming circular tunnel in an elastic half-plane[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 21: 77-89. doi: 10.1002/(SICI)1096-9853(199702)21:2<77::AID-NAG857>3.0.CO;2-M

VERRUIJT A. Deformations of an elastic half plane with a circular cavity[J]. International Journal of Solids and Structures, 1998, 35(21): 2795-2804. doi: 10.1016/S0020-7683(97)00194-7

ZHAO Guangpu, Yang Shengli. Analytical solutions for rock stress around square tunnels using complex variable theory[J]. International Journal of Rock Mechanics & Mining Sciences, 2015, 80: 302-307.

KARGAR A R, RAHMANNEJAD R, HAJABASI M A. A semi-analytical elastic solution for stress field of lined non-circular tunnels at great depth using complex variable method[J]. International Journal of Solids and Structures, 2014, 51: 1475-1482. doi: 10.1016/j.ijsolstr.2013.12.038

LÜ Aizhong, ZHANG Ning, LIN Kuang. Analytic solutions of stress and displacement for a non-circular tunnel at great depth including support delay[J]. International Journal of Rock Mechanics & Mining Sciences, 2014, 70: 69-81.

LÜ Aizhong, ZHANG Ning, QIN Yuan. Analytical solutions for the stress of a lined non-circular tunnel under full-slip contact conditions[J]. International Journal of Rock Mechanics & Mining Sciences, 2015, 79: 183-192.

邓涛,魏雯,关振长,等. 公路隧道开挖问题的复变函数解及应用[J]. 中国公路学报,2015,28(10): 90-97. doi: 10.3969/j.issn.1001-7372.2015.10.012

DENG Tao, WEI, Wen, GUAN Zhenchang, et al. Complex variable function solution and its application[J]. China Journal of Highway and Transport, 2015, 28(10): 90-97. doi: 10.3969/j.issn.1001-7372.2015.10.012

刘福胜. 基于流固耦合及复变函数分析的隧道渗流问题研究[D]. 广州: 华南理工大学, 2012.

王光钦. 弹性力学[M]. 北京: 中国铁道出版社, 2008: 256.

陈子荫. 围岩力学分析中的解析方法[M]. 北京: 煤炭工业出版社, 1994.

吕爱钟, 张路青. 地下隧洞力学分析的复变函数方法[M]. 北京: 科学出版社, 2007: 94.

詹姆斯·沃德·布朗, 鲁埃尔V. 丘吉尔. 复变函数及其应用[M]. 北京: 机械工业出版社, 2015: 30-34.

杜朝伟,王梦恕,谭忠盛. 水下隧道渗流场解析解及其应用[J]. 岩石力学与工程学报,2011,30(2): 3568-3573.

DU Chaowei, WANG Mengshu, TAN Zhongsheng. Analytic solution for seepage field of subsea tunnel and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 3568-3573.

吕爱钟,陈虹宇,覃媛,等. 光滑接触条件下隧洞支护断面形状优化[J]. 岩石力学与工程学报,2015,33(8): 1563-1571.

LÜ Aizhong, CHEN Hongyu, TAN Yuan, et al. Shape optimization of tunnel support section under contact condition of pure slip[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 33(8): 1563-1571.

施引文献

附加材料(0)

访问统计