Bubble Model Based Grid Generation and Grid Size Control over Free-Form Surface
-
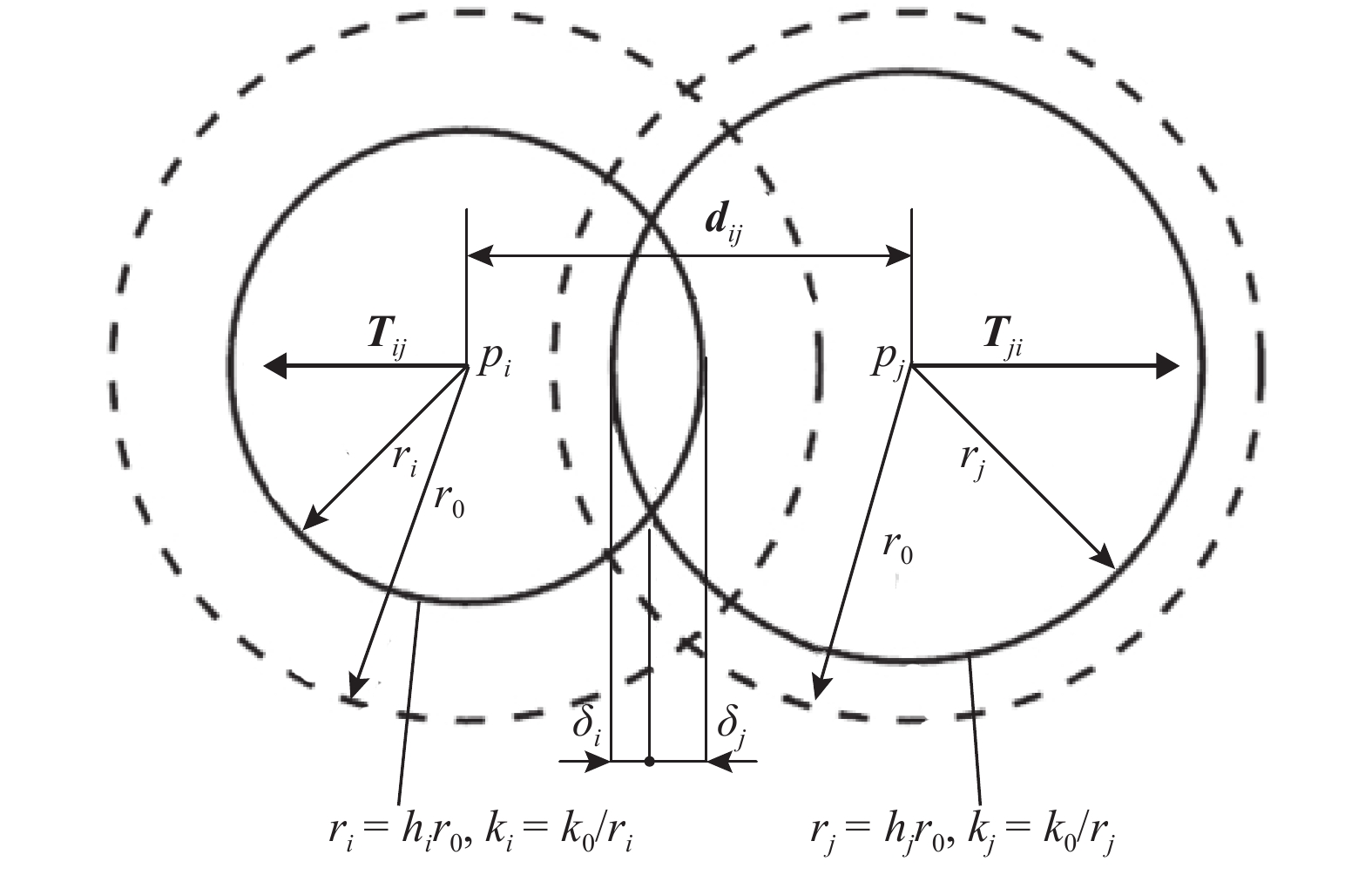
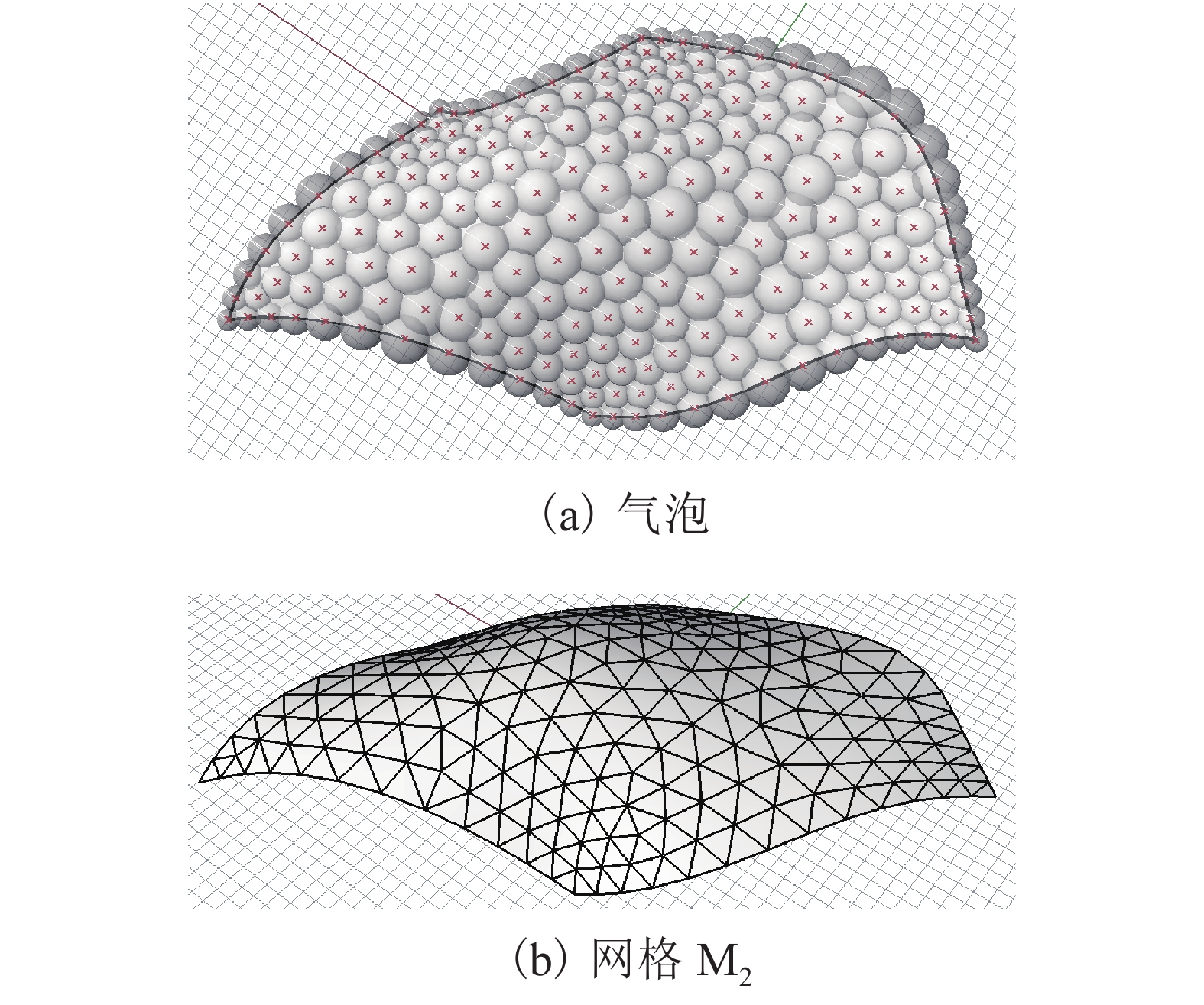
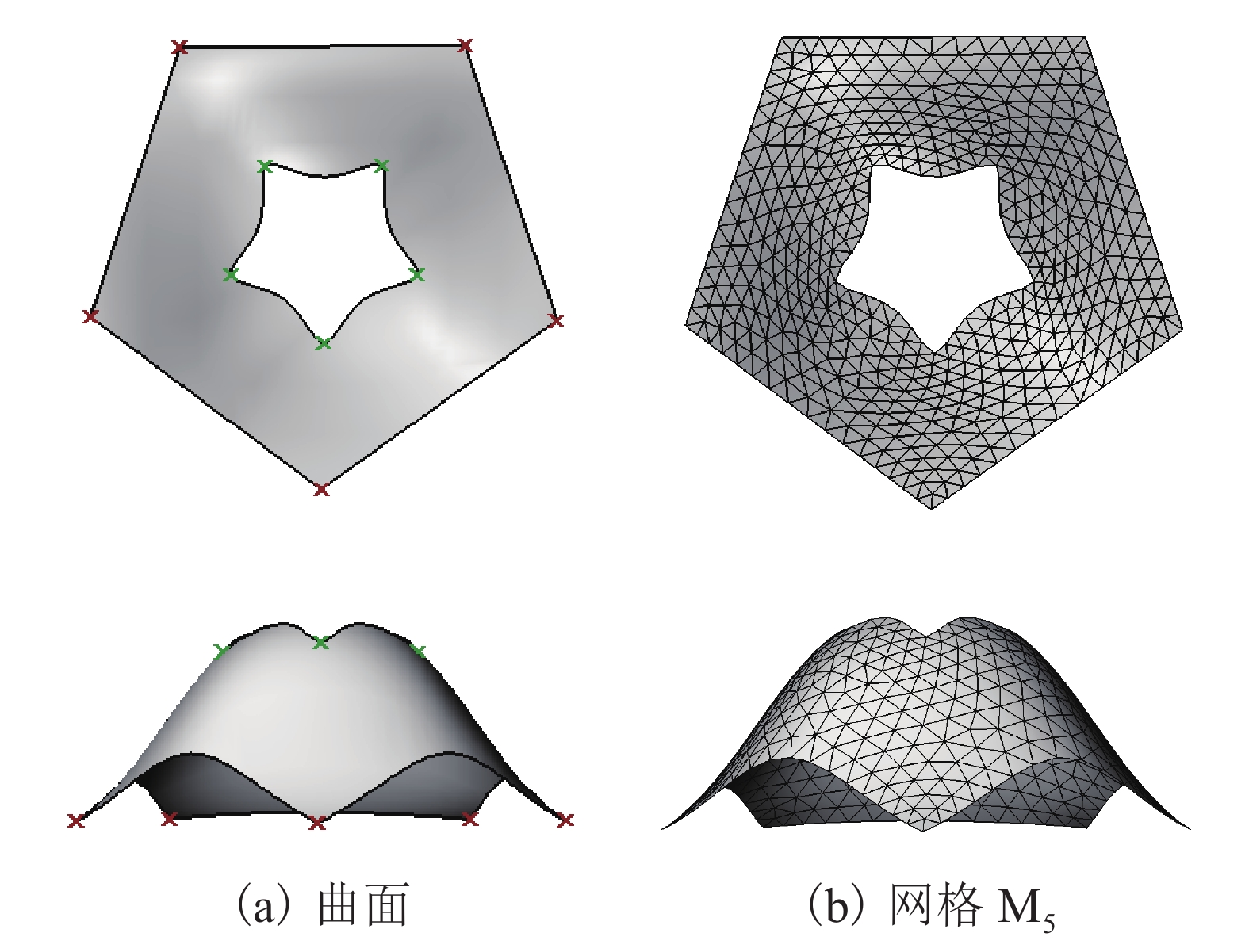
摘要: 为了在自由曲面上生成形状规整、大小可控的三角形网格,提出一种基于气泡运动模型的网格自动生成方法. 将适量的网格点布置在离散化的曲面上,并模拟为弹性气泡. 引入气泡间的相互作用力和曲面对气泡的吸附力,得到各气泡的运动控制方程. 采用数值方法近似求解气泡系统的平衡状态. 将平衡后的气泡中心用曲面Delaunay法连接成曲面上的三角形网格. 在气泡模型中,通过相对半径函数控制各气泡的相对大小,进而实现对网格大小的调控. 通过在相对半径函数中考虑气泡中心到特定点或线的距离、参考线或曲面的曲率等因素的影响,生成网格大小与曲面特征相适应的三角形网格. 6个算例结果表明,该方法生成的网格形状规整、疏密有致,其形状质量指标都高于0.97;该方法为网格结构的设计提供了参考.Abstract: To generate triangular grids with regular shapes and adaptive sizes over free-form surfaces, an automatic grid generation method is presented on the basis of a bubble dynamic model. Grid nodes were first decorated on the discretized surface according to certain rule, and were regarded as elastic bubbles. The inter-bubble forces and the forces from surface adsorption were introduced. The motion control equations of bubbles were established. Then, the equilibrium state of the bubble system was acquired by the numerical simulation algorithm. Finally, the centers of balanced bubbles were connected into a triangular grid by an extended Delaunay method. In the bubble model, the size of a bubble is determined by the relative radius function. And the control of the grid size is realized by adjusting the bubble size. Through the relative radius function factoring in the distance from each bubble center to selected points or curves, the curvature of reference curves or the surface and so on, the method can generate triangular grids with edges adapted to the surface features. Six cases have demonstrated that the grids generated by the proposed method have regular shapes and adaptive sizes, with their shape quality indexes all higher than 0.97. The method provides the convenience for the design of grid structures.
-
Key words:
- free-form surface /
- grid structure /
- grid generation /
- bubble-like method /
- grid control
-
表 1 网格质量评价
Table 1. Quality evaluation of grids
对象 调控方式 杆长 形状质量指标 平均值/m 离散系数 平均值 方差/× 10−4 M1 均匀 5.11 0.063 0.988 2.92 M2 距离 2.49 0.184 0.978 6.32 M3 距离 3.39 0.149 0.976 7.68 M4 曲率 2.56 0.141 0.977 6.82 M5 综合 3.89 0.151 0.977 6.62 M6 均匀 5.25 0.162 0.935 28.6 -
崔昌禹,崔国勇,涂桂刚,等. 基于B样条的自由曲面结构形态创构方法研究[J]. 建筑结构学报,2017,38(3): 164-172.CUI Changyu, CUI Guoyong, TU Guigang, et al. Structure morphogenesis of free-form surfaces based on B-spline[J]. Journal of Building Structures, 2017, 38(3): 164-172. 董磊. 单层自由曲面空间网格结构新型节点开发及风工况下结构稳定承载力分析[D]. 南京: 东南大学, 2015. 石伟志. 自由曲面结构力学性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2010. 李承铭,卢旦. 自由曲面单层网格的智能布局设计研究[J]. 土木工程学报,2011(3): 1-7.LI Chengming, LU Dan. Study of intelligent layout design of single-layer lattice shell of free form surface[J]. China Civil Engineering Journal, 2011(3): 1-7. SU L, ZHU S, XIAO N, et al. An automatic grid generation approach over free-form surface for architectural design[J]. Journal of Central South University, 2014, 21(6): 2444-2453. doi: 10.1007/s11771-014-2198-7 危大结,舒赣平. 自由曲面网格的划分与优化方法[J]. 建筑结构,2013,43(19): 48-53.WEI Dajie, SHU Ganping. Mesh generation and optimization method for free-form surface grid[J]. Building Structure, 2013, 43(19): 48-53. 潘炜,吴慧,李铁瑞,等. 基于曲面展开的自由曲面网格划分[J]. 浙江大学学报(工学版),2016,50(10): 1973-1979.PAN Wei, WU Hui, LI Tierui, et al. Grid generation on free-form surface based on surface flattening[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(10): 1973-1979. PERSSON P O, STRANG G. A simple mesh generator in MATLAB[J]. Siam Review, 2004, 46(2): 2004. SHIMADA K, GOSSARD D C. Bubble mesh: automated tri-angular meshing of non-manifold geometry by sphere packing[C]//Proceedings of the Third ACM Symposium on Solid Modeling and Application. New York: ACM Press, 1995: 409-419 SHIMADA K, GOSSARD D C. Automatic triangular mesh generation of trimmed parametric surfaces for finite element analysis[J]. Computer Aided Geometric Design, 1998, 15(3): 199-222. doi: 10.1016/S0167-8396(97)00037-X ZHELEZNYAKOVA A L. Molecular dynamics-based triangulation algorithm of free-form parametric surfaces for computer-aided engineering[J]. Computer Physics Communications, 2015, 190: 1-14. doi: 10.1016/j.cpc.2014.12.018 ZHELEZNYAKOVA A L, SURZHIKOV S T. Molecular dynamics-based unstructured grid generation method for aerodynamic applications[J]. Computer Physics Communications, 2013, 184(12): 2711-2727. doi: 10.1016/j.cpc.2013.07.013 OWEN S. A survey of unstructured mesh generation technology[C]//7th International Meshing Roundtable. Berlin: Springer-Verlag, 1998: 239-267. 王奇胜,高博青,李铁瑞,等. 基于气泡吸附的自由曲面三角形网格生成方法[J]. 华中科技大学学报(自然科学版),2018,46(3): 98-102.WANG Qisheng, GAO Boqing, LI Tierui, et al. Automatic grid generation on free-form surface based on bubble-like adsorption[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2018, 46(3): 98-102. GROOT R D, WARREN P B. Dissipative particle dynamics:Bridging the gap between atomistic and mesoscopic simulation[J]. The Journal of Chemical Physics, 1997, 107(11): 4423-4435. doi: 10.1063/1.474784 ZHANG H, SMIRNOV A V. Node placement for triangular mesh generation by Monte Carlo simulation[J]. International Journal for numerical methods in engineering, 2005, 64(7): 973-989. doi: 10.1002/nme.1402 DAVID A. Qualitative measures for initial meshes[J]. International Journal for Numerical Methods in Engineering, 2000, 47(47): 887-906. -





 下载:
下载: