Present Situation and Prospect of Evacuated Tube Transportation System
-
摘要: 作为一种新型交通系统，真空管道运输系统将悬浮列车技术和低气压管道技术相结合，理论上能够最大限度地减小列车高速运行时的摩擦阻力和气动阻力.为了促进真空管道运输系统的发展，从基本原理角度，系统论述了真空管道运输系统的可行性及车辆、管道、驱动装置等子系统关键构成，指出了其快速、便捷、安全、环保和高效等优势；介绍了国内外真空管道运输系统的研究现状，包括美国ET3、美国Hyperloop、瑞士超高速地铁Swissmetro，以及西南交通大学真空管道高温超导磁悬浮车试验平台，比较分析了各单位在车辆、管道、驱动装置及造价等方面的技术特点和优势；展望了当前发展真空管道运输系统亟需解决的关键问题，并指出车轨作用、高速直线牵引、气动和散热、管道密封以及管道内通信、救援这几个方面是今后需要重点研究的领域.Abstract: As a new type of transit system, the evacuated tube transportation system, combining magnetic levitation train technology and low-air-pressure tube technology, theoretically decreases friction and aerodynamic drag of high-speed trains as much as possible. In order to promote the evacuated tube transportation development, from the point of view of fundamental principles, the feasibility and the key components of vehicle, tube and propulsion were systematically discussed. Meanwhile, its advantages such as fast, convenience, safety, environmental protection and high efficiency were pointed out. The research status of the evacuated tube transportation system was introduced, including the ET3 (America), the Hyperloop (America), the Swiss Super High-speed Metro Swissmetro, and the evacuated tube high temperature superconducting maglev vehicle test platform of Southwest Jiaotong University. Their technical characteristics and advantages in vehicle, tube, propulsion device and cost were compared and analyzed. The key development and research issues which need to be urgently solved were prospected, such as train/track interaction, high-speed linear propulsion, aerodynamics and heat dissipation, tube sealing, in-pipe communication and rescue.
-
超高性能混凝土（UHPC）近年来得到了广泛的关注和研究，具有高强、高韧、高耐久性等诸多优点[1-3]. UHPC通常需要高温养护来获得超高性能，从工程应用角度来看，预制装配式结构更适合其发挥特长. UHPC节段装配式桥梁目前已经在工程中得到应用，这种桥梁在纵桥向进行分段，由预应力钢束将各节段连成整体. 由于普通钢筋在接缝处断开，且混凝土不连续，因此，接缝是潜在的抗剪薄弱环节. 键齿接缝是节段装配式桥梁最为广泛采用的连接形式之一，UHPC键齿接缝的抗剪承载力及其设计也因此成为行业关注的重点.
目前，国内外对普通混凝土键齿接缝抗剪性能的研究已较为深入. 在已有抗剪承载力计算方法中，认可度较高的大致有2种：一种是采用数理统计方法进行回归拟合；另一种是基于莫尔应力圆结合破坏准则进行理论推导. 前者如Buyukozturk等[4-5]的研究成果，由大量试验数据拟合得到的计算方法虽然预测精度较好，但理论性稍有欠缺，无法直接反映键齿接缝的受剪机理；后者则以美国德州大学的Roberts等[6]所建立的45° 斜压杆模型为典型代表，该方法已有很多衍生模型，由于力学机制相对明确，得到了众多学者的继承沿用[7-11]. 针对UHPC键齿接缝，刘桐旭[9]通过直剪试验发现，提高侧压力和UHPC抗拉强度或加入钢纤维均可提高键齿干接缝的抗剪承载力. Jiang等[10]通过10个推出试件研究了活性粉末混凝土（RPC）键齿干接缝的抗剪性能及其影响因素，基于莫尔应力圆，提出了RPC键齿干接缝抗剪承载力的简化计算公式. 王景全等[11-12]基于试验和数值模拟，各自提出了UHPC干接缝大键齿的合理深齿比和倾角. 上述研究主要针对干接缝，在胶接缝方面，闫泽宇[13]开展了3组UHPC键齿试件的剪切试验，通过回归分析给出了接缝抗剪承载力的拟合公式. 郑凡等[14]基于11个UHPC键齿胶接缝试件的直剪试验结果，考虑胶层黏结、接缝面摩擦和键齿等的贡献，建立了接缝抗剪承载力计算公式. 然而，由于接缝类型不同，加上UHPC材性差异较大，目前关于UHPC键齿接缝抗剪承载力计算公式引入的参数较多，往往存在特定的适用范围，公式形式较复杂且不统一，距离工程应用还有较大差距.
本文依托某拟建的节段装配式UHPC箱梁桥，针对其键齿接缝的抗剪承载力展开试验和理论研究. 将UHPC材料强度作为影响因素，基于剪压强度准则，推导得到了键齿接缝抗剪承载力计算公式，研究成果可为UHPC键齿接缝抗剪分析与设计提供参考.
1. 试验概况
1.1 试件设计及材料性能
某拟建主跨40 m的UHPC节段装配式简支箱梁桥分幅设置，每幅箱宽5.5 m，纵向分为3个节段（12.975 + 14 + 12.975）m，设有2个完全相同的胶接缝，选取其中一个作为试验原型. 根据其结构设计参数，采用足尺模型设计了1个UHPC平接缝试件和5个UHPC单键齿接缝试件，前者用于研究接触面摩阻力，后者包括干接缝和胶接缝2种类型以及4种侧压应力. 在参考已有试验研究的基础上，考虑依托工程的实际侧压力变化范围，选用3、6、9、12 MPa来模拟体外钢束所施加的力，为便于描述，按“侧压应力-接缝类型”来命名试件，如在F3-P、F3-G和F3-J中，F3代表侧压应力为3 MPa；P代表平接缝，G代表干接缝，J代表胶接缝. 试件参数如表1所示.
表 1 试件参数Table 1. Specimen parameters试件
编号接缝
类型设计侧压
应力/MPa实际侧压
应力/MPa预估承
载力/kNF3-P 平接缝 3 3.13 86.40 F3-G 干接缝 3 3.05 263.17 F3-J 胶接缝 3 2.99 526.40 F6-J 胶接缝 6 6.05 589.53 F9-J 胶接缝 9 9.01 646.66 F12-J 胶接缝 12 12.04 698.57 为防止试验过程中侧压力偏转，键齿接缝试件采用三段式设计，如图1（a）所示. 其中，中段为双向凸齿构造，左、右段均为凹齿构造；中段及左、右段的试验部分厚度均为120 mm；左、右段外侧局部加厚至280 mm，以使键齿结构侧向受力均匀. 试件的齿根宽度为100 mm，齿尖宽度为50 mm，齿深为40 mm；键齿上、下平接面宽度分别为50 mm，胶层厚度为2 mm. 平接缝试件的轮廓尺寸与键齿接缝试件一致，如图1（b）所示.
UHPC材料与依托工程完全一致，采用平直钢纤维，纤维直径为0.2 mm，长13 mm，抗拉强度大于
2000 MPa，体积掺量为2%. 与试件同时浇筑100 mm × 100 mm × 100 mm立方体和100 mm × 100 mm × 300 mm棱柱体各12个，按照标准试验方法[15]测得抗压强度fcu=160.0 MPa，轴心抗压强度fc=147.6 MPa，静力受压弹性模量Ec=47.4 GPa，泊松比γ=0.23. 环氧胶采用湖南固特邦公司生产的JN-P结构拼接缝胶，由A、B 2组胶体组成，两者按质量1∶3进行配比.1.2 加载及测量方案
如图2所示，采用两块厚30 mm的侧压板和4根直径36 mm的高强螺杆为试件施加侧压力，在螺母和承压钢板之间设置压力传感器以测量螺杆的拉力，设计和实际初始侧压应力如表1所示. 采用10 MN伺服压力机进行加载，将试件置于压力机承台上，底部用细砂垫平，顶部放置钢垫板，钢垫板上放置力传感器，试验加载前用水平尺对试件进行调平. 在试件中段底部和左右段对应处布置位移计，以测量接缝面的相对滑移. 将试件表面涂白，并绘制5 cm × 5 cm的网格线，以便观察裂缝发展情况.
采用力加载控制方式，分预加载和正式加载2个阶段，两阶段采用相同的荷载级，并分别记录应变、滑移等相关数据. 试验前采用Vf =μσnAsm对平接缝试件的抗剪承载力进行预估. 其中：Asm为平接面面积；σn为接缝所受的侧压应力；μ为胶接缝的摩擦系数，参考Gopal等[7]的建议近似取0.6. 同时，采用式（1）对键齿接缝试件的抗剪承载力进行预估[7].
V={(−0.009σn+0.59)Asm+Aj√(ft+σn2)2−(σn2)2,干接缝,C(Asm+Ake)+(−0.007σn+0.54)Asm+Aj√(ft+σn2)2−(σn2)2,胶接缝, (1) 式中：Aj为接缝面面积；$ {f_{\text{t}}} $为UHPC的极限抗拉强度，高温养护UHPC的拉压关系可取$ 0.648\sqrt {f_{\text{ck}}} $，$ {f_{\text{ck}}} $为UHPC圆柱体抗压强度，近似取轴心抗压强度$ {f_{\text{c}}} $；C为胶层与UHPC间的黏结力，文献[7]建议C=3.7 MPa；Ake为胶层面积.
采用式（1）对6个试件的抗剪承载力进行预估，如表1所示. 试验时，首先进行预加载以消除装置间的缝隙，荷载大小取试件预估承载力的20%；在正式加载中，试件开裂前的荷载级采用其预估承载力的1/20，加载速度为20～25 kN/min；开裂后的荷载级降为15～20 kN，加载速度降为10 kN/min，以便观察裂缝发展情况. 每级加载后待应变片及位移计读数稳定后再读取相关数据.
2. 试验结果与分析
2.1 试验现象
5个键齿接缝试件的加载现象类似，在加载初期无明显现象，当接近极限荷载的60%时，试件中段的键齿根部下方出现斜向上的裂缝，与水平方向的夹角约为60°，该裂缝在后续加载中发展较缓；继续加载后，键齿根部出现竖向裂缝，其附近还有多条平行裂缝；当竖向裂缝发展到一定程度后，试件由于钢纤维被拔出而发出“滋滋”声，此时竖向裂缝开始剧烈发展，多条平行小裂缝在剪力作用下逐渐连接成主裂缝，并向上贯穿；当接近极限荷载时，主裂缝从表面贯穿了键齿根部，键齿上、下平接面附近的UHPC产生了明显的错动；当达到极限荷载时，试件中段两侧键齿的根部在短时间内先后剪断，并发出巨大的声响. 试件具有明显的脆性破坏特点，如图3所示.
平接缝试件在加载初期也没有明显现象，当加载至98.92 kN时试件发出“滋滋”声，右侧接缝的胶体出现裂隙，而左侧接缝的胶体仍几乎完好. 继续加载时，接缝处开始出现滑移，但由于加载对中或试件制作等问题，左右两侧接缝处的滑移存在不对称现象. 当加载至207.53 kN时，右侧接缝的胶体与UHPC脱离，部分胶体发生断裂，加载终止，如图4所示.
2.2 试验结果
图5为各试件的荷载-滑移曲线，除了F3-J以外，其余试件的初始刚度都比较接近. 从曲线初始段的发展趋势来看，在对F3-J进行加载时试验装置之间可能仍存在未完全闭合的间隙，导致其初始刚度较小. 此外，由于存在不对称现象，平接缝试件F3-P是以右侧接缝的滑移位移为依据绘制的，脆性破坏特征不是很明显，其开裂和极限荷载均明显低于键齿接缝试件. 5个键齿接缝试件的曲线发展趋势较为接近，当键齿根部出现竖向裂缝后，试件刚度逐渐下降，竖向裂缝逐渐发展为主裂缝；当荷载接近峰值时，主裂缝贯穿整个键齿根部；进入破坏阶段后，个别试件的荷载-滑移曲线存在短暂的平台段，如F3-J；当键齿根部被剪断后，试件滑移陡增，荷载急降，表现出较明显的脆性破坏特征. 对比F3-G和F3-J可以看到，相同侧压应力下胶接缝的抗剪承载力（756.29 kN）比干接缝（623.70 kN）大21.3%，由于接缝面胶体承担的剪力比干接缝摩擦力更大，而且胶接缝试件的整体性比干接缝更好，可更好地发挥UHPC的高强材性.
图6为不同侧压应力下4个键齿胶接缝试件的荷载对比.
由图可见：开裂荷载和极限荷载均随侧压应力的增大而增大. 当侧压应力为6、9、12 MPa时，开裂荷载分别为542.29、678.47、757.00 kN，比3 MPa时分别增大了20.2%、50.4%和67.8%；极限荷载分别为836.75、927.55、960.11 kN，比3 MPa时分别增大了10.6%、22.6%和26.9%；试件的开裂荷载与极限荷载之比与侧压应力近似成线性关系.
3. 基于剪压强度准则的计算方法
由表1和图5可知，式（1）的预估承载力明显偏低，有必要对UHPC键齿接缝的抗剪承载力作进一步的研究. 一般认为，键齿接缝的抗剪承载力主要由接缝面的摩擦力（Vf）和键齿的抗剪力（Vk）组成，且后者占主导作用. 将键齿接缝视为一个倾斜角为α的斜压杆，如图7（a）所示，图中：h为键齿接缝的高度，w为比拟斜压杆的宽度. 采用摩尔应力圆理论求解键齿根部的目标剪应力τ[6-10]，最后求得Vk（Vk=τAk，Ak为键齿根部面积）.
本文沿用上述假设，但采用八面体应力公式和剪压强度准则来推导τ. 以单键齿接缝为例进行说明（多键齿接缝类似），如图7（b）、（c）所示（σx为水平正应力，σy为竖向正应力），键齿根部的一个微元体处于双向受压应力和剪应力的复合应力状态. 蒋大骅[16-17]通过对比研究发现，复合应力状态与图7（d）所示的单向剪压应力状态在破坏模式上较为接近，均近似满足剪压强度准则，如式（2）.
τoctfc=aσoctfc+b, (2) 式中：a、b为系数，可分别取a=−1.15，b=0.087[16]；τoct和σoct分别为八面体应力，如式（3）、（4）.
σoct=13(σ1+σ2+σ2), (3) τoct=13√(σ1−σ2)2+(σ2−σ3)2+(σ3−σ1)2, (4) 式中：σ1、σ2、σ3分别为第一、第二、第三主应力，在如图7（c）平面应力状态下σ2=0，σ1、σ3如式（5）、（6）.
σ1=12(σx+σy)+12√(σx−σy)2+4τ2xy, (5) σ3=12(σx+σy)−12√(σx−σy)2+4τ2xy, (6) 式中：τxy即为键齿根部的剪应力.
将式（5）、（6）代入式（3）、（4）可得
σoct=13(σx+σy), (7) τoct=13√2(σ2x+σ2y−σxσy+3τ2xy). (8) 由图7（a）可知：水平正应力σx=−σn；Roberts等[6]基于试验结果根据比拟斜压杆模型建议σy=−τ，这一结论后来被大量学者引用[9-10,18]，也被美国AASHTO（美国国家公路与运输协会）规范[19]所采纳，本文因此沿用这一结论.
将式（7）、（8）代入式（2），考虑到σx=−σn和σy=−τ，可得
−a(σn+τ)+3bfc=√(σn−τ)2+σ2n+7τ2. (9) 求解式（9）并舍去较小解可得
τ=[σn(a2+1)−3abfc+√4a2σ2n−18abfcσn+24b2f2c−5σ2n]8−a2. (10) 将a=−1.15，b=0.087[16]代入式（10）可得
τ=0.045fc+0.348σn+0.11√(fc+4.955σn)2−22.956σ2n. (11) 统计[4,7-10,13-14,18]发现，键齿接缝的侧压应力σn大都低于$ 0.1{f_{\text{c}}} $，因此，式（11）中22.956$ \sigma _{\text{n}}^2 $仅约为$ {\left( {{f_{\text{c}}} + 4.955{\sigma _{\text{n}}}} \right)^2} $的10%. 若将22.956$ \sigma _{\text{n}}^2 $舍去，式（11）就可转变为
τ=0.155fc+0.9σn. (12) 由此得到UHPC键齿接缝抗剪承载力为
Va=Vk+Vf=(0.155fc+0.9σn)Ak+μσnAsm. (13) 对于干接缝试件的摩擦系数，美国混凝土协会[20]（ACI）建议，当约束应力比（即$ \sigma_{{\mathrm{n}}} / f_{{\mathrm{c}}} $）小于0.1时，摩擦系数为0.60；刘桐旭[9]根据试验结果，以约束应力比为参数给出了μ的拟合公式，其值也集中在0.60附近；Gopal等[7]也提出了类似的经验公式，取值也以0.60为基准，因此本文沿用0.60. 胶接缝试件的摩擦系数μ在取值上仍有争议，Gopal等[7]建议的取值与干接缝接近，但由表1可知，其理论计算值仅为F3-P实测值的41.63%，明显偏小. 根据F3-P试件的实测结果来反算，可得摩擦系数μ约为1.38. 该数值与美国AASHTO规范[19]针对整体浇筑混凝土所建议的摩擦系数1.40非常接近. 鉴于4个胶接缝试件在破坏时表现出良好的整体性，本文采用1.40作为其平接面摩擦系数，但该数值仍有待进一步验证. 式（13）对多键齿接缝也是适用的，只是Ak和Asm要相应地变化.
4. 计算方法评价
4.1 本文试验结果分析
为便于表述，定义比值系数λ=Vc/Vt，其中Vc、Vt分别为计算值和实测值，λ越接近1说明计算值越接近实测值，λ>1说明计算值高估了承载力，λ<1说明计算值较为保守. 同时定义$ \overline \lambda $、λcov和Sλ分别为比值系数的均值、变异系数和平均绝对误差，$ \overline \lambda $可反映计算方法总体上是否保守，$ \overline \lambda $>1表示计算方法总体偏大，$ \overline \lambda $<1表示计算方法总体偏保守；λcov越小表示计算方法的离散程度越低；$ {S_{\text{λ}} } $反映计算方法的精度，Sλ越小表示计算方法精度越高.
由表2和图8可见，采用式（13） 计算后，5个键齿试件的计算误差分别为5%、−6%、5%、13%和26%，平均绝对误差为11%，表明式（13）可较为准确地预测本文5个UHPC键齿接缝的抗剪承载力，但计算值整体偏大. 5个试件比值系数的变异系数λcov=0.10，表明式（13）的计算离散性较低，计算效果较理想.
表 2 试件抗剪承载力对比Table 2. Comparison of shear bearing capacity of specimens试件编号 Vt/kN Vc/kN λ $ \overline \lambda $ Sλ λcov F3-G 623.7 657.1 1.05 1.09 0.11 0.10 F3-J 756.3 714.7 0.94 F6-J 836.8 880.3 1.05 F9-J 927.6 1045.9 1.13 F12-J 960.1 1211.5 1.26 4.2 已有试验结果分析
由于本文试件数量有限，本节结合已有试验数据对式（13）作进一步对比分析. 从文献[7,9-10,13-14,18]中统计了62个UHPC键齿接缝的剪切试验结果，接缝形式有干接缝和胶接缝，侧压应力的范围为1～24 MPa，约束应力比的范围为0.82%～22.57%，键齿数量有单键齿和多键齿. 试件破坏形式均与本文试验类似的键齿剪断破坏.
图9为采用式（13）计算得到的理论值与实测值的对比：62个试件中有7个试件的计算误差在−30%以外，占比11.3%；有22个试件的计算误差为−30%～−10%，占比35.5%；有16个试件的计算误差在−10%～10%，占比25.8%；有9个试件的计算误差为10%～30%，占比14.5%；有8个试件的计算误差在30%以外，占比12.9%. 62个试件的比值系数均值$ \overline{\lambda} $=0.99，其中58%的计算值低于实测值，表明式（13）总体稍偏保守；有超过75%的计算绝对误差低于30%，平均绝对误差Sλ=0.21，表明式（13）总体精度较高. 比值系数的变异系数λcov=0.26，但超过60%的数据点集中分布在−30%～10%误差线内，表明式（13）的计算结果有一定离散性，但总体较为稳定.
4.3 影响参数分析
将62个试件根据键齿数量、接缝形式、约束应力比等影响参数进行分类，分析结果如表3.
表 3 参数分析结果Table 3. Analysis results of influencing parameters影响参数 试件数量/个 $ \overline \lambda $ Sλ λcov 键齿数量 单键齿 35 0.92 0.20 0.25 多键齿 27 1.08 0.21 0.25 接缝形式 干接缝 38 0.96 0.18 0.22 胶接缝 24 1.03 0.25 0.31 约束应力比 ≤1% 9 0.93 0.15 0.16 （1%，2%] 13 0.89 0.24 0.27 （2%，5%] 16 0.87 0.17 0.20 （5%，10%] 15 1.09 0.19 0.21 >10% 10 1.22 0.29 0.25 1） 35个单键齿试件的$ \overline{\lambda} $=0.92，27个多键齿试件的$ \overline{\lambda} $=1.08，说明式（13）对单键齿试件抗剪承载力的预测偏低，但高估了多键齿试件的抗剪承载力，可能是推导过程未充分考虑多键齿间的耦合作用对抗剪承载力的削弱. 单键齿和多键齿试件的λcov均约为0.25，Sλ分别为0.20和0.21，表明式（13）对不同键齿数量的试件具有相似的计算精度和离散程度.
2） 38个干接缝试件的$ \overline \lambda $=0.96，24个胶接缝试件的$ \overline \lambda $=1.03，说明式（13）对胶接缝试件抗剪承载力的预测稍偏大，对干接缝试件的预测则偏保守，可能是高估了胶接缝试件的摩擦系数. 干接缝试件的Sλ=0.18，明显优于胶接缝试件的0.25，变异系数也明显更小，表明式（13）计算干接缝的效果在精度和离散程度方面均优于胶接缝.
3） 当约束应力比小于5%时，式（13）偏保守，且误差和离散程度都不大；当$ {{{\sigma _{\text{n}}}} \mathord{\left/ {\vphantom {{{\sigma _{\text{n}}}} {{f_{\text{c}}}}}} \right. } {{f_{\text{c}}}}} $处于5%～10%时，计算结果少量偏大，但误差和离散程度均较小；当$ {{{\sigma _{\text{n}}}} \mathord{\left/ {\vphantom {{{\sigma _{\text{n}}}} {{f_{\text{c}}}}}} \right. } {{f_{\text{c}}}}} $超过10%时，计算值偏大较多，且精度和离散程度均较差，其原因是推导过程舍去了相对较小项（−22.956$ \sigma _{\text{n}}^2 $），客观上放大了计算值. 当约束应力比较小时，舍去较小项对计算结果影响很小；当约束应力比较大时，该数值在结果中的占比有所提升，使计算结果偏大，且偏离程度会随着约束应力比的上升而变大.
5. 结 论
1） UHPC键齿接缝试件在破坏时主裂缝沿竖向贯穿整个键齿根部，具有明显的脆性破坏特征. 胶接缝比干接缝具有更好的整体性，更适合UHPC材性的发挥.
2） 在相同侧压应力下，胶接缝试件的极限荷载比干接缝大21.3%；当侧压应力由3 MPa分别增至6、9、12 MPa时，胶接缝试件的极限荷载分别增大10.6%、22.6%、26.9%.
3） 基于剪压强度准则，采用八面体应力公式推导得到的计算公式可较为准确地预测UHPC键齿接缝的抗剪承载力，5个键齿接缝试件的$ \overline \lambda $=1.09， Sλ=0.11，λcov=0.10，表明计算公式的精度较高、离散性较低.
4） 62个已有试件的计算结果表明，本文公式的总体比值系数均值为0.99，平均绝对误差为0.21，具有较好的预测精度和稳定性，且58%的计算值低于实测值，计算结果稍偏保守.
5） 本文公式对单键齿和干接缝试件抗剪承载力的预测偏低，对多键齿和胶接缝试件抗剪承载力的预测偏高. 约束应力比对本文公式的预测精度有一定的影响，当$ {{{\sigma _{\text{n}}}} \mathord{\left/ {\vphantom {{{\sigma _{\text{n}}}} {{f_{\text{c}}}}}} \right. } {{f_{\text{c}}}}} > 10{\text{%}} $时，计算效果相对较差.
致谢：感谢重庆交通大学研究生科研创新项目（2022S0004）对本研究工作的资助.
-
图 2 日本低温超导EDS列车
Figure 2. Low-temperature superconducting electrodynamic suspension train in Japan
图 3 中国高温超导磁悬浮列车“世纪号”
Figure 3. High temperature superconducting maglev vehicle“Century”in China
图 8 真空管道高温超导磁悬浮车实验平台Super-Maglev
Figure 8. Experimental facility named Super-Maglev for evacuated tube transport with high temperature superconducting maglev vehicle
表 1 几种悬浮技术的对比
Table 1. Comparison of several suspension technologies
项目 悬浮技术 常导磁悬浮 低温超导磁悬浮 高温超导磁悬浮 气动悬浮 路轨要求 高 较高 低 极高 控制系统 复杂 较复杂 简单 难以控制 悬浮状态 须耗能 低速需轮轨 静止悬浮 依靠气膜悬浮 悬浮高度/mm 8 100 10~30 0.5~1.3 成本 高 高 低 低 
下载: 导出CSV
表 2 各种运输系统能耗及成本对比
Table 2. Comparison of consumption and cost among several transport systems
指标 运输系统 水路 公路 铁路 民航 单位能耗/（×103 kg•t−1•km−1） 9 64 10 434 单位成本/（×103 元•t−1•km−1） 19 219 22 2 800
下载: 导出CSV
表 3 ET3、Swissmetro和Hyperloop系统参数对照
Table 3. Parameters comparison among ET3，Swissmetro and Hyperloop system
系统 车辆 管道 其它 规划 悬浮类型 形状 尺寸/m 车重/t 承载人数/位 结构 位置 材料 气压/kPa 驱动装置 供电装置 经费 试验线路及线路长度/km 最高时速/（km•h−1） ET3 磁悬浮 胶囊小车 直径1.30，长4.80 183×10−3 6 双向 10.13 直线电机 供电网和蓄电池 140万美元/km，2.8万美元/辆 纽约—好莱坞，
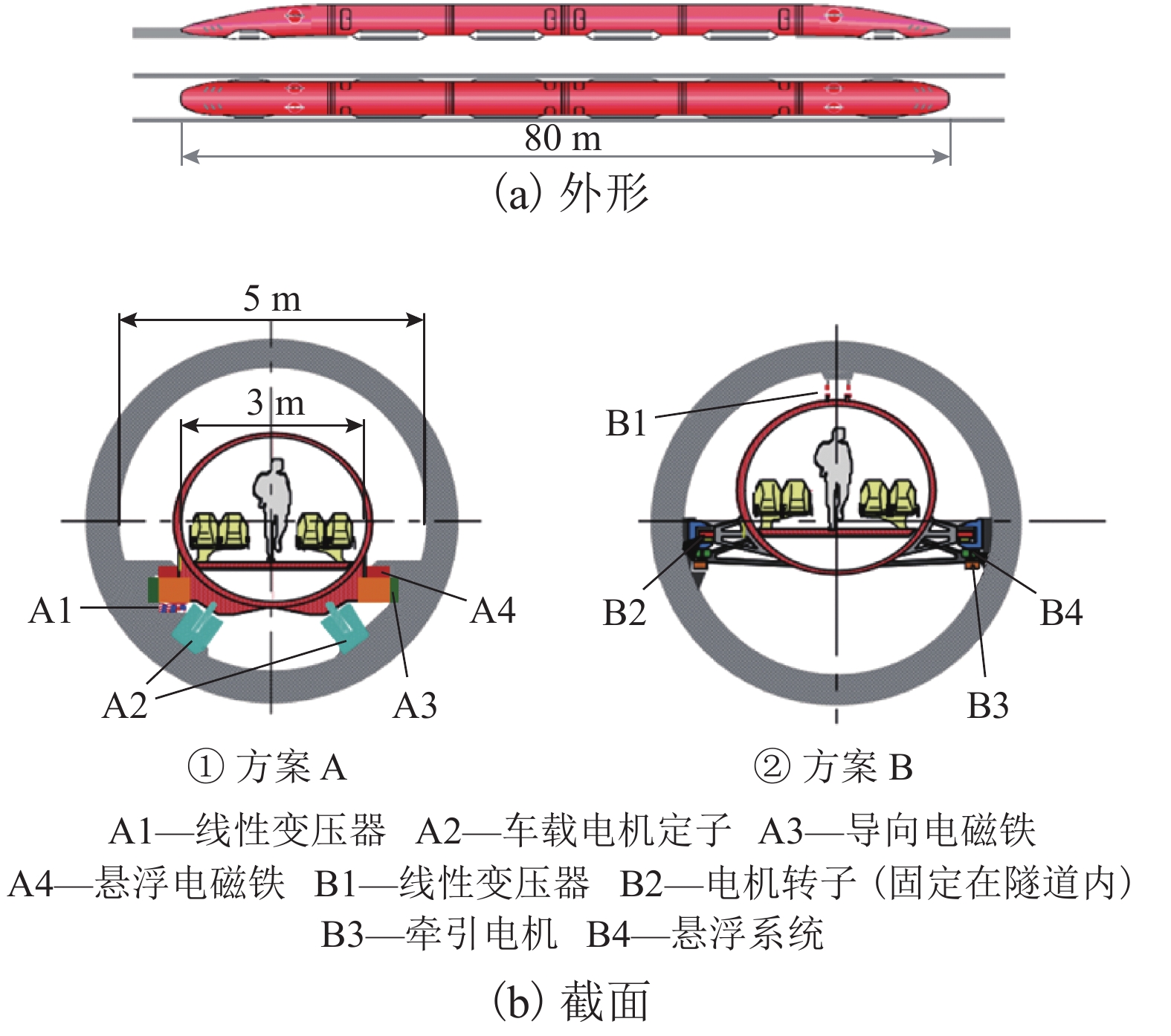
4 6006 500 Swissmetro 电磁悬浮 列车 直径3.50，长200.00 100 800 双向并行 地下隧道 钢筋混凝土管片 10.13 直线电机 供电网和蓄电池 50亿瑞士法郎 日内瓦—洛桑，63 500 Hyperloop 气动悬浮 Hyperloop 宽1.35，高1.10 15 28 双向并行 高架桥 金属 0.10 电动空气压缩机 太阳能和蓄电池 60亿美元 加州5号公路沿线，8 1 220
下载: 导出CSV
表 4 Super-Maglev具体参数
Table 4. Super-Maglev parameters
管道直径/m 长度/m 气压
/kPa实验速度/（km•h−1） 牵引制动 2.0 45.0，环形；弯道半径6.0，直线段长度3.6 101.0～
10.10～50 直线感应电机配合机械混合制动
下载: 导出CSV
-
GODDARD H R. Apparatus for vacuum tube transportation: U S, 2488287[P]. 1945-10-06. GODDARD H R. Vacuum tube transportation system: U S, 2511979[P]. 1950-06-20. KEMPER H. The invention of a hovertrack with wheelless vehicles which hover along iron rails using magnetic fields: Germany, DE1934K130005D[P]. 1934-08-11. 郝瀛. 中国铁路建设概论[M]. 北京: 中国铁道出版社, 1998: 294-295. MOSSI M, ROSSEL P. Swissmetro: a revolution in the high-speed passenger transport systems[C]//1st Swiss Transport Research Conference. Ascona: IEEE, 2001: 1-16. SOLTER M R. Trans-planetary subway systems: a burgeoning capability[R/OL]. Rand Organization, 1978 [2018-4-13]. https://www.rand.org/content/dam/rand/pubs/papers/2009/P6092.pdf. OSTER D, FLA R C. Evacuated tube transportation: U S, 5950543[P]. 1999-09-14. MUSK E. Hyperloop alpha[EB/OL]. 2013[2018-4-13]. http://www.spacex.com/sites/spacex/files/hyperloop_alpha.pdf. 沈志云. 关于我国发展真空管道高速交通的思考[J]. 西南交通大学学报,2005,40(2): 133-137. doi: 10.3969/j.issn.0258-2724.2005.02.001SHEN Zhiyun. On developing high-speed evacuated tube transportation in China[J]. Journal of Southwest Jiaotong University, 2005, 40(2): 133-137. doi: 10.3969/j.issn.0258-2724.2005.02.001 SCHETZ A J. 高速列车空气动力学[J]. 力学进展, 2003, 33(3): 404-423. 沈志云. 高速磁浮列车对轨道的动力作用及其与轮轨高速铁路的比较[J]. 交通运输工程学报,2001,1(1): 1-6. doi: 10.3321/j.issn:1671-1637.2001.01.001SHEN Zhiyun. Dynamic interaction of high speed maglev train on girders and its comparison with the case in ordinary high speed railways[J]. Journal of Traffic and Transportation Engineering, 2001, 1(1): 1-6. doi: 10.3321/j.issn:1671-1637.2001.01.001 吴祥明. 磁浮列车[M]. 上海: 上海科学技术出版社, 2003: 96-97. MOTOHARU O, SHUNSAKU K, HISAO O. Japan’s superconducting maglev train[J]. IEEE Instrumentation & Measurement Magazine, 2002, 5(1): 9-15. 王家素, 王素玉. 超导技术应用[M]. 成都: 成都科技大学出版社, 1995: 145-152. WANG Jiasu, WANG Suyu, ZENG Youwen, et al. The first man-loading high temperature superconducting maglev test vehicle in the world[J]. Physica C, 2002, 378/379/380/381: 809-814. SCHULTZ L, HAAS O, VERGES P, et al. Superconductively levitated transport system-the supratrans project[J]. IEEE Transactions on Applied Superconductivity, 2005, 15(2): 2301-2305. doi: 10.1109/TASC.2005.849636 SOTELO G G, OLIVEIRA R A H, COSTA F S, et al. A full scale superconducting magnetic levitation (maglev) vehicle operational line[J]. IEEE Transactions on Applied Superconductivity, 2015, 25(3): 1-5. KOVALEV K L, KONEEV S M A, POLTAVEC V N, et al. Magnetically levitated high-speed carriages on the basis of bulk HTS elements[C]//Proceeding of the 19th International Symposium on Magnetic Suspension Technology. Dresden: [s. n.], 2005: 51. D ’OVIDIO G, CRISI F, LANZARA G. A " V” shaped superconducting levitation module for lift and guidance of a magnetic transportation system[J]. Physica C, 2008, 468(14): 1036-1040. doi: 10.1016/j.physc.2008.05.154 杨学实. 气悬浮列车研究的新进展[J]. 交通运输系统工程与信息,2003,3(3): 66-70. doi: 10.3969/j.issn.1009-6744.2003.03.014YANG Xueshi. New developments in research of air suspension trains[J]. Communication and Transportation Systems Engineering and Information, 2003, 3(3): 66-70. doi: 10.3969/j.issn.1009-6744.2003.03.014 王家素,王素玉. 高温超导磁悬浮列车研究综述[J]. 电气工程学报,2015,10(11): 2-12.WANG Jiasu, WANG Suyu. High temperature superconducting maglev train[J]. Journal of Electrical Engineering, 2015, 10(11): 2-12. 张耀平,梅绍祖,曾学贵. ETT——引领21世纪的高速运输[J]. 世界科技研究与发展,2002,24(2): 60-64. doi: 10.3969/j.issn.1006-6055.2002.02.009ZHANG Yaoping, MEI Shaozu, ZENG Xuegui. ETT—lead the high-speed transportation of the 21st century[J]. World Sci-Tech R & D, 2002, 24(2): 60-64. doi: 10.3969/j.issn.1006-6055.2002.02.009 严作人. 运输经济学[M]. 北京: 人民交通出版社, 2009: 33-38. 董焰. 我国综合交通运输的效率、效益及管理体制问题[C]//中国工程院第32场工程科技论坛——中国综合交通运输发展战略. [出版地不详]: 中国工程院, 2004: 15-32. OSTER D, KUMADA M, ZHANG Y. Evacuated tube transport technologies (ET3) tm;a maximum value global transportation network for passengers and cargo[J]. Journal of Modern Transportation, 2011, 19(1): 42-50. doi: 10.1007/BF03325739 张瑞华等. 一种新的高速磁悬浮列车——瑞士真空管道高速磁悬浮列车方案[J]. 变流技术与电力牵引,2004(1): 44-46.ZHANG Ruihua, et al. A new high-speed maglev train-the swiss vacuum tube high-speed maglev train project[J]. High Power Converter Technology, 2004(1): 44-46. CASSAT A, ESPANET C. Swissmetro: combined propulsion with levitation and guidance[C]//Proceedings of Maglev. Shanghai: [s. n.], 2004: 747-758. 刘本林, 赵勇. 速车系统概论[M]. 成都: 西南交通大学出版社, 2009: 16-26. ZHOU Dajin, CUI Chenyu, ZHAO Lifeng, et al. Running stability of prototype vehicle in side-suspended HTS maglev circular test track system[J]. IEEE Transactions on Applied Superconductivity, 2017, 27(1): 3600107. DENG Zigang, ZHANG Weihua, ZHENG Jun, et al. A high temperature superconducting maglev ring test line developed in Chengdu,China[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(6): 3602408. DENG Zigang, ZHANG Weihua, ZHENG Jun, et al. A high-temperature superconducting maglev-evacuated tube transport (HTS Maglev-ETT) test system[J]. IEEE Transactions on Applied Superconductivity, 2017, 27(6): 3602008. 王博. 真空管道高温超导磁悬浮车气动特性研究[D]. 成都: 西南交通大学, 2017. 刘加利,张继业,张卫华. 真空管道高速列车气动特性分析[J]. 机械工程学报,2013,49(22): 137-143.LIU Jiali, ZHANG Jiye, ZHANG Weihua. Analysis of aerodynamic characteristics of high-speed trains in the evacuated tube[J]. Journal of Mechanical Engineering, 2013, 49(22): 137-143. 贾文广. 真空管道交通系统热动力学特性研究[D]. 青岛: 青岛科技大学, 2013. LIU Lu, WANG Jiasu, WANG Suyu, et al. Levitation force transition of high-Tc superconducting bulks within a maglev vehicle system under different dynamic operation[J]. IEEE Transactions on Applied Superconductivity, 2011, 21(3): 1547-1550. doi: 10.1109/TASC.2010.2091099 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 781
- HTML全文浏览量: 343
- PDF下载量: 95
- 被引次数: 0