基于比值更新的索穹顶结构找力分析方法

姜正荣; 刘小伟; 石开荣; 林全攀

doi:10.3969/j.issn.0258-2724.20180201

基于比值更新的索穹顶结构找力分析方法

doi: 10.3969/j.issn.0258-2724.20180201

姜正荣^1,2,,
刘小伟¹,
石开荣^1,2, ,,
林全攀¹

基金项目: 广州市科技计划项目（1563000257）；亚热带建筑科学国家重点实验室开放课题（2019ZB27）

详细信息

作者简介:
姜正荣（1971—），男，副教授，博士，研究方向为大跨度空间结构，E-mail：zhrjiang@scut.edu.cn

通讯作者:
石开荣（1978—），男，副教授，博士，研究方向为预应力钢结构，E-mail：krshi@scut.edu.cn

中图分类号: TU394
计量
- 文章访问数: 508
- HTML全文浏览量: 275
- PDF下载量: 13
- 被引次数: 0
出版历程
- 收稿日期: 2018-03-19
- 修回日期: 2018-08-12
- 网络出版日期: 2018-12-21
- 刊出日期: 2020-02-01

Method of Force-Finding Analysis Based on Ratio Updating for Cable Domes

摘要

摘要: 为了快速高效求解索穹顶结构的预应力分布，提出了一种基于比值更新的找力新方法. 以不断更新的索预应力比值来分配拉索预应力，以索力和位形作为收敛控制参数，迭代得到满足精度要求的预应力分布. 基于此，首先对索穹顶结构进行了不考虑重力影响的找力分析，验证了该方法的正确性；其次当考虑重力影响且每个索段划分为多个单元时，可引入沿索长的索水平分力这一不变量，将索力的比值替换为索水平分力的比值. 结果表明：基于比值更新的找力分析方法计算速度快，位形偏差小，精度高；考虑重力影响的找力分析结果与不考虑重力影响相差较大（最大为19.34%），索穹顶结构的找力分析宜考虑重力的影响；将每个索段划分为单个单元和多个单元的找力分析结果相差甚微（最大仅0.05%），当索预应力较大且索长较短时，可将每个索段划分为单个单元以简化求解预应力分布.
- 索穹顶结构 /
- 找力分析 /
- 基于比值更新的找力分析方法 /
- 索水平分力
Abstract: In order to determine the prestress distribution of cable domes efficiently, a new method of force-finding analysis based on ratio updating was proposed. In this method, values of cable prestresses are pre-assumed and then constantly adjusted according to the continuously updated ratio of cable prestress; the precise prestress distribution of cable dome is acquired by iterations using the cable force and geometric shape as convergence control parameters. In this way, a force-finding analysis of cable domes is first conducted without considering the gravity effect, which verifies the effectiveness of this method. When the gravity is considered, each cable segment is divided into multiple units. An invariant, the cable force’s horizontal component along the length is introduced and the ratio of cable force is then replaced by that of the horizontal component force to deal with the situation with gravity. The results show that the method of force-finding analysis based on ratio updating is characterized by fast computational speed, small geometric shape deviation, and high precision. The results of force-finding analysis considering the influence of gravity are significantly different from those without considering gravity, and the maximum deviation reaches 19.34%. Thus, the influence of gravity should be taken into account in force-finding analysis of cable domes. In addition, whether each cable segment is divided into one unit or multiple units, the results of force-finding analysis make little difference (0.05% maximum deviation). Therefore, in cases when the cable prestress is large and cable length is short, each cable segment could be divided into only one unit to simplify the solving process of prestress distribution.
- cable dome /
- force-finding analysis /
- method of force-finding analysis based on ratio updating /
- horizontal component force of cable

HTML全文

图 1 分析模型

Figure 1. Analytical model

下载: 全尺寸图片幻灯片

图 2 索杆预应力分布

Figure 2. Cable-strut prestress distribution

下载: 全尺寸图片幻灯片

图 3 索段s示意

Figure 3. Schematic diagram of cable segment s

下载: 全尺寸图片幻灯片

图 4 索杆预应力分布

Figure 4. Cable-strut prestress distribution

下载: 全尺寸图片幻灯片

表 1 截面参数

Table 1. Section parameter

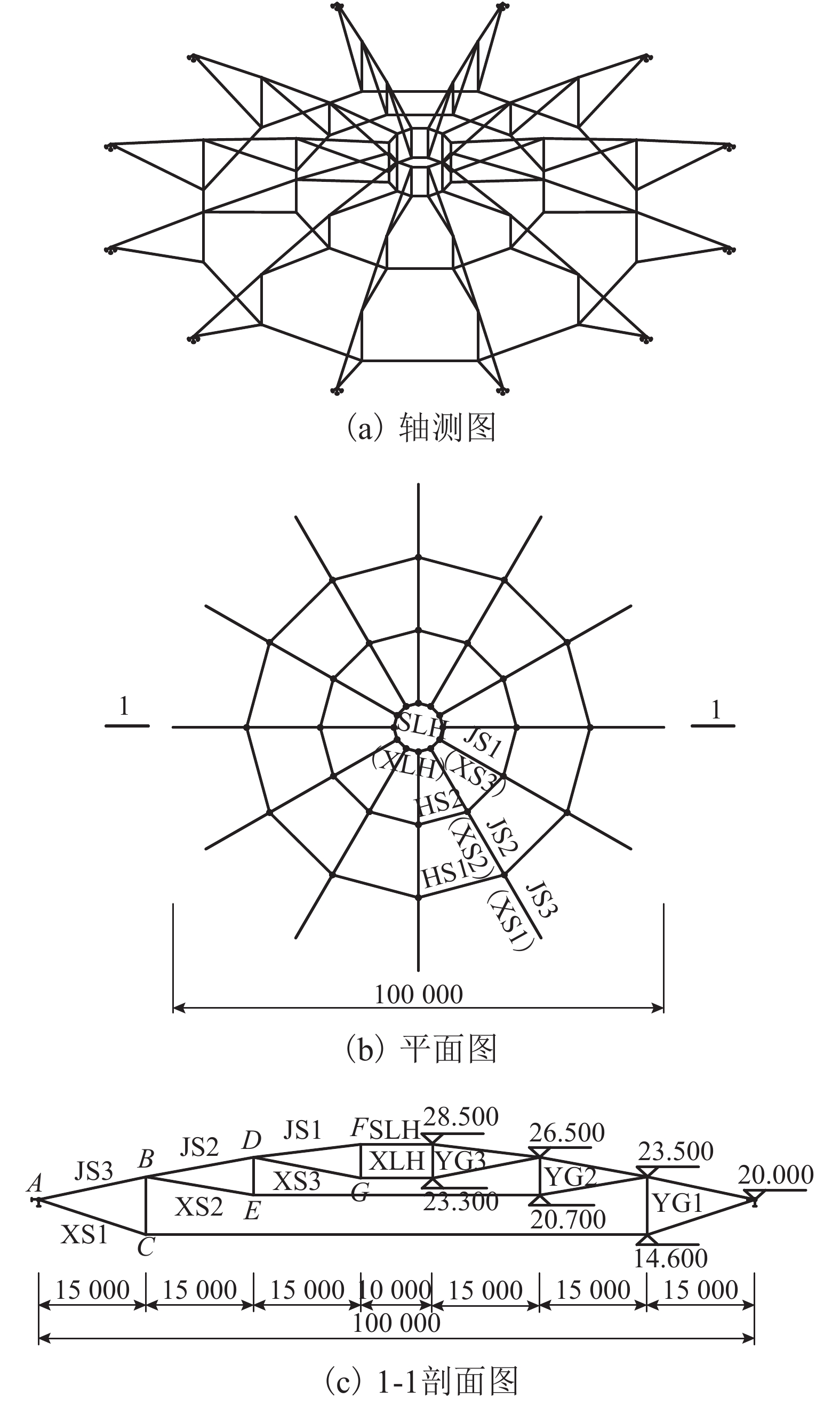
索杆编号	截面面积/mm²	索杆编号	截面面积/mm²
JS1	2 494.03	HS1	5 202.03
JS2	3 271.03	SLH	1 424.03
JS3	3 671.03	XLH	2 494.03
XS3	1 669.03	YG1	6 633.03
XS2	3 671.03	YG2	3 280.03
XS1	4 195.03	YG3	2 749.03
HS2	3 671.03

下载: 导出CSV

表 2 预应力分布对比

Table 2. Comparison of prestress distributions

索杆编号	预应力			预应力比值
索杆编号	文献[18]/kN	本文方法/kN	偏差/%	文献[18]	本文方法	偏差/%
JS1	435.33	435.33	0.00	1.000	1.000	0.00
JS2	715.33	715.09	−0.03	1.643	1.643	0.00
JS3	1 492.00	1 491.26	−0.05	3.427	3.426	−0.03
XS3	276.00	275.75	−0.09	0.634	0.633	−0.16
XS2	764.33	764.02	−0.04	1.756	1.755	−0.06
XS1	1 001.00	1 000.39	−0.06	2.299	2.298	−0.04
HS2	1 451.67	1 451.14	−0.04	3.335	3.333	−0.06
HS1	1 819.33	1 818.41	−0.05	4.179	4.177	−0.05
SLH	834.00	833.49	−0.06	1.916	1.915	−0.05
XLH	521.00	520.93	−0.01	1.197	1.197	0.00
YG1	−339.00	−338.83	−0.05	−0.779	−0.778	−0.13
YG2	−140.33	−140.23	−0.07	−0.322	−0.322	0.00
YG3	−57.67	−57.53	−0.24	−0.132	−0.132	0.00

下载: 导出CSV

表 3 找力后控制点竖向位置与设计初始态偏差值

Table 3. Deviation of the control point’s vertical position after force finding from that in the initial state of design

节点编号	控制点偏差/mm
B	0.045
C	0.045
D	0.097
E	0.097
F	0.030
G	0.030

下载: 导出CSV

表 4 找力后控制点竖向位置与设计初始态偏差值

Table 4. Deviation of the control point’s vertical position after force finding from that in the initial state of design mm

节点编号	划分为 1 个单元	划分为 3 个单元
B	0.028	0.047
C	0.028	0.047
D	0.104	0.085
E	0.104	0.085
F	0.031	0.025
G	0.031	0.025

下载: 导出CSV

表 5 找力分析结果对比

Table 5. Comparison of force-finding analysis results

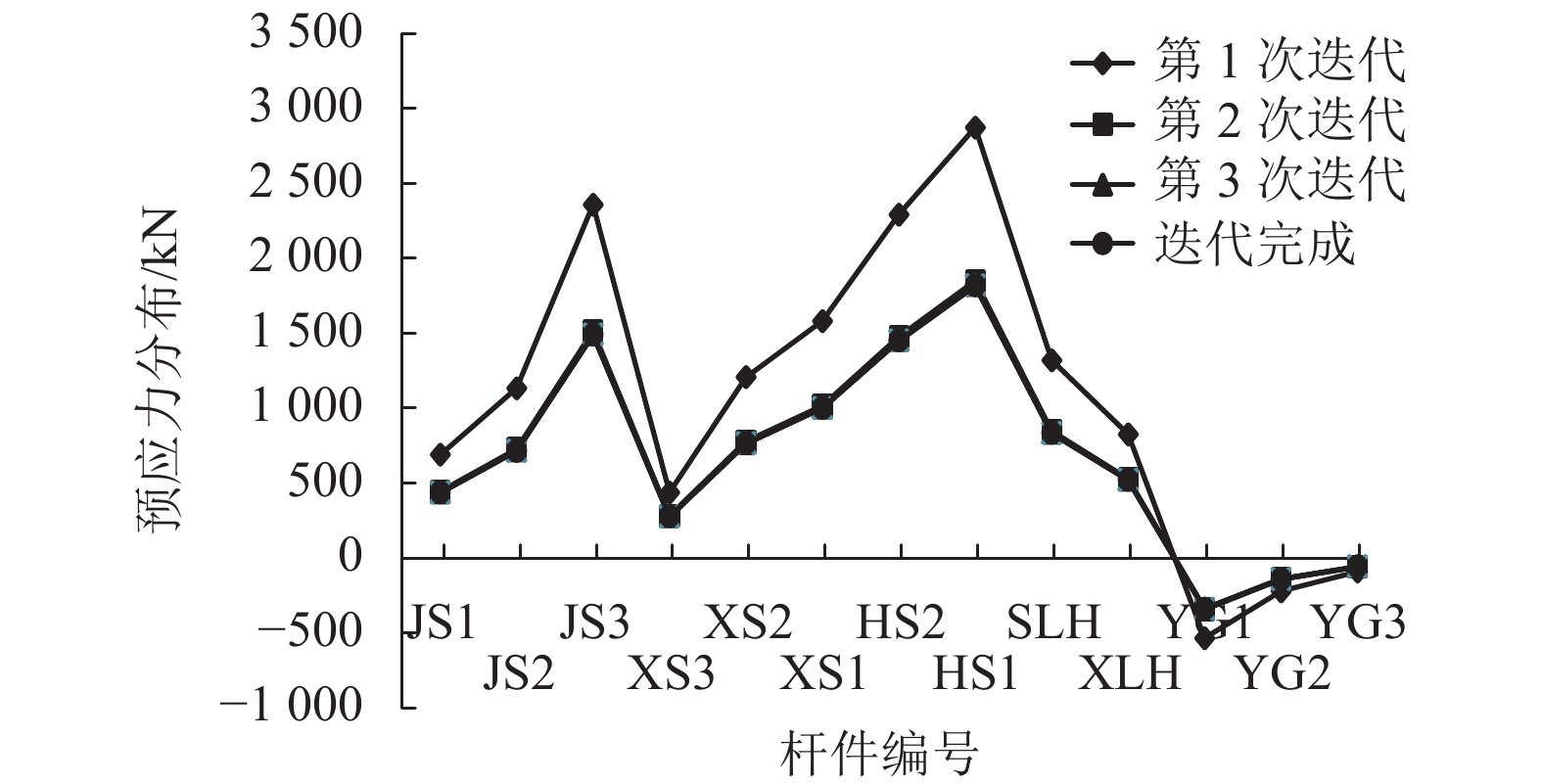
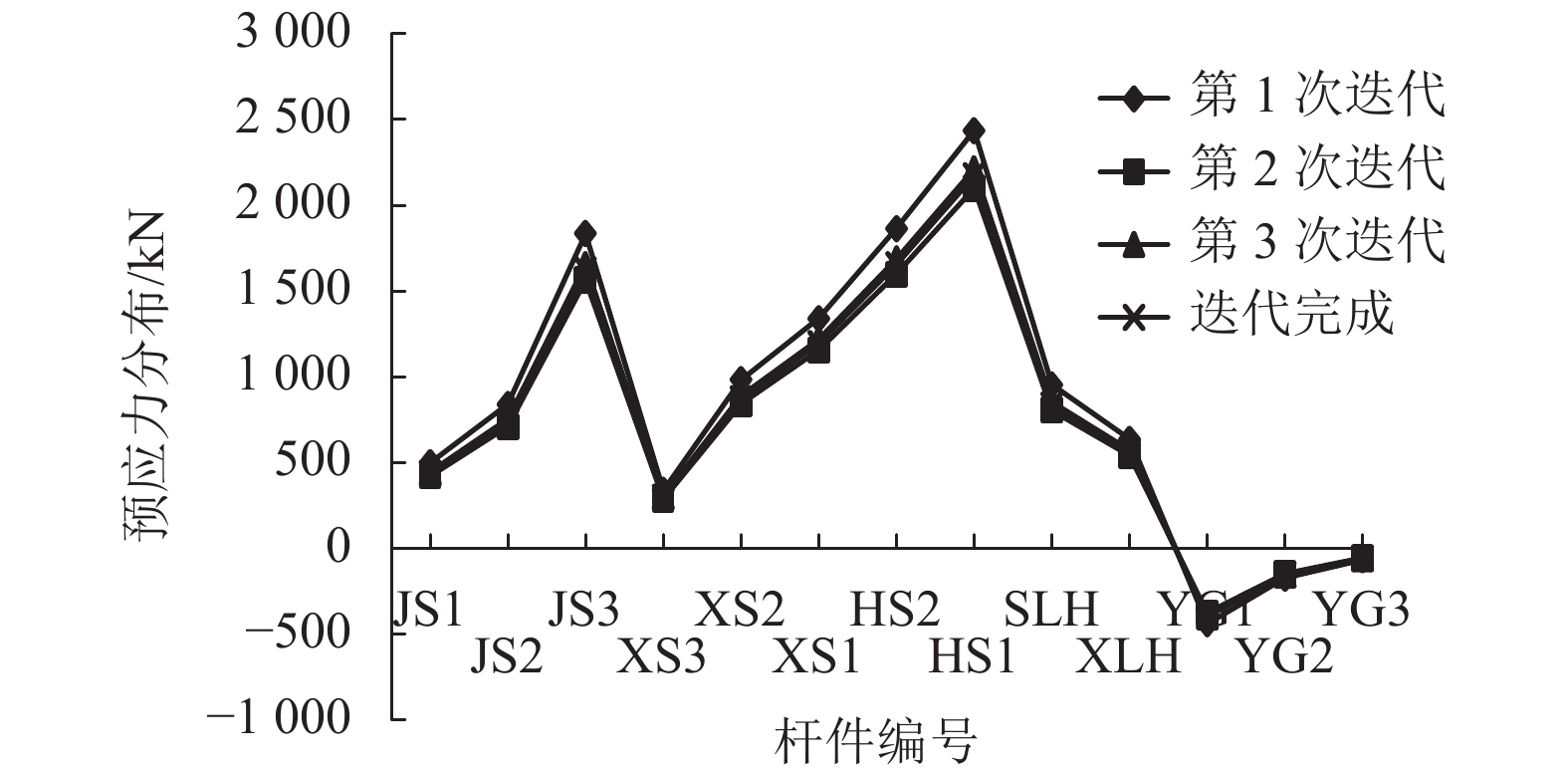
索杆编号	节点编号	不考虑重力影响/kN	考虑重力影响				偏差3/%
索杆编号	节点编号	不考虑重力影响/kN	划分为 1 个单元/kN	偏差1/%	划分为 3 个单元/kN	偏差2/%	偏差3/%
JS1	D	435.33	435.35	0.00	435.19	−0.03	−0.04
JS1	F	435.33	435.35	0.00	435.45	0.03	0.02
JS2	B	715.09	735.73	2.89	735.40	2.84	−0.04
JS2	D	715.09	735.73	2.89	735.97	2.92	0.03
JS3	A	1 491.26	1 619.21	8.58	1 618.81	8.55	−0.02
JS3	B	1 491.26	1 619.21	8.58	1 619.46	8.60	0.02
XS3	D	275.75	296.43	7.50	296.56	7.55	0.04
XS3	G	275.75	296.43	7.50	296.28	7.45	−0.05
XS2	B	764.02	870.19	13.90	870.42	13.93	0.03
XS2	E	764.02	870.19	13.90	869.90	13.86	−0.03
XS1	A	1 000.39	1 193.29	19.28	1 193.83	19.34	0.05
XS1	C	1 000.39	1 193.29	19.28	1 192.67	19.22	−0.05
HS2	E	1 451.14	1 652.77	13.89	1 652.73	13.89	0.00
HS2	E₁	1 451.14	1 652.77	13.89	1 652.73	13.89	0.00
HS1	C	1 818.41	2 169.04	19.28	2 168.97	19.28	0.00
HS1	C₁	1 818.41	2 169.04	19.28	2 168.97	19.28	0.00
SLH	F	833.49	833.50	0.00	833.46	0.00	0.00
SLH	F₁	833.49	833.50	0.00	833.46	0.00	0.00
XLH	G	520.93	559.98	7.50	559.97	7.49	0.00
XLH	G₁	520.93	559.98	7.50	559.97	7.49	0.00
YG1		−338.83	−392.08	−15.72	−392.08	−15.72	0.00
YG2		−140.23	−153.91	−9.76	−153.91	−9.76	0.00
YG3		−57.53	−59.82	−3.98	−59.82	−3.98	0.00
注：偏差1、2 分别表示将每根索段划分为 1 和 3 个单元时，考虑重力影响的找力分析结果与不考虑重力影响的找力分　析结果之间的偏差；偏差 3 表示将每根索段划分为 1 及 3 个单元时，考虑重力影响的找力分析结果之间的偏差；E₁、　C₁、F₁、G₁分别为水平构件 HS2、HS1、SLH、XLH 的另一端.

下载: 导出CSV

参考文献(18)

GEIGER D H. The design and construction of two cable domes for the Korean Olympics[C]// Proceedings of IASS Symposium. Osaka: [s.n.], 1986: 265-272.

LEVY M P. Georgia dome and beyond achieving lightweight-longspan structures[C]// Proceedings of IASS-ASCE International Symposium. Atlanta: [s.n.], 1994: 560-562.

TERRY W R. Georgia dome cable roof construction techniques[C]// Proceedings of IASS-ASCE International Symposium. Atlanta: [s.n.], 1994: 563-572.

曾文平,王元清,张勇,等. 索穹顶结构的预应力设计方法[J]. 工业建筑,2002,32(9): 24-26. doi: 10.3321/j.issn:1000-8993.2002.09.008

ZENG Wenping, WANG Yuanqing, ZHANG Yong, et al. The method of prestress design for cable dome[J]. Industrial Construction, 2002, 32(9): 24-26. doi: 10.3321/j.issn:1000-8993.2002.09.008

陈志华,王小盾,刘锡良. 张拉整体结构的力密度法找形分析[J]. 建筑结构学报,1999,20(5): 29-35.

CHEN Zhihua, WANG Xiaodun, LIU Xiliang. Form finding of tensegrity structures by force density method[J]. Journal of Building Structures, 1999, 20(5): 29-35.

张华,单建. 张拉膜结构的动力松弛法研究[J]. 应用力学学报,2002,19(1): 84-86. doi: 10.3969/j.issn.1000-4939.2002.01.023

ZHANG Hua, SHAN Jian. Dynamic relaxation method study of membrane structures[J]. Chinese Journal of Applied Mechanics, 2002, 19(1): 84-86. doi: 10.3969/j.issn.1000-4939.2002.01.023

刘永福,刘郁馨. 动力松弛法在索杆体系分析中的应用[J]. 南京建筑工程学院学报,1998,46(3): 33-41.

LIU Yongfu, LIU Yuxin. Application of dynamic relaxation in cable-strut systems[J]. Journal of Nanjing Architectural and Civil Engineering Institute, 1998, 46(3): 33-41.

董智力,何广乾,林春哲. 张拉整体结构平衡状态的寻找[J]. 建筑结构学报,1999,20(5): 24-28.

DONG Zhili, HE Guangqian, LIN Chunzhe. Finding of equilibrium states of tensegrity systems[J]. Journal of Building Structures, 1999, 20(5): 24-28.

唐建民,钱若军,蔡新. 索穹顶结构非线性有限元分析[J]. 空间结构,1996,2(1): 12-17.

TANG Jianmin, QIAN Ruojun, CAI Xin. A nonlinear finite element method for analyzing cable domes[J]. Spatial Structures, 1996, 2(1): 12-17.

罗尧治,董石麟. 索杆张力结构初始预应力分布计算[J]. 建筑结构学报,2000,21(5): 59-64. doi: 10.3321/j.issn:1000-6869.2000.05.008

LUO Yaozhi, DONG Shilin. Calculating of initial prestress for cable-strut tensile structures[J]. Journal of Building Structures, 2000, 21(5): 59-64. doi: 10.3321/j.issn:1000-6869.2000.05.008

陈联盟,袁行飞,董石麟. 索杆张力结构自应力模态分析及预应力优化[J]. 土木工程学报,2006,39(2): 11-15. doi: 10.3321/j.issn:1000-131X.2006.02.003

CHEN Lianmeng, YUAN Xingfei, DONG Shilin. Selfstress mode analysis and optimal prestress design of cable-strut tension structures[J]. China Civil Engineering Journal, 2006, 39(2): 11-15. doi: 10.3321/j.issn:1000-131X.2006.02.003

PELLEGRINO S, CALLADINE C R. Matrix analysis of statically and kinematically indeterminate frameworks[J]. International Journal of Solids and Structures, 1986, 22(4): 409-428. doi: 10.1016/0020-7683(86)90014-4

PELLEGRINO S. Structural computation with the singular value decomposition of equilibrium matrix[J]. International Journal of Solids and Structures, 1993, 30(21): 3025-3035. doi: 10.1016/0020-7683(93)90210-X

袁行飞,董石麟. 索穹顶结构整体可行预应力概念及其应用[J]. 土木工程学报,2001,34(2): 33-37. doi: 10.3321/j.issn:1000-131X.2001.02.006

YUAN Xingfei, DONG Shilin. Application of integrity feasible prestressing to tensegrity cable domes[J]. China Civil Engineering Journal, 2001, 34(2): 33-37. doi: 10.3321/j.issn:1000-131X.2001.02.006

阚远,叶继红. 索穹顶结构的找力分析方法——不平衡力迭代法[J]. 应用力学学报,2006,23(2): 250-254. doi: 10.3969/j.issn.1000-4939.2006.02.018

KAN Yuan, YE Jihong. Force finding of tensegrity cable domes —imbalance force iterative method[J]. Chinese Journal of Applied Mechanics, 2006, 23(2): 250-254. doi: 10.3969/j.issn.1000-4939.2006.02.018

张沛,冯健. 一种求解索杆张力结构整体自应力模态的能量方法[J]. 土木工程学报,2013,46(6): 62-68.

ZHANG Pei, FENG Jian. An energy method for overall selfstress modes calculation of cable-strut tension structures[J]. China Civil Engineering Journal, 2013, 46(6): 62-68.

刘小伟. 大跨度索穹顶结构的若干问题研究[D]. 广州: 华南理工大学, 2017.

汤荣伟. 索穹顶结构成形理论及结构优化[D]. 上海: 同济大学, 2005.

施引文献

附加材料(0)

访问统计