Analytical Finite Element for Timoshenko Beams
-
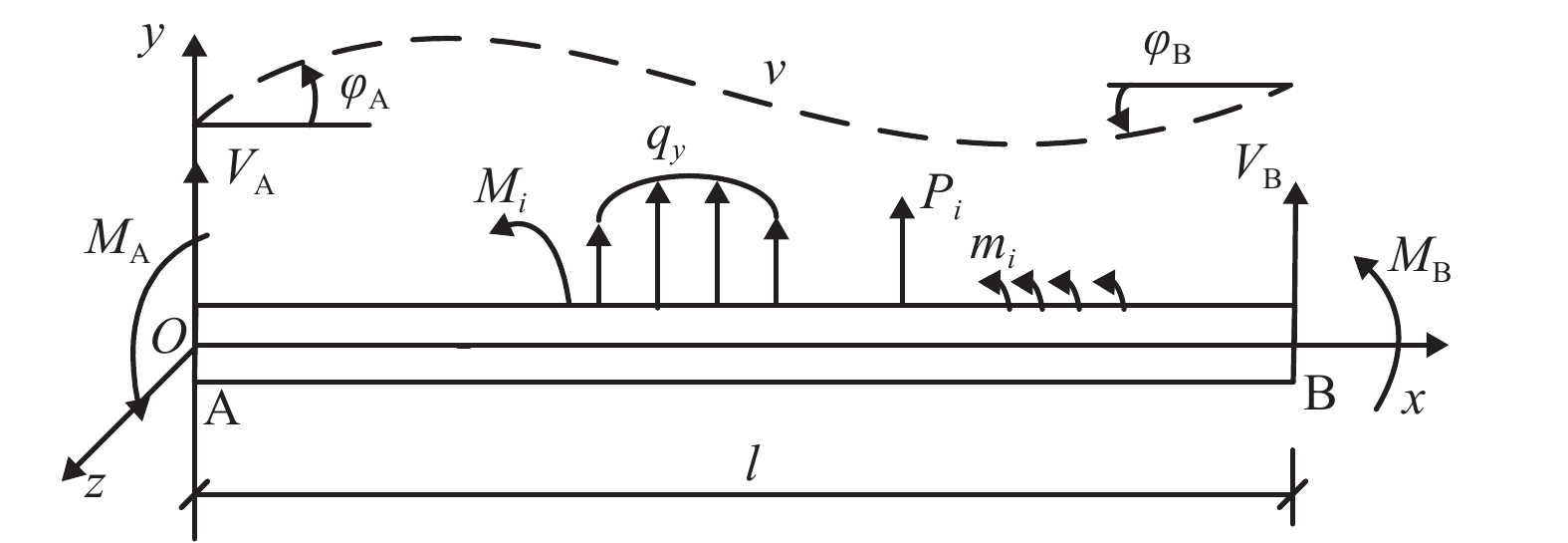
摘要: 为提高深梁结构内力及变形的计算精度和效率,以Timoshenko梁理论为基础,建立了深梁位移控制方程,进而构造了深梁挠度、截面弯曲转角和剪切角的解析位移形函数. 采用势能原理建立了深梁的势能泛函,利用势能变分原理得到了解析型单元列式,进而给出了解析型单元总刚度矩阵,将其与理论解、插值多项式深梁单元进行对比分析. 结果表明:构造的解析型单元只需划分为一个单元即可保证计算的深梁挠度和转角与理论解一致,采用插值多项式单元确定的挠度和转角与理论解的相对误差最大可达到19.785%. 同时,为验证剪切变形对深梁位移影响,将构造的单元与Euler梁单元的计算结果进行对比. 对比表明:对于承受均布荷载作用的悬臂梁,基于Euler梁计算的位移与基于Timoshenko梁理论构造的解析型单元计算的位移偏差可达到50%;对于承受端部集中弯矩作用的简支梁,基于Euler梁计算的位移与基于Timoshenko梁理论构造的解析型单元计算的位移偏差可达到10.769%. 本文构造的单元满足了高精度、高效率的要求;该解析型梁单元可适用于浅梁分析,且不存在剪切闭锁的问题.
-
关键词:
- Timoshenko梁 /
- 解析形函数 /
- 势能原理 /
- 刚度矩阵 /
- 有限元法
Abstract: To improve the calculation accuracy and efficiency of structural force and deformation of deep beams, the deflection control equation of a deep beam was built by Timoshenko beam theory, and analytical displacement shape functions for deflection, section flexural angle and shear angle of deep beam were constructed. Then, potential energy functions for the beam model were established using the potential energy principle; analytical element formulations for beams and the total element stiffness matrix were obtained via the variational principle of potential energy stationary value. Finally, the proposed analytical finite element method was applied to calculate the end deflections of a cantilever deep beam and a simply supported deep beam; and the calculation results were compared with those by theoretical solution and interpolation polynomial method. The results show that the solutions of end deflection and rotation obtained from the proposed analytical element by one element number is in accordance with the theoretical solutions; the maximum relative error between the results calculated from interpolation shape function method and the theoretical solution is 19.785%. To verify the influence of shear deformation on the deflection, the proposed element was also compared with the Euler beam element. The comparison results show that, for cantilever beams subjected to distributed load, the relative error between the results calculated from the Euler beam theory and the proposed element derived by the Timoshenko beam theory is 50%. For simply supported beams subjected to a concentrated bending moment at the end, the relative error is 10.769%. It is proved that the proposed analytical beam element can satisfy the high accuracy and efficiency requirement and avoid shear locking problems. -
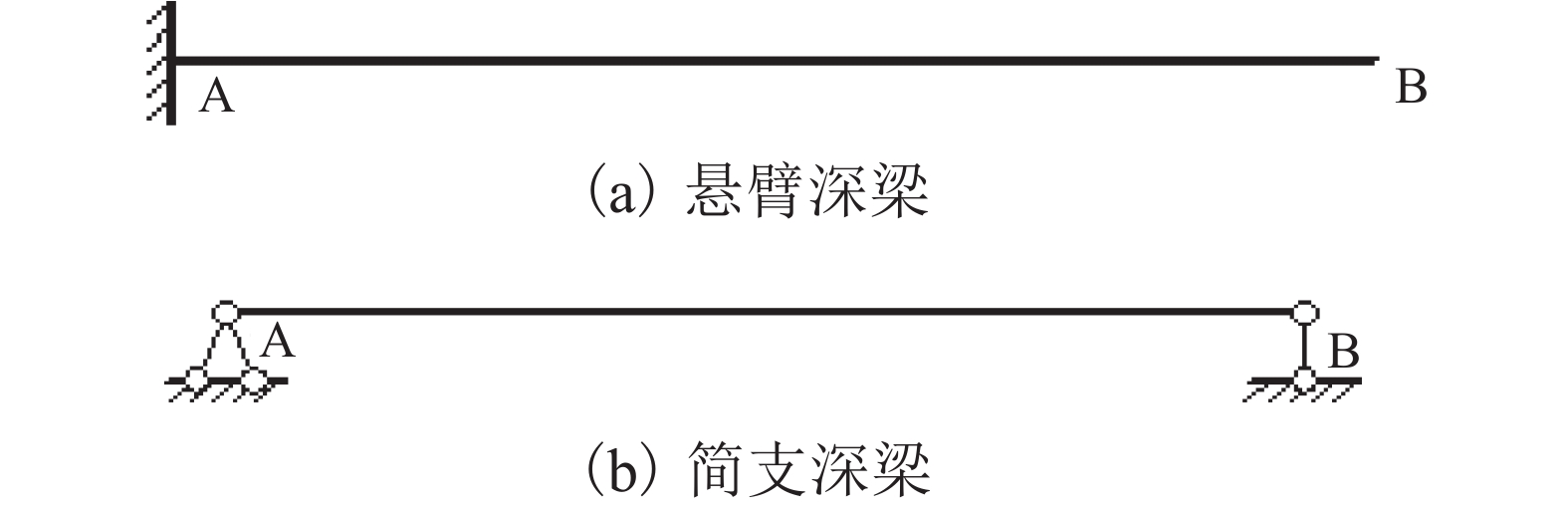
表 1 悬臂梁端部位移计算结果对比
Table 1. Comparisons of end displacement for cantilever beam
类型 项目 均布荷载 右端集中力 右端集中弯矩 νB/(× 10–4 mm) θB/(× 10–4 °) νB/(× 10–4 mm) θB/(× 10–4 °) νB/(× 10–4 mm) θB/(× 10–4 °) 深梁理论解 0.601 071 0.102 857 0.269 643 0.042 943 0.214 286 0.047 619 Timoshenko梁单元 插值形函数法 0.559 734 0.102 856 0.246 678 0.042 857 0.204 275 0.047 600 相对误差/% 6.877 0.001 8.517 0.200 4.672 0.040 解析形函数法 0.601 071 0.102 857 0.269 643 0.042 943 0.214 286 0.047 619 相对误差/% 0 0 0 0 0 0 Euler梁单元 理论解 0.347 140 0.051 429 0.214 290 0.047 619 0.214 290 0.046 190 偏差值/% 42.246 50.000 20.528 10.889 0.002 3.001 表 2 简支梁端部转角计算结果对比
Table 2. Comparisons of end bending angle for simply supported beam
类型 项目 均布荷载 右端集中力 右端集中弯矩 θA/(× 10–4 °) θB/(× 10–4 °) θA/(× 10–4 °) θB/(× 10–4 °) θA/(× 10–4 °) θB/(× 10–4 °) 深梁理论解 0.128 571 –0.128 571 –0.071 649 0.166 446 0.166 446 –0.071 649 Timoshenko梁单元 插值形函数法 0.128 571 –0.128 571 –0.085 825 0.152 270 0.152 270 –0.085 825 相对误差/% 0 0 19.785 8.516 8.516 19.785 解析形函数法 0.128 571 –0.128 571 –0.071 649 0.166 446 0.166 446 –0.071 649 相对误差/% 0 0 0 0 0 Euler梁单元 理论解 0.128 570 –0.128 570 –0.079 365 0.158 730 0.158 730 –0.079 365 偏差值/% 0.001 0.001 10.769 4.636 4.636 10.769 -
古雅琦,王海龙,杨怀宇. 一种大变形几何非线性Euler-Bernoulli梁单元[J]. 工程力学,2016,30(6): 11-15.GU Yaqi, WANG Hailong, YANG Huaiyu. A lagre deformation geometric nonlinear Euler-Bernoulli beam element[J]. Engineering Mechanics, 2016, 30(6): 11-15. 夏拥军,陆念力. 梁杆结构稳定性分析的高精度Euler-Bernoulli梁单元[J]. 沈阳建筑大学学报(自然科学版),2006,22(3): 362-366.XIA Yongjun, LU Nianli. A new Euler-Bernoulli beam element with high accuracy for the stability analysis of beam structures[J]. Journal of Shenyang Jianzhu University (Natural Science), 2006, 22(3): 362-366. 夏拥军,缪谦. Euler-Bernoulli梁单元的完整二阶位移场[J]. 中国工程机械学报,2011,9(4): 416-420.XIA Yongjun, MIAO Qian. Complete second-order displacement field of Euler-Bernoulli beam element[J]. Chinese Journal of Construction Machinery, 2011, 9(4): 416-420. SCHNABL S, SAJE M, TURK G, et al. Locking-free two-layer Timoshenko beam element with interlayer slip[J]. Finite Elements in Analysis and Design, 2007, 43(9): 705-714. SCHNABL S, SAJE M, TURK G, et al. Analytical solution of two-layer beam taking into account interlayer slip and shear deformation[J]. Journal of Structural Engineering, 2007, 133(6): 886-894. OWEN D R J, HINTON E. Finite elements in plasticity-theory and practice[M]. New York: Swansea Pineridge Press, 1980: 1-50 TIMOSHENKO S P. On the correction for shear of the differential equation for transverse vibrations of prismatic bars[J]. The London,Edinburgh,and Dublin Philosophical Magazine and Journal of Science, 1921, 41(6): 744-746. HUTCHINSON J R. Shear coefficients for Timoshenko beam theory[J]. Transactions-American Society of Mechanical Engineers Journal of Applied Mechanics, 2001, 68(1): 87-92. 王乐,王亮. 一种新的计算Timoshenko梁截面剪切系数的方法[J]. 应用数学和力学,2013,34(7): 756-763.WANG Le, WANG Liang. A new method of obtaining Timoshenko’s shear coefficients[J]. Applied Mathematics and Mechanics, 2013, 34(7): 756-763. CLOUGH R W. The finite element method in plane stress analysis[C]//Proceeding of 2nd ASCE Conference on Electronic Computation. Pittsburg: [s.n.], 1960: 112-125 SHEIKH A H. New concept to include shear deformation in a curved beam element[J]. Journal of Structural Engineering,ASCE, 2002, 128(3): 406-410. ORAL S. Anisoparametric interpolation in hybrid-stress Timoshenko beam element[J]. Journal of Structural Engineering,ASCE, 1991, 117(4): 1070-1078. 李潇,王宏志,李世萍,等. 解析型Winkler弹性地基梁单元构造[J]. 工程力学,2015,32(3): 66-72.LI Xiao, WANG Hongzhi, LI Shiping, et al. Element for beam on Winkler elastic foundation based on analytical trial functions[J]. Engineering Mechanics, 2015, 32(3): 66-72. 李世萍. 解析型弹性地基梁单元构造[D]. 北京: 中国农业大学, 2013 罗双. 解析型Pasternak弹性地基梁单元构造[D]. 北京: 中国农业大学, 2016 李静. 解析型双参数弹性地基Timoshenko梁单元构造[D]. 北京: 中国农业大学, 2017 龙驭球, 包世华. 结构力学教程(Ⅱ)[M]. 北京: 高等教育出版社, 2006: 2-8, 56-60 李世尧. 解析型Timoshenko梁单元构造[D]. 北京: 中国农业大学, 2017 -




 下载:
下载: