Static Pushover Analysis of Frame Structure Based on Force Analogy Method
-
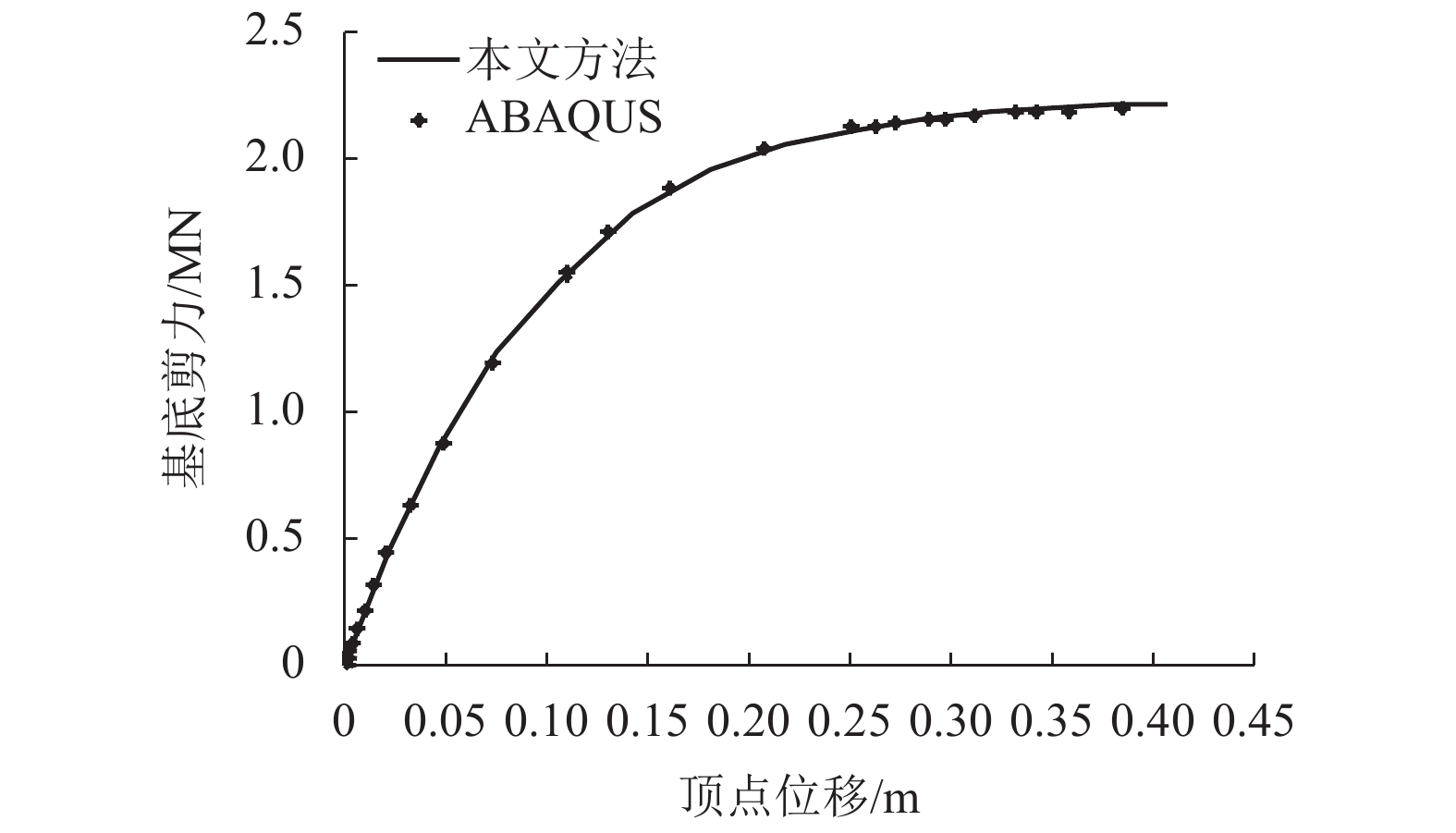
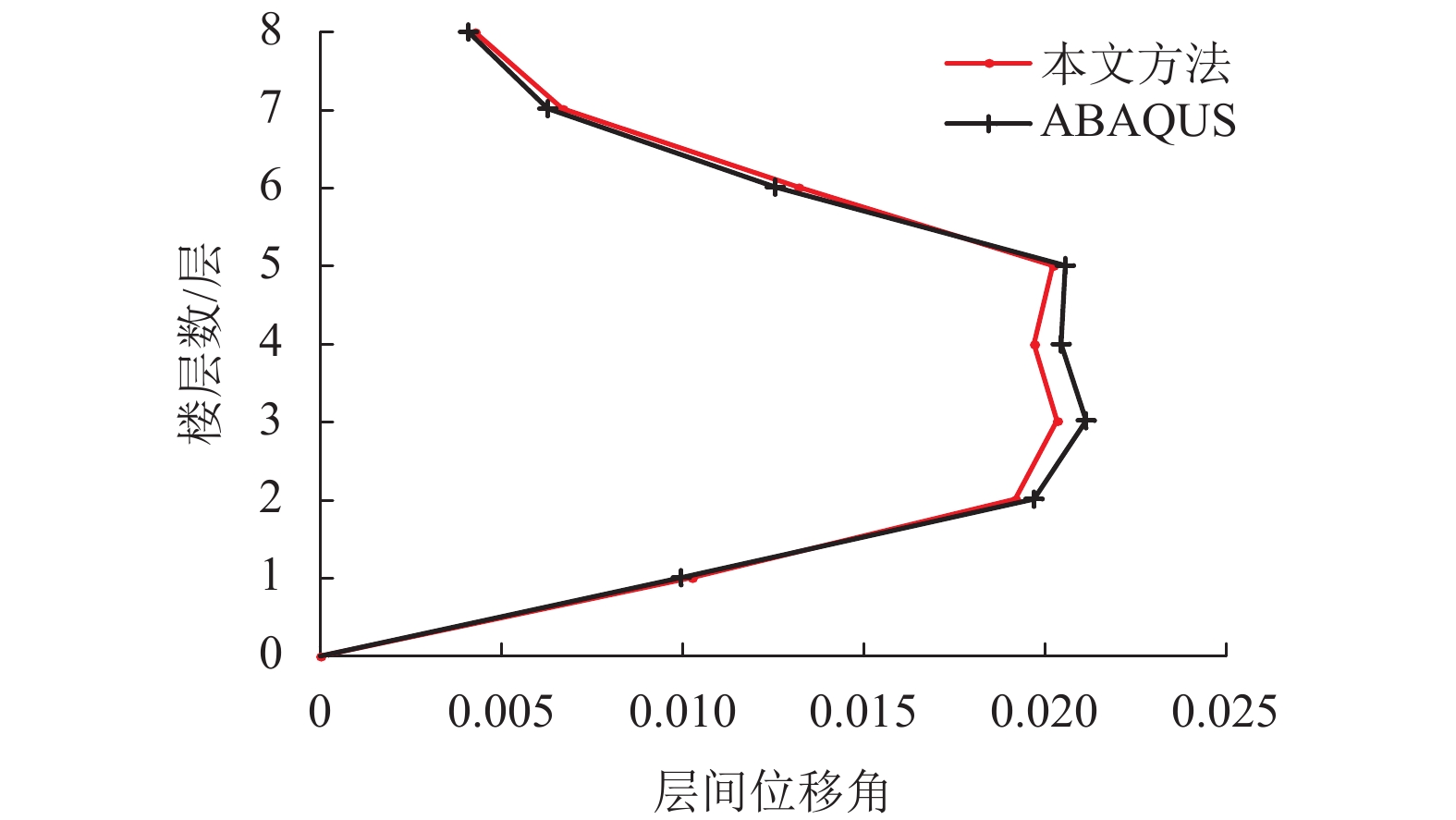
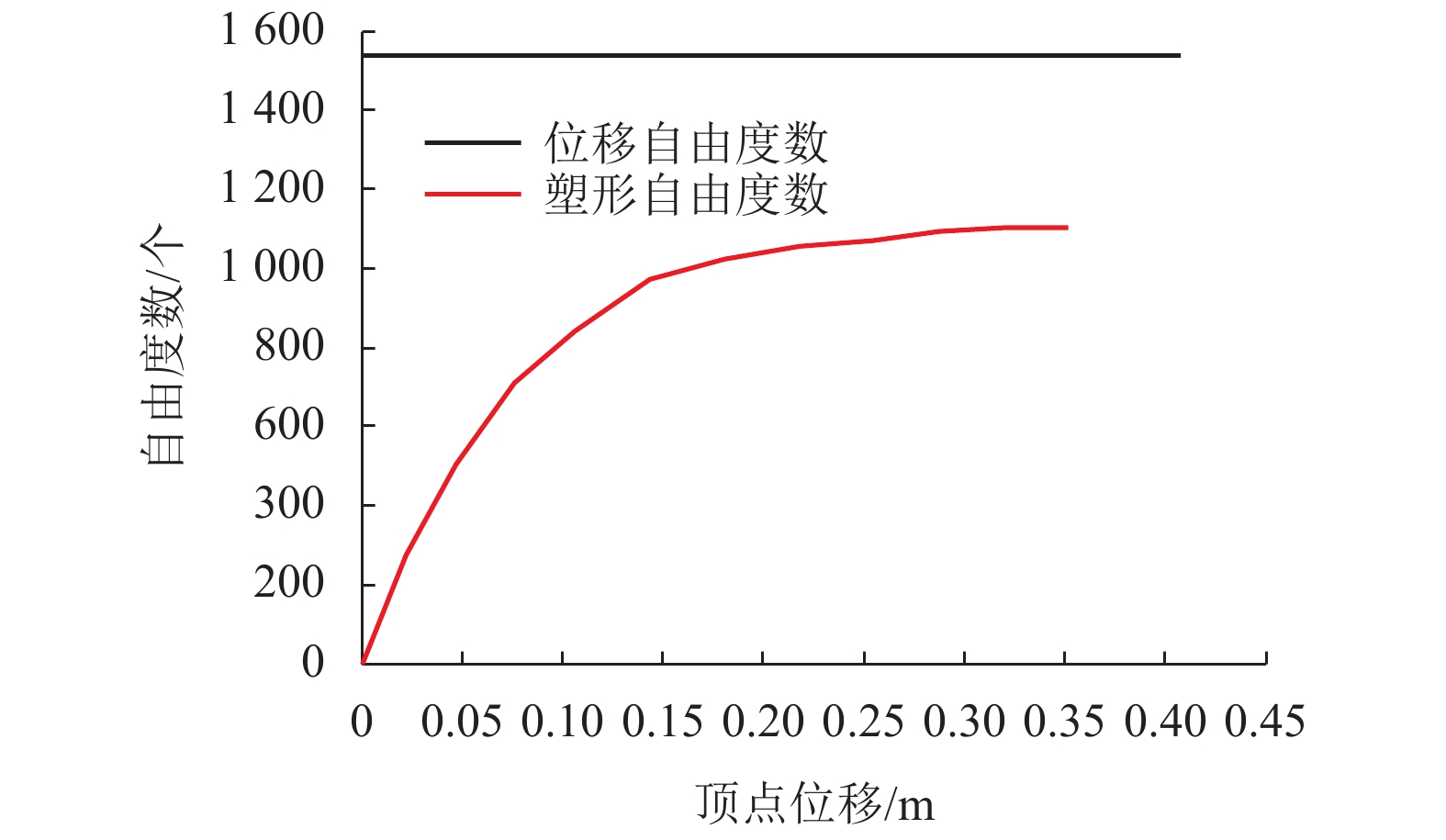
摘要: 传统静力推覆分析方法求解结构非线性变形需对结构整体刚度矩阵进行实时地合成与分解，该过程将占用大量计算资源.基于拟力法的纤维梁有限元分析方法进行静力推覆分析，在迭代求解结构非线性变形时，首先对弹性刚度矩阵进行分解，计算出侧向荷载作用下的弹性位移；然后通过反复调用弹性刚度矩阵的分解结果与弹性位移，减少回代计算量；最后采用算法时间复杂度理论定量对比了该方法与传统方法的计算效率，通过一榀八层钢筋混凝土框架结构数值算例，分析比较了两种方法的计算结果与算法时间复杂度. 结果表明：两种方法顶点位移-基底剪力曲线基本吻合，层间位移角与楼层之间的关系曲线也基本一致，两者的最大误差出现在第3层，为3.72%，与传统方法相比，基于拟力法的静力推覆分析方法算法时间复杂度降低了80%，计算效率至少是传统方法的5倍.Abstract: In traditional pushover analysis, solving nonlinear deformation need to update and decompose global stiffness matrix in real time, which costs many computing resources. The static pushover analysis for nonlinear fiber beam element is conducted on the basis of the force analogy method (FAM). Firstly, the elastic displacement under the lateral load was calculated by the factorization of elastic stiffness matrix before the iteration of nonlinear deformation. Secondly, the computational cost of back iteration was decreased by utilizing the factorization result of elastic stiffness matrix and elastic displacement during iterations. Finally, the algorithm complexity theory was utilized to evaluate the efficiency of the proposed algorithm and a classical method. The computational results and algorithm time complexity of the two methods were compared through a numerical results of 2D eight-floor frame structure. Results show that with two methods the vertex displacement-base shear curve basically coincides as well as the story drift curve, and the maximum error of story drift is on the 3rd floor with 3.72%. Compared with the traditional method, the algorithm complexity of the proposed method is decreased about 80%, and its computing efficiency is increased at least five times.
-
图 1 基于拟力法的静力推覆分析流程
Figure 1. Flow chart for static pushover analysis based on force analogy method
图 5 塑性自由度数与顶点位移关系
Figure 5. Relationship between number of plastic degrees and roof displacement
表 1 时间复杂度
Table 1. Time complexity
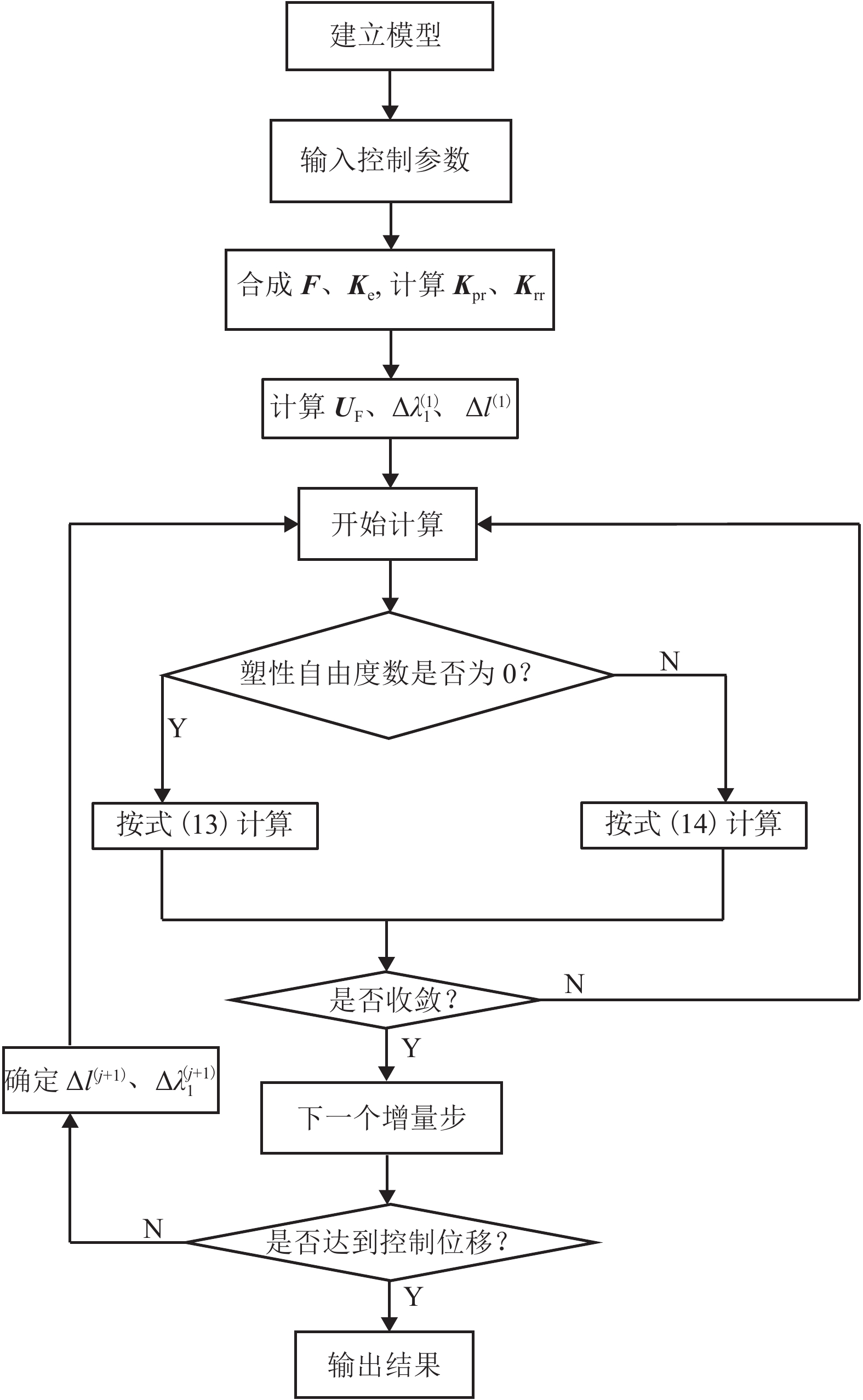
计算步骤 计算项目 时间复杂度 1 $\left( {\Delta { {{X} }_1} } \right)_1^{\left( j \right)} = \Delta \lambda _1^{\left( j \right)}{ {{U} }_{\rm{F} } }$ $n$ 2 $\Delta { {{u} }_0} = \left( { {{K} }_{ {\rm{pr} } }^{\rm{T} } } \right)_1^{\left( j \right)}{\left( {\Delta { {{X} }_1} } \right)^{\left( j \right)} }$ $2\alpha d - d$ 3 $\left( {{{{K}}_{{\rm{pl}}}}} \right)_1^{\left( j \right)} = \left( {{{{K}}_{{\rm{rr}}}}} \right)_1^{\left( j \right)} - \left( {{{K}}_{{\rm{pr}}}^{\rm{T}}} \right)_1^{\left( j \right)}{{K}}_{\rm{e}}^{ - 1}\left( {{{{K}}_{{\rm{pr}}}}} \right)_1^{\left( j \right)}$ $\beta d/2$ 4 $\Delta {{{u}}_1} = \left( {{{K}}_{{\rm{pl}}}^{ - 1}} \right)_1^{\left( j \right)}\Delta {{{u}}_0}$ $m_{\rm{d}}^2d + 8{m_{\rm{d}}}d + d$ 5 $\Delta {{{u}}_2} = \left( {{{{K}}_{{\rm{pr}}}}} \right)_1^{\left( j \right)}\Delta {{{u}}_1}$ $2\alpha d - d$ 6 $\left( {\Delta { {{X} }_2} } \right)_1^{\left( j \right)} = {{K} }_{\rm{e} }^{ - 1}\Delta { {{u} }_2}$ $2mn - n - {m^2}/2 + 1/2$ 7 $\left( {\Delta {{X} } } \right)_1^{\left( j \right)} = \left( {\Delta { {{X} }_1} } \right)_1^{\left( j \right)} + \left( {\Delta { {{X} }_2} } \right)_1^{\left( j \right)}$ $n$ 
下载: 导出CSV
表 2 截面配筋
Table 2. Parameters of sections
楼层 梁 中柱 边柱 截面的宽，高/mm 配筋/mm2 截面的宽，高/mm 配筋/mm2 截面的宽，高/mm 配筋/mm2 1 $300,\;600$ 6874 $700 ,\;700$ 8758 $700 ,\;700$ 11235 2 $300 ,\;600$ 6874 $700 ,\;700$ 5024 $700 ,\;700$ 5024 3 $300 ,\;600$ 6874 $700 ,\;700$ 5024 $700 ,\;700$ 5024 4 $300 ,\;600$ 6874 $700 ,\;700$ 5024 $700 ,\;700$ 5024 5 $300 ,\;600$ 4688 $600 ,\;600$ 3786 $600 ,\;600$ 3786 6 $300 ,\;600$ 4688 $600 ,\;600$ 3786 $600 ,\;600$ 3786 7 $300 ,\;600$ 4688 $600 ,\;600$ 3786 $600 ,\;600$ 3786 8 $300 ,\;600$ 4688 $600 ,\;600$ 3786 $600 ,\;600$ 3786 注：配筋指截面中钢筋截面面积.
下载: 导出CSV
-
FREEMAN S A, NICOLETTI J P, TYRELL J V. Evaluation of existing buildings for seismic risk—a case study of puget sound naval shipyard[C]//Proceedings of 1st U.S. National Conference on Earthquake Engineering. Berkeley: Earth quake Engineering Research Institution, 1975: 113-122. 陆新征, 蒋庆, 缪志伟, 等. 建筑抗震弹塑性分析[M]. 2版. 北京: 中国建筑工业出版社, 2015: 84-85. 韩建平,吕西林,李慧. 基于性能的地震工程研究的新进展及对结构非线性分析的要求[J]. 地震工程与工程振动,2007,27(4): 15-23. doi: 10.3969/j.issn.1000-1301.2007.04.003HAN Jianping, LÜ Xinlin, LI Hui. State of the art of performance based earthquake engineering and need for structural nonlinear analysis[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(4): 15-23. doi: 10.3969/j.issn.1000-1301.2007.04.003 SAIIDI M, SOZEN M A. Simple nonlinear seismic analysis of R/C structures[J]. Journal of Structural Division (ASCE), 1981, 107(5): 937-951. FAIFAR P, GASPERSIC P. The N2 method for seismic damage analysis of RC buildings[J]. Earthquake Enginerring & Structure Dynamics, 1996, 25(1): 31-46. KRAWINKLER H, SENEVIRATNA G D P K. Pros and cons of a pushover analysis of seismic performance evaluation[J]. Engineering Structures, 1998, 20(4): 452-464. CHOPRA A K, GOEL R K. A modal pushover analysis procedure for estimating seismic demands for buildings[J]. Earthquake Engineering & Structure Dynamics, 2002, 31(3): 561-582. GUPTA B, EERI M, KUNNATH S K. Adaptive spectra-based pushover procedure for seismic evaluation of structres[J]. Earthquake Spectra, 2000, 16(2): 367-391. doi: 10.1193/1.1586117 欧进萍,侯钢领,吴斌. 概率Pushover分析方法及其在结构体系抗震可靠度评估中的应用[J]. 建筑结构学报,2001,22(6): 81-86. doi: 10.3321/j.issn:1000-6869.2001.06.013OU Jinping, HOU Gangling, WU Bin. Random pushover analysis method and its application in earthquake-resistant reliability evaluation of structural systems[J]. Journal of Building Structures, 2001, 22(6): 81-86. doi: 10.3321/j.issn:1000-6869.2001.06.013 朱杰江,吕西林,容柏生. 复杂体型高层结构的推覆分析方法和应用[J]. 地震工程与工程振动,2003,23(2): 26-36. doi: 10.3969/j.issn.1000-1301.2003.02.005ZHU Jiejiang, LÜ Xilin, RONG Baisheng. Pushover analysis method and its application to RC tall building with complex structural type[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(2): 26-36. doi: 10.3969/j.issn.1000-1301.2003.02.005 黄羽立,陆新征,叶列平,等. 基于多点位移控制的推覆分析算法[J]. 工程力学,2011,28(2): 18-23.HUANG Yuli, LU Xinzheng, YE Lieping, et al. A pushover analysis algorithm based on multiple point constrains[J]. Engineering Mechanics, 2011, 28(2): 18-23. LIN T H. Theory of inelastic structures[M]. New York: John Wiley & Sons, 1968: 43-45. WONG K K F, YANG R. Inelastic dynamic response of structures using force analogy method[J]. Journal of Engineering Mechanics, 1999, 125(10): 1190-1199. doi: 10.1061/(ASCE)0733-9399(1999)125:10(1190) 李钢,刘啟凤,李宏男. 基于拟力法的MBC非线性控制[J]. 振动工程学报,2010,23(3): 324-332. doi: 10.3969/j.issn.1004-4523.2010.03.014LI Gang, LIU Qifeng, LI Hongnan. MBC nonlinear control strategy based on force analogy method[J]. Journal of Vibration Engineering, 2010, 23(3): 324-332. doi: 10.3969/j.issn.1004-4523.2010.03.014 ZHANG Xin, WONG K K F, WANG Yi. Performance assessment of moment resisting frames during earthquake based on the force analogy method[J]. Engineering structures, 2007, 29(10): 2792-2802. 李钢,李宏男,李瀛. 基于拟力法的消能减震结构地震反应分析[J]. 土木工程学报,2009,42(4): 55-63. doi: 10.3321/j.issn:1000-131X.2009.04.008LI Gang, LI Hongnan, LI Ying. Analysis of seismic response of structures with dissipation devices by using fictitious force method[J]. Engineering Structures, 2009, 42(4): 55-63. doi: 10.3321/j.issn:1000-131X.2009.04.008 LI G, LI H. Seismic response analysis of structure with energy dissipation devices using force analogy method[J]. Structure Design of Tall & Special Buildings, 2011, 20(3): 291-313. 李钢,余丁浩,李宏男. 基于拟力法的纤维梁有限元非线性分析方法[J]. 建筑结构学报,2016,37(9): 61-68.LI Gang, YU Dinghao, LI Hongnan. Nonlinear fiber beam element analysis based on force analogy method[J]. Journal of Building Structures, 2016, 37(9): 61-68. HAGER W W. Updating the inverse of a matrix[J]. Siam Review, 1989, 31(31): 221-239. 何政, 欧进萍. 钢筋混凝土结构非线性分析[M]. 哈尔滨: 哈尔滨工业大学出版社, 2006: 188-194 王晓东. 计算机算法设计与分析[M]. 3版. 北京: 电子工业出版社, 2007: 1-5. 李钢,贾硕,李宏男. 基于算法复杂度理论的拟力法计算效率评价[J]. 计算力学学报,2018,35(2): 129-137. doi: 10.7511/jslx20170124001LI Gang, JIA Shuo, LI Hongnan. The efficiency evaluation of force analogy method based on the algorithm complexity theory[J]. Chinese Journal of Computational Mechanics, 2018, 35(2): 129-137. doi: 10.7511/jslx20170124001 KIRSCH U. Reanalysis of structures: a unified approach for linear, nonlinear, static and dynamic systems[M]. New York: Springer Publishing Company, 2008: 266-269. GOLUBG H, VAN LOAN C F. Matrix computations[M]. Forth Edition. Beijing: Posts & Telecom Press, 2014: 12-13. KENT D C. Inelastic behaviour of reinforced concrete members with cyclic loading[D]. Christchurch: University of Canterbury, 1969. YASSIN M H M. Nonlinear analysis of prestressed concrete structures under monotonic and cyclic loads[D]. California: University of California, Berkeley, 1994. 侯爽,欧进萍. 结构Pushover分析的侧向力分布及高阶振型影响[J]. 地震工程与工程振动,2004,24(3): 89-97. doi: 10.3969/j.issn.1000-1301.2004.03.012HOU Shuang, OU Jinping. A study of load pattern selection of pushover analysis and influence of higher modes[J]. Earthquake Engineering and Engineering Vibration, 2004, 24(3): 89-97. doi: 10.3969/j.issn.1000-1301.2004.03.012 门进杰,史庆轩,周琦. 框架结构基于性能的抗震设防目标和性能指标的量化[J]. 土木工程学报,2008,41(9): 76-82. doi: 10.3321/j.issn:1000-131X.2008.09.012MEN Jinjie, SHI Qingxuan, ZHOU Qi. Performance-based seismic fortification criterion and quantified performance index for reinforced concrete frame structures[J]. China Civil Engineering Journal, 2008, 41(9): 76-82. doi: 10.3321/j.issn:1000-131X.2008.09.012 -
下载:
点击查看大图
图(5) / 表(2)
计量
- 文章访问数: 672
- HTML全文浏览量: 434
- PDF下载量: 23
- 被引次数: 0