Shaking Table Test of Model Structure with Viscous Dampers Subjected to Random Earthquake Ground Motions
-
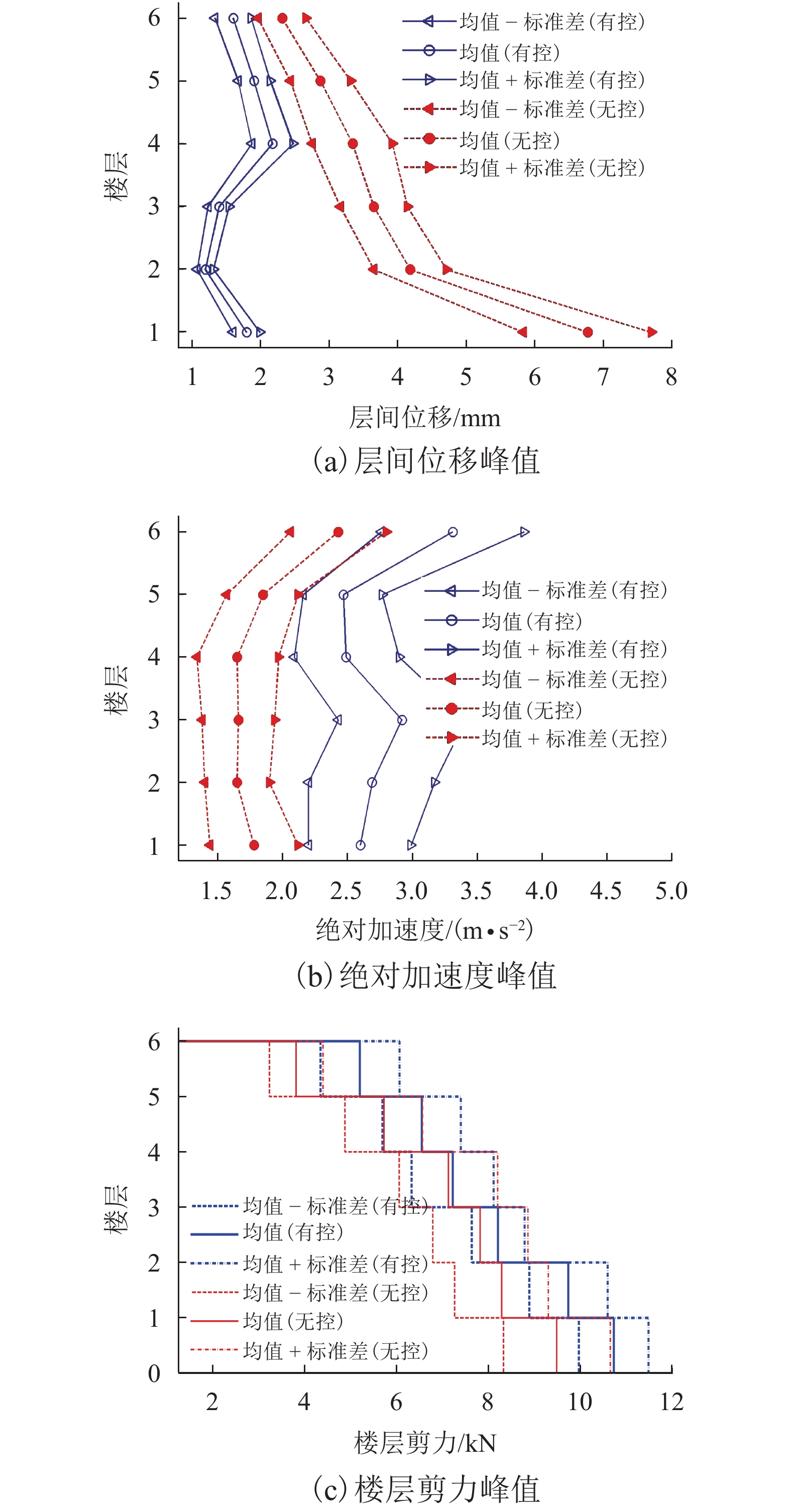
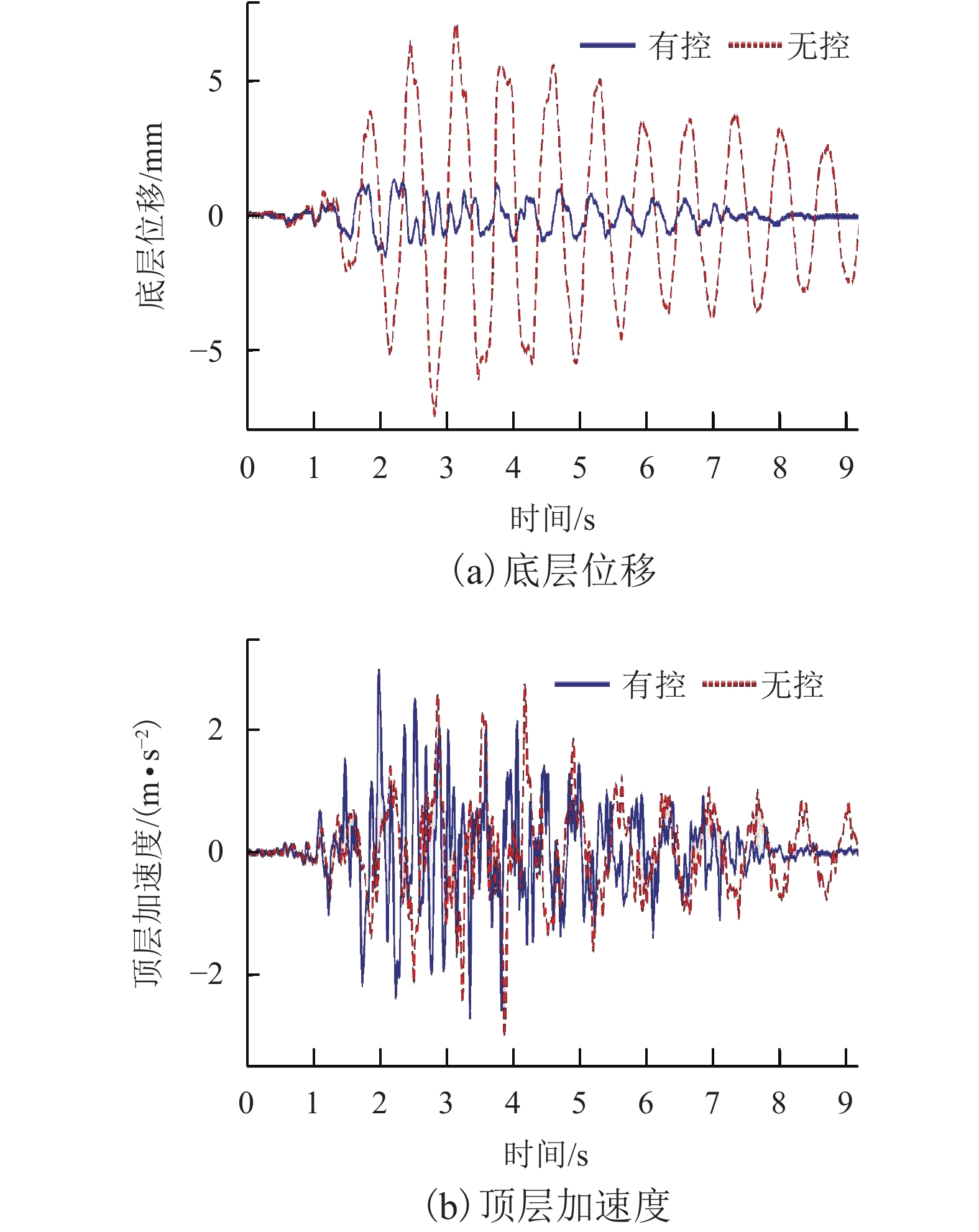
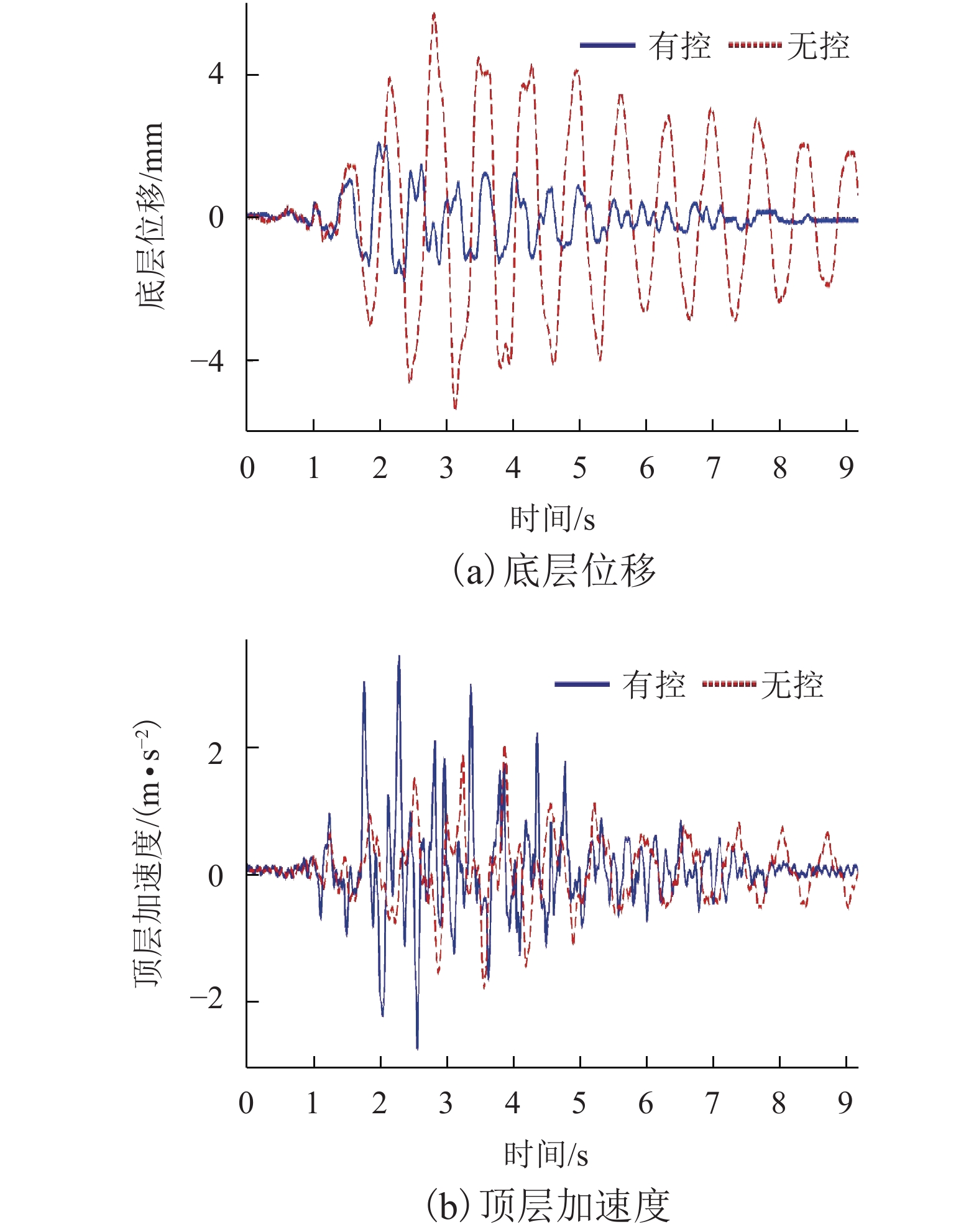
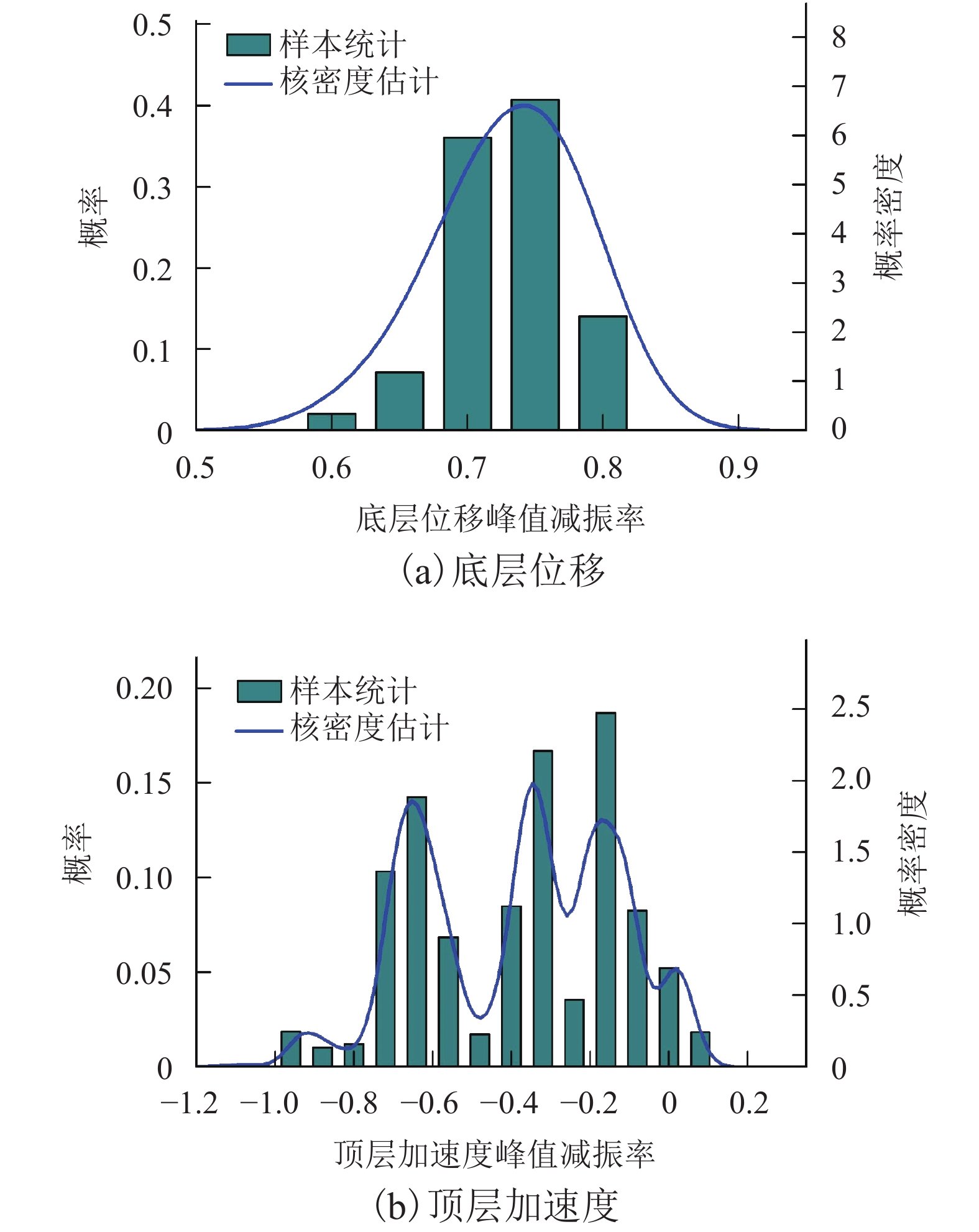
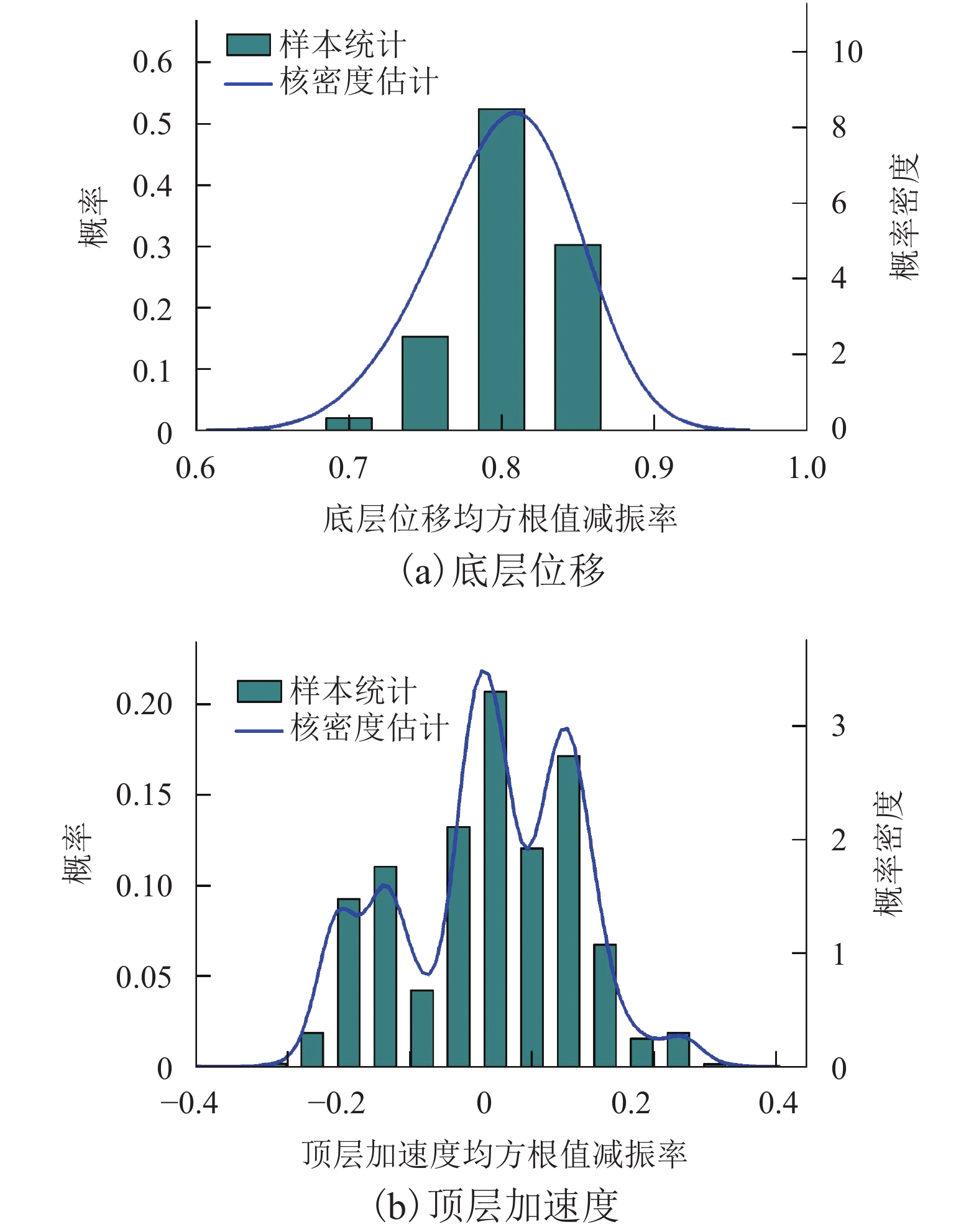
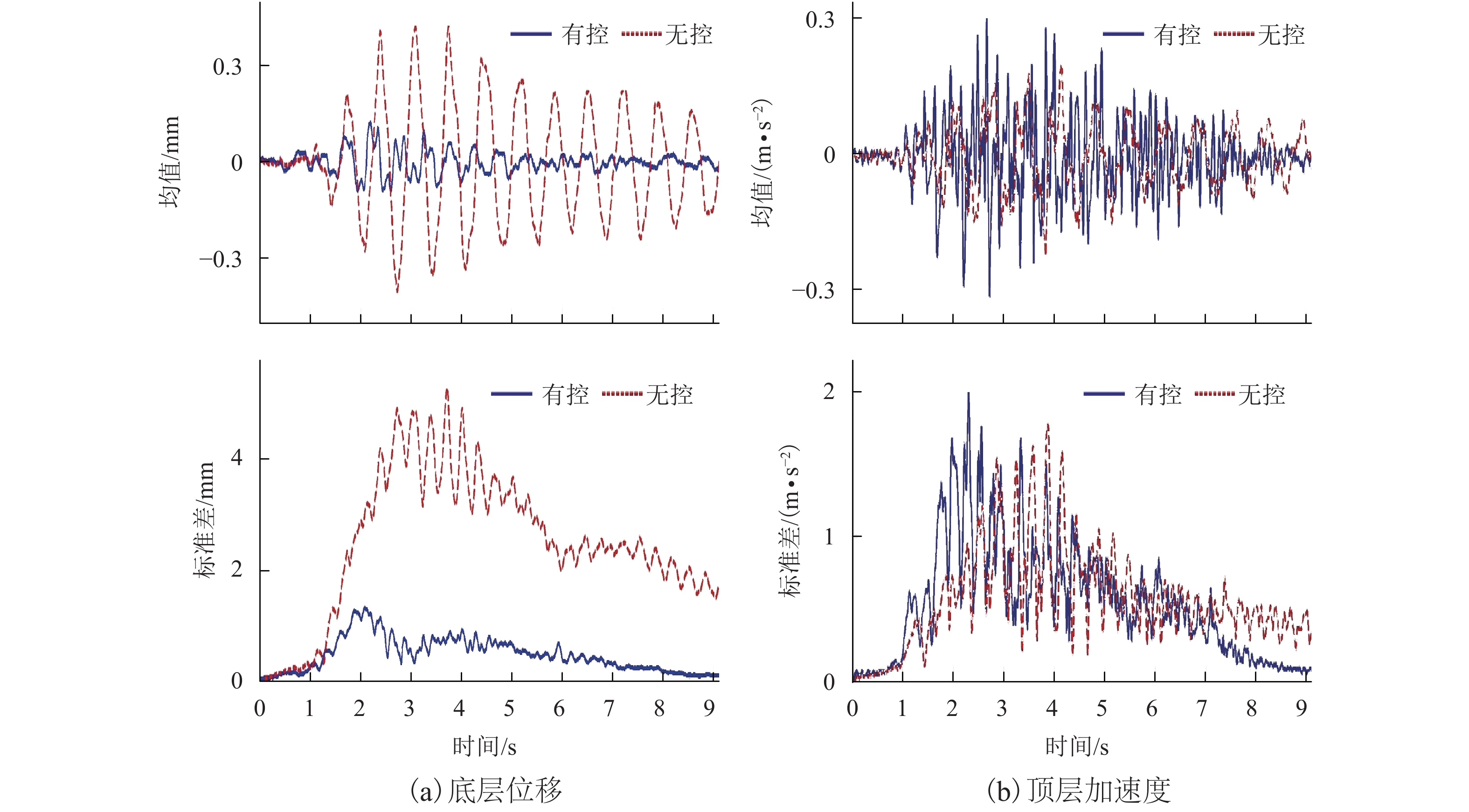
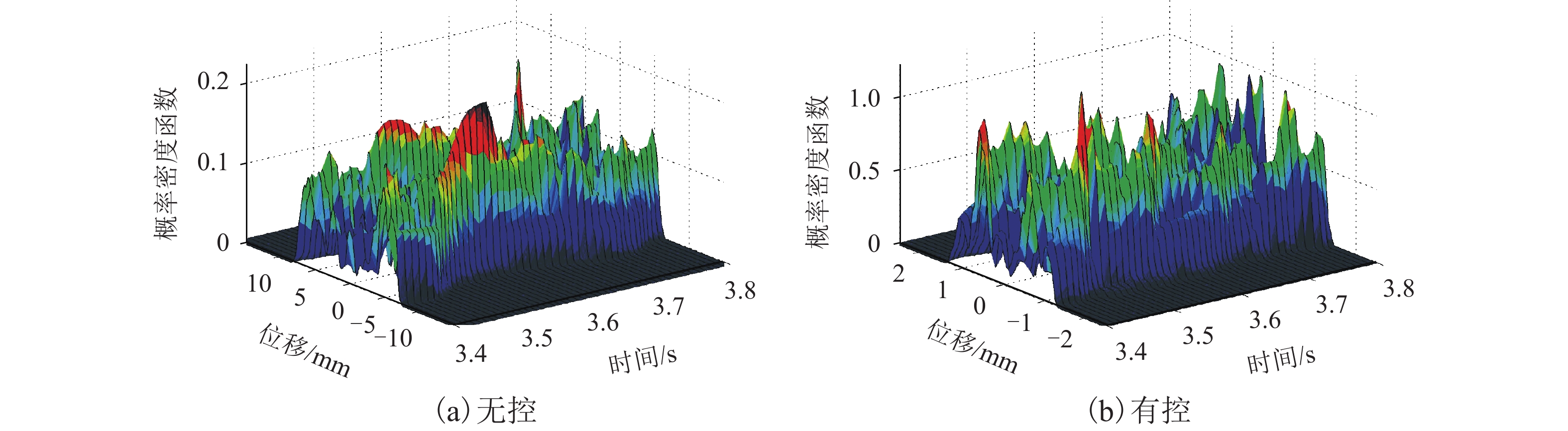
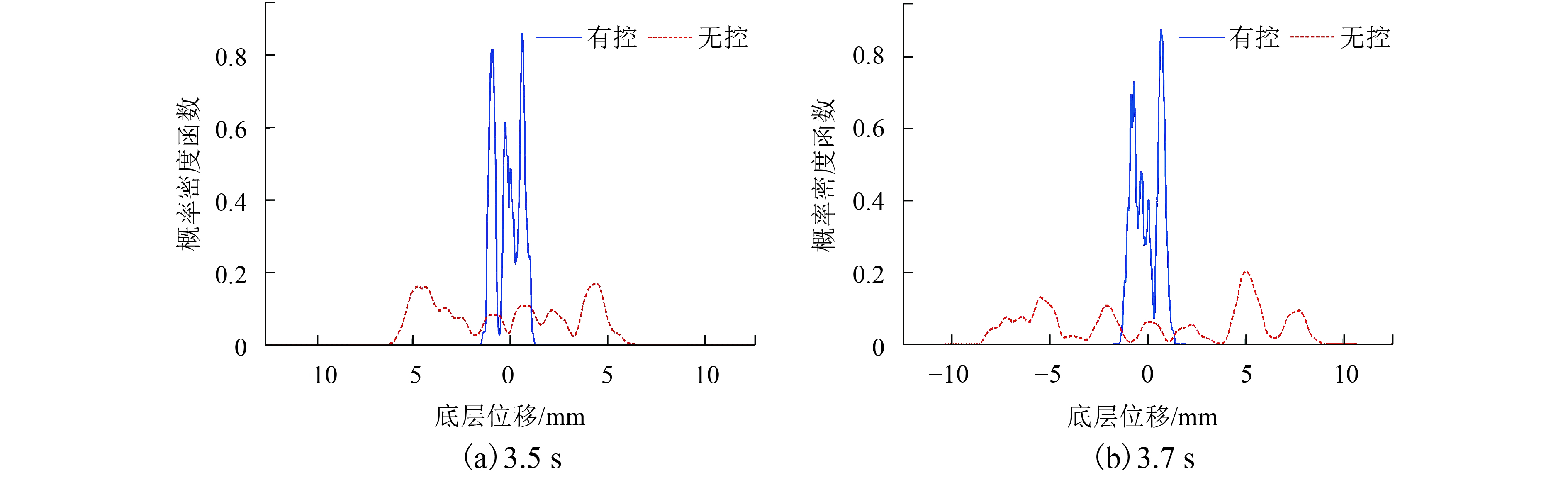
摘要: 为研究随机激励作用时粘滞阻尼器在结构中的实际减振效果，开展了随机地震动作用下粘滞阻尼减震结构振动台试验研究. 振动台试验中，采用基于物理随机地震动模型生成的地震动样本作为台面输入. 通过对有控和无控模型结构响应的均值、标准差以及概率密度函数等进行比较，系统分析了粘滞阻尼器的消能减震效果. 结果表明：有控模型结构层间位移响应显著减小，楼层剪力均方根值取得一定的减振效果，而大多数楼层绝对加速度响应出现不同程度增大；随机地震动作用下模型结构动力响应的变异性显著，且不同试验地震动样本输入时粘滞阻尼器取得的减振效果不同；粘滞阻尼器-钢支撑系统工作时能给被控结构提供一定的附加刚度和附加阻尼，使得结构动力特性产生变化，进而改变结构地震响应；有控模型结构底层位移响应的均值及标准差在地震动作用时段内均显著减小，且底层位移响应在各时刻的概率密度函数的分布宽度及其形态较无控时发生明显变化.Abstract: To investigate the control efficiency of structures installed with viscous dampers subjected to random excitations, shaking table tests on vibration control of a randomly base-driven structure with and without dampers, were conducted. In the experiments, the base excitation was represented by a physical stochastic ground motion model. By comparing the probabilistic characteristics of the responses of the controlled and uncontrolled structures, such as the mean, standard deviation, and the probability density function, the seismic mitigation effect of viscous dampers was systematically analysed. The results show that the interstory drifts of the controlled structure are obviously smaller than those in the uncontrolled cases, and interstory shear forces are reduced to some extent in the root-mean-square sense, while absolute accelerations of most floors increase to different degrees. It was also found that the variability of dynamic responses of the model structure subjected to random earthquake ground motions is very significant, and the control efficiency is different when various representative time histories of ground accelerations are adopted as seismic inputs. Moreover, the working viscous damper-steel support system can provide additional stiffness and damping to the controlled structure, and thus make the structural dynamic characteristics change, which leads to a change in the structural seismic response. Finally, the mean and standard deviation of the bottom floor displacements of the controlled structure are considerably mitigated throughout the whole duration of ground motions, and the distribution width and shape of the probability density function of the displacements at each moment of time, change significantly compared with those in the uncontrolled cases.
-
Key words:
- earthquake ground motion /
- randomness /
- viscous damper /
- shaking table test /
- seismic mitigation
-
图 1 两条典型地震动加速度时程及傅里叶幅值谱
Figure 1. Two typical histories of ground accelarations and their Fourier amplitude spectra
图 2 均值参数地震动加速度时程及傅里叶幅值谱（W000）
Figure 2. Time history of mean-valued ground motion and its Fourier amplitude spectrum (W000)
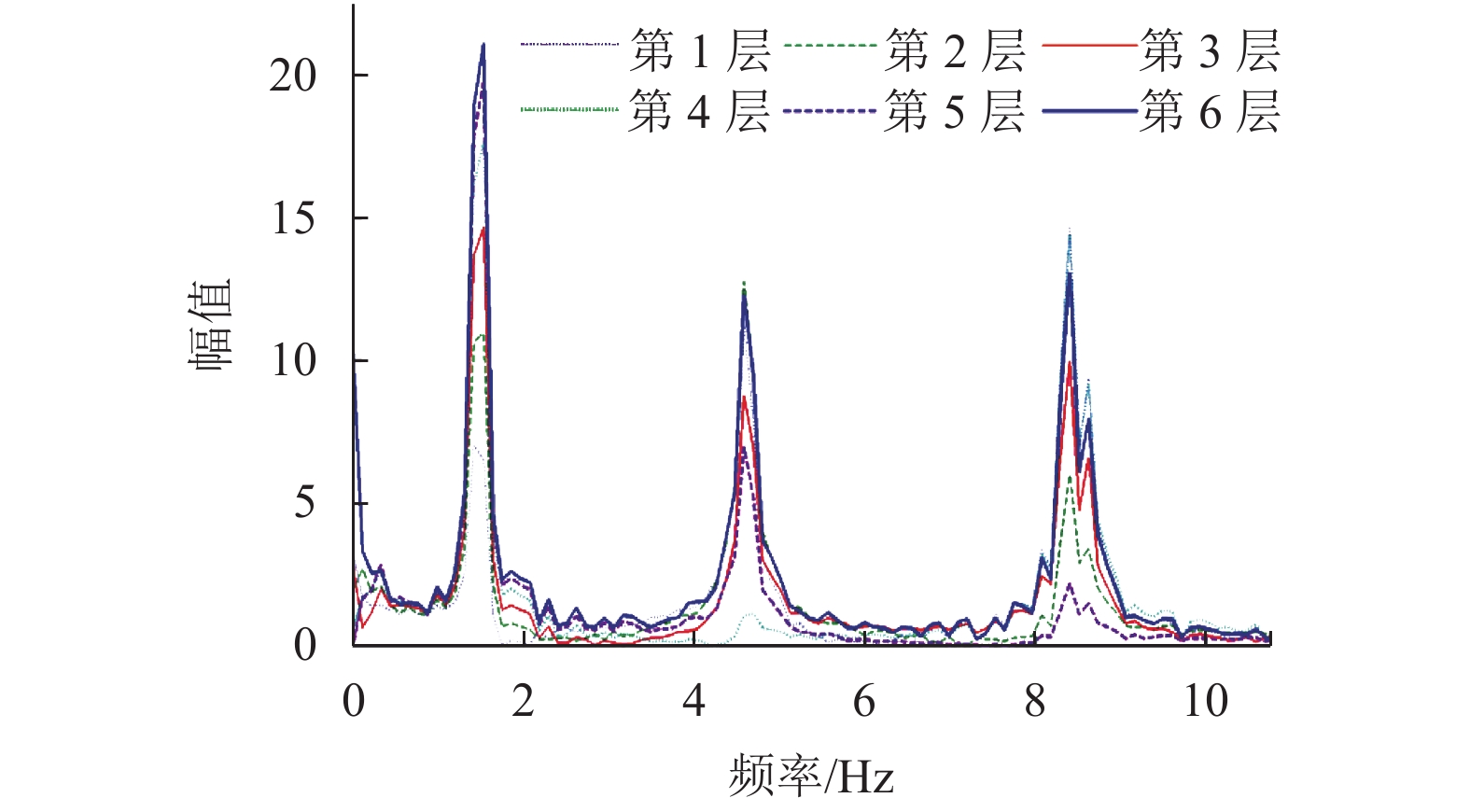
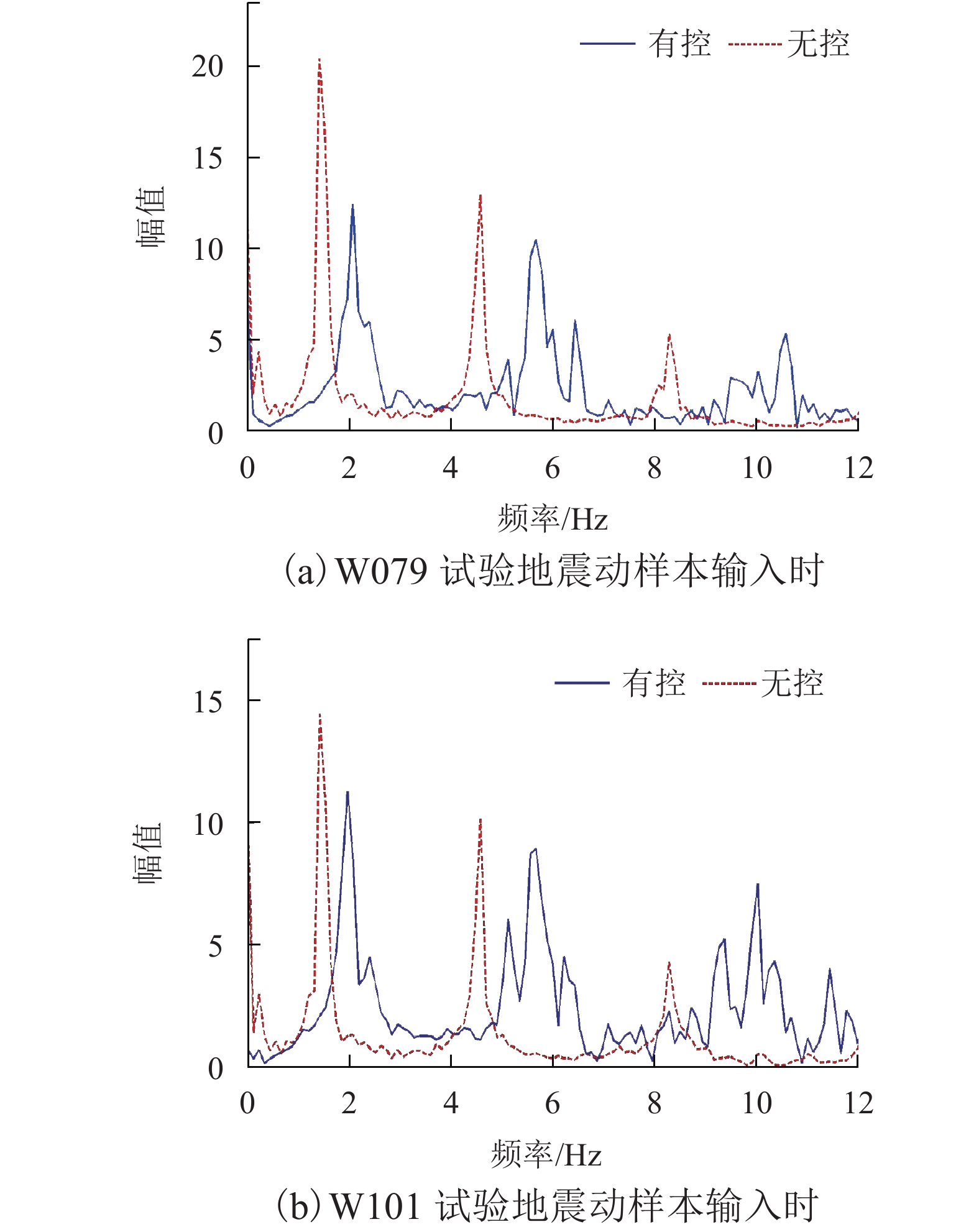
图 6 各楼层绝对加速度响应幅频特性曲线（工况1）
Figure 6. Amplitude-frequency curves of absolute acceleration responses of each story (Case 1 in Table 2)
图 9 有控及无控时试验模型峰值响应
Figure 9. Peak responses of test structure with and without control
图 10 有控及无控时试验模型均方根响应
Figure 10. RMS responses of test structure with and without control
图 11 W079输入时试验模型典型动力响应对比
Figure 11. Comparison of typical responses of test structure subject to ground acceleration W079
图 12 W101输入时试验模型典型动力响应对比
Figure 12. Comparison of typical responses of test structure subject to ground acceleration W101
图 13 顶层绝对加速度响应幅频特性曲线
Figure 13. Amplitude-frequency curves of absolute acceleration of the top floor
图 14 典型峰值响应减振率的概率分布
Figure 14. Probability distributions of vibration-reduction ratios of typical peak responses
图 15 典型均方根响应减振率的概率分布
Figure 15. Probability distributions of vibration-reduction ratios of typical RMS responses
图 16 典型动力响应均值及标准差时程对比
Figure 16. Comparison of time histories of mean and standard deviation of typical responses
图 17 底层位移在典型时段的概率密度演化曲面（3.4~3.8 s）
Figure 17. PDF surfaces of interstory drifts of the first floor in the interval 3.4~3.8 s
图 18 底层位移在两个典型时刻的概率密度函数
Figure 18. PDFs of interstory drift of the first floor at two typical instants of time
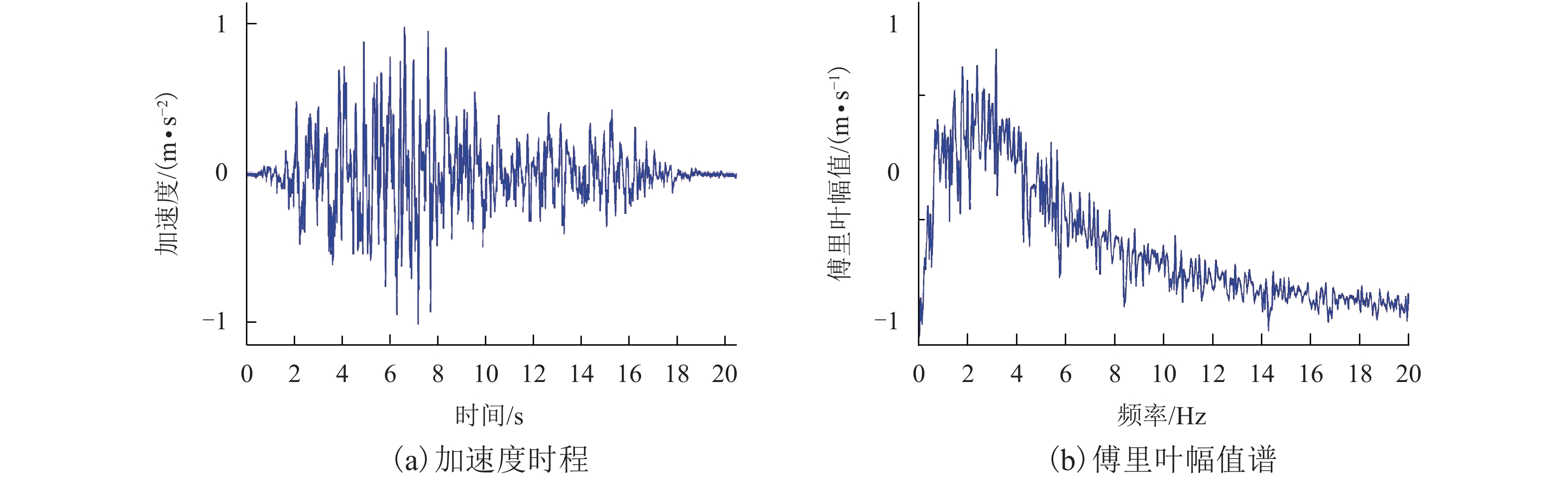
表 1 随机地震动模型的相关参数
Table 1. Parameters of the stochastic ground motion model
对象 基底幅值 场地基本频率 场地等价
阻尼比初始
相角均值 0.25 m•s–1/2 20.0 rad•s–1 0.7 π 变异系数 0.0 0.4 0.3 1.2 
下载: 导出CSV
表 2 振动台试验工况
Table 2. Experimental program of shaking table test
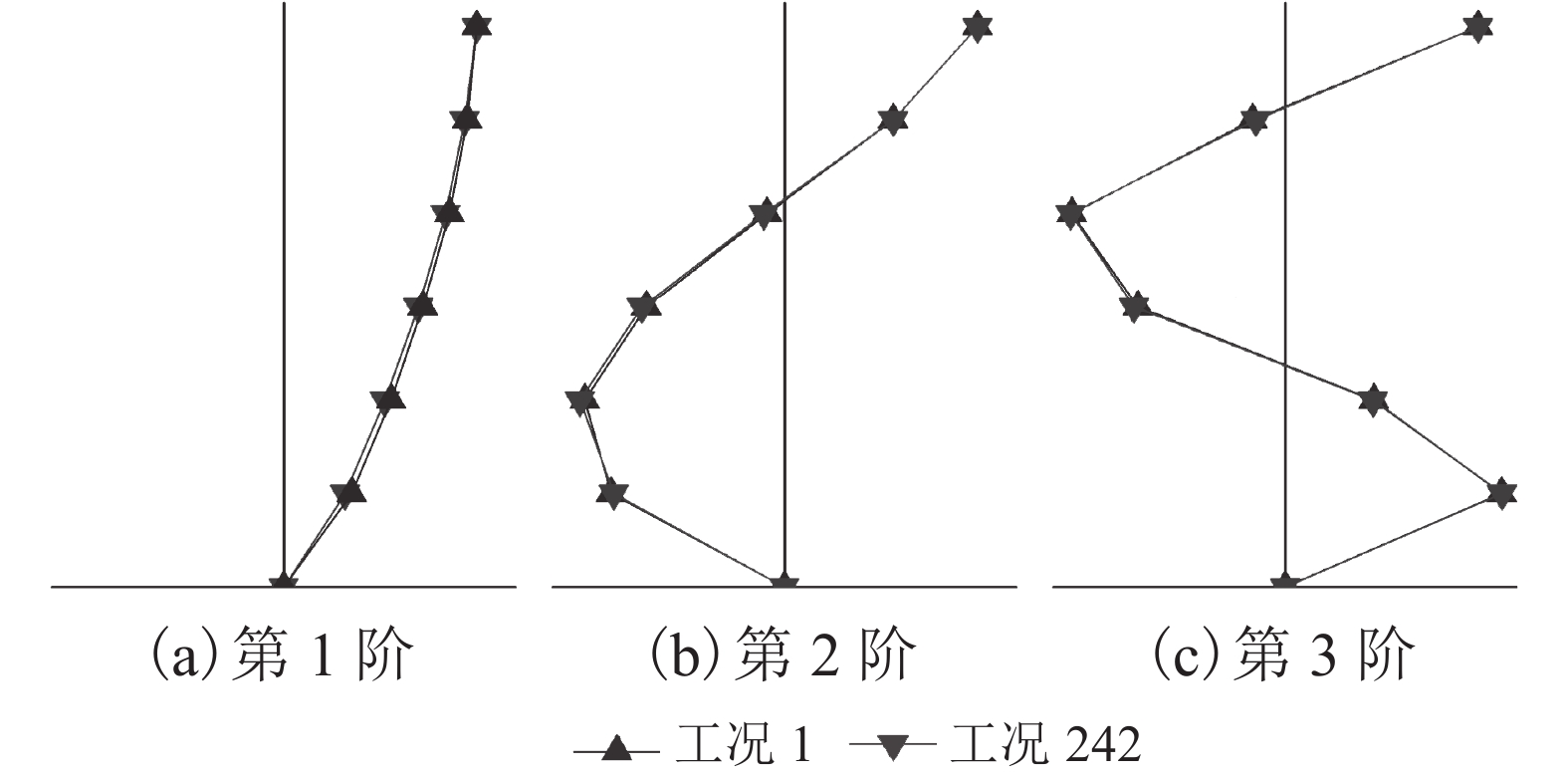
工况 地震动输入 地震动加速度峰值/(m•s–2) 备注 1 W000 1.00 无控 2~121 W001~W120 最小值0.39；最大值2.30；
均值1.09；标准差0.31有控 122~241 W001~W120 最小值0.39；最大值2.30；
均值1.09；标准差0.31无控 242 W000 1.00 无控
下载: 导出CSV
表 3 典型动力响应减振率的均值和标准差
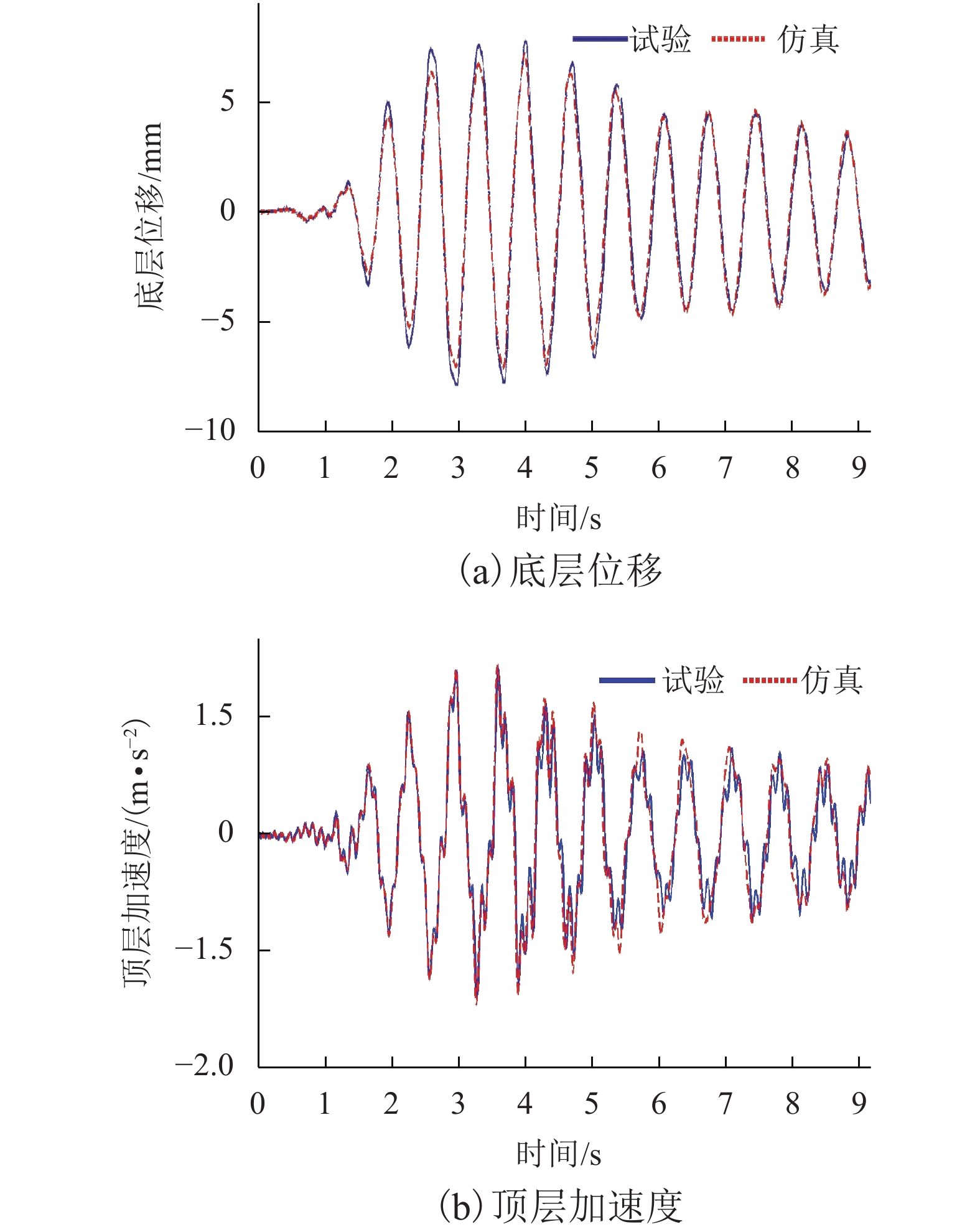
Table 3. Means and standard deviations of vibration-reduction ratios of typical responses
典型动力响应 减振率 均值 标准差 底层位移峰值 0.731 0.045 顶层绝对加速度峰值 – 0.382 0.245 底层位移均方根值 0.801 0.032 顶层绝对加速度均方根值 – 0.071 0.141
下载: 导出CSV
-
陈永祁,曹铁柱,马良喆. 液体黏滞阻尼器在超高层结构上的抗震抗风效果和经济分析[J]. 土木工程学报,2012,45(3): 58-66CHEN Yongqi, CAO Tiezhu, MA Liangzhe. The function and economic effectiveness of fluid viscous dampers for reduction of seismic and wind vibrations of high-rise buildings[J]. China Civil Engineering Journal, 2012, 45(3): 58-66 丁幼亮,耿方方,葛文浩,等. 多塔斜拉桥风致抖振响应的粘滞阻尼器控制研究[J]. 工程力学,2015,32(4): 130-137DING Youliang, GENG Fangfang, GE Wenhao, et al. Control of wind-induced buffeting responses of a multi-tower cable-stayed bridge using viscous dampers[J]. Engineering Mechanics, 2015, 32(4): 130-137 GUO T, LIU J, PAN S. Displacement monitoring of expansion joints of long-span steel bridges with viscous dampers[J]. Journal of Bridge Engineering, 2014, 20(9): 430-437 张微敬,钱稼茹,沈顺高,等. 北京A380机库采用粘滞阻尼器的减振控制分析[J]. 建筑结构学报,2009,30(2): 1-7ZHANG Weijing, QIAN Jiaru, SHEN Shungao, et al. Vibration reduction analyses of Beijing A380 hangar structure with viscous dampers[J]. Journal of Building Structures, 2009, 30(2): 1-7 GRECO R, AVAKIAN J, MARANO G C. A comparative study on parameter identification of fluid viscous dampers with different models[J]. Archive of Applied Mechanics, 2014, 84(8): 1117-1134 赵国辉,刘健新,李宇. 基于随机振动的液体黏滞阻尼器参数优化[J]. 西南交通大学学报,2013,48(6): 1002-1007ZHAO Guohui, LIU Jianxin, LI Yu. Parameter optimization of fluid viscous damper based on stochastic vibration[J]. Journal of Southwest Jiaotong University, 2013, 48(6): 1002-1007 赵卫华,王平,曹洋. 大跨度钢桁斜拉桥上无缝线路制动力的计算[J]. 西南交通大学学报,2012,47(3): 361-366ZHAO Weihua, WANG Ping, CAO Yang. Calculation of braking force of continuous welded rail on large-span steel truss cable-stayed bridge[J]. Journal of Southwest Jiaotong University, 2012, 47(3): 361-366 CONSTANTINOU M C, SYMANS M D. Experimental and analytical investigation of seismic response of structures with supplemental fluid viscous dampers: NCEER-92-0032[R]. Buffalo: State University of New York at Buffalo, 1992 REINHORN A M, LI C, CONSTANTINOU M C. Experimental and analytical investigation of seismic retrofit of structures with supplemental damping: part 1- fluid viscous damping devices: NCEER-95-0001[R]. Buffalo: State University of New York, 1995 范峰,沈世钊. 网壳结构的粘滞阻尼减振分析与试验研究[J]. 地震工程与工程振动,2000,20(1): 105-111FAN Feng, SHEN Shizhao. Vibration reducing analysis and experimental study of viscous damper on reticulated shells[J]. Earthquake Engineering and Engineering Vibration, 2000, 20(1): 105-111 吕西林,孟春光,田野. 消能减震高层方钢管混凝土框架结构振动台试验研究和弹塑性时程分析[J]. 地震工程与工程振动,2006,26(4): 231-238Lü Xilin, MENG Chunguang, TIAN Ye. Shaking table test and elasto-plastic time history analysis of a high-rise CFRT frame structure with dampers[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(4): 231-238 WANG D, LI J. Physical random function model of ground motions for engineering purposes[J]. Science China Technological Sciences, 2011, 54(1): 175-182 李杰,艾晓秋. 基于物理的随机地震动模型研究[J]. 地震工程与工程振动,2006,26(5): 21-26LI Jie, AI Xiaoqiu. Study on random model of earthquake ground motion based on physical process[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(5): 21-26 艾晓秋,李杰. 基于随机Fourier谱的地震动合成研究[J]. 地震工程与工程振动,2009,29(2): 7-12AI Xiaoqiu, LI Jie. Synthesis method of non-stationary ground motion based on random Fourier spectra[J]. Earthquake Engineering and Engineering Vibration, 2009, 29(2): 7-12 梅真,陈建兵,李杰. 随机地震动作用下的结构振动控制试验设计[J]. 世界地震工程,2012,28(1): 157-163MEI Zhen, CHEN Jianbing, LI Jie. Experimental design of structural vibration control subject to random earthquake ground motions[J]. World Earthquake Engineering, 2012, 28(1): 157-163 李国强, 李杰. 工程结构动力检测理论与应用[M]. 北京:科学出版社, 2002: 17-33 BOWMAN A W, AZZALINI A. Applied smoothing techniques for data analysis[M]. Oxford: Oxford University Press, 1997: 1-6 LI J, CHEN J B. Stochastic dynamics of structures[M]. Singapore: John Wiley & Sons, 2009: 215-222 -
下载:
点击查看大图
计量
- 文章访问数: 436
- HTML全文浏览量: 171
- PDF下载量: 39
- 被引次数: 0