层状软岩隧道围岩破坏的连续-离散耦合分析

徐国文; 何川; 汪耀; 陈子全

doi:10.3969/j.issn.0258-2724.2018.05.013

层状软岩隧道围岩破坏的连续-离散耦合分析

doi: 10.3969/j.issn.0258-2724.2018.05.013

徐国文^1,,
何川^1, ,,
汪耀²,
陈子全¹

详细信息

作者简介:
徐国文(1988—)，男，博士，研究方向为隧道与地下工程，E-mail： xgw80033@163.com

通讯作者:
何川(1964—) ，男，教授，博士，博士生导师，研究方向为隧道与地下工程，E-mail:chuanhe21@163.com

中图分类号: O319.56
计量
- 文章访问数: 463
- HTML全文浏览量: 223
- PDF下载量: 55
- 被引次数: 0
出版历程
- 收稿日期: 2016-04-17
- 刊出日期: 2018-10-01

Failure Analysis on Surrounding Rock of Soft-Layered Rock Tunnel Using Coupled Continuum-Discrete Model

XU Guowen^1
,,
HE Chuan^{1
, ,},
WANG Yao²,
CHEN Ziquan¹

摘要

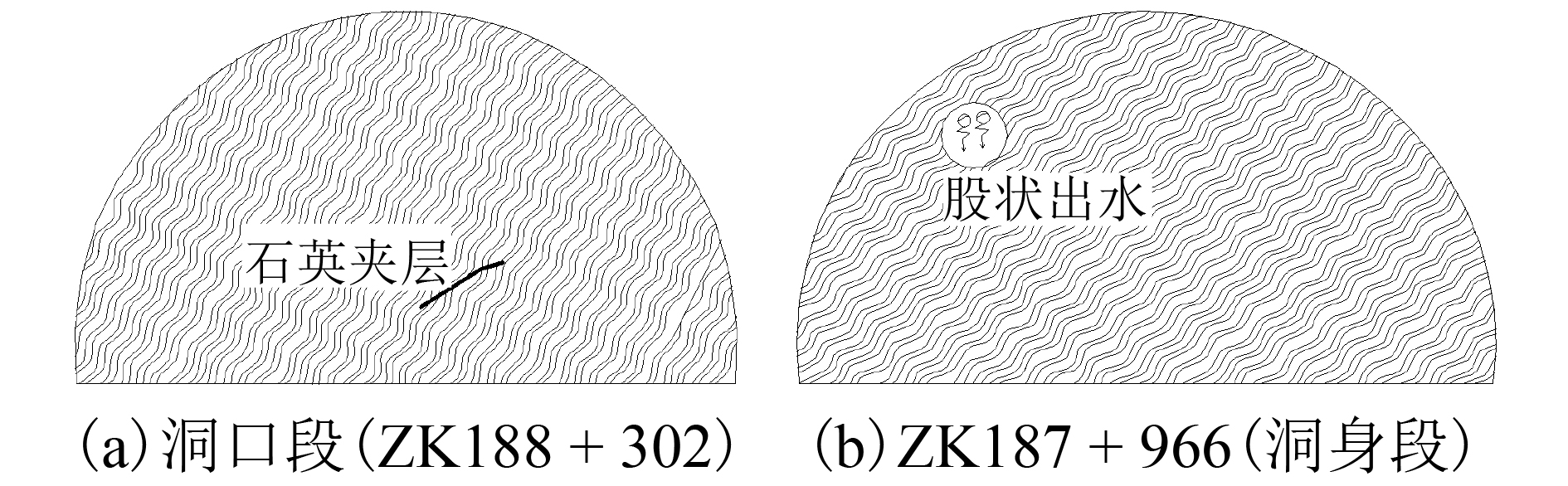
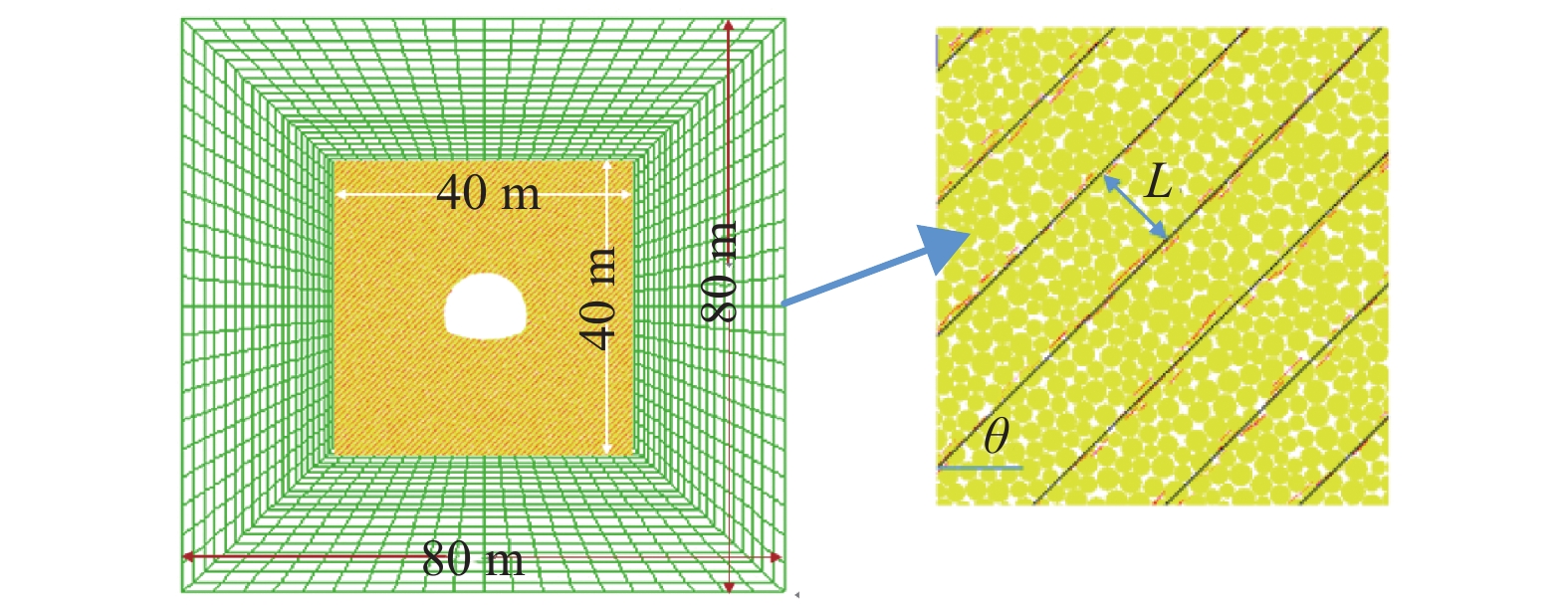
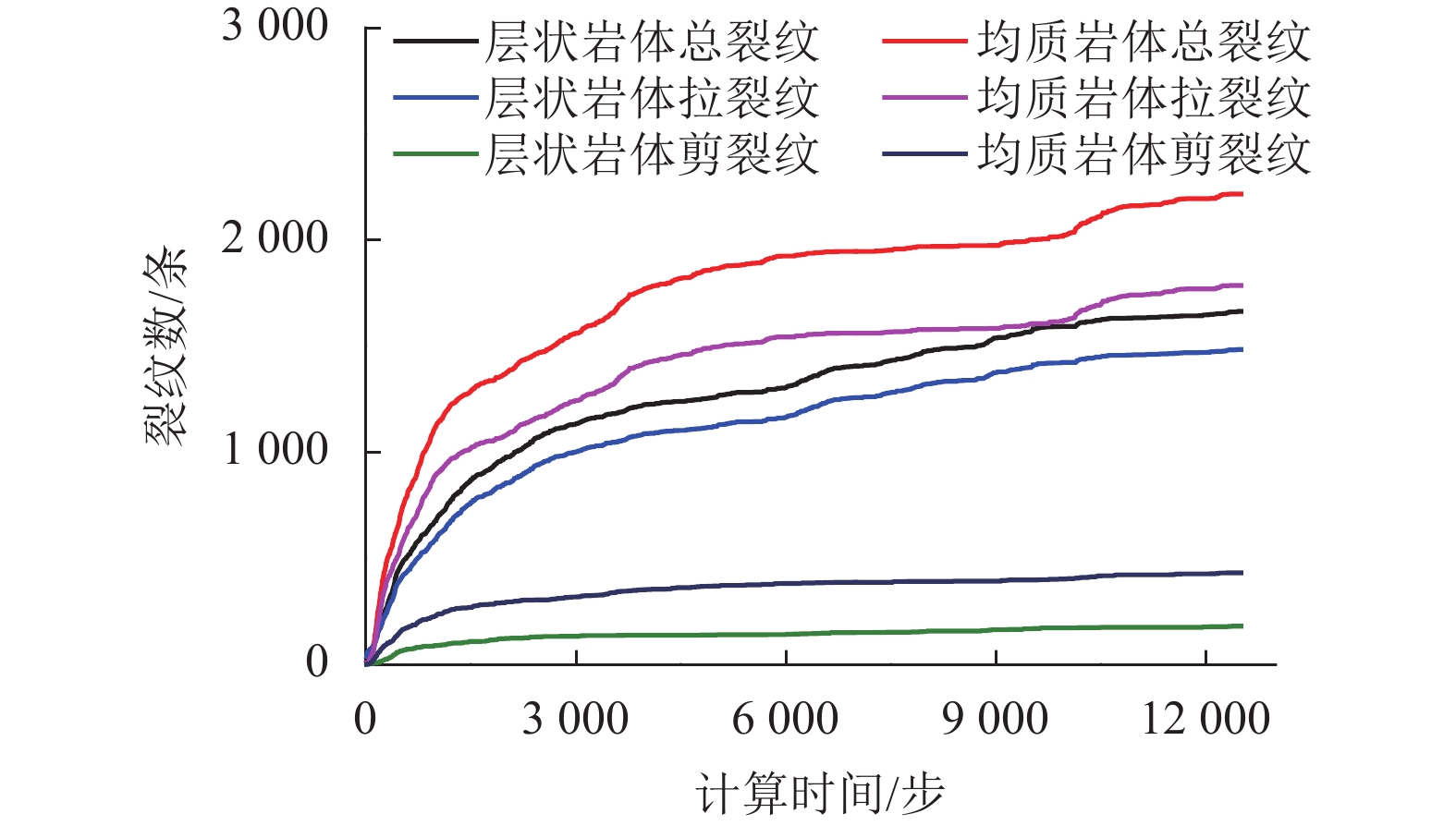
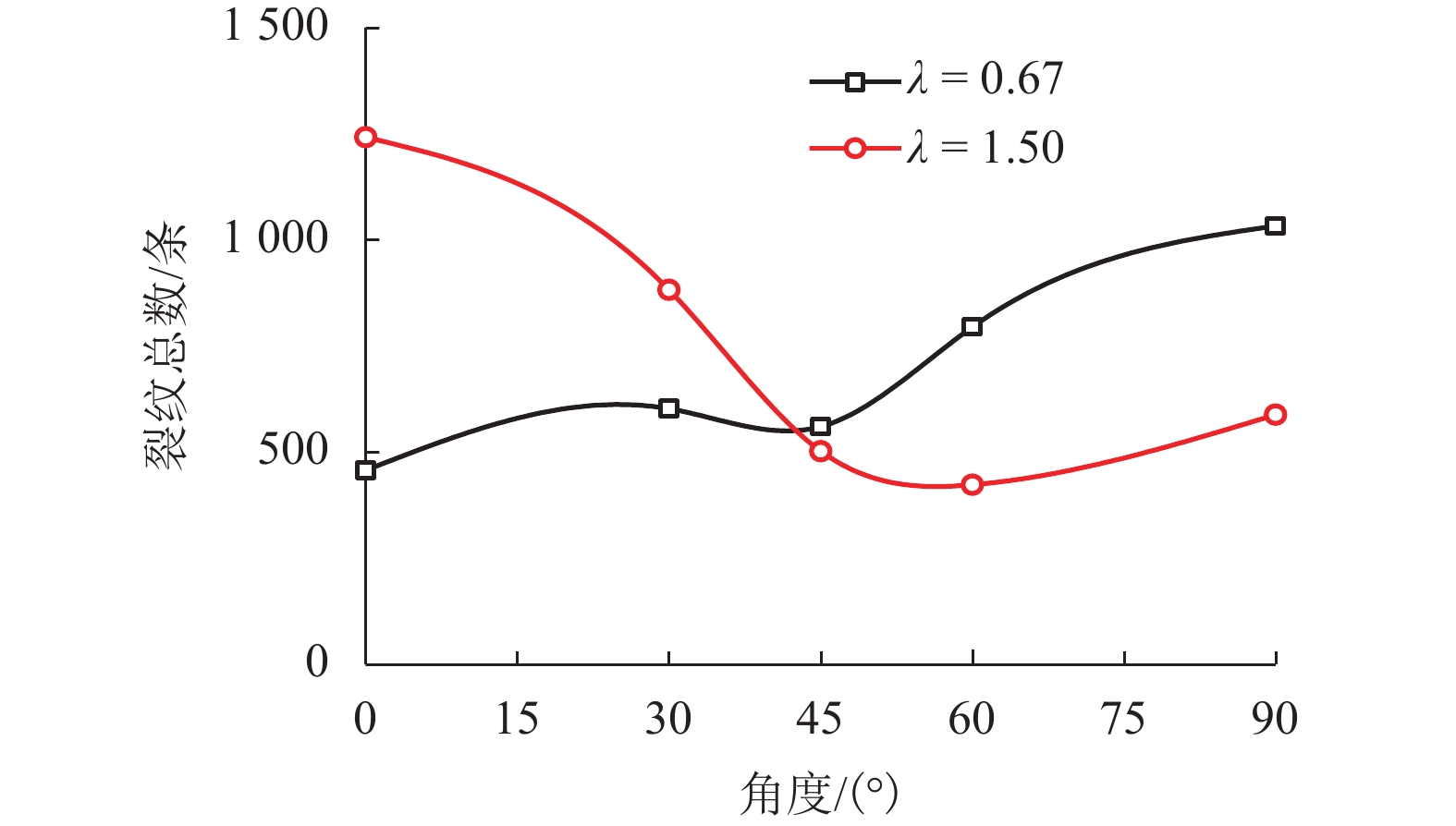
摘要: 为了研究层状岩体中隧道开挖后围岩的破坏机理，以汶马高速鹧鸪山隧道为例，基于离散元-有限差分耦合算法，建立了一种新的层状软岩隧道开挖模拟方法，采用该方法对不同地应力场、层理间距等因素影响下围岩的破坏模式进行了数值模拟. 研究结果表明：隧道开挖后，应力重分布导致强度较低的层理面首先发生滑移及张开破坏，岩体的滑移及张开使得应力场受到进一步扰动，导致层间岩体产生拉裂破坏；同种水平应力条件下，随着侧压力系数的减小，岩体产生的微裂纹不断增多. 当侧压力系数为1.00、0.80、0.67、0.57、0.50时，微裂纹总数分别为304、391、602、999、1 240；当层理间距为0.6 m时，层理对围岩破坏形态起控制作用；随着层理间距从0.6 m增加至1.2 m，层理对围岩破坏模式的控制作用减弱，围岩的破坏形态与均质围岩相似.
- 层状岩体 /
- 软岩 /
- 破坏特征 /
- 连续-离散耦合分析
Abstract: In order to study the failure mechanism of layered surrounding rock after tunnel excavation, taking the Zhegu mountain tunnel of Wenma highway as an example, a new numerical approach is put forward based on continuum-discrete coupling method. The failure patterns of surrounding rock under different geo-stress fields and bedding spacing are obtained through this method. The results show that: slipping and opening failure occurs on joint surface because of its low strength after stress redistribution during tunnel excavation. Then, stress field is disturbed furtherly and this disturbance leads to tensile failure of rock matrix; Micro-cracks in rock mass increases with the decrease of lateral pressure coefficient for the same stress level. When the lateral pressure coefficient is 1.00, 0.80, 0.67, 0.57, and 0.50, the total number of micro-cracks is 304, 391, 602, 999, and 1240, respectively. When the bedding spacing is 0.6 m, bedding has a controlling influence on the failure mode of surrounding rock, while this influence is weakened and the failure mode is similar to that of homogeneous surrounding rock with the increase of bedding spacing from 0.6 m to 1.2 m.
- layered rock mass /
- soft rock /
- failure mechanics /
- coupled continuum-discrete analysis

HTML全文

图 1 鹧鸪山隧道隧址区区域构造图

Figure 1. Regional tectonic map of Zhegu mountain tunnel

下载: 全尺寸图片幻灯片

图 2 大变形现象

Figure 2. Large deformation

下载: 全尺寸图片幻灯片

图 3 典型掌子面地质素描图

Figure 3. Typical geological sketch map of tunnel face

下载: 全尺寸图片幻灯片

图 4 数值模拟与试验结果对比

Figure 4. Comparison between numerical simulation and experimental results

下载: 全尺寸图片幻灯片

图 5 耦合示意图

Figure 5. Coupling method

下载: 全尺寸图片幻灯片

图 6 计算模型

Figure 6. Numerical model

下载: 全尺寸图片幻灯片

图 7 围岩破坏过程

Figure 7. Failure process of surrounding rock

下载: 全尺寸图片幻灯片

图 8 破裂增长曲线

Figure 8. Fracture growth curve

下载: 全尺寸图片幻灯片

图 9 层理方向对破裂影响

Figure 9. Effect of bedding direction to rupture

下载: 全尺寸图片幻灯片

图 10 裂纹总数与角度关系

Figure 10. Relationship between total number of cracks and angle

下载: 全尺寸图片幻灯片

图 11 应力场对破裂的影响

Figure 11. Effect of stress field to fracture

下载: 全尺寸图片幻灯片

图 12 层理间距对破裂的影响

Figure 12. Effect of bedding spacing on rupture

下载: 全尺寸图片幻灯片

表 1 BPM模型参数

Table 1. Parameters of BPM

参数	数值	参数	数值
颗粒最小半径/mm	0.18	平行黏结系数	1
最大最小颗粒半径比	1.66	平行黏结弹性模量/GPa	36
颗粒密度/（kg•m^–3）	2 730	平行黏结法向-切向刚度比	3.3
颗粒间摩擦因数	0.5	平行黏结法向强度/MPa	65 ± 15
颗粒法向-切向刚度比	3.3	颗粒弹性体模量 /GPa	38
		平行黏结法向强度/MPa	120 ± 30

下载: 导出CSV

表 2 SMJ模型参数

Table 2. Parameters of SMJ

参数	数值	参数	数值
法向刚度 /（GPa•m^–1）	3 700	黏结模式	切向与法向黏结
切向刚度 /（GPa•m^–1）	860	黏结法向强度/MPa	3.5
摩擦因数	0.4	黏结黏聚力/MPa	20
剪胀角/（°）	0	黏结摩擦角/（°）	14

下载: 导出CSV

表 3 连续单元计算参数

Table 3. Parameters of FDM

密度ρ/（kg•m^–3）	弹性模量E/GPa	泊松比ν
2 600	20	0.23

下载: 导出CSV

表 4 平行粘结模型参数

Table 4. Parameters of parallel bond

颗粒最小半径/cm	最大最小颗粒半径比	颗粒密度/ （kg•m^–3）	颗粒间摩擦因数	颗粒弹性体模量/ GPa	颗粒法向- 切向刚度比	平行黏结系数	平行黏结弹性模量/ GPa	平行黏结法向-切向刚度比	平行黏结法向强度/ MPa	平行黏结法向强度/ MPa
6	1.66	2 600	0.5	20	2.5	1	20	2.5	12 ± 2	12 ± 2

下载: 导出CSV

表 5 光滑节理模型参数

Table 5. Parameters of smooth joint

法向刚度/（N•m^–1）	切向刚度/（N•m^–1）	摩擦因数	剪胀角/（°）	黏结模式	黏结法向强度/MPa	黏结黏聚力/MPa	黏结摩擦角/（°）
2 × 10¹³	2 × 10¹³	0.5	0	3	2	2	15

下载: 导出CSV

表 6 裂纹统计表

Table 6. Crack number

侧压力系数	裂纹总数/条	拉裂纹占比/%	剪裂纹占比/%
1.00	304	94.1	5.9
0.80	391	92.8	7.2
0.67	602	91.6	7.0
0.57	999	91.3	8.7
0.50	1 240	89.9	10.1

下载: 导出CSV

参考文献(16)

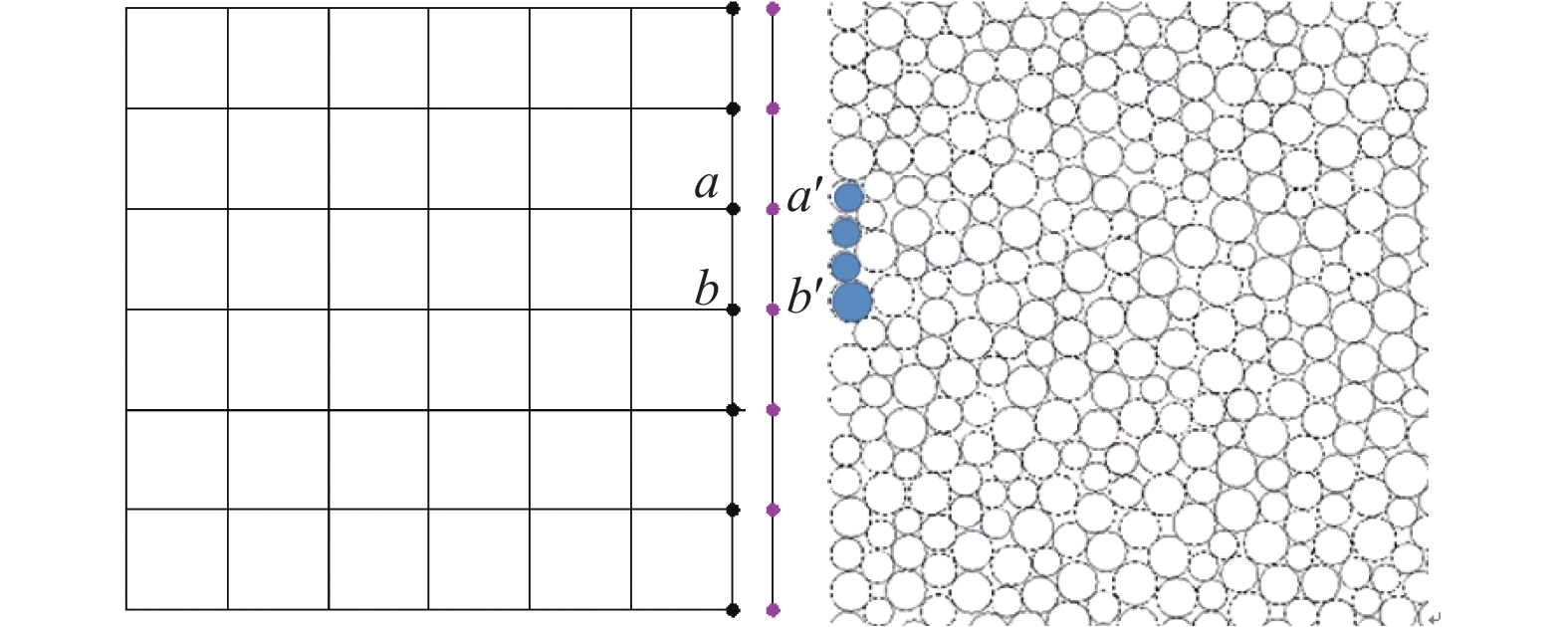
韩昌瑞,张波,白世伟,等. 深埋隧道层状岩体弹塑性本构模型研究[J]. 岩土力学,2008,29(9): 2404-2408

HAN Changrui, ZHANG Bo, BAI Shiwei, et al. Research on elastoplastic constitutive model of layered surrounding rock mass of a deep buried tunnel[J]. Rock and Soil Mechanics, 2008, 29(9): 2404-2408

TIEN Y M, KUO M C, JUANG C. An experimental investigation of the failure mechanism of simulated transversely isotropic rocks[J]. International Journal of Rock Mechanics and Mining Science, 2006, 43(8): 1163-1181

LISJAK A, GARITTE B, GRASSELLI G, et al. The excavation of a circular tunnel in a bedded argillaceous rock (opalinus clay): short-term rock mass response and FDEM numerical analysis[J]. Tunnelling and Underground Space Technology, 2015, 45: 227-248

BLUMLING P, BERNIER F, LEBON P, et al. The excavation damaged zone in clay formations time-dependent behaviour and influence on performance assessment[J]. Phys. Chem. Earth Parts A/B/C, 2007, 32: 588-599

沙鹏,伍法权,李响,等. 高地应力条件下层状地层隧道围岩挤压变形与支护受力特征[J]. 岩土力学,2015,36(5): 1407-1414

SA Peng, WU Faquan, LI Xiang, et al. Squeezing deformation in layered surrounding rock and force characteristics of support system of a tunnel under high in-situ stress[J]. Rock and Soil Mechanics, 2015, 36(5): 1407-1414

夏彬伟. 深埋隧道层状岩体破坏失稳机理实验研究[D]. 重庆: 重庆大学, 2009

周晓军,高杨,李泽龙,等. 地质顺层偏压隧道围岩压力及其分布特点的试验研究[J]. 现代隧道技术,2006,43(1): 12-21

ZHOU Xiaojun, GAO Yang, LI Zelong, et al. Experimental study on the uneven rock pressure and its distribution applied on a tunnel embedded in geologically bedding strata[J]. Modern Tunnelling Technology, 2006, 43(1): 12-21

LABIOUSE V, VIECTOR T. Laboratory and in-situ simulation tests of the excavation damaged zone around galleries in Opalinus Clay[J]. Rock Mechanics and Rock Engineering, 2014, 47: 57-70

CORKUM A G. Behaviour of Opalinus Clay around deep underground excavations[D]. Edmonton: University of Alberta, 2006

POPP T, SALZER K, MINKLEY W. Influence of bedding planes to EDZ-evolution and the coupled HM properties of opalinus clay. phys. chem[J]. Earth, 2008, 33: 374-387

YOUNG S, KAISER P K, LOEW S. Influence of tectonic shears on tunnel-induced fracturing[J]. International journal of rock mechanics and mining science, 2010, 47: 894-907

JUNG-WOO C, HANNA K, SEOKWON J, et al. Deformation and strength anisotropy of Asan gneiss, Boryeong shale, and Yeoncheon schist[J]. International journal of Rock Mechanics and Mining Science, 2012, 50: 158-169

ZHOU Jian, JIAN Qiwei, ZHANG Jiao, et al. Coupled 3D discrete-continuum numerical modeling of pile penetration in sand[J]. Journal of Zhejiang University-Science A: Applied Physics & Engineering, 2012, 13(1): 44-55

孙新坡,何思明,刘恩龙,等. 基于离散元和有限差分耦合算法的崩塌体和结构碰撞预测分析[J]. 工程力学,2014,31(12): 32-39

SUN Xinpo, HE Siming, LIU Enlong, et al. Prediction analysis for impact of collapse bodies on structures based on unified discrete element and finite difference numerical simulation[J]. Engineering mechanics, 2014, 31(12): 32-39

李永兵,周喻,吴顺川,等. 圆形巷道围岩变形破坏的连续–离散耦合分析[J]. 岩石力学与工程学报,2015,34(9): 1849-1858

LI Yongbing, ZHOU Yu, WU Shunchuan, et al. Deformation and failure analysis on surrounding rock of circular tunnel using coupled continuum-discrete method[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(9): 1849-1858

严琼,吴顺川,周喻,等. 基于连续-离散耦合的边坡稳定性分析研究[J]. 岩土力学,2015,36(增刊2): 47-56

YAN Qiong, WU Shunchuan, ZHOU Yu, et al. Slope stability analysis based on technology of continuum-discrete coupling[J]. Rock and Soil Mechanics, 2015, 36(Sup.2): 47-56

施引文献

附加材料(0)

访问统计