Analysis of Guided Wave Behaviour in Rails Using Numerical or Analytical Models
-
摘要: 钢轨振动由沿钢轨传递的各类导波构成，是铁路滚动噪声的主要贡献者. 为了研究铁路轨道的动力特性，分别基于铁木辛柯梁理论和波导有限元法建立了两种分析模型，推导自由波响应和受迫响应的求解过程，以波数、群速度、速度导纳和衰减率为指标，分析了两种模型条件下钢轨的波导特性. 研究结果表明：波导有限元模型包含了钢轨横截面所有的变形特征，可表征6 kHz内钢轨中的8种导波及其特性，反映导波波型交换、群速度互换的现象，以及高阶导波激发引起的导纳峰值；铁木辛柯梁模型可识别包括弯曲波、扭转波和纵波在内的5种钢轨导波，无法揭示截止频率在1.5 kHz以上与钢轨截面变形相关的导波；铁木辛柯梁模型可给出2 kHz内合理的钢轨垂向原点速度导纳计算结果.Abstract: The vibration of rails is a major contributor to railway rolling noise, and consists of different guided waves that propagate along the rail. To study the dynamic behaviour of a railway track, models based on the Timoshenko beam theory and the waveguide finite-element method were established. The solution procedures to obtain the free wave response and the forced response for each model were determined. The characteristics of guided waves in rails, such as wavenumber, group velocity, mobility, and decay rate, were analysed based on two different models. The waveguide finite-element model, which includes all the features of rail cross-section deformation, makes it possible to identify eight kinds of guided waves in rails within a frequency range of as much as 6 kHz. Moreover, the phenomena of wave mode exchange and group velocity exchange between waves are discussed, as well as the peak in the mobility caused by the excitation of the higher-order wave mode. The Timoshenko beam model can identify five of these wave modes, including those for bending, torsion, and extensional waves, but it cannot identify the ones associated with cross-section deformations that cut on at frequencies of more than 1.5 kHz. The Timoshenko beam model provides acceptable results for point mobilities of as much as 2 kHz.
-
Key words:
- waveguide finite element /
- Timoshenko beam /
- group velocity /
- mobility /
- railway track
-
图 2 波导有限元模型和铁木辛柯梁模型钢轨导波频散关系对比
Figure 2. Comparison of rail dispersion relation between waveguide finite element model and Timoshenko beam model
图 5 波导有限元模型和铁木辛柯梁模型钢轨导波的群速度对比
Figure 5. Comparison of rail group velocity between waveguide finite-element model and Timoshenko beam model
-
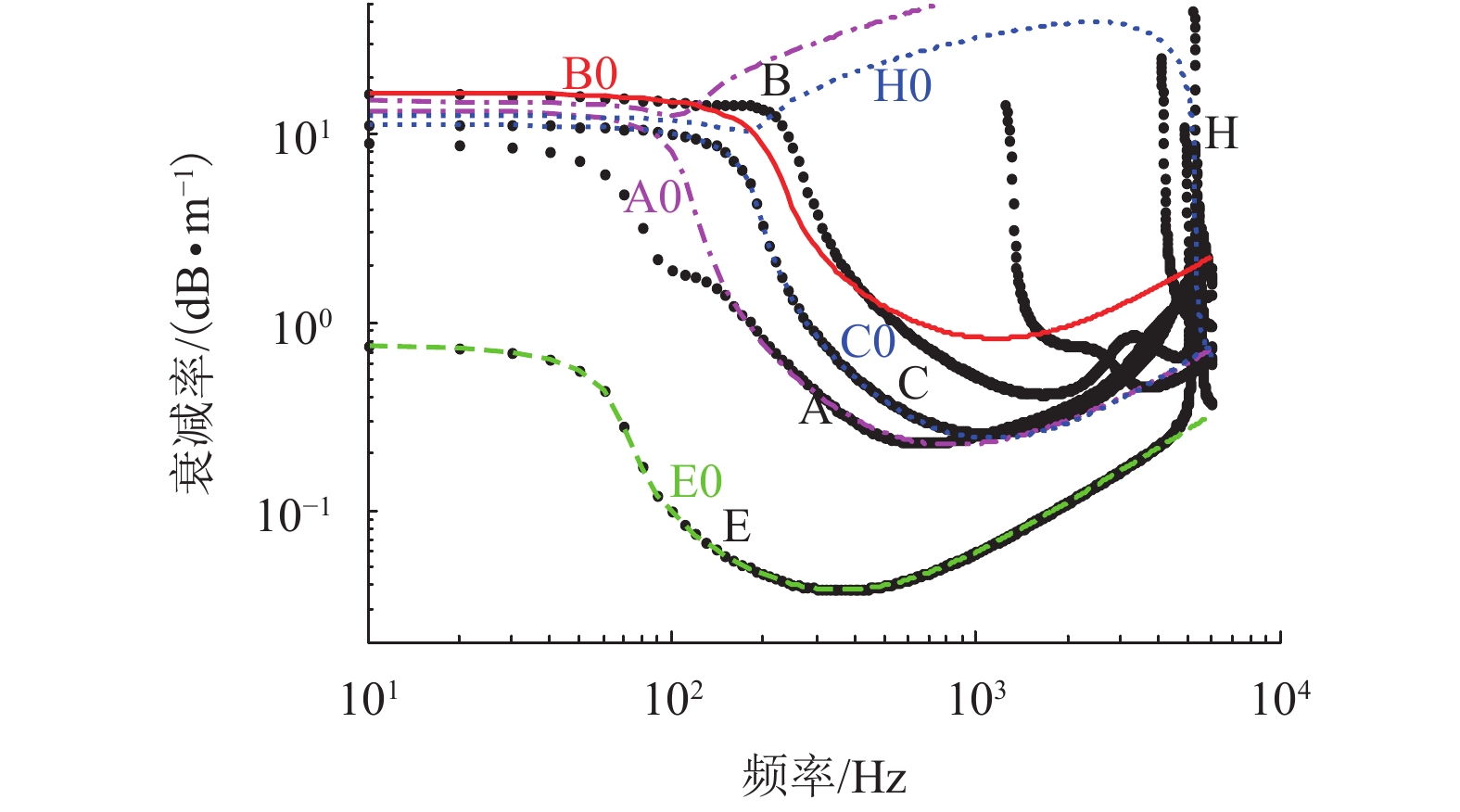
THOMPSON D J. Wheel-rail noise generation,part III:rail vibration[J]. Journal of Sound and Vibration, 1993, 161(3): 421-446 KNOTHE K, GRASSIE S. Modeling of railway track and vehicle/track interaction at high frequencies[J]. Vehicle System Dynamics, 1993, 22(3): 209-262 AALAMI B. Waves in prismatic guides of arbitrary cross-section[J]. Journal of Applied Mechanics, 1973, 40(4): 1067-1072 SNEDDON I N. Fourier transforms[M]. New York: McGraw-Hill, 1951: 28-33 SNEDDON I N. Partial differential equations[M]. New York: McGraw-Hill, 1964: 45-52 NILSSON C M, JONES C J C, THOMPSON D J, et al. A waveguide finite element and boundary element approach to calculating the sound radiated by railway and tram rails[J]. Journal of Sound and Vibration, 2009, 321(3): 813-836 GAVRIC L. Computation of propagative waves in free rail using a finite element technique[J]. Journal of Sound and Vibration, 1995, 185(3): 531-543 RYUE J, THOMPSON D J, WHITE P R, et al. Investigations of propagating wave types in railway tracks at high frequencies[J]. Journal of Sound and Vibration, 2008, 315(1/2): 157-175 RYUE J, THOMPSON D J, WHITE P R. Decay rates of propagating waves in railway tracks at high frequencies[J]. Journal of Sound and Vibration, 2009, 320(4/5): 955-976 卢超,杨雪娟,戴翔,等. 钢轨中导波传播模式的半解析有限元分析与试验测量[J]. 机械工程学报,2015,51(6): 79-86LU Chao, YANG Xuejuan, DAI Xiang, et al. Semi-analytical FEM analysis and experimental measurement for propagating guided waves modes in rail[J]. Journal of Mechanical Engineering, 2015, 51(6): 79-86 许西宁. 基于超声导波的无缝线路钢轨应力在线检测技术应用基础研究[D]. 北京: 北京交通大学, 2013 THOMPSON D J. Railway noise and vibration: mechanisms, modelling and means of control[M]. Oxford: Elsevier, 2009: 59-62 GRAFF K F. Wave motion in elastic solids[M]. Oxford: Oxford University Press, 1975: 75-126 GAVRIC L. Finite element computation of dispersion properties of thin-walled waveguides[J]. Journal of Sound and Vibration, 1994, 173(1): 377-385 DOYLE J F. Wave propagation in structures[M]. New York: Springer, 1997: 27-34 THOMSON W T, DAHLEH M D. Theory of vibration with applications[M]. 5th Edition. Beijing: Tsinghua University Press, 2005: 230-233 马大猷. 噪声与振动控制工程手册[M]. 北京: 机械工业出版社, 2002: 1147-1151 THOMPSON D J, JONES C J C. Review of the modelling of wheel/rail noise generation[J]. Journal of Sound and Vibration, 2000, 231(3): 519-536 -
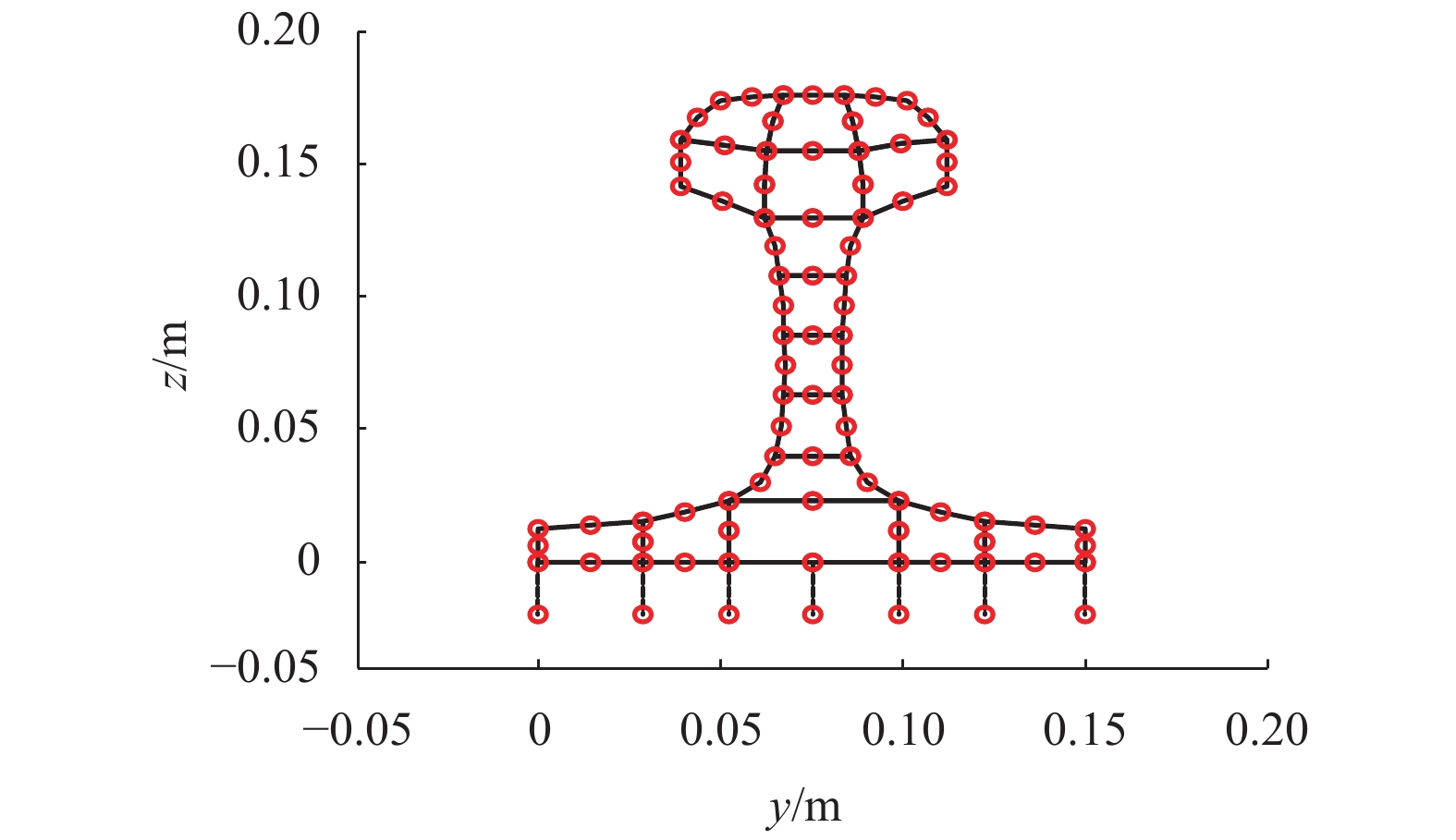
下载:
点击查看大图
图(8)
计量
- 文章访问数: 460
- HTML全文浏览量: 276
- PDF下载量: 94
- 被引次数: 0