温度作用下纵连式无砟轨道垂向稳定性研究

刘笑凯; 刘学毅; 肖杰灵; 邸银桥; 杨荣山

doi:10.3969/j.issn.0258-2724.2018.05.007

温度作用下纵连式无砟轨道垂向稳定性研究

doi: 10.3969/j.issn.0258-2724.2018.05.007

刘笑凯^1,2,,
刘学毅^1,2,
肖杰灵^1,2, ,,
邸银桥^1,2,
杨荣山^1,2

详细信息

作者简介:
刘笑凯（1990—），男，博士研究生，研究方向为轨道结构与轨道力学，E-mail： jlallk@163.com

通讯作者:
肖杰灵（1978—），男，讲师，博士，研究方向为高速、重载轨道结构及轨道动力学，E-mail： xjling@swjtu.cn

中图分类号: U213.213
计量
- 文章访问数: 494
- HTML全文浏览量: 281
- PDF下载量: 62
- 被引次数: 0
出版历程
- 收稿日期: 2017-08-21
- 刊出日期: 2018-10-01

Vertical Stability of Longitudinal Continuous Ballastless Track Under Temperature Variation

LIU Xiaokai^{1,2
,},
LIU Xueyi^1,2,
XIAO Jieling^{1,2
, ,},
DI Yinqiao^1,2,
YANG Rongshan^1,2

摘要

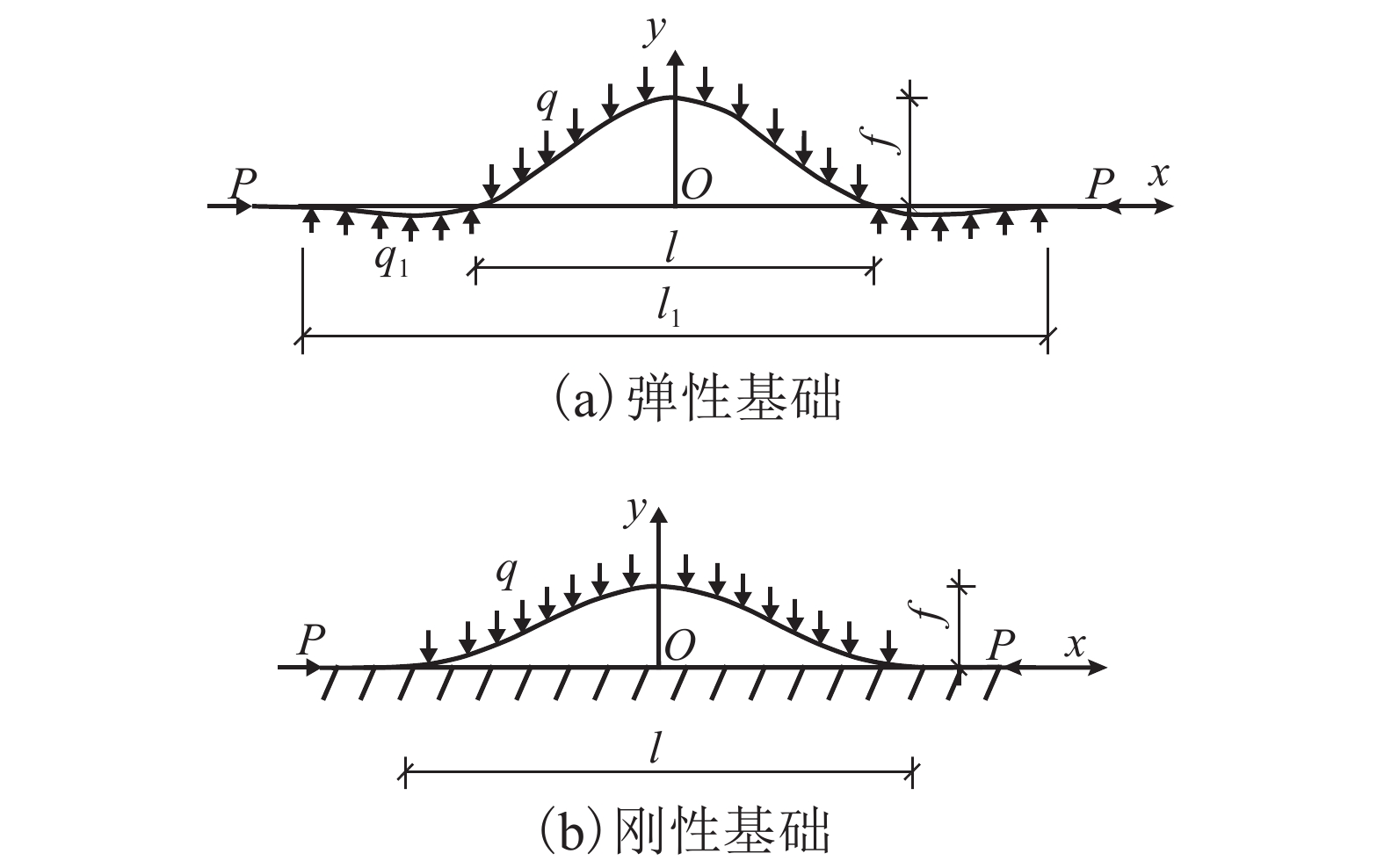
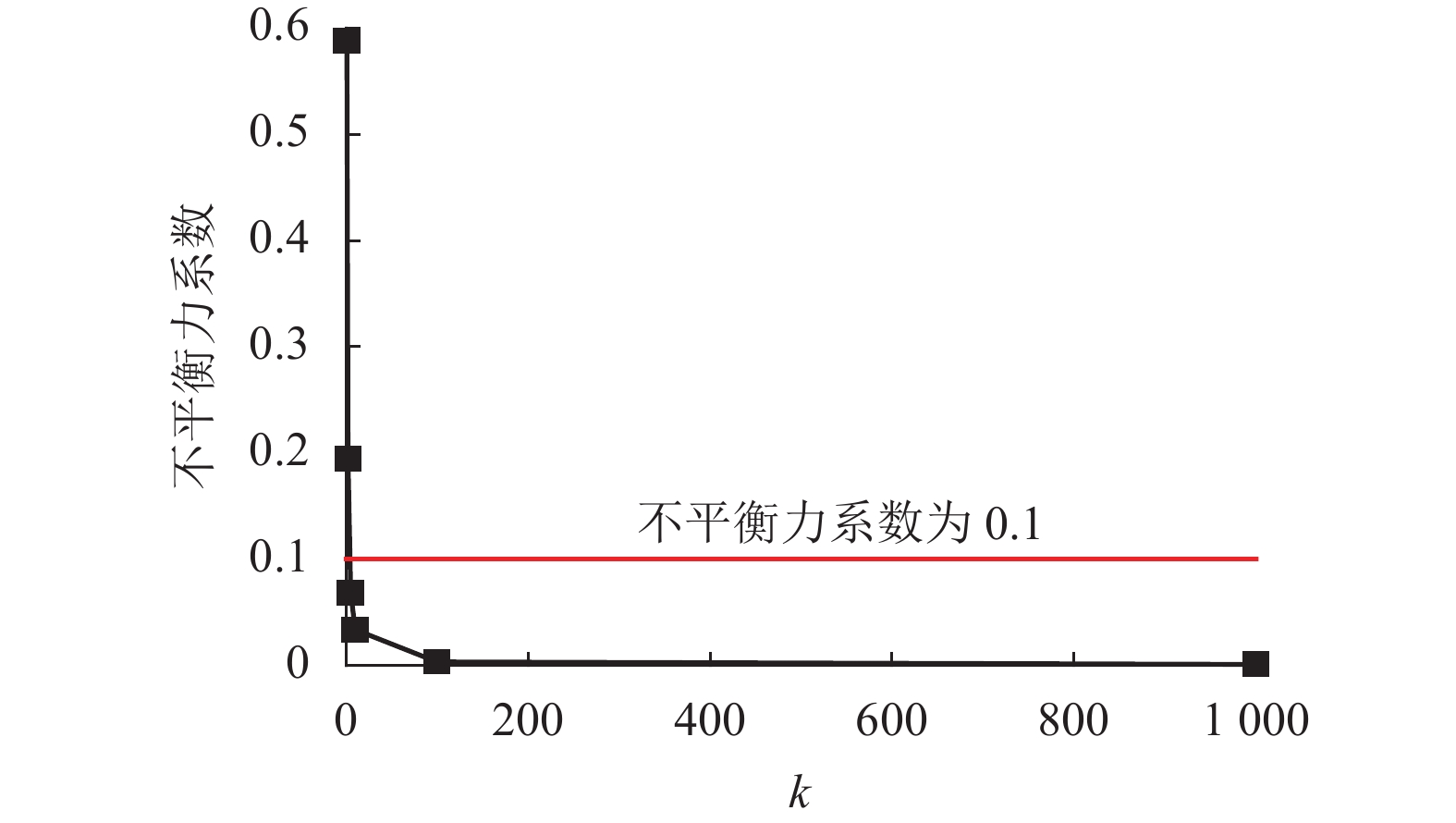
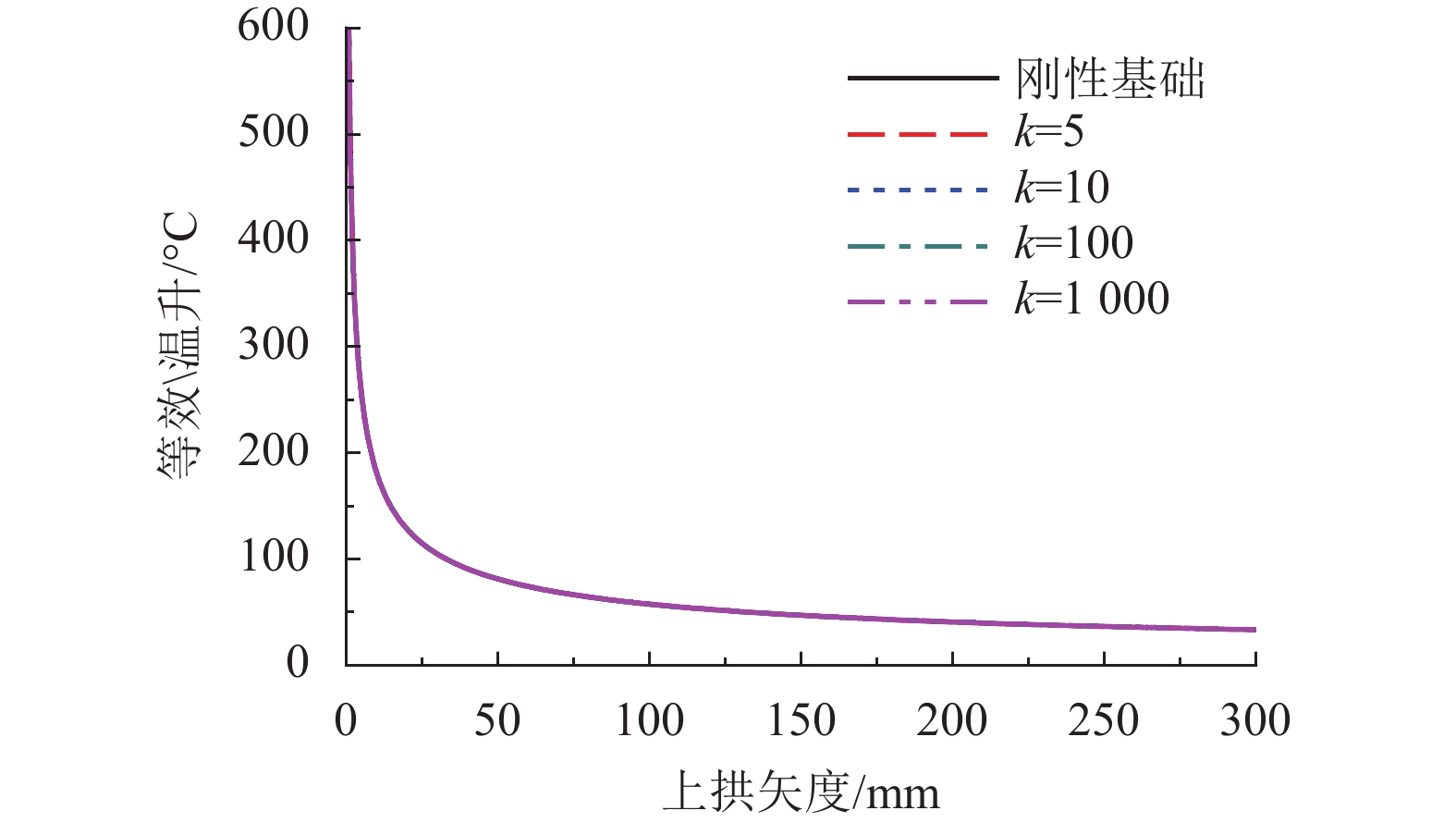
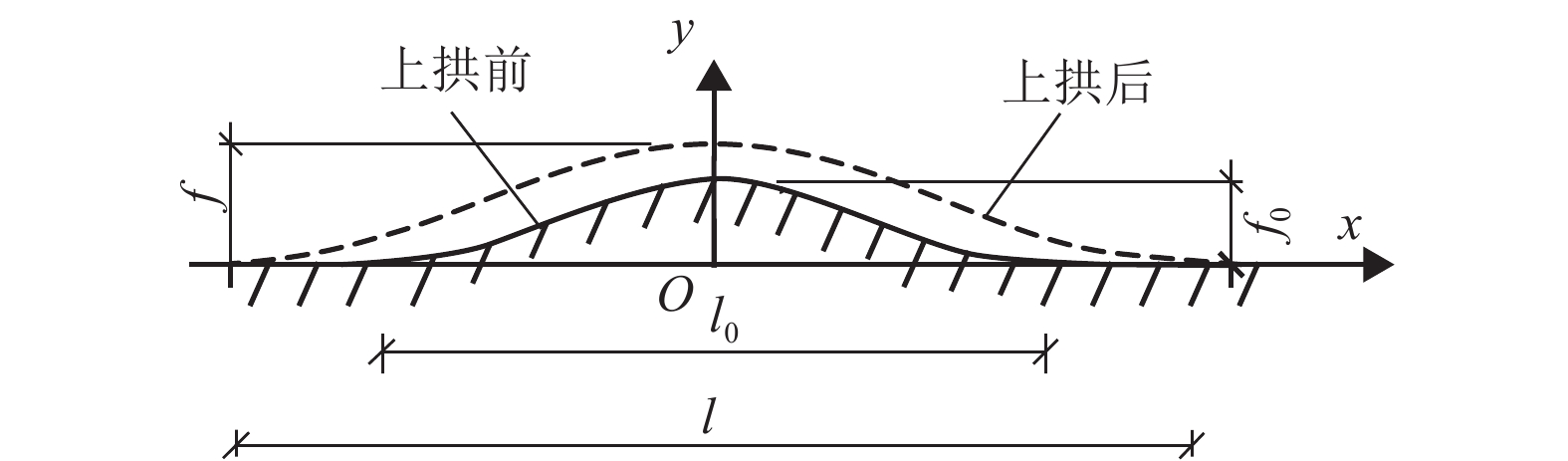
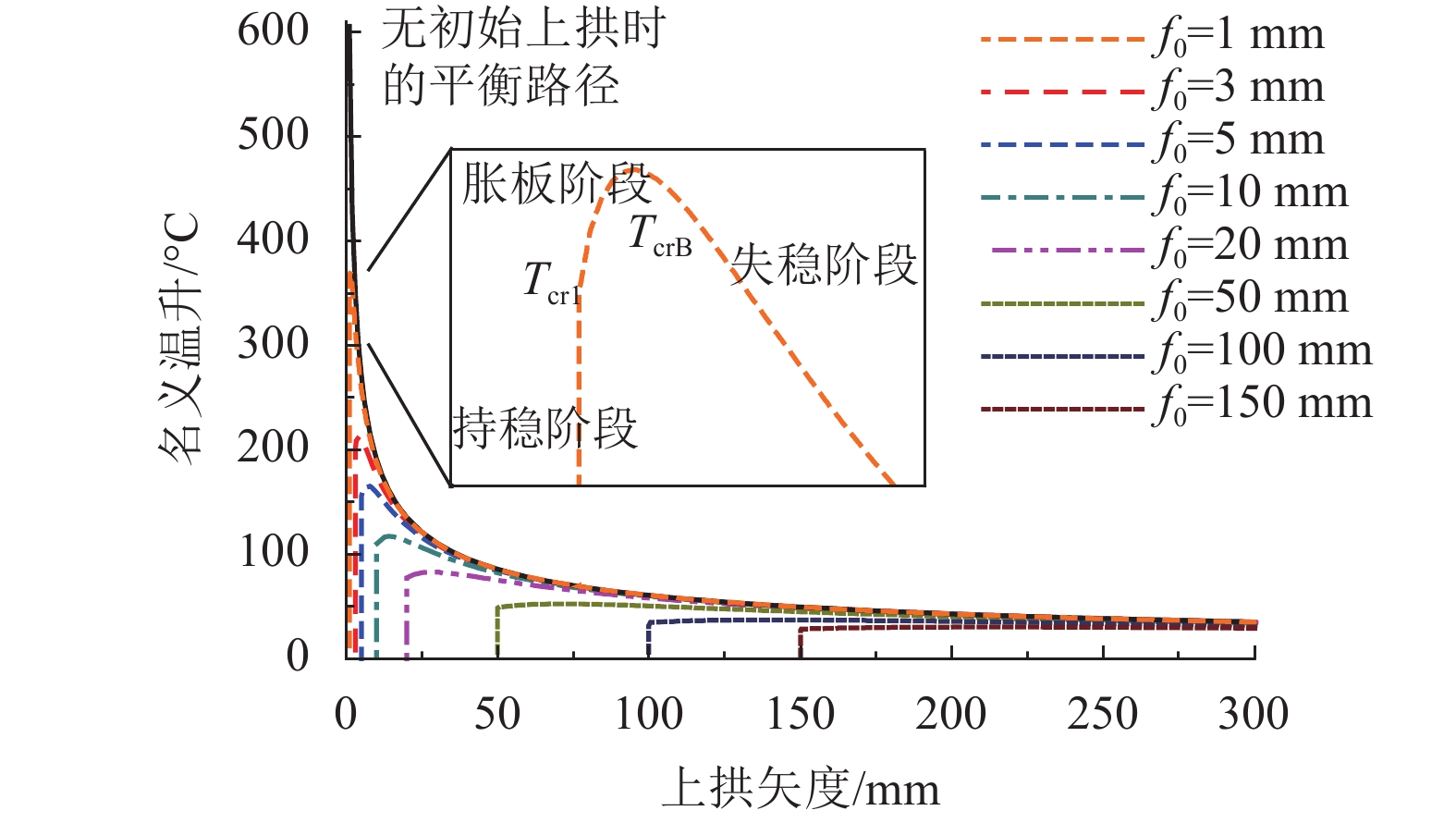
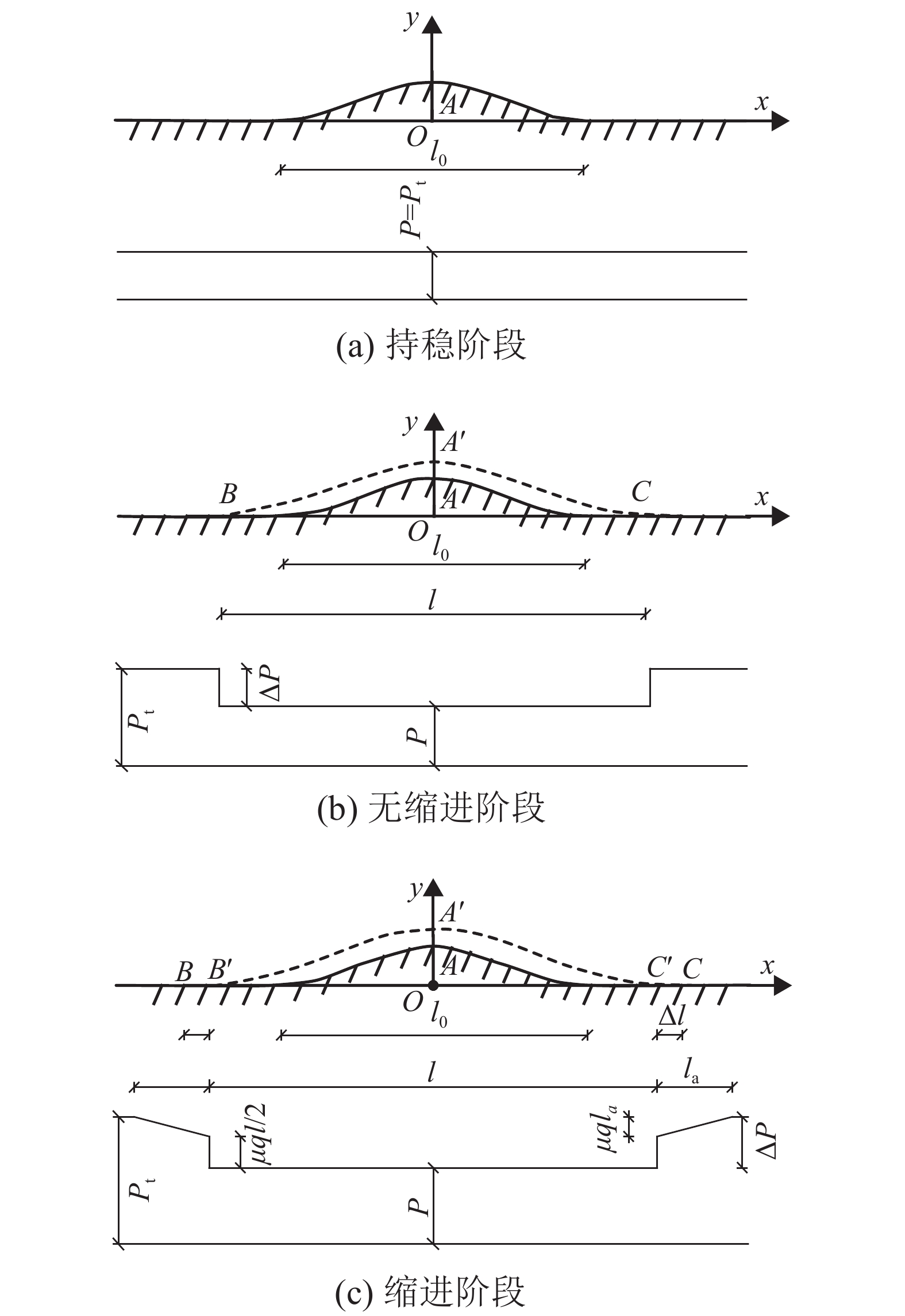
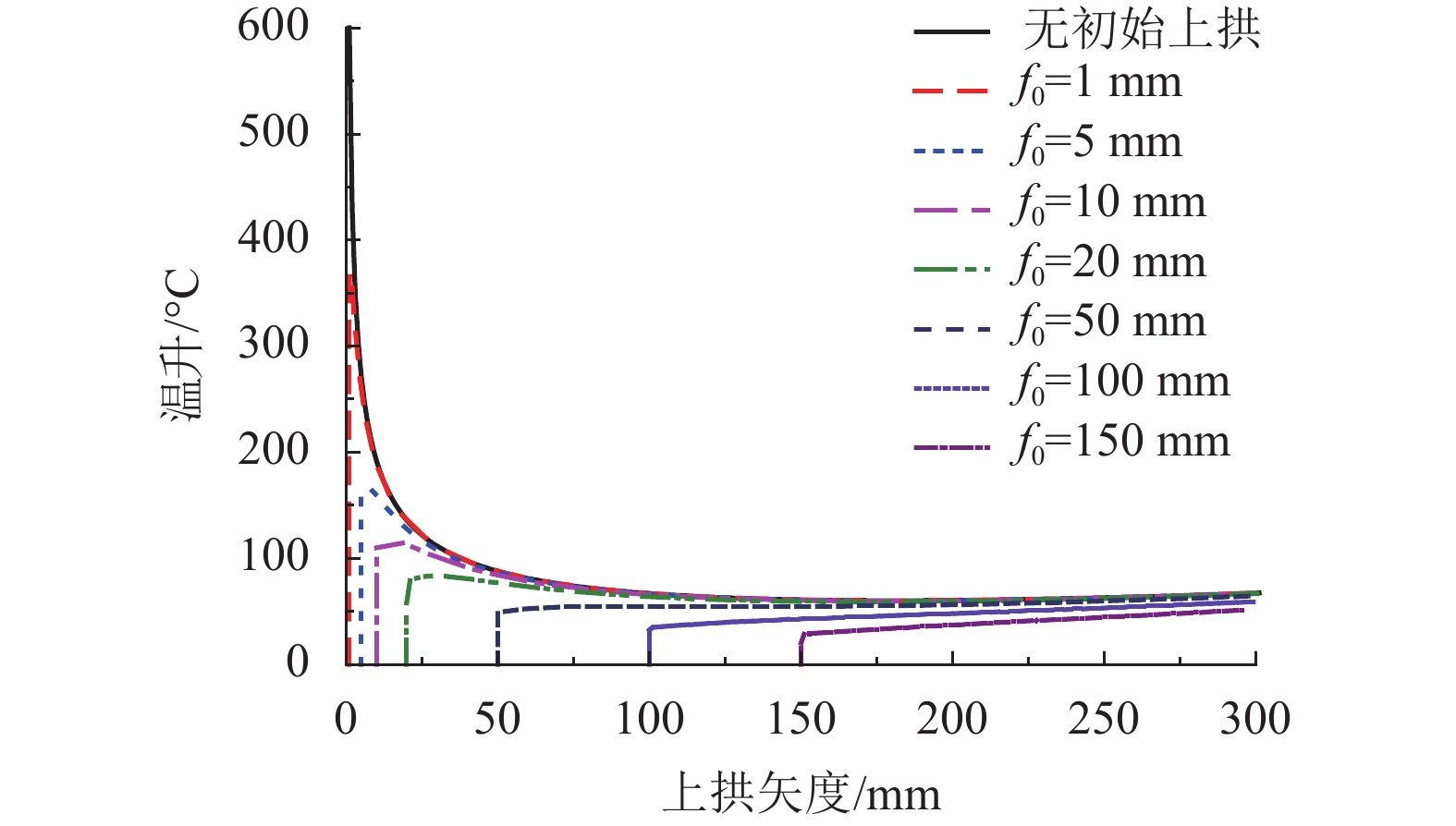
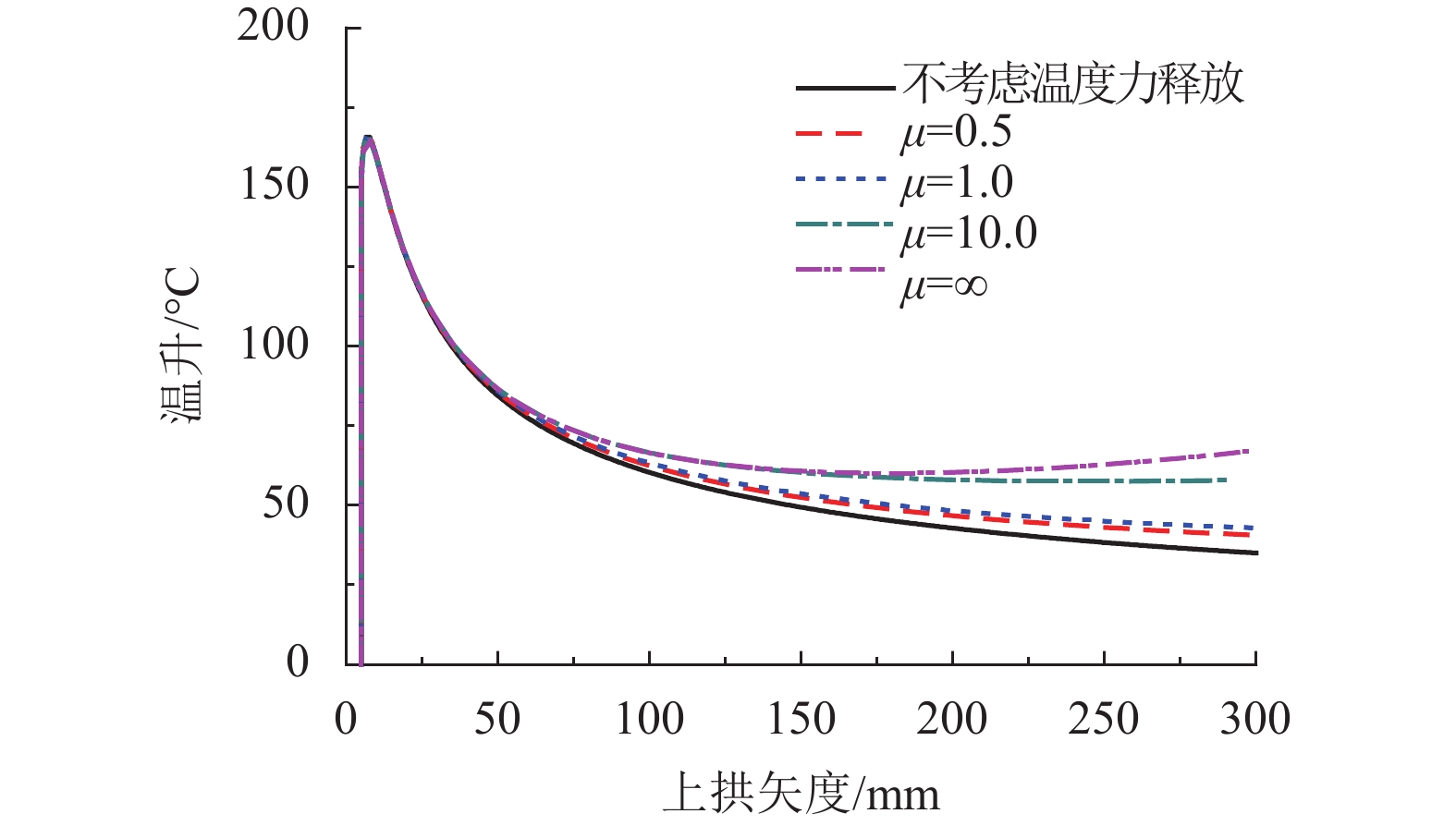
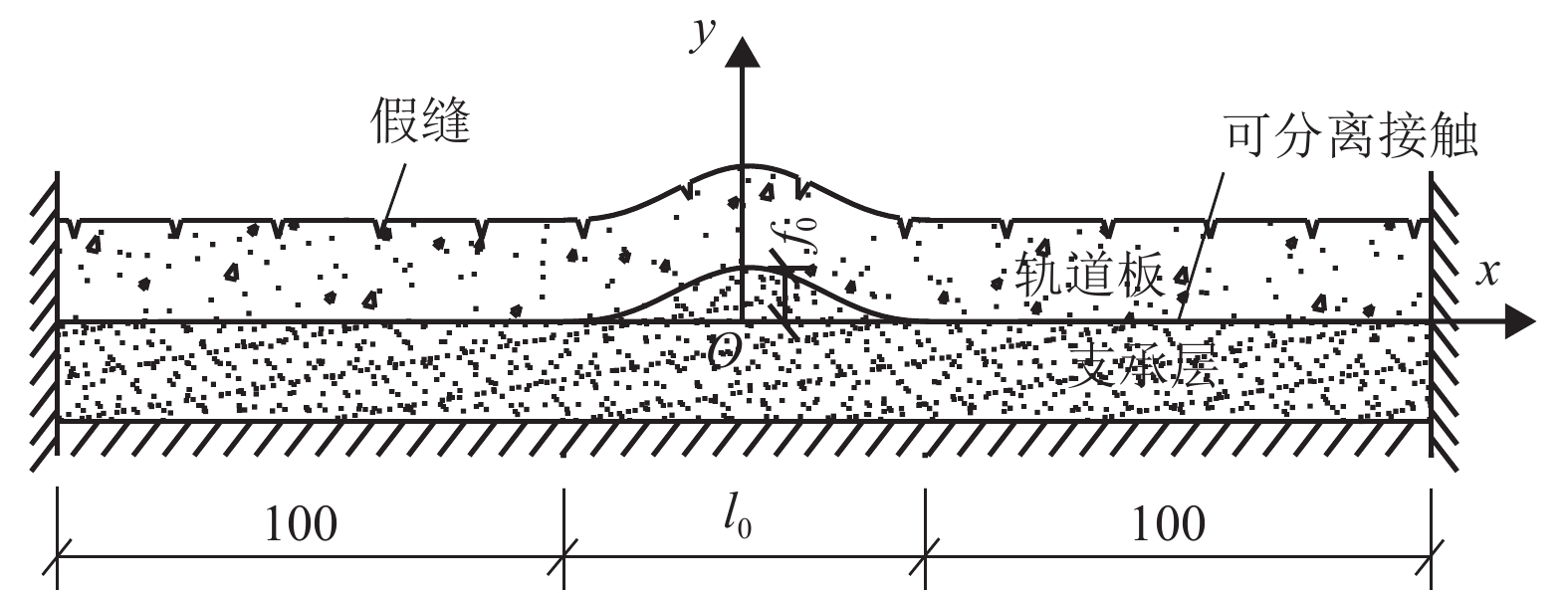
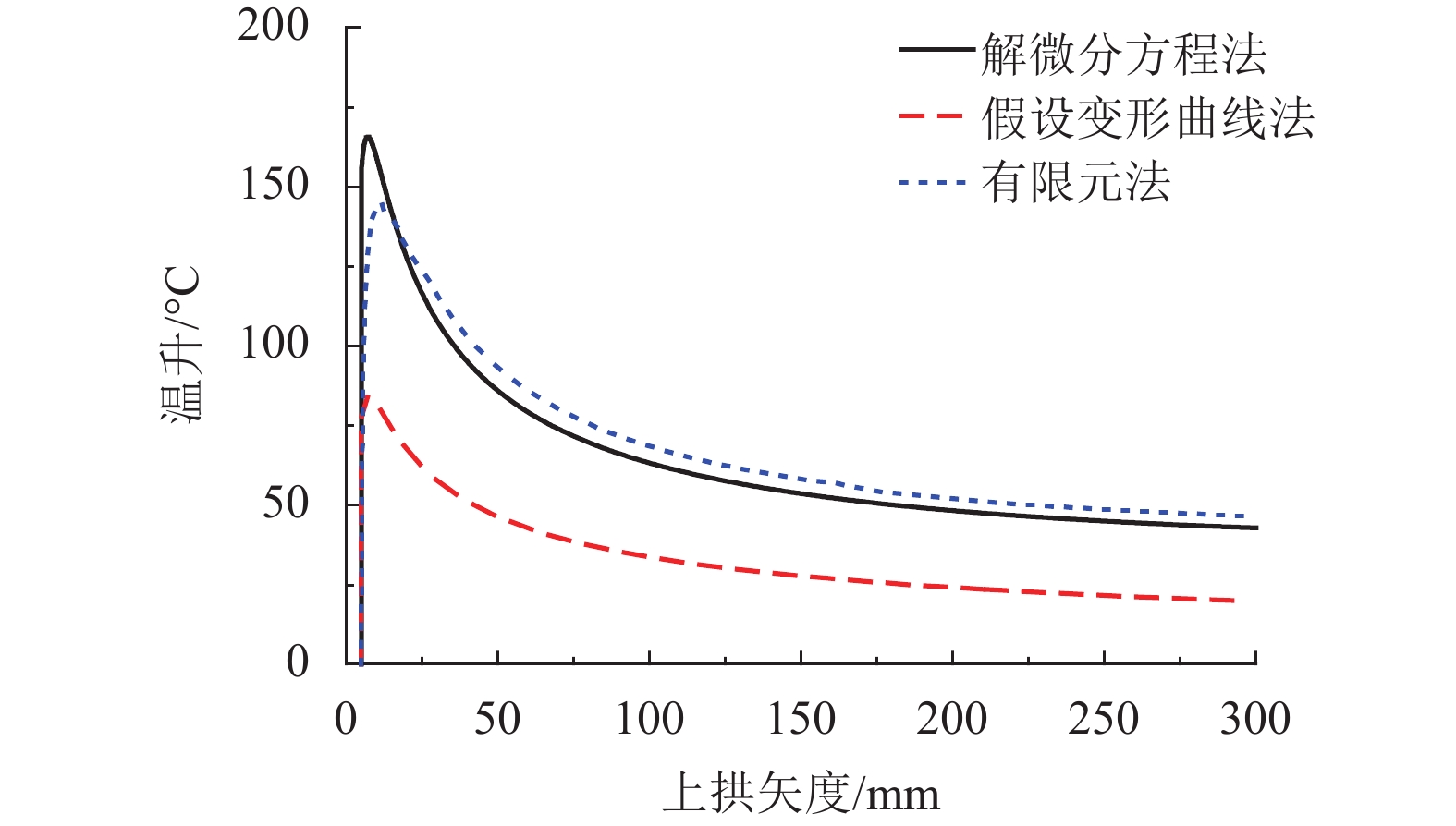
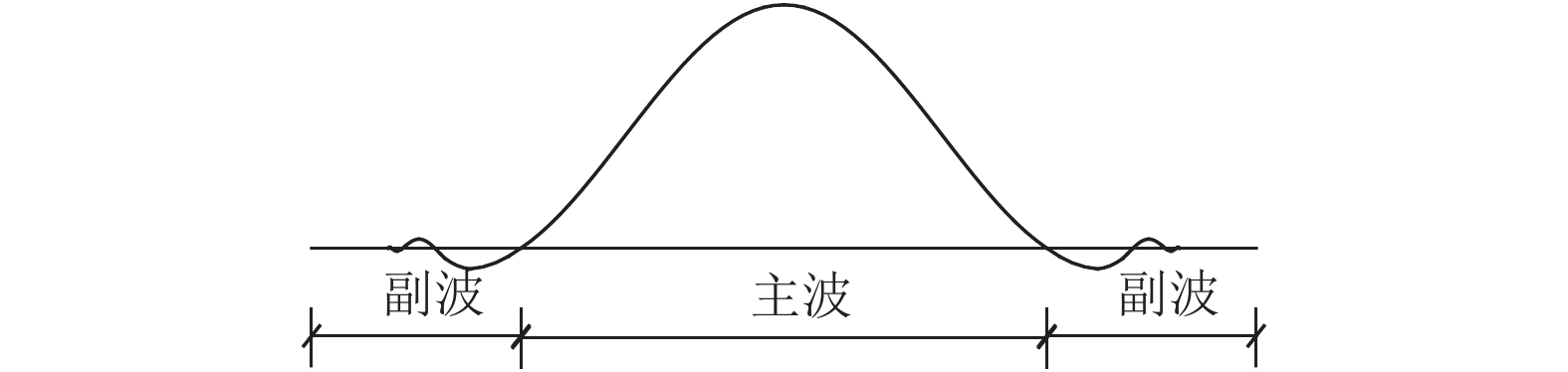
摘要: 为研究纵连式无砟轨道垂向失稳的形态和过程，基于欧拉梁挠曲微分方程推导了温度作用下轨道板上拱波形曲线，得到了上拱矢度与波长的关系；并利用势能驻值原理分析了存在初始上拱时轨道板垂向失稳的平衡路径. 研究表明：与假设变形法相比，解微分方程法精度更高，误差可降低近30%；轨道板的失稳过程包括持稳、胀板和失稳3个阶段，且初始上拱矢度越大，轨道板的持稳极限和胀板极限越小；分析了温度力释放对轨道板上拱平衡路径的影响，表明轨道板失稳的平衡路径会出现强化阶段，且摩擦因数越大，强化阶段出现越早，但变形较小时，温度力释放对轨道板板上拱的影响极小；初始上拱矢度越大，轨道板允许上拱越大，初始上拱小于50 mm时，轨道板难以发生垂向的失稳.
- 纵连式轨道 /
- 轨道板 /
- 温度作用 /
- 稳定性
Abstract: To study the vertical instability form and process of a longitudinal continuous ballastless track, the arch curve of the slab that is influenced by temperature can be deduced based on the deflection differential equation of the Euler beam. The equation of the arch camber and wavelength of the slab was obtained from the arch curve. The equilibrium path of the slab with the initial arch was analysed based on stationary potential energy. Compared with the method of assuming a deformation, the method of solving differential equations is more accurate, and the error is reduced by nearly 30%. The course can be divided into three stages: steady, expansion, and destabilization. The limit of the steady and expansion stages decreases along with the increase of the initial arch camber. The effect of the release of slab temperature on the equilibrium path shows that the path appears as a stiffening stage, and the larger the friction coefficient, the earlier the stage occurs, whereas it has little effect when the deformation is small. The larger the initial camber, the greater the allowed wavelength is. When the initial arch is smaller than 50 mm, the vertical instability of the slab does not occur.
- continuous track /
- slab /
- temperature effect /
- stability

HTML全文

图 1 弹性基础上轨道板的上拱模态

Figure 1. Upper arch modality of slab based on elasticity

下载: 全尺寸图片幻灯片

图 2 力学模型

Figure 2. Mechanical model

下载: 全尺寸图片幻灯片

图 3 不平衡力系数随k的变化

Figure 3. Imbalance force coefficient changes with k

下载: 全尺寸图片幻灯片

图 4 上拱矢度与等效温升的关系

Figure 4. Relationship between upper arch and equivalent temperature rise

下载: 全尺寸图片幻灯片

图 5 轨道板上拱前后的线型

Figure 5. Form of slab before and after arch course

下载: 全尺寸图片幻灯片

图 6 板的平衡路径

Figure 6. Balance path of slab

下载: 全尺寸图片幻灯片

图 7 持稳极限与胀板极限的变化

Figure 7. Variation of stability limit and expansion limit

下载: 全尺寸图片幻灯片

图 8 轨道板纵向压力分布

Figure 8. Longitudinal pressure distribution of slab

下载: 全尺寸图片幻灯片

图 9 考虑温度力释放的平衡路径

Figure 9. Equilibrium path considering release of temperature force

下载: 全尺寸图片幻灯片

图 10 温度力释放的影响

Figure 10. Effect of temperature force release

下载: 全尺寸图片幻灯片

图 11 轨道板上拱的有限元模型（单位：m）

Figure 11. Finite-element model of slab with arch (unit：m)

下载: 全尺寸图片幻灯片

图 12 3种方法的对比

Figure 12. Comparison of three methods

下载: 全尺寸图片幻灯片

表 1 主要计算参数

Table 1. Main calculation parameters

参数	取值	参数		取值
密度/（kg•m^–3）	2 500	横断面面积/m²	0.51
弹性模量/Pa	3.55×10¹⁰	宽度/m	2.55
线膨胀系数	1×10^–5	厚度/m	0.2
重力荷载/（N•m^–1）	12 507.75	惯性矩/m⁴	1.7×10^–3

下载: 导出CSV

表 2 最大上拱位移

Table 2. Maximum camber displacement

f₀	1	5	10	20	50	100	150
最大上拱位移	0	0	0	0	2.4	失稳	失稳

下载: 导出CSV

参考文献(19)

GERE J M, TIMOSHENKO S P. Mechanics of material[M]. New York: Van Nostrand Reinhpld. 1984: 4-15

陈铁云,沈惠申.结构的屈曲[M]. 上海: 上海科学技术文献出版社, 1993: 9-25

KWON I K. Analytical structural stability evaluation for h-section beams made of ordinary structural steels based on boundary conditions at high temperatures[J]. Fire Science and Engineering, 2015, 29(4): 33-38

范峰,严佳川,曹正罡. 考虑杆件失稳影响的网壳结构稳定性研究[J]. 土木工程学报,2012(5): 8-17

FAN Feng, Yan Jiachuan, Cao Zhenggang. Study on stability of reticulated shell structures considering the influence of member buckling[J]. China Civil Engineering Journal, 2012(5): 8-17

班慧勇. 高强度钢材轴心受压构件整体稳定性能与设计方法研究[D]. 北京: 清华大学, 2012

罗永峰,刘慧娟,韩庆华. 弦支穹顶结构动力稳定性分析方法[J]. 西南交通大学学报,2008,43(6): 729-735

LUO Yongfeng, LIU Huijuan, HAN Qinghua. Analysis method of dynamic stability of suspended-dome structures[J]. Journal of Southwest Jiaotong University, 2008, 43(6): 729-735

王骑,廖海黎,李明水,等. 大跨度桥梁颤振后状态气动稳定性[J]. 西南交通大学学报,2013,48(6): 983-988

WANG Qi, LIAO Haili, LI Mingshui, et al. Aerodynamic stability of long-span bridges in post flutte[J]. Journal of Southwest Jiaotong University, 2013, 48(6): 983-988

谭社会. 高温条件下CRTSⅡ型板式无砟轨道变形整治措施研究[J]. 铁道建筑,2016,5: 23-27

TAN Shehui. Study on deformation treatment measures for crtsⅡslab-type ballastless track in high temperature condition[J]. Railway Engineering, 2016, 5: 23-27

曾毅. 纵连式轨道板垂向稳定性研究[D]. 成都: 西南交通大学, 2014

施若苇. 海底管道热屈曲及管土相互作用研究[D]. 杭州: 浙江大学, 2014

HOBBS R E. In-service buckling of heated pipelines[J]. Journal of Transportation Engineering, ASCE, 1984, 110(2): 175-189

TAYLOR N, GAN A B. Submarine pipeline buckling imperfection studies[J]. Thin-Walled Structures, 1986(4): 295-323

HOBBS R E. The effect of soil modulus on pipeline stresses[J]. Journal of the Transportation Engineering Division,ASCE, 1980, 110(6): 775-786

广钟岩. 铁路无缝线路[M]. 北京: 中国铁道出版社, 2005: 5-41

闫斌,戴公连. 高速铁路斜拉桥上无缝线路纵向力研究[J]. 铁道学报,2012,34(3): 83-87

YAN Bin, Dai Gonglian. CWR longitudinal force of cable-stayed bridge of high-speed railway[J]. Journal of the China Railway Society, 2012, 34(3): 83-87

徐玉坡,梁晨,卢耀荣. 设计规范中统一无缝线路稳定性计算公式存在的问题分析[J]. 铁道建筑,2014(5): 124-125

XU Yupo, LIANG Chen, LU Yaorong. The problem in unified calculating formula of CWR stability in the design specification[J]. Railway Engineering, 2014(5): 124-125

周凌远,李乔,李彤梅,等. 改进弧长法求解屈曲问题[J]. 西南交通大学学报,2011,46(6): 922-925

ZHOU Linyuan, Li Qiao, Li Tongmei, et al. Improved arc-length method for solving buckling problem[J]. Journal of Southwest Jiaotong University, 2011, 46(6): 922-925

ALHAYANI A A, RODRíGUEZ J, MERODIO J. Numerical analysis of neckand bulge propagation in anisotropic tubes subject to axial loading and internal pressure[J]. Finite Elements in Analysis & Design, 2014, 90(6): 11-19

林超. 持续高温对CRTSⅡ型板式无砟轨道温度场影响的试验研究[J]. 铁道建筑,2016(5): 15-18

LIN Chao. Experiment study on influence of sustained high temperature on temperature field of CRTSⅡ slab-type ballastless track[J]. Railway Engineering, 2016(5): 15-18

施引文献

附加材料(0)

访问统计