Study On the Crack Plastic Zone of Bridge Structure Steel and Its Application
-
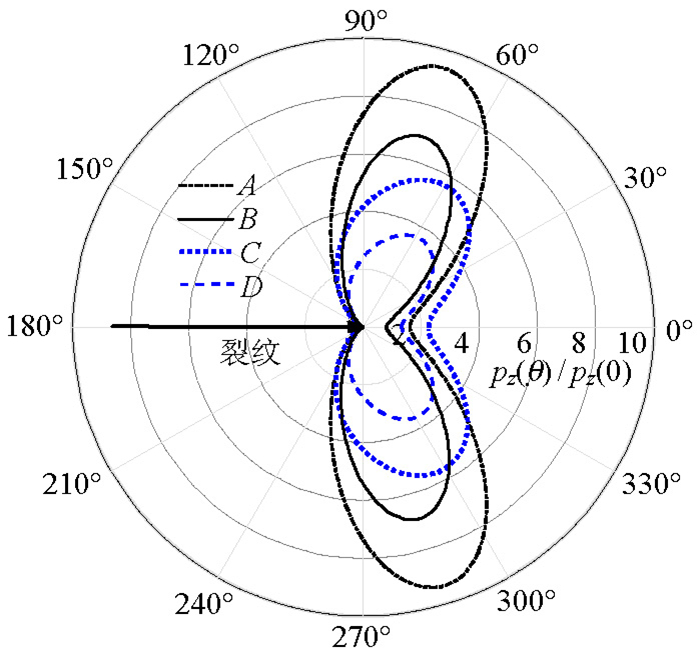
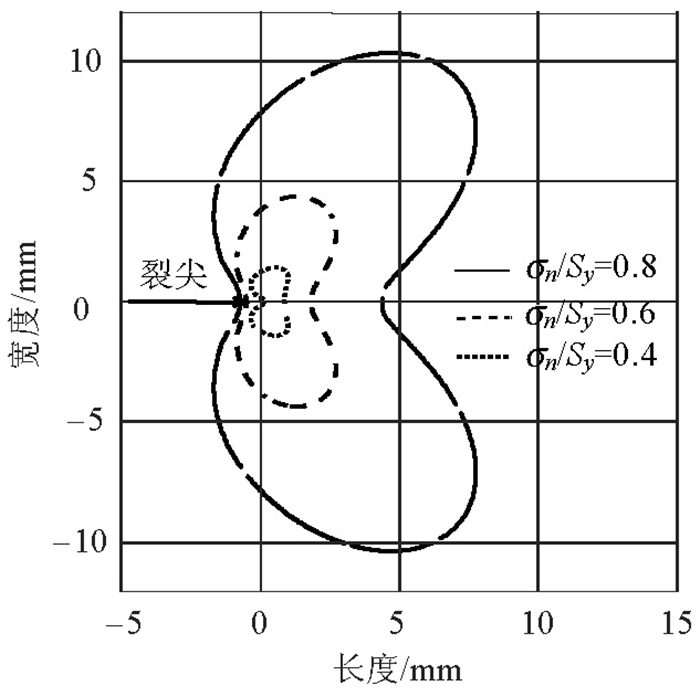
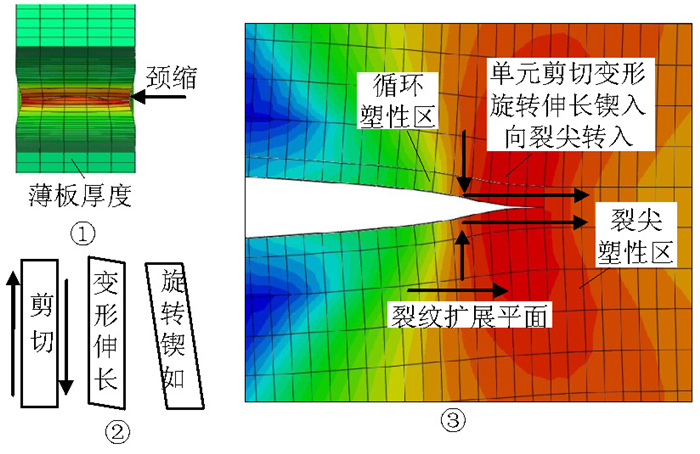
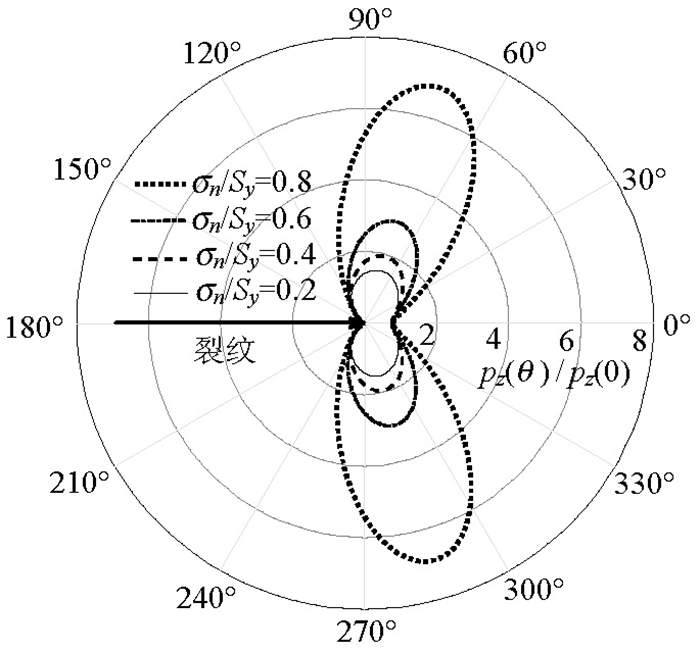
摘要: 为了研究裂纹塑性对裂纹扩展的影响，利用工程简化算法、应力函数法、扩展有限元法对桥梁钢裂尖塑性区的尺寸和形状分别进行了计算；由于平面应力和平面应变情况下尾迹场循环塑性的特性不同，利用不连续扩展有限元对两种情况下尾迹场的循环塑性和塑性累积进行了模拟分析，探讨了裂尖塑性区、循环塑性区的形成和尾迹场产生压应力的机理.研究结果表明：裂尖塑性区尺寸与应力水平（名义应力与屈服极限的比值）的平方成正比，当应力水平大于0.4时，裂尖塑性区尺寸需要考虑应力水平的影响；裂尖塑性区的形状以蝶形向前伸展，使裂纹尾迹场免受裂尖高应力场的拉伸作用，有利于裂纹闭合；裂尖塑性区存在材料的逆向流动，在循环塑性区裂纹表面的塑性累积产生压应力效应有利于裂纹提前闭合，这种塑性诱发的裂纹提前闭合对研究变幅加载、过载引起的裂纹扩展滞后有重要意义.Abstract: In order to study the influence of crack plasticity on crack growth, the shape and size of crack tip plastic zone of bridge steel were calculated by using engineering simplification algorithm, the stress function method and extended finite element method respectively. As a result of the cyclic plasticity of wake field under plane stress and plane strain being different, cyclic plasticity and plastic accumulation of crack tip and wakes were simulated and analyzed by using the discontinuous extended finite element method. The formation of crack tip plastic zone, cyclic plastic zone and the mechanism of compressive stress of wake field were studied. The results showed that the appearances and sizes of plastic zone at the crack tip were proportional to the square of the stress level (the ratio of nominal stress to the yield limit). When the stress level was greater than 0.4, the size of the crack tip plastic zone had to be taken into account the effect of the stress level. The butterfly-shaped crack tip plastic zone symmetrically extended forward, shielding the tensile force of the crack tip high stress field on the wake field, which was beneficial to crack closure. There exists reverse flow of material in plastic zone of crack tip. The compressive stress effect induced by the plastic accumulation on the crack surface was beneficial to the crack closure in advance. Crack closure produced by plasticity had an important influence on the retardation of crack extension in the case of variation load and overload.
-
图 2 由应力函数计算的Ⅰ型裂纹裂尖塑性区结果
Figure 2. Estimated resultsfrom stress function for the mode Ⅰ
图 3 Ⅰ型裂纹裂尖塑性区平衡校正前后的结果比较
Figure 3. Comparison of crack tip plastic zone before and after equilibrium correction for mode Ⅰ crack
图 4 不同应力比情况下中心裂纹塑性区
Figure 4. Central crack plastic zone under different stress ratios
表 1 各种计算方法的塑性半径比较
Table 1. Comparison of plastic radii of calculation methods
mm 计算方法 修正前后 σn/Sy 0.8 0.6 0.4 KI+T 前 3.20 1.80 0.80 后 6.40 3.60 1.60 Westergoard函数 前 4.03 2.27 1.01 后 8.06 4.54 2.02 XFEM — 4.28 1.72 0.70 
下载: 导出CSV
-
李传习, 李游, 陈卓异, 等.钢箱梁横隔板疲劳开裂原因及补强细节研究[J].中国公路学报, 2017, 30(3):121-131. doi: 10.3969/j.issn.1001-7372.2017.03.013LI Chuanxi, LI You, CHEN Zhuoyi, et al. Fatigue cracking reason and detail dimension of reinforcement about transverse diaphragm of steel box bridge[J]. China Journal of Highway and Transport. 2017, 30(3):121-131. doi: 10.3969/j.issn.1001-7372.2017.03.013 张清华, 卜一之, 李乔.正交异性钢桥面板疲劳问题的研究进展[J].中国公路学报, 2017, 30(3):14-30. doi: 10.3969/j.issn.1001-7372.2017.03.002ZHANG Qinghua, BU Yizhi, LI Qiao. Review on fatigue problems of orthotropic steel bridge deck[J]. China Journal of Highway and Transport, 2017, 30(3):14-30. doi: 10.3969/j.issn.1001-7372.2017.03.002 CARROLL J D, ABUZAID W Z, LAMBROS J, et al. On the interactions between strain accumulation, microstructure, and fatigue crack behavior[J]. International Journal of Fracture, 2013, 180(2):223-241. doi: 10.1007/s10704-013-9813-8 MIAO Jiashi, POLLOCK T M, WAYNE JONES J. Microstruc-tural extremes and the transition from fatigue crack initiation to small crack growth in a polycrystalline nickel-base superalloy[J]. Acta Materialia, 2012, 60(6/7):2840-2854. GROSS D W, NYGREN K, PATAKY G J, et al. The evolved microstructure ahead of an arrested fatigue crack in Haynes 230[J]. Acta Materialia, 2013, 61(15):5768-5778. doi: 10.1016/j.actamat.2013.06.020 PILCHAK A L. Fatigue crack growth rates in alpha titanium:faceted vs. striation growth[J]. Scripta Materialia, 2013, 68(5):277-280. doi: 10.1016/j.scriptamat.2012.10.041 HERBIG M, KINGM A, REISCHIG P, et al. 3-D growth of a short fatigue crack within a polycrystalline microstructure studied using combined diffraction and phase-contrast X-ray tomography[J]. Acta Materialia, 2011, 59(2):590-601. doi: 10.1016/j.actamat.2010.09.063 WILLIAMS J J, YAZZIE K E, PADILLA E, et al. Understanding fatigue crack growth in aluminum alloys by in situ X-ray synchrotron tomography[J]. International Journal of Fatigue, 2013, 57(12):79-85. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=4c542d5e9d25f4f34e878af929f5f164 陈景杰, 黄一, 李玉刚.压应力对裂尖塑性区影响的量化研究[J].华中科技大学学报:自然科学版, 2016(2):102-106. http://d.old.wanfangdata.com.cn/Periodical/hzlgdxxb201602021CHEN Jingjie, HUANG Yi, LI Yugang. Quantitative study on the influence of compressive stress on crack tip plastic zone[J]. Journal of Huazhong University of Science and Technology:Nature Science Edition, 2016(2):102-106. http://d.old.wanfangdata.com.cn/Periodical/hzlgdxxb201602021 赵均海, 魏雪英, 马淑芬.混凝土结构Ⅰ型裂纹裂尖塑性区研究[J].工程力学, 2006, 23(9):141-145. doi: 10.3969/j.issn.1000-4750.2006.09.024ZHAO Junhai, WEI Xueying, MA Shufen. Crack tip plastic zone of type Ⅰ cracks for concrete structure[J]. Engineering Machanics, 2006, 23(9):141-145. doi: 10.3969/j.issn.1000-4750.2006.09.024 VASCO OLMO J M, JAMESM M N, CHRISTOPHER C J, et al. Assessment of crack tip plastic zone size and shape and its influence on crack tip shielding[J]. Fatigue & Fracture of Engineering Materials & Structures, 2016, 39(8):969-981. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=4e1acf3a436b9cc7d1d8e42f1908a3fb IRWIN G R. Analysis of stresses and strains near the end of a crack traversing a plate[J]. Journal of Applied Mechanics, 1957, 24:361-364. SANFORD R J. Principles of fracture mechanics[M]. New Jersey:Pearson Education, 2002:29-44. SOUSA R A, CASTRO J T P, LOPES A A O, et al, On improved crack tip plastic zone estimates based on T-stress and on complete stress fields[J]. Fatigue & Fracture of Engineering Materials & Structures, 2012, 36(1):25-38. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CC0213745990 BELYTSCHKO T, GRACIE R, VENTURA G. A review of extended generalized finite element methods for material modeling[EB/OL].[2017-05-12]. http://iopscience.iop.org/article/10.1088/0965-0393/17/4/043001/meta. GRACIE R, WANG Hongwu, BELYTSCHKO T. Blending in the extended finite element method by discontinuous Galerkin and assumed strain methods[J]. International Journal for Numerical Methods in Engineering, 2008, 74(11):1645-1669. doi: 10.1002/(ISSN)1097-0207 PIPPAN R, HOHENWARTER A. Fatigue crack closure:a review of the physical phenomena[J]. Fatigue & Fracture of Engineering Materials & Structures, 2017, 40(4):471-495. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC5445565/ XIANG Yibing, LU Zizi, LIU Yongming. Crack growth-based fatigue life prediction using an equivalent initial flaw model. part Ⅰ:uniaxial loading[J]. International Journal of Fracture, 2010, 32(2):341-349. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0215686284/ IACOVIELLO F, COCCO V D, CAVALLINI M. Fatigue crack propagation and overload damaging micromechanisms in a ferritic-pearlitic ductile cast iron[J]. Fatigue & Fracture of Engineering Materials & Structures, 2016, 39(8):999-1011. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7cc918905a04cc34e9a3ea9c33d5235e HOBBACHER A. XⅢ-2151r1-07/XV-1254r1-07 Recommendation for fatigue design of welded joints and components[S]. Paris: International Institute of Welding, 2007. 刘艳萍, 陈传尧, 李建兵, 等.14MnNbq焊接桥梁钢的疲劳裂纹扩展行为研究[J].工程力学, 2008, 25(4):209-213. http://d.old.wanfangdata.com.cn/Periodical/gclx200804036LIU Yanping, CHEN Chuanyao, LI Jianbing, et al. Fracture crack growth behavior for the weld heat-affected zone of 14MnNbq bridge steel[J]. Engineering Mechanics, 2008, 25(4):209-213. http://d.old.wanfangdata.com.cn/Periodical/gclx200804036 El HADDAD M H, TOPPER T H, SMITH K N. Prediction of non propagating cracks[J]. Engineering Fracture Mechanics, 1979, 11(3):573-584. doi: 10.1016/0013-7944(79)90081-X 中交公路规划设计院有限公司. JTG D64-2015公路钢结构桥梁设计规范[S].北京: 人民交通出版社股份有限公司, 2015. -
下载:
点击查看大图
图(6) / 表(1)
计量
- 文章访问数: 461
- HTML全文浏览量: 214
- PDF下载量: 167
- 被引次数: 0