Earthquake Risk Assessment of Bridge Based on Failure Probability Method
-
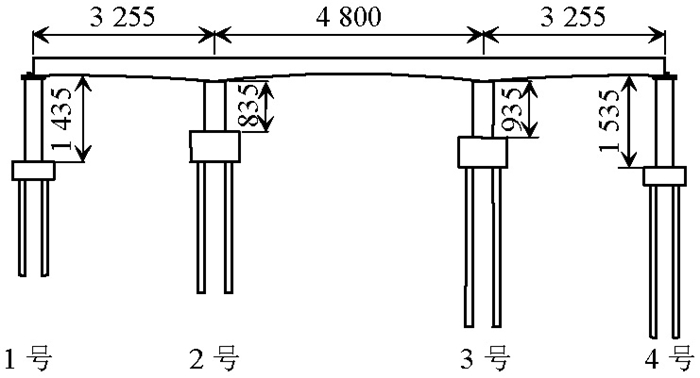
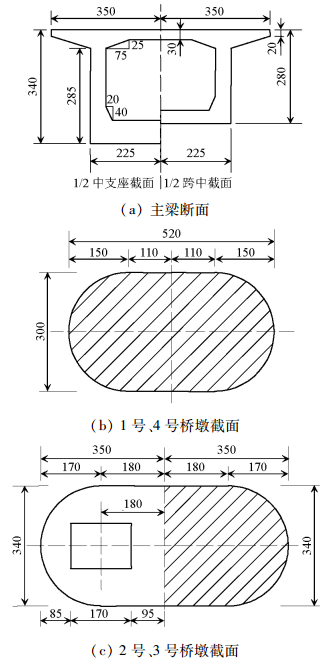
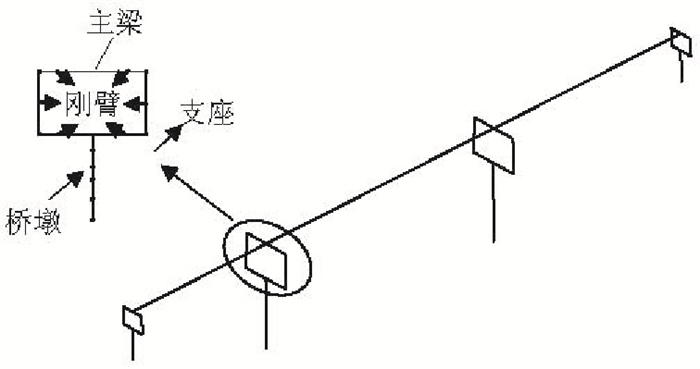
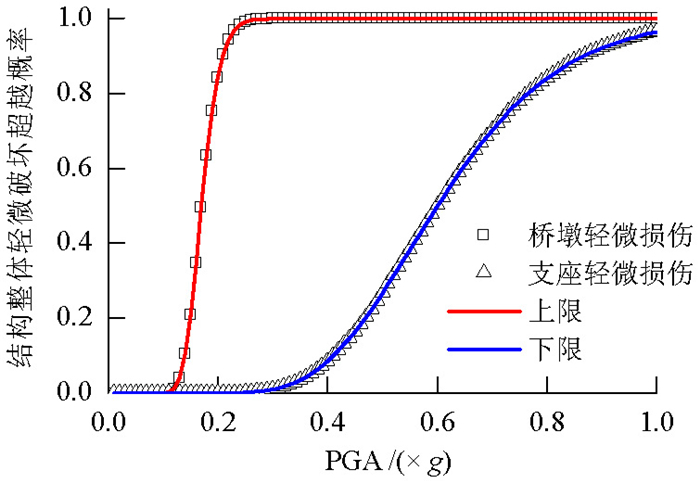
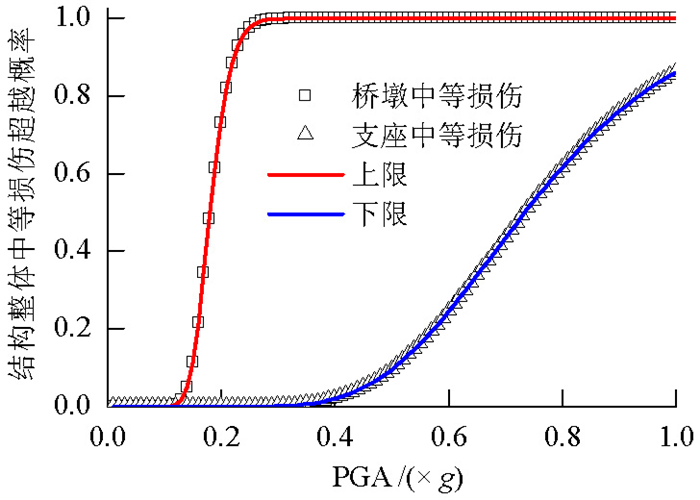
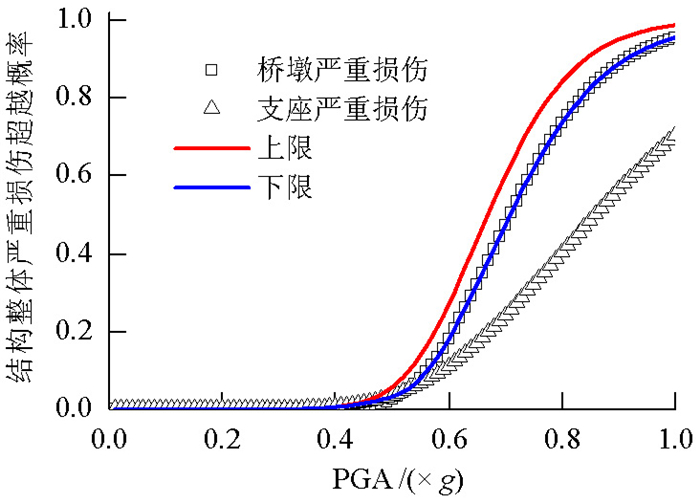
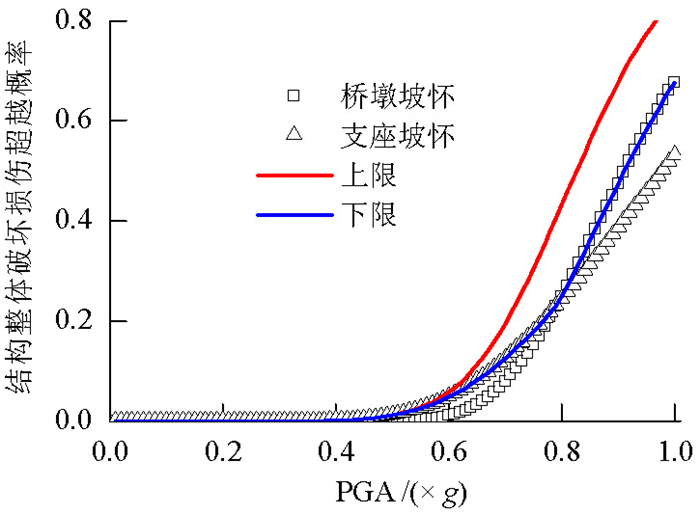
摘要: 为了研究地震破坏下高速铁路连续梁桥发生破坏的可能性,根据地震风险性(risk)为地震危险性(hazard)与易损性(fragility)乘积的定义,基于失效概率法,对高速铁路连续梁桥地震风险评估方法进行了分析.通过条带法建立桥梁地震需求模型,基于可靠度函数获得桥梁地震易损性曲线,拟合得到桥梁易损性概率密度函数;根据桥址处地震危险性资料,推导桥址处地震加速度概率密度函数;通过地震加速度概率密度函数与桥梁结构易损性概率密度函数的数值积分,实现桥梁地震风险概率评估.以一座(32+48+32)m高速铁路连续梁桥为例系统演绎了失效概率法桥梁风险评估的实现过程.研究结果表明:当地震危险性资料缺乏或不足时可以通过地震烈度分布函数及其与地震峰值加速度之间的换算关系,推导和完善地震危险性分析资料;对于高速铁路(32+48+32)m连续梁桥100年设计期间内发生轻微损伤的概率为5.16%,发生中等损伤的概率为4.46%,桥梁受到轻微损伤和中等损伤风险概率接近,几乎不可能发生严重损伤和完全破坏.Abstract: To study the possibility of destruction of a high-speed railway continuous girder bridge under the influence of seismic damage, a seismic risk assessment of the bridge was conducted. The failure probability method was used, in which seismic risk is defined as the product of seismic hazard and fragility (i.e., seismic risk=seismic hazard×fragility). The bridge seismic demand model was established using the strip coating method. The bridge seismic fragility curve was obtained based on the reliability function, and the probability density function of the bridge fragility was fitted. According to seismic risk data of the bridge site, the probability density function of seismic acceleration of the bridge site was derived. The probability density function of seismic acceleration was numerically integrated with that of the bridge structural vulnerability to accomplish the probability evaluation of the bridge earthquake risk. Taking a (32+48+32) m high-speed railway continuous girder bridge as an example, the system conducted the bridge risk assessment using the failure probability method. The results show that when earthquake risk data are lacking or insufficient, it is possible to deduce and improve seismic risk analysis data using the conversion relation between the earthquake intensity distribution function and the seismic peak acceleration. For the high-speed railway (32+48+32) m continuous girder bridge, within 100 years of use, the occurrence probability of slight damage is 5.16% and that of secondary damage is 4.46%. The probabilities of slight damage and secondary damage risk of the bridge are similar, whereas the probabilities of serious damage and complete destruction are very small, indicating that serious damage and complete destruction are almost impossible.
-
表 1 支座刚度
Table 1. Bearing stiffness
支座位置 支反力/MN 支座刚度/(MN·m-1) 1号墩 5.4 54 2号墩 39.0 390 3号墩 39.0 390 4号墩 5.4 54 表 2 桥墩破坏状态定义
Table 2. Definition of pier damage states
损伤状态 损伤准则 基本完好 ϕ≤ϕ1 轻微损伤 ϕ1<ϕ≤ϕ2 中等损伤 ϕ2<ϕ≤ϕ3 严重损伤 ϕ3<ϕ≤ϕ4 结构破坏 ϕ>ϕ4 表 3 桥墩不同状态破坏指标
Table 3. Different piers damage criteria
方向 墩号 ϕ1/×10-4 ϕ2/×10-4 ϕ3/×10-3 ϕ4/×10-3 顺向 3号 7.44 8.52 16.80 29.10 1号 4.82 6.24 8.87 11.90 横向 2号 3.63 4.44 6.21 7.76 3号 3.64 4.45 6.12 7.64 4号 4.84 6.24 8.73 11.70 表 4 支座破坏状态定义
Table 4. Definition of bearing damage states
损伤状态 损伤准则 基本完好 D≤150 mm 轻微损伤 150 mm<D≤200 mm 中等损伤 200 mm<D≤250 mm 严重损伤 250 mm<D≤300 mm 完全破坏 D>300 mm 表 5 桥梁整体易损性概率密度函数拟合参数
Table 5. Fitting parameters of overall fragility probability density function
拟合参数 轻微损伤 中等损伤 严重损伤 破坏 α 1.004 7 1.005 6 1.014 0 1.016 5 λ -1.008 9 -1.009 9 -1.015 9 -1.017 3 δ 1.670 7 1.778 8 6.581 4 8.121 9 u 10.408 3 10.414 1 9.143 9 8.542 6 表 6 地震危险性资料
Table 6. Seismic hazard information
对应峰值加速度/(×g) 发生概率 0.001 95 0.999 9 0.003 91 0.999 9 0.007 82 0.999 9 0.015 64 0.999 9 0.031 27 0.969 2 0.062 54 0.618 2 0.125 01 0.189 9 0.250 17 0.032 3 0.500 30 0.003 0 1.000 30 0.000 1 表 7 桥梁风险概率
Table 7. Bridge risk probability
破坏程度 轻微损伤 中等损伤 严重损伤 完全破坏 风险概率 0.051 64 0.044 57 4.711×10-4 2.634×10-4 -
CORNELL C A. Risk-based structural design[C]//Proceedings of Symposium on Risk Analysis.[S.l.]: Press of University of Michigan, 1994: 37-48. LUPOI A, FRANCHIN P, SCHOTANUS M. Seismic risk evaluation of RC bridge structure[J]. Earthquake Engineering and Structural Dynamics, 2003, 32(8):1275-1290. doi: 10.1002/(ISSN)1096-9845 BRADLEY B A, DHAKAL R P. Error estimation of closed-form solution for annual rate of structural collapse[J]. Earthquake Engineering and Structural Dynamics, 2008, 37(5):1721-1737. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=5487de2708e2cb9aa82dc2df88ca007c KAMESHWAR S, PADGETT J E. Multi-hazard risk assessment of highway bridges subjected to earthquake and hurricane hazards[J]. Engineering Structures, 2014, 78:154-166. doi: 10.1016/j.engstruct.2014.05.016 于晓辉.钢筋混凝土框架结构概率地震易损性与风险分析[D].哈尔滨: 哈尔滨工业大学, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D238821 阮欣, 陈艾荣, 石雪飞.桥梁工程风险评估[M].北京:人民交通出版社, 2008:1-10. 冯清海, 袁万城.基于IDA-MC的桥梁地震风险概率评估方法[J].长安大学学报:自然科学版, 2010, 30(3):60-64. http://www.cnki.com.cn/Article/CJFDTOTAL-XAGL201003015.htmFENG Qinghai, YUAN Wancheng. Method and application of seismic risk probability analysisfor large-long span bridge based on IDA-MC[J]. Journal of Chang'an University:Natural Science Edition, 2010, 30(3):60-64. http://www.cnki.com.cn/Article/CJFDTOTAL-XAGL201003015.htm 张喜刚.公路桥梁和隧道工程设计安全风险评估[M].北京:人民交通出版社, 2010:1-10. 阮欣.桥梁工程风险评估体系及关键问题研究[D].上海: 同济大学, 2006. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1020356 韩兴, 李鑫, 向宝山, 等.基于IDA方法的高速铁路连续梁桥易损性分析[J].公路交通科技, 2016, 33(2):55-59. http://d.old.wanfangdata.com.cn/Periodical/gljtkj201602009HAN Xing, LI Xin, XIANG Baoshan, et al. Analysis of seismic fragility of high speed railway continuous beam bridge based on IDA method[J]. Journal of Highway and Transportation Research and Development, 2016, 33(2):55-59. http://d.old.wanfangdata.com.cn/Periodical/gljtkj201602009 沈怀至.基于性能的混凝土坝-地基系统地震破损分析与风险评价[D].北京: 清华大学, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10003-2009055448.htm 高小旺, 鲍霭斌.地震作用的概率模型及其统计参数[J].地震工程与工程振动, 1985, 5(1):13-22. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000000199396GAO Xiaowang, BAO Aibin. Probabilistic model and its statistical parameters for seismic load[J]. Earth-quake Engineering and Engineering Vibration, 1985, 5(1):13-22. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000000199396 刘恢先.修订我国地震烈度表的一个建议方案[M].北京:科学出版社, 1981:1-13. 过镇海, 时旭东.钢筋混凝土原理和分析[M].北京:清华大学出版社, 2003:167-182. SHINOZUKA M, FENG M Q, LEE J, et al. Statistical analysis of fragility curves[J]. Eng Mech, Trans ASCE, 2000, 126(12):1224-1231. doi: 10.1061/(ASCE)0733-9399(2000)126:12(1224) -






 下载:
下载: