Multiple Model Analysis for Studying Groundwater Uncertainties
-
摘要: 为研究地下水概念模型的构建偏差及水文地质参数非均质性引起的地下水渗流场模拟不确定性问题，首先根据自然条件的差异构建2组概念模型；以大量原位水文地质试验获取的待估参数数据为先验信息，应用接受条件进行调整的马尔科夫链蒙特卡罗方法（MCMC）中的自适应采样算法（A-M）进行参数样本采集，并基于2组概念模型分别构建多组渗流场计算模型；将输出结果基于AICc准则进行相关多模型定量分析.研究结果表明：调整的A-M采样算法，参数样本的遍历性及收敛性未受影响；计算模型中除存在"异参同效"，亦存在"异构同效"；异构同效虽存在，但更接近客观条件的概念模型结构获取高精度模型的概率较大，1#、2#概念模型中方差值介于1~2的模型比例分别为65%、46%；各概念模型的100组计算模型中，剔除Delta值大于10的计算模型后，1#模型中仅保留排名前10个模型，累计后验概率0.996，2#模型则保留排名前21个模型，而其排名前10的模型累计后验概率仅为0.884.Abstract: Multiple Model Analysis was applied to study the groundwater modelling uncertainties caused by the deviation of model structure and heterogeneity in aquifer media. According to different natural conditions, two hydrogeological conceptual models were established. Using a large number of model parameter data, obtained through hydrogeological tests, as a priori information and based on the two conceptual models, a series of seepage field models was constructed using the Adaptive Metropolis-Markov Chain Monte Carlo method that acceptance condition was adjusted. Uncertainties of modelling output data are analysed based on corrected Akaike's Information Criteron. Research indicates that the ergodicity and convergence of sample parameters will not be affected by changes in acceptance conditions. The model output data include the following effects:"same results with different parameters" and "same results with different models". Although these effects exist, the model structure is closer to the objective of improving the probability of obtaining a high precision model. The proportion of the primary conceptual model, with a variance between 1 and 2, is 65%. When the model with Delta values greater than 10 is excluded, the top 10 models are retained and the cumulative a posterior probability is 0.996. The proportion of the second conceptual model, with a variance between 1 and 2, is 46%. When the model with Delta values greater than 10 is excluded, the top 21 models are retained. The cumulative posterior probability of the top 10 models is only 0.884.
-
图 2 研究区同类含水介质水文地质试验孔分布
注: Q4al+pl为第四系全新统河道漫滩、一级阶地冲洪积砂卵砾石层孔隙潜水; Q4alp为第四系全新统山前扇状冲洪积砂卵砾石层孔隙潜水; Q3fgl+al为第四系上更新统河间二级阶地冰-水堆积泥质砂卵砾石层孔隙潜水; Q1+2fgl+al为第四系中、下更新统泥卵砾石孔隙潜水.
Figure 2. Distribution of boreholes at similar aquifers
图 4 1#模型计算模型地下水位众数、95 %置信区间(阴影区域)与观测值
Figure 4. 95 % confidence intervals (shadow areas), observations and mean values
-
吴吉春, 陆乐.地下水模拟不确定性分析[J].南京大学学报:自然科学, 2011, 47(3):227-234. http://d.old.wanfangdata.com.cn/Thesis/Y1859981WU Jichun, LU Le. Uncertainty analysis for groundwater modeling[J]. Journal of Nanjing University:Natural Sciences, 2011, 47(3):227-234. http://d.old.wanfangdata.com.cn/Thesis/Y1859981 陆乐, 吴吉春, 陈景雅.基于贝叶斯方法的水文地质参数识别[J].水文地质工程地质, 2008(5):58-63. doi: 10.3969/j.issn.1000-3665.2008.05.014LU Le, WU Jichun, CHEN Jingya. Identification of hydrogeological parameters based on the Bayesian method[J]. Hydrogeology and Engineering Geology, 2008(5):58-63. doi: 10.3969/j.issn.1000-3665.2008.05.014 BEVEN K, BINLEY A. The future of distributed models-model calibration and uncertainty prediction[J]. Hydrological Processes, 1992, 6(3):279-98. doi: 10.1002/(ISSN)1099-1085 BEVEN K, FREER J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology[J]. Journal of Hydrology, 2001, 249(1):11-29. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=990d8ae736d1912750863bbda2673049 HASSAN A E, BEKHIT H M, CHAPMAN J B. Using Markov Chain Monte Carlo to quantify parameter uncertainty and its effect on predictions of a groundwater flow model[J]. Environmental Moddelling & Software, 2009, 24(6):749-63. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a3ba178c48b0d63b420a771a6e1d6fd2 ROJAS R, KAHUNDE S, PETERS L, et al. Application of a multimodel approach to account for conceptual model and scenario uncertainties in groundwater modelling[J]. Journal of Hydrology, 2010, 394(3):416-35. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7b3427f235876bd3c2cda5424e4a8601 BLASONE R S, VRUGT J A, MADSEN H, et al. Generalized likelihood uncertainty estimation(GLUE) using adaptive Markov Chain Monte Carlo sampling[J]. Advances in Water Resources, 2008, 31(4):630-48. doi: 10.1016/j.advwatres.2007.12.003 KUCZERA G, PARENT E. Monte Carlo assessment of parameter uncertainty in conceptual catchment models:the metropolis algorithm[J]. Journal of Hydrology, 1998, 211(1):69-85. doi: 10.1016-S0022-1694(98)00198-X/ ROJAS R, FEYEN L, BATCLAAN O, et al. On the value of conditioning data to reduce conceptual model uncertainty in groundwater modeling[J]. Water Resources Research, 2010, 46:W08520-1-W08520-75. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=e1552687227b55f831858d44c13751d7 刑贞相, 芮孝芳, 崔海燕, 等.基于AM-MCMC算法的贝叶斯概率洪水预报模型[J].水利学报, 2007, 38(12):1500-1506. doi: 10.3321/j.issn:0559-9350.2007.12.014XING Zhenxiang, RUI Xiaofang, CUI Haiyan, et al. Bayesian probabilistic flood forecasting model based on adaptive metropolis-MCMC algorithm[J]. Journal of Hydraulic Engineering, 2007, 38(12):1500-1506. doi: 10.3321/j.issn:0559-9350.2007.12.014 ROJAS R, FEYEN L, DASSARGUES A. Conceptual model uncertainty in groundwater modeling:Combining generalized likelihood uncertainty estimation and Bayesian model averaging[J]. Water Resources Research, 2008, 44:12418. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ027477747/ NEUMAN S P. Maximum likelihood Bayesian averaging of uncertain model predictions[J]. Stochastic Environmental Research and Risk Assessment, 2003, 17(5):291-305. doi: 10.1007/s00477-003-0151-7 YE M, NEUMAN S P, MEYER P D. Maximum likelihood Bayesian averaging of spatial variability models in unsaturated fractured tuff[J]. Water Resources Research, 2004, 40:W05113-1-W05113-21. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=4eb4da517a2a77101e0cbc15f40c48de 曾献奎, 王栋, 吴吉春.地下水流概念模型的不确定性分析[J].南京大学学报:自然科学, 2012, 48(6):746-752. http://d.old.wanfangdata.com.cn/Periodical/njdxxb201206008ZENG Xiankui, WANG Dong, WU Jichun. Uncertainty analysis of groundwater flow conceptual model[J]. Journal of Nanjing University:Natural Sciences, 2012, 48(6):746-753. http://d.old.wanfangdata.com.cn/Periodical/njdxxb201206008 NEUMAN S P. Maximum likelihood Bayesian averaging of alternative conceptual mathematical models[J]. Stochastic Environmental Research and Risk Assessment, 2003, 17(5):291-305. doi: 10.1007/s00477-003-0151-7 REFSGAARD J C, SLUIJS J P V D, BROWN J, et al. A framework for dealing with uncertainty due to model structure error[J]. Advances in Water Resources, 2006, 29:1586-1597. doi: 10.1016/j.advwatres.2005.11.013 GILKS W R, RICHARDSON S, SPIEGELHALTER D J. Markov chain monte carlo in practice[M]. London:Chapman & Hall, 1996:112-119. HAARIO H, SAKSMAN E, TAMMINEN J. An adaptive metropolis algorithm[J]. Bernoulli, 2001, 7(2):223-242. doi: 10.2307/3318737 HAARIO H, SAKSMAN E, TANMIINEN J. Componentwise adaptation for high dimensional MCMC[J]. Computational Statistics, 2005, 20(2):265-273. doi: 10.1007/BF02789703 GEHNAN A, CARLIN J B, STREN H.S, et al. Bayesian data analysis[M]. London:Chapmann and Hall, 1995:142-151. BURNHAM K P, ANDERSON D R. Model selection and multi-model inference:a practical information-theoretic approach[M]. New York:Springer-Verlag, 2002:163-177. POETER E P, ANDERSON D. Multi-model ranking and inference in groundwater modeling[J]. Ground Water, 2005, 43(4):597-605. 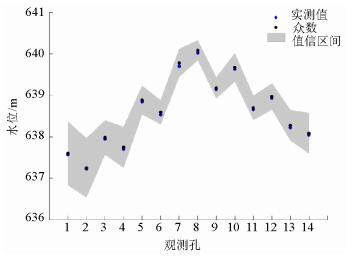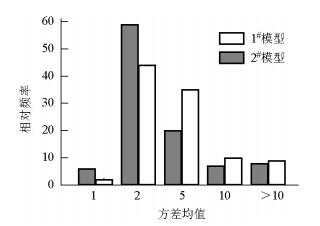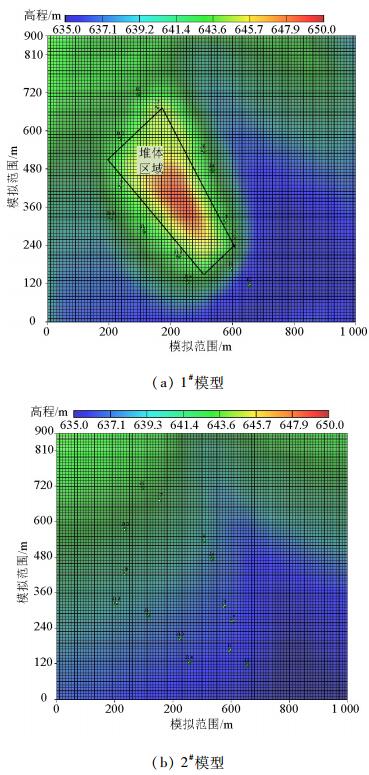doi: 10.1111/gwat.2005.43.issue-4 夏强.地下水不确定性问题的多模型分析方法及应用[D].北京: 中国地质大学, 2011. 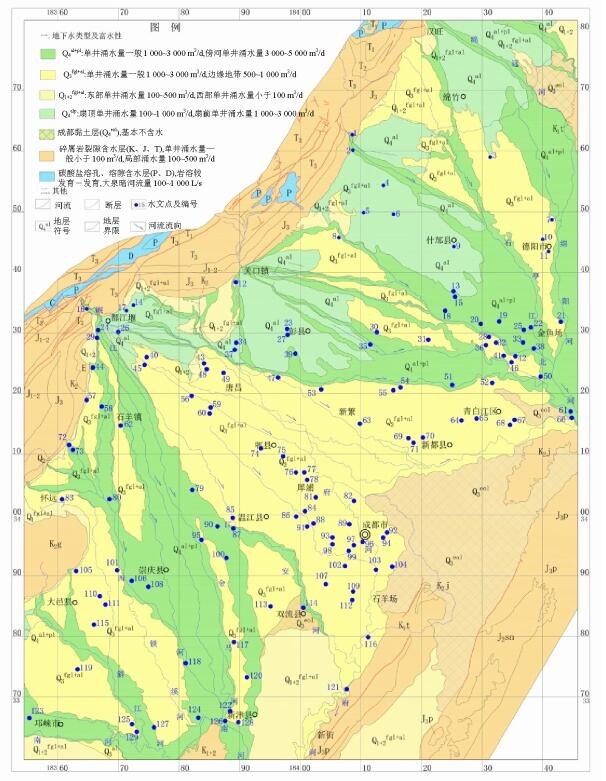http://cdmd.cnki.com.cn/Article/CDMD-11415-1011077537.htm 四川省地质局.成都幅水文地质报告[R].成都: 四川省地质局, 1977. 四川省地质局.都江堰幅水文地质报告[R].成都: 四川省地质局, 1977. 四川省地质矿产局.成都平原水文地质工程地质综合勘察评价报告[R].成都: 四川省地质矿产局, 1985. -
下载:
点击查看大图
图(5)
计量
- 文章访问数: 408
- HTML全文浏览量: 176
- PDF下载量: 71
- 被引次数: 0