颤振临界风速计算值与试验值的一致性

伍波; 王骑; 李志国; 廖海黎

doi:10.3969/j.issn.0258-2724.2018.03.012

颤振临界风速计算值与试验值的一致性

doi: 10.3969/j.issn.0258-2724.2018.03.012

伍波^1,2,,
王骑^1,2, ,,
李志国^1,2,
廖海黎^1,2

基金项目:

国家自然科学基金资助项目 51678508

国家自然科学基金资助项目 51308478

国家973计划资助项目 2013CB036301

详细信息

作者简介:
伍波(1989-), 男, 博士研究生, 研究方向为大跨度桥梁抗风研究, E-mail:wubo243@my.swjtu.edu.cn

通讯作者:
王骑(1980-), 男, 副教授, 博士, 硕导, 研究方向为大跨度桥梁抗风和钝体空气动力学, E-mail:wangchee_wind@swjtu.edu.cn

中图分类号: U448.43
计量
- 文章访问数: 601
- HTML全文浏览量: 227
- PDF下载量: 81
- 被引次数: 0
出版历程
- 收稿日期: 2017-06-26
- 刊出日期: 2018-06-25

Consistency between Calculated and Tested Values of Critical Flutter Speed of Flat Box Girder

WU Bo^{1,2
,},
WANG Qi^{1,2
, ,},
LI Zhiguo^1,2,
LIAO Haili^1,2

摘要

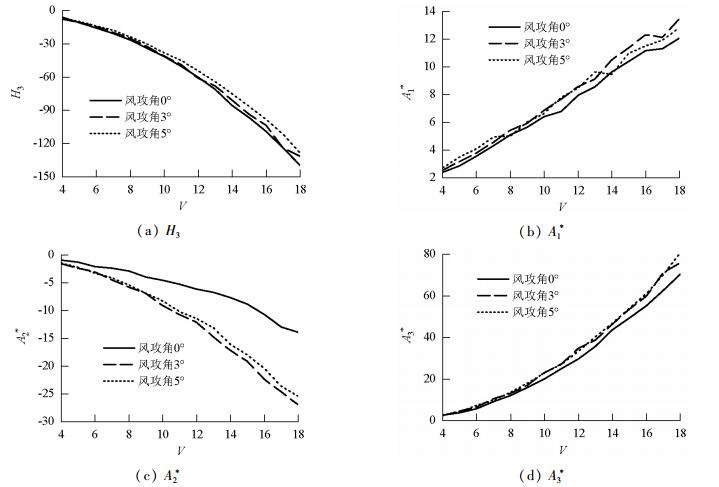
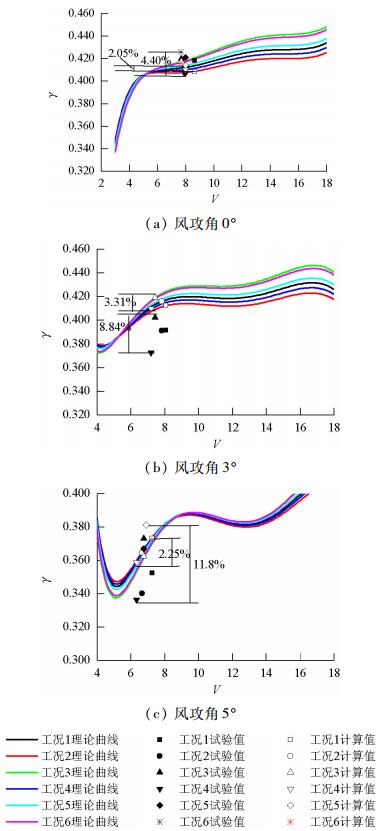
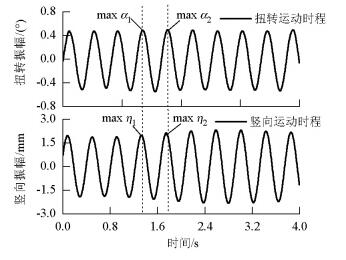
摘要: 为了准确把握扁平箱梁的颤振性能，采用节段模型风洞试验和颤振计算相结合的方法，研究了扁平箱梁断面在不同风攻角下颤振临界风速计算值与试验值的一致性.首先通过强迫振动风洞试验获得了某箱梁断面模型颤振导数；然后通过耦合颤振闭合解法获得了不同动力参数条件下的颤振临界风速；最后通过弹簧悬挂节段模型风洞试验测试获得了相同参数条件下的颤振临界风速.计算值和试验值对比结果表明：在0°攻角下扁平箱梁模型颤振临界风速的计算值与试验值保持一致，6种工况下两者差异分别为0.12%、0.50%、4.90%、4.10%、4.84%和1.43%；当风攻角为3°和5°时，颤振临界风速的计算值与试验值较难保持一致，最大差异值可到10.4%；通过对比颤振因子在计算和试验条件下的离散性，在排除非线性气动力和结构阻尼的影响后，推测造成此差异的原因是耦合颤振运动中相位角的变化引起了颤振导数的变化.
- 扁平箱梁 /
- 颤振临界风速 /
- 颤振导数 /
- 风攻角 /
- 一致性
Abstract: To obtain the precise flutter performance of a flat box girder, concordances between calculated values and tested values of critical flutter speed were studied, using sectional model wind tunnel testing combined with the calculation method of critical flutter speed. The flutter derivatives under different wind attacks of the box girder were obtained using forced vibration tests. The critical flutter speeds were then calculated using the bimodal coupled flutter analysis method. Finally, the critical flutter velocities were obtained via the sectional model tests under the same conditions. The results indicate that the differences between calculated and tested critical speeds in all cases are minor, and the percent errors are less than 5% when the attack angle is 0°. The differences between calculated and tested critical speeds are substantial when the attack angles are 3° and 5°, and the percent error can reach 10.4%. Based on a comparison of flutter factors derived from the calculation and the test, excluding the effect of nonlinear aerodynamic force and structural damping, it is conjectured that the differences may have been induced by variation in flutter derivatives caused by different coupled motions.
- flat box girder /
- critical flutter speed /
- attack angles /
- wind tunnel test /
- consistency

HTML全文

图 1 试验模型断面

Figure 1. Cross-Section of model

下载: 全尺寸图片幻灯片

图 2 强迫振动风洞试验

Figure 2. Forced vibration testing for section model

下载: 全尺寸图片幻灯片

图 3 试验断面不同攻角下4个关键颤振导数的测试结果

Figure 3. Flutter derivatives of the girder under different angle of attacks

下载: 全尺寸图片幻灯片

图 4 颤振因子试验值与计算值对比

Figure 4. Comparison of RC of flutter factors

下载: 全尺寸图片幻灯片

图 5 颤振响应时程图

Figure 5. Time-history response of flutter

下载: 全尺寸图片幻灯片

图 6 颤振因子及相位差关系图

Figure 6. Comparison of flutter factor and phase difference

下载: 全尺寸图片幻灯片

表 1 颤振性能计算及测试工况

Table 1. Calculating and testing cases for flutter

工况	M	I_m	r/b	f_h	f_t	ξ_s1	ξ_s2	η
1	22.12	0.685	0.518	1.63	3.00	0.470	0.253	0.54
2	20.14	0.681	0.541	1.75	3.06	0.485	0.287	0.57
3	22.12	0.780	0.552	1.63	2.81	0.476	0.298	0.58
4	20.14	0.755	0.569	1.75	2.94	0.456	0.312	0.60
5	20.14	0.861	0.608	1.75	2.75	0.462	0.265	0.63
6	22.12	0.987	0.621	1.63	2.50	0.476	0.304	0.65
注: f_h、f_t分别为系统竖向频率及扭转频率, Hz; M、I_m分别为系统总质量及质量惯性矩, kg、kg·m²; ξ_s1为系统竖向阻尼比, %; η为系统的弯扭频率比.

下载: 导出CSV

表 2 颤振临界风速试验值与计算值的对比

Table 2. Comparison of calculated results and tested results of critical flutter speed

攻角/(°)	工况	r/b	f_t	f_t/f_h	测试结果	计算结果	误差/%
0	1	0.518	3.00	1.85	8.62	8.63	0.12
	2	0.541	3.06	1.77	7.99	7.95	-0.50
	3	0.552	2.81	1.73	7.96	8.35	4.90
	4	0.569	2.94	1.68	7.99	7.66	-4.10
	5	0.608	2.75	1.57	7.65	7.27	-4.84
	6	0.621	2.50	1.54	7.69	7.58	-1.43
3	1	0.518	3.00	1.85	8.08	8.58	6.20
	2	0.541	3.06	1.77	7.20	7.50	4.00
	3	0.552	2.81	1.73	7.83	7.85	0.26
	4	0.569	2.94	1.68	7.45	7.20	-3.40
	5	0.608	2.75	1.57	7.36	6.80	7.70
	6	0.621	2.50	1.54	7.44	7.10	-4.60
5	1	0.518	3.00	1.85	7.24	6.84	5.40
	2	0.541	3.06	1.77	6.31	6.71	6.66
	3	0.552	2.81	1.73	6.65	6.52	-1.90
	4	0.569	2.94	1.68	6.74	6.11	-9.30
	5	0.608	2.75	1.57	6.89	6.26	-9.10
	6	0.621	2.50	1.54	6.75	6.05	-10.40

下载: 导出CSV

表 3 颤振因子计算值与试验反算值对比

Table 3. Comparison of calculated results and tested results

攻角/(°)	工况	γ_s	C₂/%	γ	C₁/%
0	1	0.418	1.9	0.409	2.05
	2	0.412	3.3	0.410	1.70
	3	0.407	4.5	0.412	1.21
	4	0.421	1.2	0.414	0.77
	5	0.426	0	0.416	0.27
	6	0.420	1.4	0.417	0
3	1	0.391	4.4	0.412	1.52
	2	0.373	8.8	0.409	2.18
	3	0.391	4.4	0.416	0.70
	4	0.392	4.2	0.415	0.94
	5	0.409	0	0.418	1.96
	6	0.402	1.7	0.419	0
5	1	0.353	7.3	0.373	2.24
	2	0.336	11.8	0.359	1.69
	3	0.340	10.8	0.365	0
	4	0.367	3.4	0.364	0.09
	5	0.381	0	0.365	0
	6	0.373	2.1	0.362	0.74

下载: 导出CSV

表 4 不同结构阻尼比下颤振临界风速计算结果

Table 4. Critical velocities under different damping ratios

m/s
工况	0.2%	0.3%	0.4%	0.5%	最大改变度/%
1	6.8	6.86	6.90	6.93	1.9
2	6.66	6.72	6.76	6.82	2.4
3	6.45	6.52	6.59	6.65	3.1
4	6.00	6.10	6.13	6.19	3.2
5	6.21	6.28	6.35	6.41	3.2
6	5.99	6.05	6.12	6.19	3.3

下载: 导出CSV

表 5 不同结构阻尼比下颤振因子计算结果

Table 5. Flutter factors under different damping ratios

工况	0.2%	0.3%	0.4%	0.5%	C₂/%
1	0.331	0.334	0.336	0.337	1.8
2	0.355	0.358	0.360	0.363	2.3
3	0.330	0.333	0.337	0.340	3.0
4	0.328	0.332	0.334	0.337	2.7
5	0.344	0.347	0.351	0.355	3.2
6	0.331	0.334	0.338	0.342	3.3

下载: 导出CSV

参考文献(17)

WILDE K, FUJINO Y, MASUKAWA J. Time domain modeling of bridge deck[J]. Structural Engineering Earthquake Engineering, 2010, 13(2):93-104

MASUMOTO M. Aerodynamic damping of prisms[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 59(2/3):159-175. http://www.sciencedirect.com/science/article/pii/0167610596000050

CHEN X, MASUMOTO M, KAREEM A. Time domain flutter and buffeting response analysis of bridges[J]. Journal of Engineering Mechanics, 2000, 126(1):7-16. doi: 10.1061/(ASCE)0733-9399(2000)126:1(7)

CHEN X. Improved understanding of bimodal coupled bridge flutter based on closed-form solution[J]. Journal of Engineering Mechanics, 2007, 133(1):22-31. doi: 10.1061/(ASCE)0733-9399(2007)133:1(22)

SCANLAN R, TOMKO J. Airfoil and bridge deck flutter derivatives[J]. Journal of Engineering Mechanics, 1971, 97:1717-1737. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JAKO200421349898472

SARKAR P P, JONES N P, SCANLAn R H. Identification of aeroelastic parameters of flexible bridges[J]. Journal of Engineering Mechanics, 1994, 120(8):1718-1742. doi: 10.1061/(ASCE)0733-9399(1994)120:8(1718)

MATSUMOTO M, NIIHARA Y, KOBAYASHI Y, et al. Flutter mechanism and stabilization of bluff bodies[C]//Proceedings of the Ninth ICWE. New Delhi: Wiley Eastern Limited, 1995: 827-838.

CHEN X, KAREEM A. Efficacy of the implied approximation in the identification of flutter derivatives[J]. Journal of Engineering Mechanics, 2004, 130(12):2070-2074. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=59109bff8b4df9e890cf2713e530a2e2

ARGENTINI T, DIANA G, ROCCHI D, et al. A case-study of double multi-modal bridge flutter:Experimental result and numerical analysis[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2016, 151:25-36. http://www.sciencedirect.com/science/article/pii/S0167610516000143

丁泉顺.大跨度桥梁耦合颤抖振响应的精细化分析[D].上海: 同济大学, 2001. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y401445

GE Y J, XIANG H F. Computational models and methods for aerodynamic flutter of long-span bridges[J]. China Civil Engineering Journal, 2008, 96(10/11):1912-1924. http://www.sciencedirect.com/science/article/pii/S0167610508000639

王骑, 廖海黎, 李明水, 等.大振幅下薄翼和流线型箱梁的气动迟滞研究[J].实验流体力学, 2013, 27(1):32-37. doi: 10.3969/j.issn.1672-9897.2013.01.006

WANG Qi, LIAO Haili, LI Mingshui, et al. Aerodynamic hysteresis of thin airfoil and streamline box girder under large amplitude oscillation[J]. Journal of Experiment in Fluid Mechanics, 2013, 27(1):32-37. doi: 10.3969/j.issn.1672-9897.2013.01.006

WANG Qi, LIAO Haili, LI Mingshui, et al. Coupling and nonlinearity and span-wise correlation in aerodynamic force of a rectangular cylinder[C]//The 8th International Colloquium on Bluff Body Aerodynamics and Applications. Boston: [s.n.], 2016: 1-8.

NODA M, UTSUNOMIYA H, NAGAO F, et al. Effects of oscillation amplitude on aerodynamic derivatives[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(1):101-11. http://www.sciencedirect.com/science/article/pii/S0167610502003380

MASUMOTO M, SHIRAISHI N, SHIRATO H, et al. Aerodynamic derivatives of coupled/hybrid flutter of fundamental structural sections[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49(1/2/3):575-584. http://www.sciencedirect.com/science/article/pii/016761059390051O

LEE T, SU Y Y. Surface pressures developed on an airfoil undergoing heaving and pitching motion[J]. Journal of Fluids Engineering, 2015, 137(5):051105. doi: 10.1115/1.4029443

LIAO H, WAN J W, WANG Q, et al. Numerical study on nonlinear and motion coupling effects on self-excited force of a bridge deck[C]//The 8th International Colloquium on Bluff Body Aerodynamics and Applications. Boston: [s.n.], 2016: 1-8.

施引文献

附加材料(0)

访问统计