基于EEMD-TEO熵的高速列车轴承故障诊断方法

靳行; 林建辉; 伍川辉; 邓韬; 黄晨光

doi:10.3969/j.issn.0258-2724.2018.02.019

基于EEMD-TEO熵的高速列车轴承故障诊断方法

doi: 10.3969/j.issn.0258-2724.2018.02.019

基金项目:

四川省科技支撑计划资助项目 2016JY0047

详细信息

作者简介:
靳行(1986-), 男, 博士研究生, 研究方向为信号处理与机械故障诊断, E-mail:wzem007@gmail.com

通讯作者:
林建辉(1964-), 男, 教授, 博士, 研究方向为信号处理与机械故障诊断, E-mail:linjhyz@sina.com

中图分类号: U279.3
计量
- 文章访问数: 470
- HTML全文浏览量: 247
- PDF下载量: 209
- 被引次数: 0
出版历程
- 收稿日期: 2016-04-07
- 刊出日期: 2018-04-25

Diagnostic Method for High-Speed Train Bearing Fault Based on EEMD-TEO Entropy

摘要

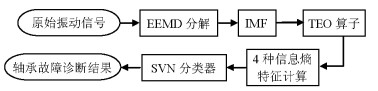
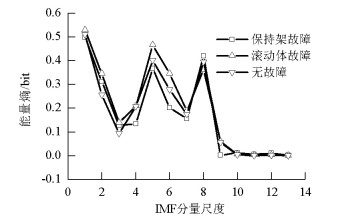
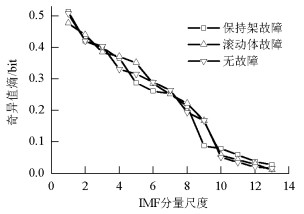
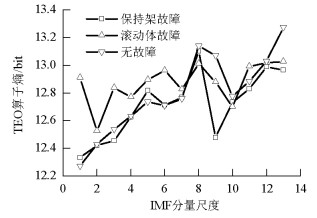
摘要: 为了解决高速列车轴承早期故障中低频信号的类间分离性较弱、保持架故障难以识别等的问题，提出了基于Teager能量算子（Teager energy operator，TEO）聚合经验模态分解（ensemble empirical mode decomposition，EEMD）熵的自适应诊断方法.该方法将EEMD、样本熵、TEO相结合，利用EEMD的自适应性得到固有模态（intrinic mode function，IMF）信号，用改进的TEO从IMF中提取得到样本熵，使用支持向量机（support vector machine，SVM）判断轴承工作状态与故障类型；讨论了EEMD能量熵、EEMD奇异值熵、EEMD-TEO时频熵生成的故障特征向量以及该向量在SVM中识别结果；对正常轴承、保持架故障、滚动体故障3种状态的轴承样本数据进行了故障诊断.研究结果表明：对3种轴承的故障识别率可以达到98%，较传统的经验模态熵识别率提高了2.6%，该方法可用作高速列车轴承状态诊断.
- 经验模态分解 /
- 奇异值分解 /
- Teager能量算子 /
- 瞬时频率 /
- 轴承故障
Abstract: To overcome the limitations of the between-class separateness of low-frequency signals of high-speed train bearing faults as well as the problem of fault identification of the cage, an adaptive diagnostic method based on the Teager energy operator (TEO) and ensemble empirical mode decomposition (EEMD) entropy is proposed. This method combines the EEMD, sample entropy, and the TEO, and the intrinsic mode function (IMF) signal is obtained by the self-adaptation of EEMD, and then the sample entropy is obtained from the IMF using the improved TEO. Finally, the support vector machine (SVM) is used to determine the working state and fault type of the bearing. The fault eigenvectors of the EEMD energy entropy, EEMD singular value entropy, EEMD-TEO time-frequency entropy generation, and the identification results of this vector in the SVM are discussed. The method was used to diagnosethefault ofbearingsviathedata in three states:normal bearing, retainer bearing, and fault of the rolling body. The results show that the fault recognition rate for the three bearing states can reach 98%, increased by 2.6% compared to the traditional empirical mode entropy, this method can be used for the diagnosis of high-speed train bearings.
- empirical mode classification /
- singular value decomposition /
- Teager energy operator /
- singular value spectrum /
- bearing fault

HTML全文

图 1 EEMD分解流程

Figure 1. EEMD decomposition flow chart

下载: 全尺寸图片幻灯片

图 2 瞬时谱图

Figure 2. Improved TEO transient spectrum

下载: 全尺寸图片幻灯片

图 3 信号的处理流程

Figure 3. Signal processing flow

下载: 全尺寸图片幻灯片

图 4 试验现场

Figure 4. Test site map

下载: 全尺寸图片幻灯片

图 5 轴承的振动试验数据

Figure 5. Bearing vibration test data

下载: 全尺寸图片幻灯片

图 6 轴承的振动试验数据

Figure 6. Vibration data of bearing

下载: 全尺寸图片幻灯片

图 7 EEMD-TEO时频熵与改进的TEO熵盒图

Figure 7. EEMD-TEO time-frequency entropy and Improved TEO entropy box diagram

下载: 全尺寸图片幻灯片

图 8 EEMD能量谱熵的熵值分布

Figure 8. EEMD energy spectrum entropy distribution

下载: 全尺寸图片幻灯片

图 9 EEMD奇异熵的熵值分布

Figure 9. EEMD Singular entropy distribution

下载: 全尺寸图片幻灯片

图 10 TEO算子熵分布

Figure 10. TEO operator entropy distribution

下载: 全尺寸图片幻灯片

图 11 EEMD-TEO熵分布

Figure 11. EEMD-TEO time frequency entropy distribution

下载: 全尺寸图片幻灯片

图 12 改进TEO时频样本熵向量

Figure 12. Improved TEO time frequency sample entropy vector

下载: 全尺寸图片幻灯片

图 13 HHT时频熵向量

Figure 13. HHT time frequency entropy vector

下载: 全尺寸图片幻灯片

表 1 双列圆锥滚子轴承的主要参数

Table 1. Main parameters of double row tapered roller bearings

滚动体直径/mm	轴承节径 /mm	滚动体数量	压力角/rad
26.9	180	19	π/20

下载: 导出CSV

表 2 不同工况下的各种熵均值

Table 2. Various entropy values under different operating conditions

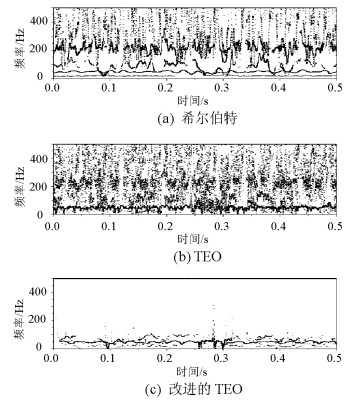
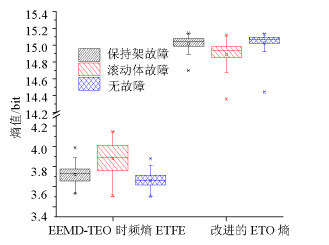
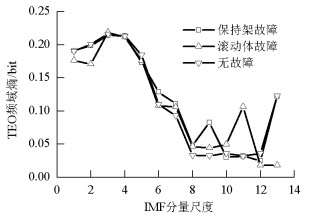
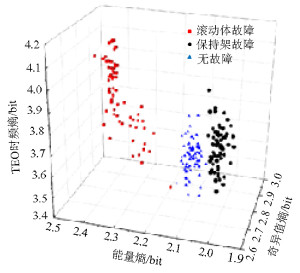
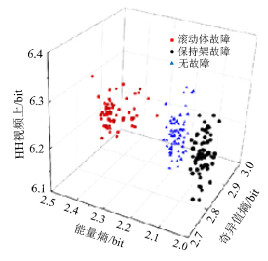
bit
工况	E_EEE	E_ESE	E_ETOE	E_ETTFE	HHT
无故障	2.10	2.75	14.95	3.66	6.28
保持架故障	2.01	2.77	14.94	3.72	6.24
滚动体故障	2.35	2.80	14.88	3.88	6.26

下载: 导出CSV

表 3 不同工况下熵值协方差

Table 3. Different conditions of entropy covariance

工况	EEMD-TEO	经验模态熵向量
无故障与保持架故障	0.029	0.016
无故障与滚动体故障	0.108	0.009
保持架故障与滚动体故障	0.079	0.007
总体方差	0.144	0.030

下载: 导出CSV

表 4 两种特征提取方法的识别率对比

Table 4. Comparison of recognition rates of two types of feature extraction methods

%
特征提取方法	正常轴承	保持架故障	滚动体故障
传统经验模态熵	95.30	92.30	98.46
EEMD-TEO熵	100.00	98.46	98.46

下载: 导出CSV

参考文献(17)

李熙.城市轨道交通车辆走行部安全评估方法研究[D].北京: 北京交通大学, 2011.

唐德尧.广义共振、共振解调故障诊断与安全工程:铁路篇[M].北京:中国铁道出版社, 2006:11-13.

胡爱军, 马万里, 唐贵基.基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J].中国电机工程学报, 2012, 32(11):106-111. http://d.old.wanfangdata.com.cn/Periodical/zgdjgcxb201211018

HU Aijun, MA Wanli, TANG Guiji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J]. Proceedings of the CSEE, 2012, 32(11):106-111. http://d.old.wanfangdata.com.cn/Periodical/zgdjgcxb201211018

陈志新, 徐金梧, 杨德斌.基于复小波块阈值的降噪方法及其在机械故障诊断中的应用[J].机械工程学报, 2007, 43(6):200-204. doi: 10.3321/j.issn:0577-6686.2007.06.036

CHEN Zhixin, XU Jinwu, YANG Debin. Denoising method of block thresholding based on DT-CWT and its application in mechanical fault diagnosis[J]. Chinese Journal of Mechanical Engineering, 2007, 43(6):200-204. doi: 10.3321/j.issn:0577-6686.2007.06.036

李富才, 何正嘉, 陈进.小波域相关滤波法及其早期故障预示应用[J].振动工程学报, 2005, 18(2):145-148. doi: 10.3969/j.issn.1004-4523.2005.02.003

LI Fucai, HE Zhengjia, CHEN Jin. Wavelet transform domain correlation filter and its application in incipient fault prognosis[J]. Journal of Vibration Engineering, 2005, 18(2):145-148. doi: 10.3969/j.issn.1004-4523.2005.02.003

PUBCYS S M. Approximate entropy as a complexity measure[J]. Chaos, 1995, 5(1):110-117. doi: 10.1063/1.166092

赵志宏, 杨绍普.一种基于样本熵的轴承故障诊断方法[J].振动与冲击, 2012, 31(6):136-140 doi: 10.3969/j.issn.1000-3835.2012.06.028

ZHAO Zhihong, YANG Shaopu. Sample entropy-based roller bearing fault diagnosis method[J]. Journal of Vibration and Shock, 2012, 31(6):136-140. doi: 10.3969/j.issn.1000-3835.2012.06.028

TANELLI M, PIRODDI L, SAVARESI S M. Real-time identification of tier-road friction conditions[J]. IET Control Theory Applications, 2009, 3(7):891-906. doi: 10.1049/iet-cta.2008.0287

HE Zhengyou, CHEN Xiaoqing, LUO Guoming. Wavelet entropy measure definition and its application for transmission line fault detection and identification; (part Ⅰ: definition and methodology)[C]//Power System Technology, 2006. International Conference on Power System Technology.[S.l.]: IEEE, 2006, 82(10): 1-6.

秦娜, 王开云, 金炜东, 等.高速列车转向架故障的经验模态熵特征分析[J].交通运输工程学报, 2014, 14(1):57-64, 74. doi: 10.3969/j.issn.1671-1637.2014.01.010

QIN Na, WANG Kaiyun, JIN Weidong, et al. Fault feature analysis of high-speed train bogie based on empirical mode decomposition entropy[J]. Journal of Traffic and Transportation Engineering, 2014, 14(1):57-64, 74. doi: 10.3969/j.issn.1671-1637.2014.01.010

孙晖.经验模态分解理论与应用研究[D].杭州: 浙江大学, 2005.

WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[R]. Calcerton: Center for Ocean-Land-Atmosphere Studies, 2009.

丁建明, 王晗, 林建辉, 等.基于EMD-Hankel-SVD的高速列车万向轴动不平衡检测[J].振动与冲击, 2015, 34(9):164-170. http://d.old.wanfangdata.com.cn/Periodical/zdycj201509031

DING Jianming, WANG Han, LIN Jianhui, et al. Detection of dynamic imbalance due to cardan shaft in high-speed train based on EMD-Hankel-SVD method[J]. Journal of Vibration and Shock, 2015, 34(9):164-170. http://d.old.wanfangdata.com.cn/Periodical/zdycj201509031

RANDALL R B, ANTONI J. Rolling element bearing diagnostics-a tutorial[J]. Mechanical Systems and Signal Processing, 2011, 25(2):485-520. doi: 10.1016/j.ymssp.2010.07.017

Linkin.斯坦福大学机器学习——交叉验证(cross validation)[EB/OL].[2017-07-04].http://blog.csdn.net/linkin1005/article/details/42869331.

YI C, LIN J, RUAN T, et al. Real time cardan shaft state estimation of high-speed train based on ensemble empirical mode decomposition[J]. Shock and Vibration, 2015(4):1-12. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=Doaj000004035866

易彩.高速列车轮对轴承状态表征与故障诊断方法研究[D].成都: 西南交通大学, 2015.

施引文献

附加材料(0)

访问统计