Face Stability Analysis of Shield Tunnel in Sandy Ground Using 3D DEM
-
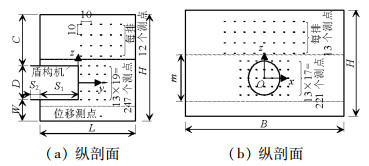
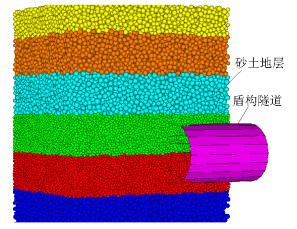
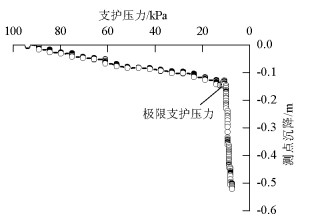
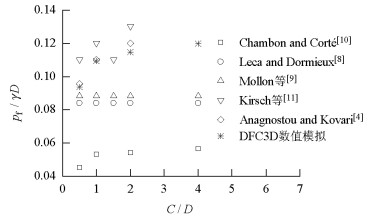
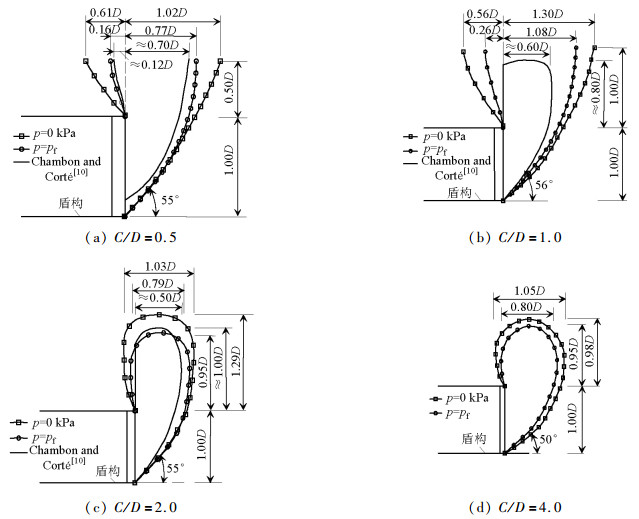
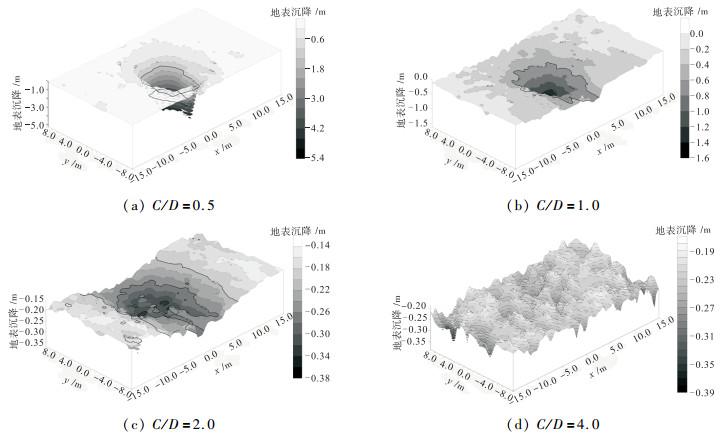
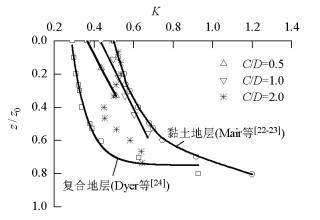
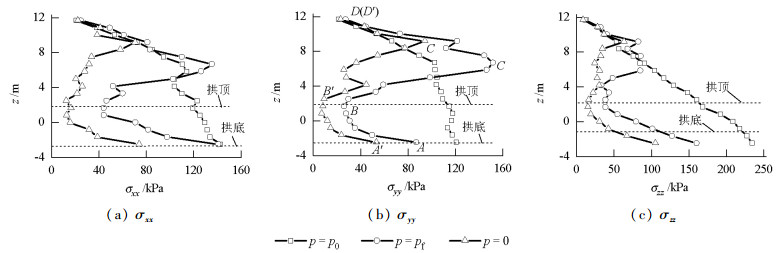
摘要: 为探明砂土地层盾构隧道掌子面的稳定性，以Chambon和Corté开展的模型试验为基础，采用三维离散元方法研究了隧道埋深对隧道掌子面稳定性的影响规律，并从细观角度解释了开挖面失稳机理.离散元模型引入了三维柔性应力边界，将模型试验中空气或流体压力对掌子面的支撑效应抽象为作用在掌子面颗粒上的指定支护压力，逐步减少该压力，结合地层变形精确得到极限支护压力.通过删除进入隧道轮廓内的砂土颗粒模拟盾构开挖，以考虑该施工力学行为对掌子面稳定性的影响.研究结果表明：隧道埋深与隧道直径之比小于等于1.0时，掌子面极限支护压力随埋深增加而增加，此后趋于稳定，砂土地层中极限支护压力比随埋深增加而减少，地表沉降突增点对应的支护压力小于掌子面极限支护压力，失稳区直接发展到地表，工程中应同时关注地表沉降与仓内支护压力以保证开挖面稳定；隧道埋深与隧道直径之比大于等于2.0时拱顶上方形成了稳定的塌落拱，延伸高度分别约为0.7D（隧道直径）~1.3D与0.9D~2.3D.Abstract: Based on the model test carried out by Chambon and Corte, the three-dimensional discrete element method (3D DEM) was used to study the face stability of shallow shield tunnels in sand, and the face failure mechanism was investigated from microscopic perspectives. A three-dimensional flexible stress boundary was implemented in the numerical model, and the support provided by air or fluid in the chamber for a tunnel face was simplified as specified normal pressure acting on face particles. Pressure was decreased gradually to 0 kPa, and ground deformation was closely recorded. Thus, the limit support pressure could be determined naturally. The tunnel excavation process was incorporated by deleting the particles that flowed into the tunnel, and its effect on tunnel stability was considered. Results show that when C (tunnel buried depth)/D (tunnel diameter) ≤ 1.0, the limit support pressure first increases with buried depth and then tends to be constant. The ratio of the limit support pressure to the initial support pressure decreases with buried depth. The support pressure at which ground settlement accelerates abruptly is smaller than the limit support pressure. The failure zone directly propagates up to the ground surface. In engineering practice, attention should be paid to the ground surface settlement and limit support pressure to keep the tunnel face safe. When C/D ≥ 2.0, a stable soil arch exists above the tunnel crown and extends upwards to approximately 0.7D-1.3D and 0.9D-2.3D.
-
竖井是连接地表和地下空间的咽喉通道，在军事工程、隧道工程等领域有着重要应用. 竖井全断面掘进机作为深竖井机械破岩技术的关键装备，采用反重力方式排渣[1-2]. 基于无水环境下刀盘的聚渣、斗轮排渣需求，竖井掌子面设为“W”型，因此，刀盘采用类“W”型结构设计. 异型刀盘锥面角度要大于岩渣安息角，在重力作用下岩渣滑落至类“W”型掌子面的凹陷区域，进而通过排渣装置将岩渣排出掌子面. 为了保证异型刀盘上滚刀破岩后的竖井掌子面为“W”型，需要研究得到高效破岩的滚刀安装排布参数，解决类“W”型刀盘结构造成滚刀安装布局困难的问题，并为竖井全断面掘进机异型刀盘提供刀具布局优化方案，对提高竖井掘进效率和刀盘力学性能等都有着重要作用.
国外厂家已研制出竖井全断面掘进机，在某些竖井工程进行施工试验，但尚未实现大规模推广[3]，而国内对竖井掘进机的研制及施工处于起步阶段. 目前关于隧道水平开挖下平面刀盘的刀具破岩及布局研究较多，Kang等[4]基于锥面破岩实验平台和数值模拟相结合的方式研究不同刀间距下滚刀破岩效果；刘立鹏等[5]利用PFC软件研究双滚刀间距及入岩次序对破岩效果的影响；Zhang等[6]利用PFC3D软件研究TBM （tunnel boring machine）滚刀破碎软硬不均地层的破岩机理；Cho等[7-8]通过实验与仿真相结合的方式确定滚刀最优间距；宁向可等[9]通过搭建实验台和仿真相结合，研究盘面锥角、滚刀安装间距以及安装倾角对锥面滚刀破岩效率的影响；薛亚东等[10]利用MatDEM软件结合室内线性切割试验对不同刀间距以及贯入比的滚刀破岩机理进行研究；张蒙祺等[11]研究不同岩石强度及不同围压下平头滚刀及圆弧滚刀的破岩机理，得到圆弧滚刀适合在岩石强度更高和围压更大的地层中破岩.
综上所述，国内外学者主要通过模拟仿真及破岩试验的方法研究多种因素下水平掘进的盾构机/TBM的平面刀盘破岩机理及刀具受力，包括岩石强度、围压等地质参数，刀具刃形、刃宽等滚刀结构参数及刀间距、贯入度等滚刀安装参数，但缺少对竖井工程中垂直开挖下异型刀盘滚刀布局的破岩效果研究. 由于异型刀盘的特殊构型设计，目前尚不清楚“W”型掌子面凹陷区域处滚刀组排布对破岩效果的影响. 关于异形刀盘锥面上滚刀安装倾角对破岩效率的影响，尚未形成相关定论，难以确定合理的滚刀布局方案. 因此，本文以国内首个千米硬岩竖井全断面掘进机开挖工程为背景，研究“W”型掌子面凹陷区域处滚刀组布局的破岩效果，研究刀盘锥面上滚刀刀间距及安装倾角的破岩效率，基于破岩比能得到合理的滚刀安装参数，在考虑排渣结构空间布局的基础上利用粒子群算法优化异型刀盘的刀具布局方案.
1. 工程背景
1.1 工程地质条件
西鞍山铁矿竖井开挖工程是国内首个采用竖井全断面掘进机施工的千米硬岩竖井工程，开挖直径为8.1 m，其地层主要由千枚岩组成，勘探得到的地层参数如表1. 该工程只有2个主要含水层，即第四系孔隙含水层和基岩构造裂隙含水层岩组，第四系含水层只在沟谷地带有零星分布，大部分已被矿山开采剥离；根据勘察钻孔岩芯资料显示，基岩裂隙含水岩组未见有大的断裂构造，施工过程未见明显涌、漏水现象，所以千枚岩地层富水性为弱富水性. 因此，竖井全断面掘进机异型刀盘的滚刀破岩及出渣结构设计均不考虑地下水对岩石特性的影响[12-13].
表 1 各地层岩石力学参数Table 1. Rock mechanics parameters of each stratum深度/m 地层 承载力/kPa 抗压强度/MPa 内摩擦角/（°） 凝聚力/MPa 密度/（g·cm−3） 2～4 粉质黏土 150 0.16 23.9 0.04 1.95 16～37 强风化石英岩 600 48.50 38.2 1.30 2.70 48～50 中风化石英岩 2500 63.50 5.2 4.50 2.90 60～79 微风化石英岩 5000 87.10 34.8 5.20 2.90 90～702 千枚岩 3500 78.50 24.8 9.93 2.70 1.2 竖井全断面掘进机异型刀盘
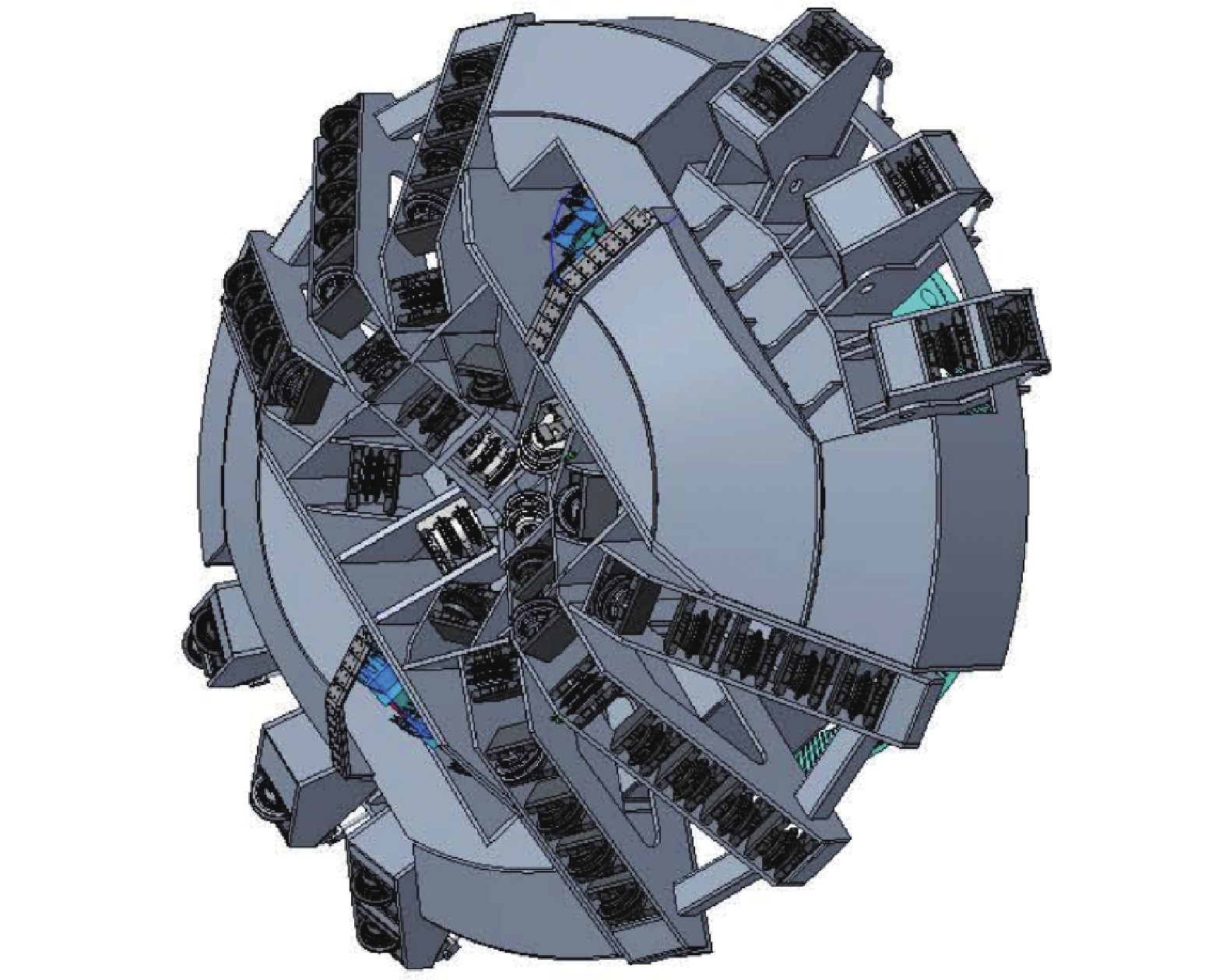
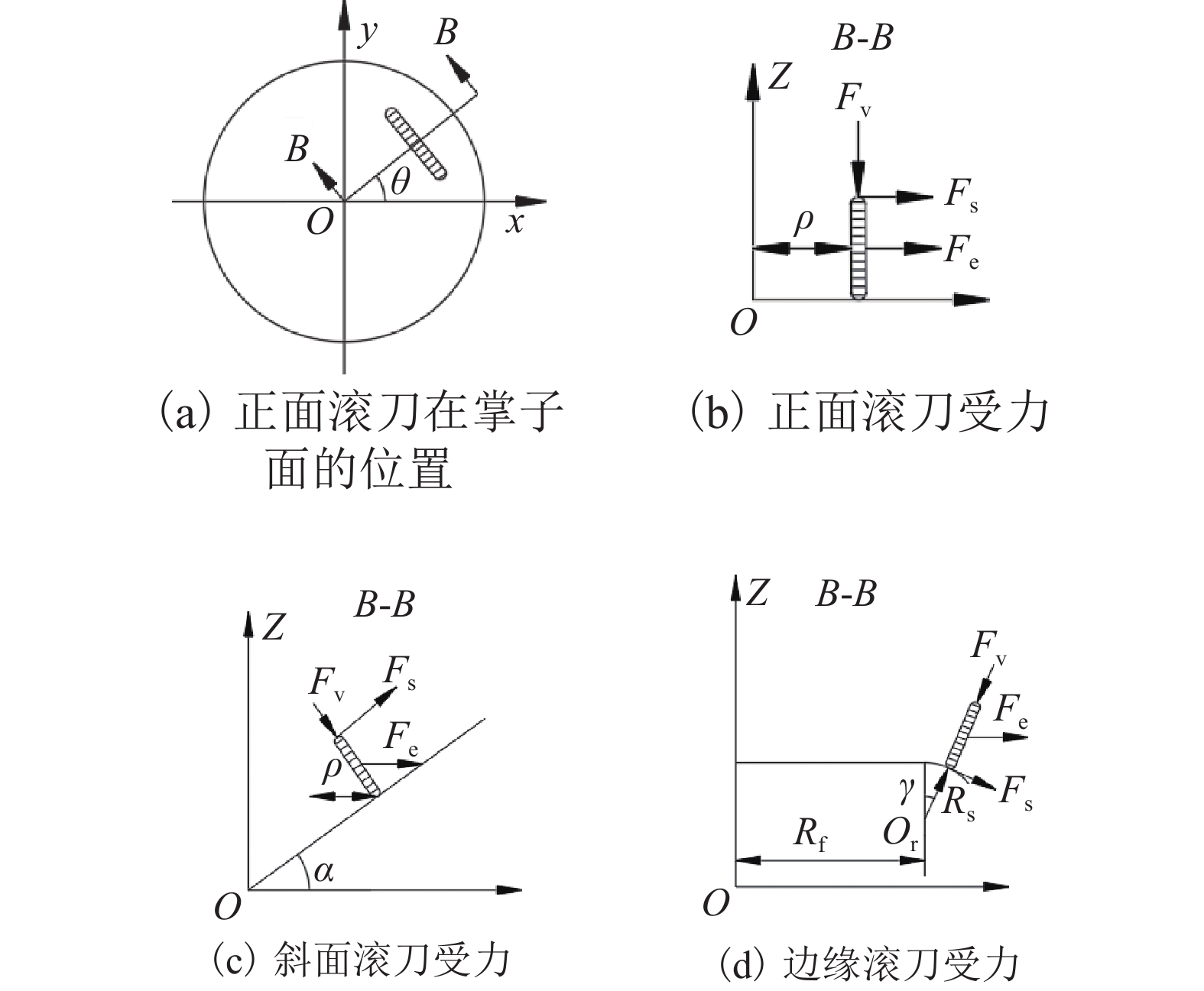
竖井全断面掘进机异型刀盘三维模型如图1所示，异型刀盘采用类“W”型设计. 由于岩渣的自然安息角一般为25°～30°[14]，为使岩渣在重力作用下滑落至凹陷区域处，将刀盘锥面角度设置为35°. 异型刀盘可划分为刀盘中心、掌子面凹陷区域、刀盘锥面三部分，滚刀按受力特点可划分为正滚刀、锥面滚刀和边缘滚刀[15]，如图2所示. 图中：Fv为垂直力，Fs为侧向力，Fe为惯性力的合力，ρ为滚刀到刀盘中心的距离，θ为滚刀位置的极角，α为锥面与水平面夹角，γ为边缘滚刀安装角度，Rs为刀盘边缘过渡圆弧的半径，Or为刀盘边缘过渡圆弧的圆心，Rf为刀盘边缘过渡圆弧圆心到刀盘中心的距离. 为了适应硬岩地层的破岩及耐磨要求，采用17 in盘形滚刀，滚刀刃宽20 mm，刃倾角20°. 滚刀破岩时其刀间距S设置与岩石破碎角β密切相关，可通过式（1）求得[16].
S=2htanβ2， (1) 式中：h为贯入度，mm.
设滚刀贯入度为15 mm，千枚岩破碎角约为145°，代入式（1）中，求得S=95 mm，因此，按设计经验刀间距取整后设为90 mm.
目前尚不清楚锥面上哪种滚刀安装方式的破岩效果最佳，包括滚刀垂直安装方式、竖向安装方式或一定安装倾角方式，只能参考平面刀盘上常用的滚刀垂直岩面安装方式，设滚刀安装倾角为0°，即滚刀垂直安装在“W”型刀盘上.
2. 异型刀盘结构下滚刀破岩效果
2.1 滚刀破岩仿真模型的建立
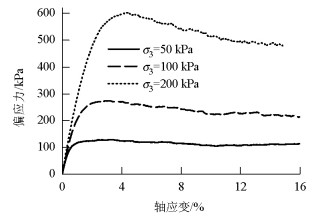
在离散元法仿真中，为保证所建立岩石模型与实际研究对象的宏观力学性质一致，需要对颗粒的细观参数进行参数标定. 单轴压缩试验、巴西劈裂试验是岩石的常用参数标定方法[17-18]. 采集千米硬岩竖井工程的千枚岩岩样，通过室内单轴压缩试验和巴西劈裂试验得到千枚岩的宏观物理力学参数和岩样破坏形式（图3）. 在千枚岩地层仿真模拟中，建立单轴压缩试验、巴西劈裂试验的仿真模型，经过多次细观参数数值标定试验，反复调整颗粒流模型的细观参数，得到了与实际岩石物理力学参数相匹配的颗粒流模型细观参数. 标定的千枚岩地层岩石细观参数如表2，应力-应变全过程曲线如图3所示[4].
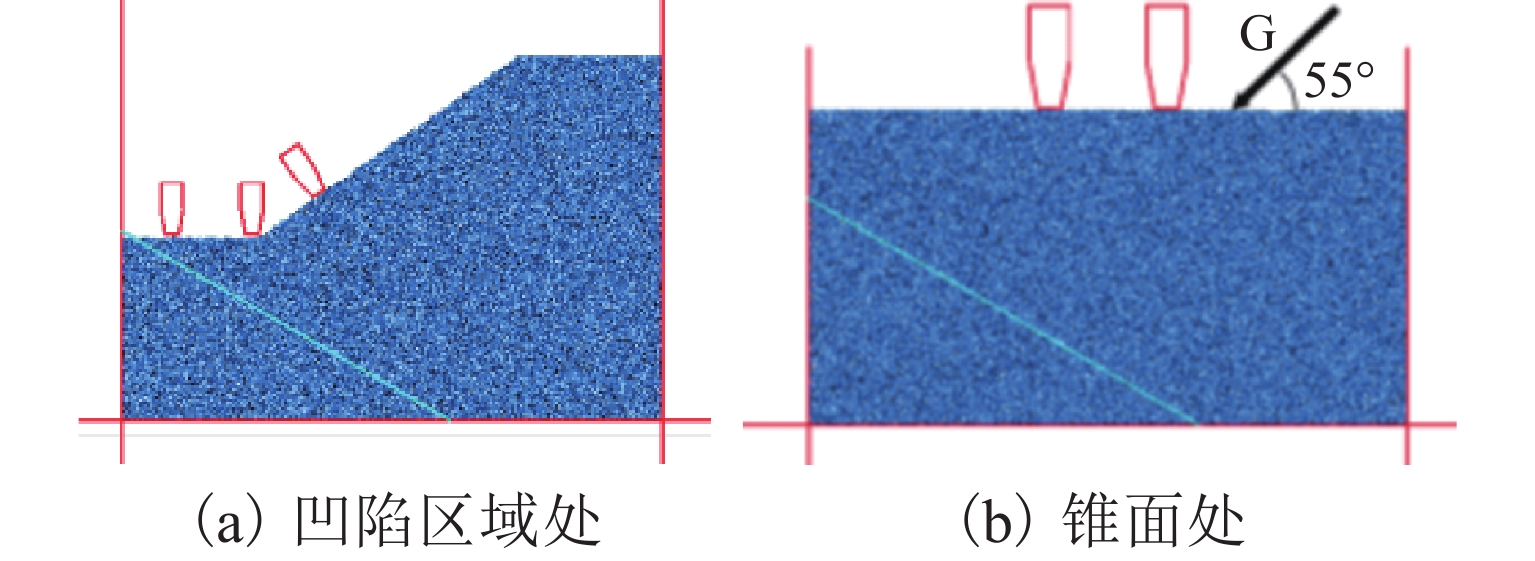
表 2 千枚岩体模型的细观参数Table 2. Meso-parameters of phyllite model参数 取值 有效模量/GPa 9.95 刚度比 1.5 胶结有效模量/GPa 9.95 胶结刚度比 1.5 内聚力/MPa 8.0 摩擦角/（°） 38.5 摩擦系数 0.6 本文采用PFC2D软件研究异型刀盘滚刀破岩效果. 其中，掌子面凹陷区域处滚刀破岩仿真，按照刀盘上安装布局的滚刀情况，建立3把滚刀协同破岩模型，如图4（a）. 进行刀盘锥面上滚刀不同刀间距及安装倾角的破岩仿真时，为加快离散元仿真建模及运行速度，通过设置重力G方向与水平的夹角为55°，将35° 的锥面岩石模型设置为水平岩石模型，以此模拟刀盘锥面上滚刀协同破岩，如图4（b）. 岩石模型长度为400 mm，高度为200 mm，节理倾角为30°，节理间距为35 mm[19]. 颗粒细观参数由表2确定. 由于滚刀其余结构在破岩过程中与岩石无直接作用，所以只需利用刚性墙体模拟盘形滚刀刀圈结构. 给刀圈施加恒定的下压速度，模拟刀盘掘进运动过程，利用hist函数监测刀圈所受的载荷以及岩石破碎体积等参数.
2.2 凹陷区域处滚刀破岩效果研究
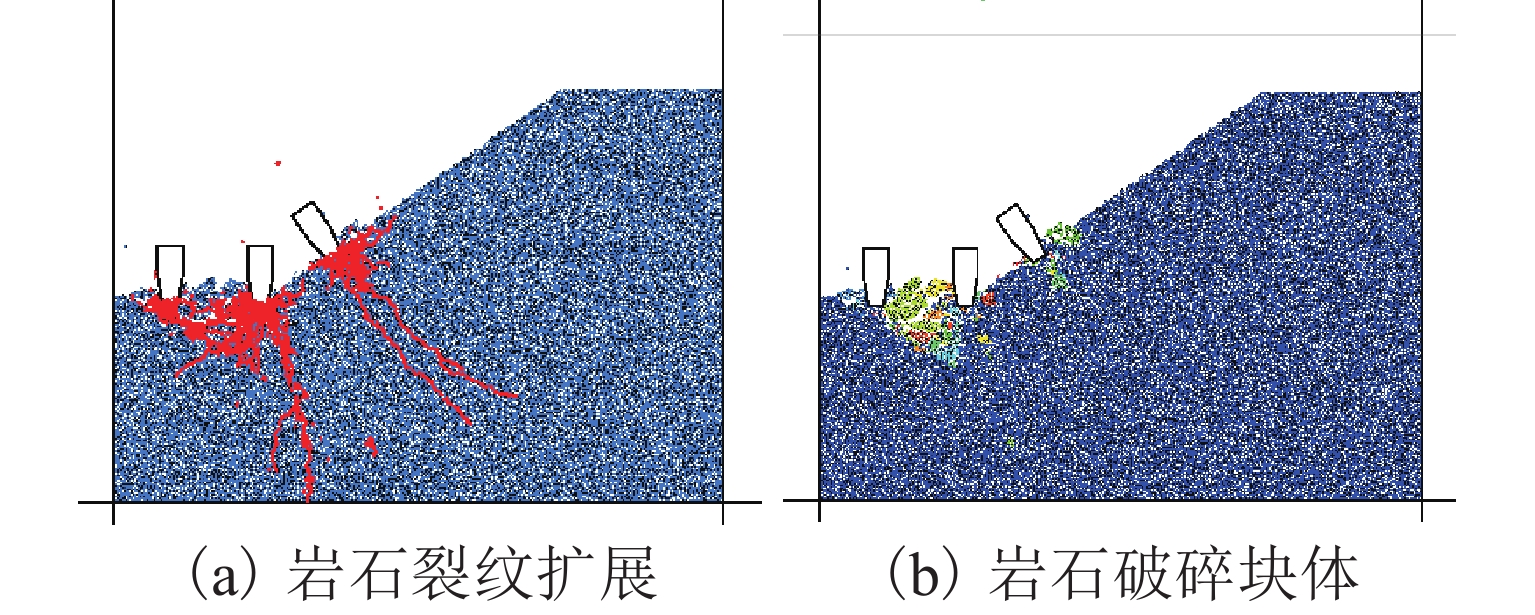
凹陷区域的平面处滚刀刀间距设置为90 mm，锥面处刀间距设置为90 mm，侵入深度设置为15 mm，得到岩石裂纹扩展图和破碎块体图如图5. 当滚刀下压产生的载荷超过岩石的抗压强度后，3把滚刀对岩石产生挤压，力链呈散射状分布. 平面处相邻2把滚刀下压产生的裂纹相互贯通，形成共同破碎区域，破碎区域内颗粒链接破坏，力链传递作用消失；锥面处两把滚刀下压产生的裂纹未形成贯通，无共同破碎区域，中间部分岩石形成岩脊，滚刀破碎效果差. 平面处2把滚刀共同破碎区域和岩石节理处岩渣成块状分布，岩石节理的存在限制了颗粒之间力的传导，导致力链在节理位置明显减弱，同时阻碍了岩石破碎裂纹的扩张，使大部分裂纹沿着节理面延伸，无法向临空面发展.
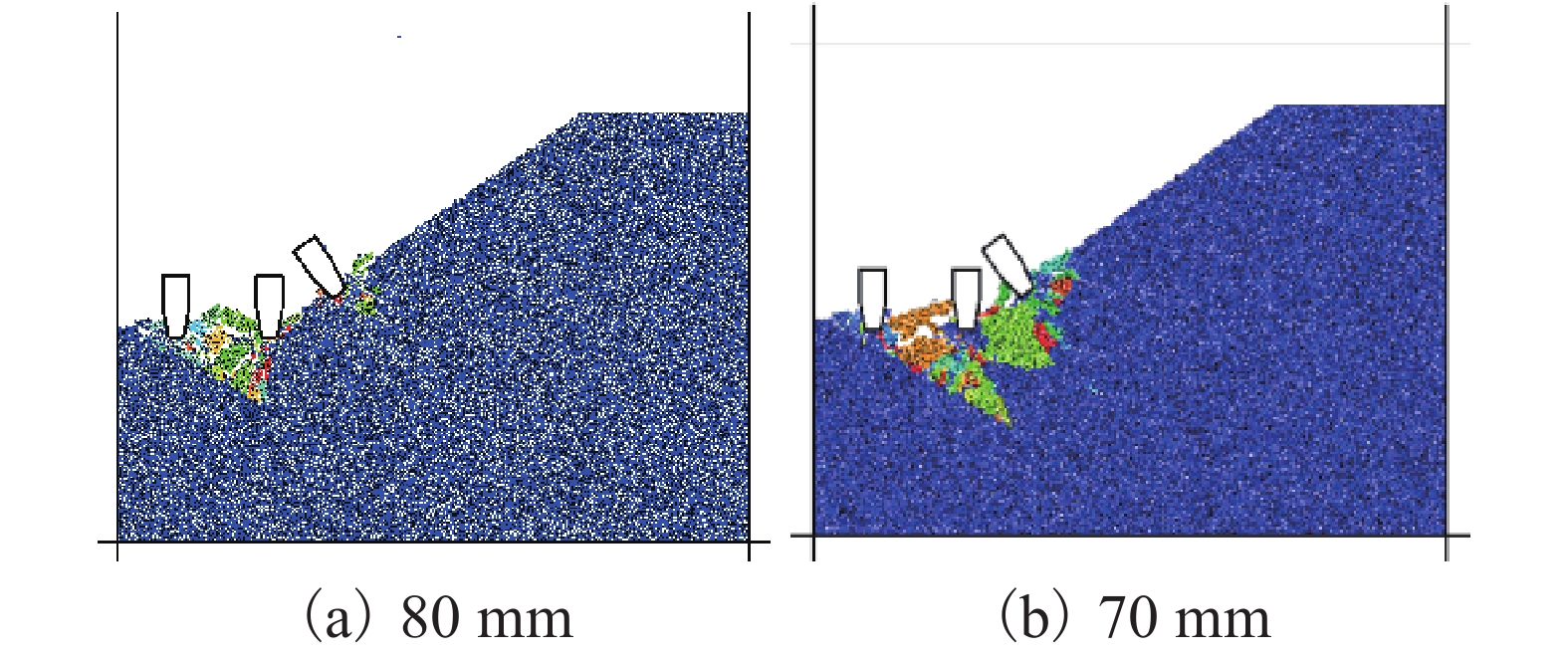
图 5 凹陷区域处90 mm刀间距破岩效果Figure 5. Rock breaking effect of cutters with 90 mm cutter spacing at depression area凹陷区域锥面处刀间距分别设置为80 mm和70 mm，破岩效果如图6所示.
图 6 凹陷区域处不同刀间距破岩效果Figure 6. Rock breaking effect of cutters with different cutter spacing at depression area由图5、6可知：凹陷区域的锥面处刀间距设置为80 mm和90 mm时，由于安装位置的限制，平面处及锥面处均采用双刃盘形滚刀，平面处滚刀与锥面处滚刀的中心线存在夹角，导致两滚刀刀刃不处于同一平面，协同破岩效果较差，未形成共同破碎区域；当凹陷区域锥面处刀间距设置为70 mm时，破碎效果较刀间距设置为90 mm和80 mm时更好. 由于凹陷区域锥面处岩石破碎情况的改变，减小了中间滚刀所受的岩石挤压力，平面处2把滚刀破碎岩石区域增大，破碎效率增加. 因此应该缩小凹陷区域处滚刀组的布刀间距，千枚岩地层下两滚刀布刀间距建议采用70 mm，凹陷区域处滚刀协同破岩效果较好.
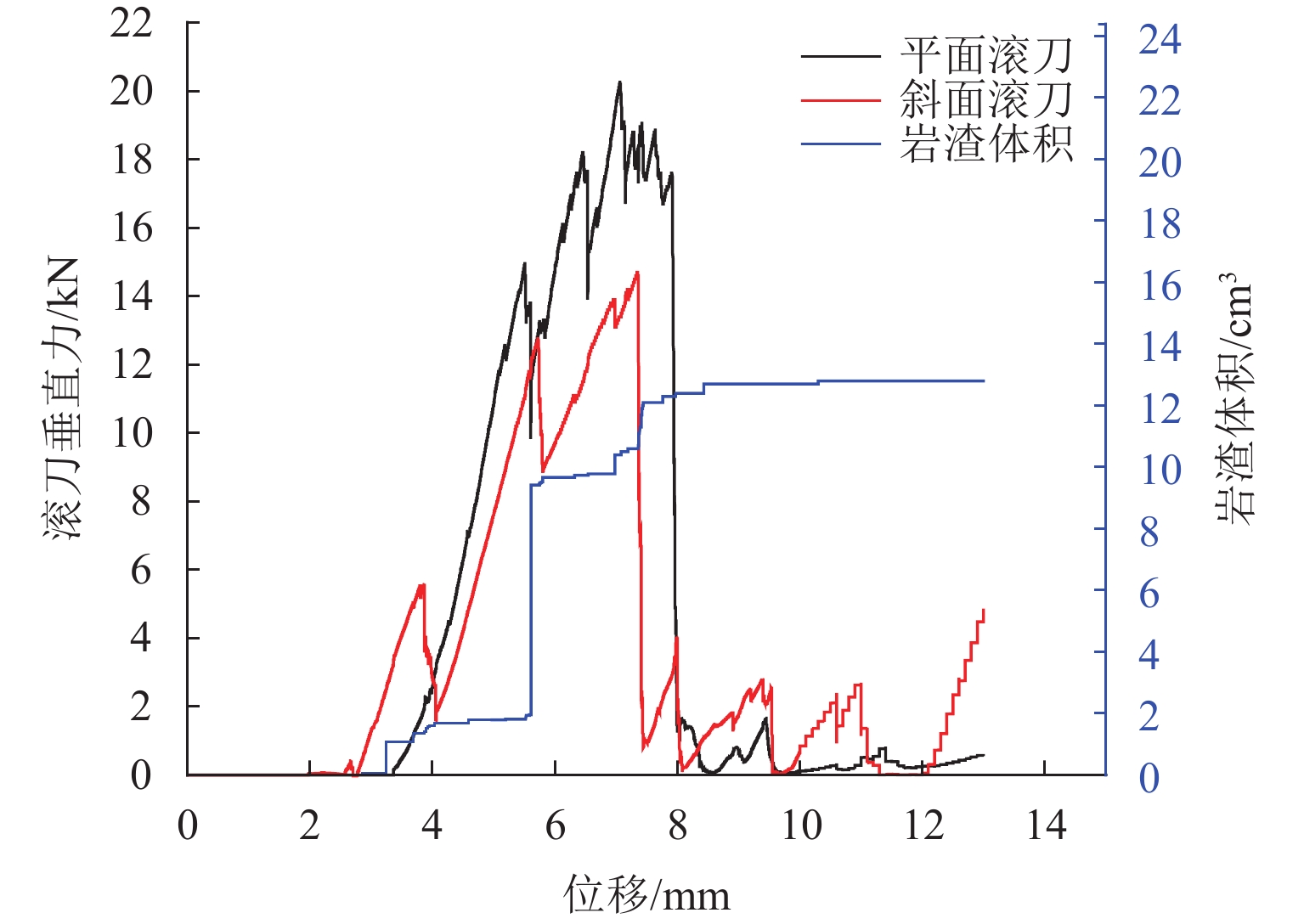
凹陷区域处不同刀间距滚刀破岩时，随着贯入深度增加，滚刀垂直力和岩石破碎体积曲线如图7所示. 由于凹陷区域锥面处滚刀垂直于开挖面，在竖井掘进机竖直开挖过程中，相当于其切削岩石的刀刃宽度变小，在滚刀所受垂直力变化规律上表现为正面滚刀所受垂直力比锥面滚刀更大. 但其可能会产生刀具偏磨或加剧轴承损坏等不良影响，因此，锥面处滚刀的安装布局需综合考虑载荷、破岩效率等因素.
图 7 滚刀垂直力和破岩体积变化规律Figure 7. Variation law of vertical force and rock breaking volume of cutters2.3 刀盘锥面处滚刀刀间距对破岩的影响
为探究异型刀盘锥面处滚刀刀间距对破岩的影响，设锥面处滚刀安装倾角设置为0° （滚刀垂直于锥面安装），贯入度设置为15 mm，根据式（1）将刀间距分别设为80、90、100、110 mm，共建立4组模型，破岩效果如图8所示.
图 8 不同刀间距的破岩效果图Figure 8. Rock breaking effect of cutters with different cutter spacing由图8可知：刀间距设置为80、90、100 mm，2把滚刀刀刃下方形成的破碎区域相互连接，形成了扁长形的岩屑，2把滚刀之间力链传导消失；刀间距设置为80、90 mm时，2刀刃间的岩屑较小，岩石过度破碎，使得破碎效率降低；刀间距为110 mm的2把滚刀中间的岩石裂纹没有完全贯通，刀刃之间有孤立的岩脊产生，仍有力链分布，2把滚刀各自独立破岩.
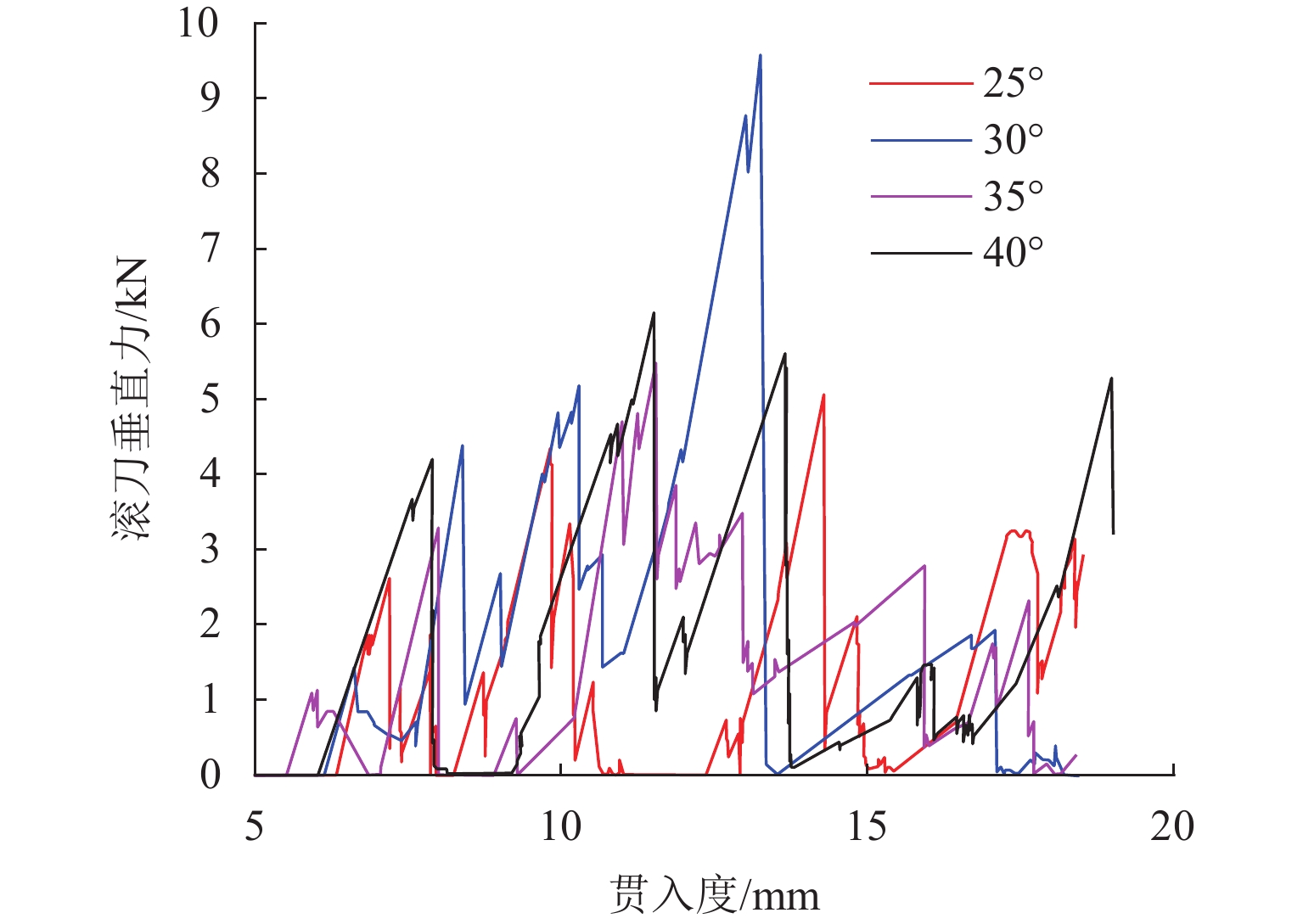
不同刀间距的滚刀组在破岩时，随着其贯入深度的增加，其滚刀垂直力的变化曲线如图9所示. 不同刀间距下滚刀破坏岩石所承受的载荷均为单峰值曲线，80 mm刀间距时滚刀垂直力峰值最小，100 mm刀间距时滚刀垂直力峰值最大. 刀间距越大，两滚刀之间的协同破岩作用越小，单把滚刀所需承受的载荷越大，在破碎区域形成后，相邻刀刃周围岩石内残余的胶结力越小，后续密实所需载荷越小；刀间距越小，2把滚刀之间的协同破岩作用越大，但相邻滚刀间岩石会产生过度破碎，破碎效率低，周围岩石内部应力更为集中，所形成的密实内核导致滚刀垂直力波动较大. 整体规律表现为：在侵入岩石前半段，滚刀间距大的所受载荷更大，在侵入岩石后半段，滚刀间距小的后续载荷波动更大. 仿真分析所得载荷变化规律与CSM （Colorado School of Mines）模型的理论分析[20]相吻合，也与文献[9，21]的滚刀垂向力载荷规律特征相同，即4种刀间距下滚刀破岩受到的垂直力都随时间出现上下波动的变化，体现出滚刀受力的阶跃性变化特征，验证了仿真的合理性.
破碎效率是衡量滚刀破碎岩石的重要指标，其计算方式目前由统一的破岩比能来表达. 由于属于二维仿真，滚刀破岩的滚动力无法监测，盘形滚刀的破岩比能SE可通过式（2）求得[22].
SE=Fvh/V， (2) 式中： V为岩石破碎体积，m3.
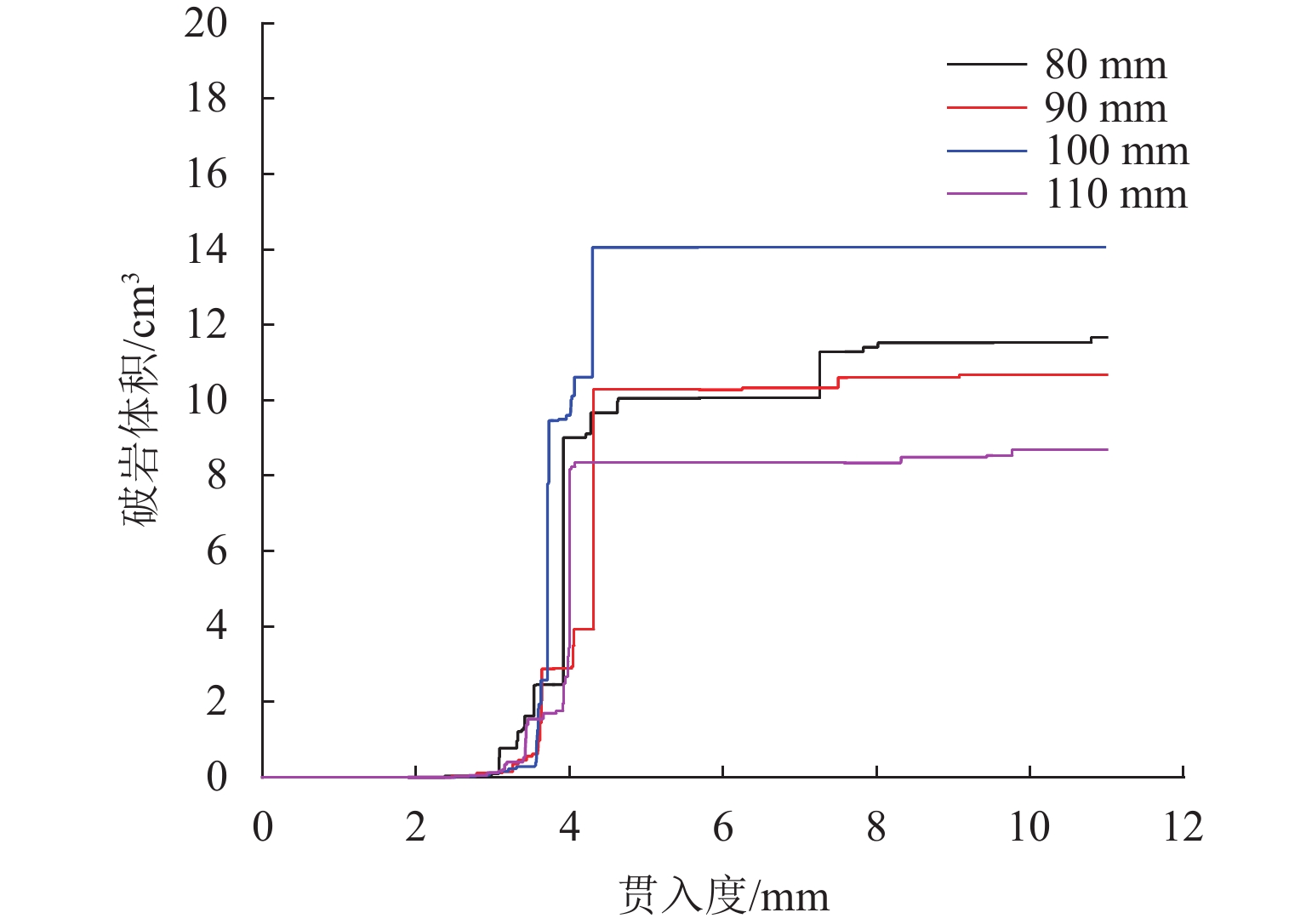
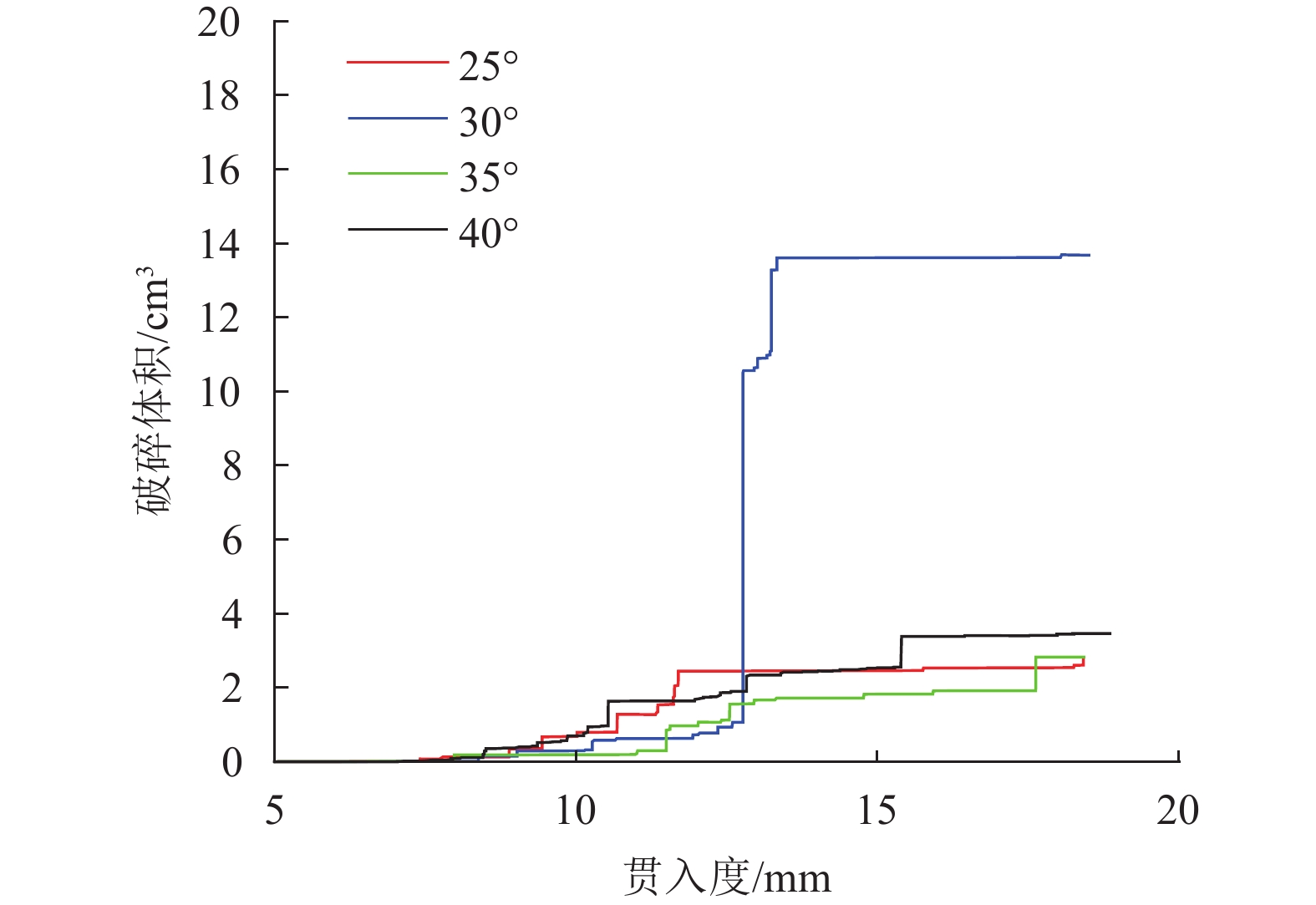
破岩体积由hist函数监测得到，随着贯入深度的增加，不同刀间距的破岩体积如图10所示. 当刀间距为100 mm时，破岩体积最大.
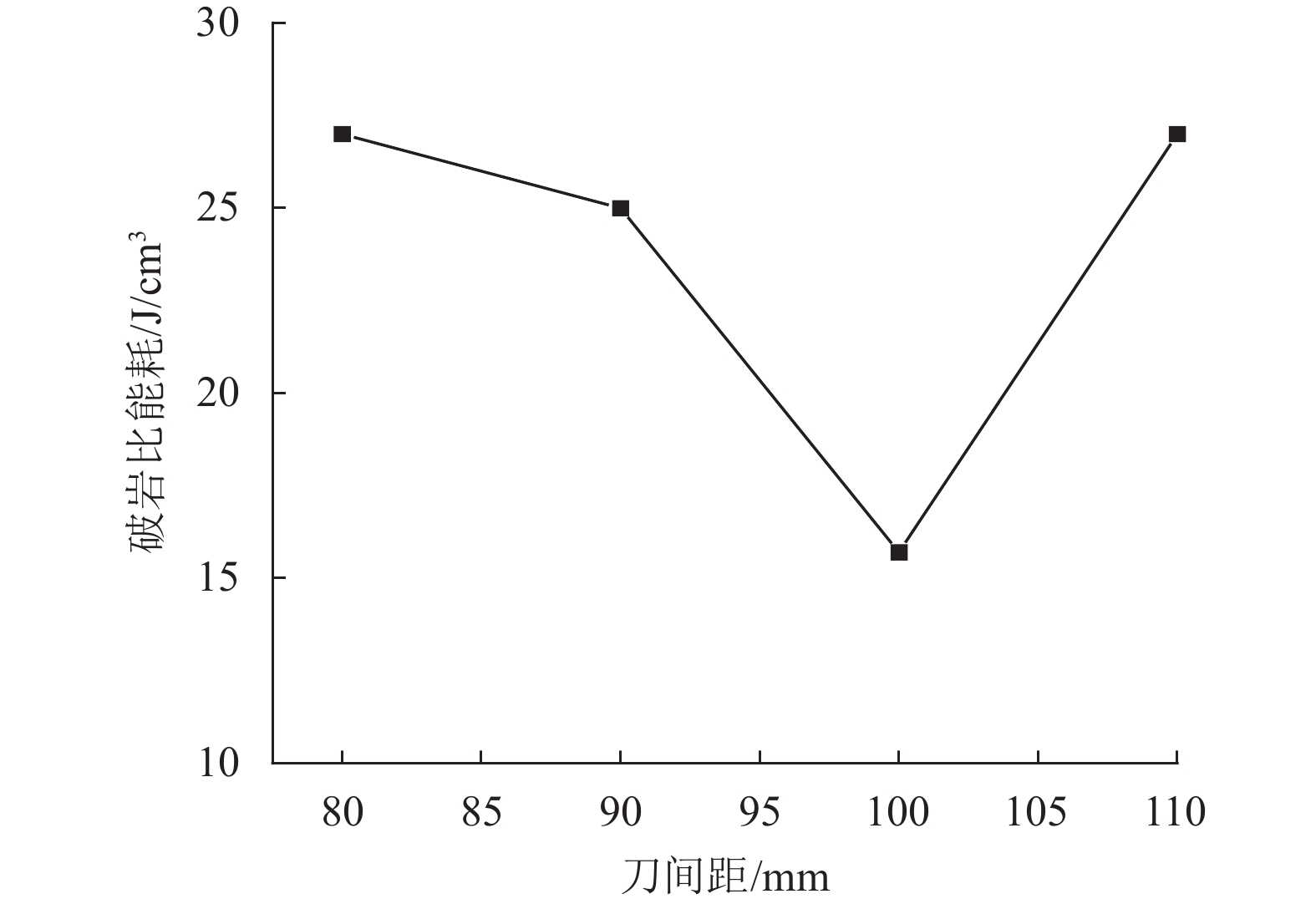
图 10 不同刀间距的破岩体积Figure 10. Rock breaking volume of cutters with different cutter spacing破岩过程中滚刀垂直力处于波动状态，不为恒定值，滚刀破岩垂直力随侵入深度变化的曲线与横轴围成的面积，即为单把滚刀垂直力所做的功，可求得各刀间距下滚刀垂直力所做的功分别为290、288、221、292 J，代入式（2）求得不同刀间距下的破岩比能，如图11所示. 当滚刀间距为100 mm时，破碎单位体积岩石所消耗的能量最低，为15.4 J/cm3，破岩效率最高，可为竖井掘进机异型刀盘的滚刀布局提供参考.
图 11 不同刀间距的破岩比能Figure 11. Specific energy of rock breaking of cutters with different cutter spacing2.4 刀盘锥面处滚刀安装倾角对破岩的影响
滚刀破岩的安装倾角为滚刀刀刃法向矢量与开挖掌子面法向矢量间形成的夹角. 为探究异型刀盘锥面处滚刀安装倾角对破岩的影响，锥面处滚刀刀间距设置为100 mm，贯入度设置为15 mm，安装倾角分别设置为25°、30°、35°、40°，共建立4组模型. 岩石尺寸参数、滚刀结构均与3.3节相同，其中30°相当于滚刀垂直岩石节理破岩，35° 相当于滚刀在刀盘锥面上竖直安装，与重力方向一致.
各倾角破岩效果如图12所示. 由图可知：1） 从裂纹分布来看，滚刀破岩产生的裂纹主要朝2个方向扩展，一是平行于节理倾角的方向，二是垂直于节理倾角的方向；4种角度均形成了协同破岩区域，2把刀刃间形成的岩屑为扁长条；力链分布图中两滚刀刃之间力的传导减弱，表明中部岩石胶结已被破坏形成岩渣. 2） 从岩石的破碎形态来看，滚刀垂直破岩与形成倾角的滚刀破岩相比，前者破岩效果更好.
图 12 不同安装倾角的破岩效果图Figure 12. Rock breaking effect of cutters with different tilt angles随着贯入度的增加，不同安装倾角的滚刀垂直力如图13所示. 由图13可知：安装倾角为30° 时，滚刀垂直力峰值最大，35° 时滚刀垂直力峰值最小；安装倾角为30° 时，滚刀刀刃法向垂直节理倾角方向，滚刀压力载荷无法向其余裂隙面卸压，导致其滚刀垂直力比其余破岩倾角下的数值大，在突破峰值以后，即裂纹扩展到节理面，滚刀垂直力骤降，且后续波动值小于其余破岩倾角下的滚刀垂直力；安装倾角为35° 时，滚刀破岩方向与重力方向一致，滚刀的垂直力直接作用于岩石，侧向力较小，所以其垂直力峰值最小.
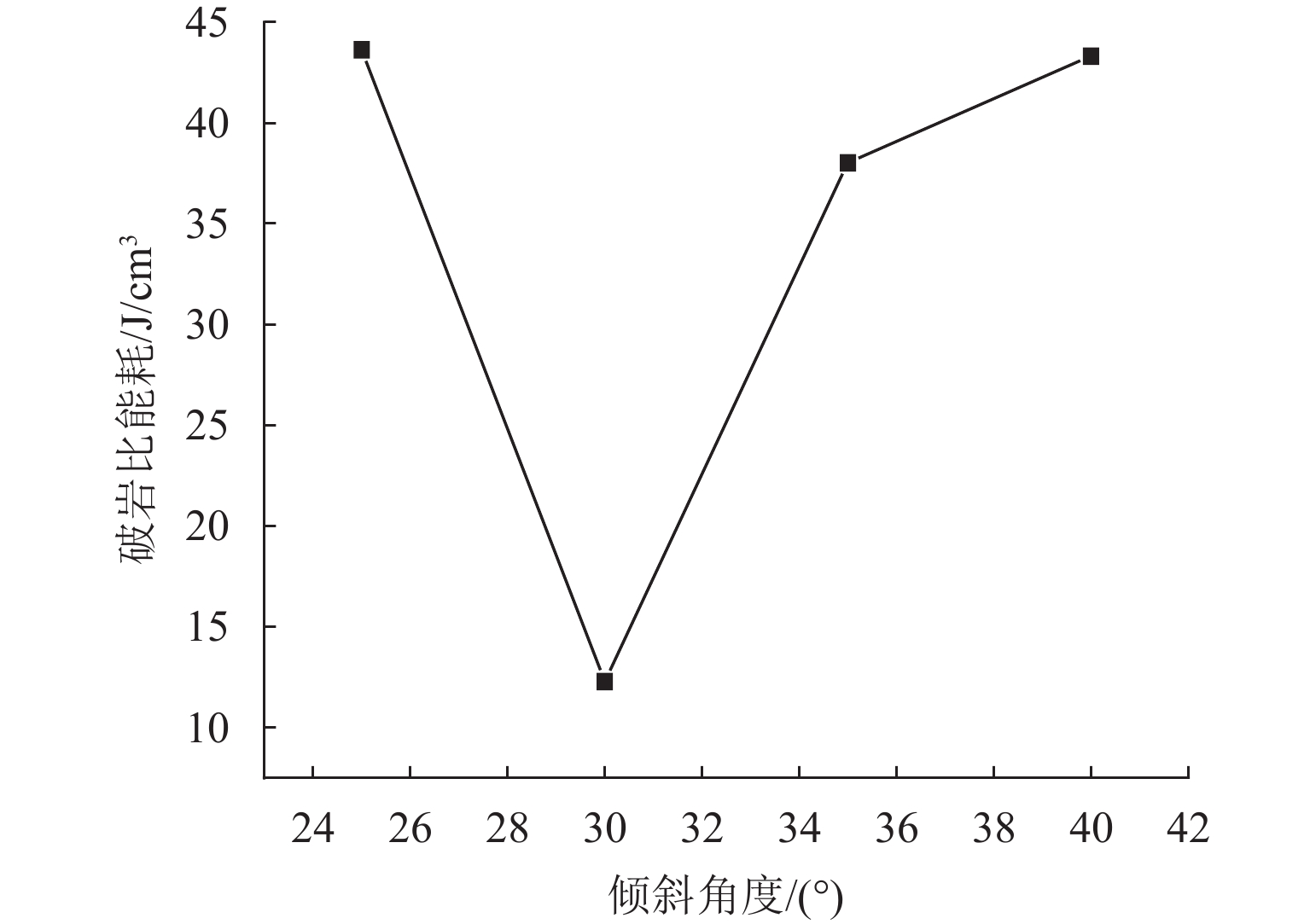
不同安装倾角的岩石破碎体积如图14所示. 滚刀安装倾角为30° 的岩石破碎体积与滚刀垂直锥面安装的岩石破碎体积基本相同，远大于以其余安装倾角布局时的岩石破碎体积，原因是岩石裂纹扩展到了节理面，与节理面形成共同破碎大块岩石. 同理，将滚刀所做的功以及岩石破碎体积代入式（2）中，得到不同安装倾角下破岩比能如图15所示. 由图15可知：安装倾角为30° 时的破岩比能为12.3 J/cm3，与垂直锥面破岩比能为15.4 J/cm3相比，所消耗能量相差较小；与安装倾角为35° 的破岩比能38.0 J/cm3相比，安装倾角为30° 时滚刀破岩所消耗的能量要远小于安装倾角为35°.
图 14 不同倾角的岩石破碎体积Figure 14. Rock breaking volume of cutters with different tilt angles
图 15 不同倾角的破岩比能Figure 15. TSpecific energy of rock breaking of cutters with different tilt angles工程中岩石节理方向随着竖井掘进深度的增加而不断变化. 由图15可知，当滚刀垂直岩石节理破岩时，破岩比能最小. 当滚刀不垂直岩石节理破岩时，即使相差5° 的破岩比能也远大于滚刀垂直岩石节理的破岩比能. 目前掘进机的滚刀安装工艺通常使用滚刀垂直锥面和滚刀竖直安装2种方式，相对于带倾角的滚刀安装方式，更有利于保证滚刀的安装精度. 综上所述，通过分析裂纹分布、滚刀载荷、破岩体积、比能及滚刀安装工艺，建议刀盘锥面处合理的滚刀安装方式为滚刀垂直锥面安装，研究结果可为异型刀盘的滚刀布局提供参考.
3. 滚刀整体布局方案
3.1 滚刀布局方式
滚刀布局方式主要有螺旋线型、星型和随机型3种. 根据盾构/TBM平面刀盘的刀具布局设计及工程经验，3种滚刀布局模型均适合硬岩地层[23]. 竖井全断面掘进机异型刀盘在刀具布局和排渣结构布局上，应优先满足聚排渣性能要求以及排渣结构的空间布局要求. 螺旋线布局模式会使刀具基本均匀布局在刀盘面板上，刀盘受力更均匀，但斗轮机等排渣结构会与刀具布局位置发生冲突. 随机型布局模式的设计难度较高且计算量大，已经较少应用于刀具布局中，因此应按星型方式布刀，采用等刀间距设计，可给排渣结构留有足够的布局空间. 结合凹陷区域处布刀间距为70 mm，锥面处滚刀刀间距为100 mm和滚刀垂直锥面安装的研究成果，得到类“W”型刀盘的滚刀布局，如图16所示.
该异型刀盘上共布局38把滚刀，其中刀位号S1～S6为6把中心滚刀，刀位号S7～S10为4把平面滚刀，均为双刃滚刀. 刀位号S11～S38为锥面滚刀，其中S11、S12、S33和S34为双刃滚刀，其余均为单刃滚刀.
3.2 滚刀布局优化模型
异型刀盘掌子面凹陷区域处对称安装2个斗轮机，其重量相对刀盘中心受力平衡，斗轮机排渣时主要受到铲渣的剪切力，其由斗轮机驱动电机平衡，故滚刀布局的优化只考虑斗轮机的空间影响. 建立滚刀布局优化模型的流程如下：
1） 模型变量设计
全断面竖井掘进机异型刀盘的滚刀布局主要的设计变量有滚刀的布局极径、布局极角、滚刀安装倾角和滚刀超出刀盘的高度. 滚刀安装倾角已确定为垂直掌子面安装，通常滚刀超出刀盘的高度已确定好，所以建立以滚刀在刀盘上的布置极径ρ和布置极角θ为设计变量的多目标优化模型. 边缘滚刀位于刀盘的过渡圆弧上，同时锥面滚刀位于一定角度的锥面上，引入γ和α来分别描述边缘滚刀的安装倾角和锥面滚刀的斜角，γ, α∈[0, π/2].
2） 模型目标函数
采用粒子群优化（PSO）算法[24]，即通过粒子在解空间中的不断迭代找到所求目标的最优解. 滚刀布局需满足以下原则和技术要求[25-26]：① 刀间距合理原则；② 刀盘受力平衡原则，最小化径向载荷和最小化倾覆力矩；③ 滚刀的安装不影响刀盘上其他部件的功能；④ 各滚刀总的质心应接近刀盘回转中心；⑤ 相邻滚刀连续顺次破岩；⑥ 滚刀布刀位置不干涉；⑦ 滚刀寿命相近. 因此，选择最小化径向载荷、最小化倾覆力矩和最小破岩量方差作为竖井全断面掘进机刀盘上滚刀优化布局的目标函数.
3） 模型约束条件
滚刀进行布局计算时还需要满足多个滚刀布局要求，即顺次破岩要求、质心分布要求、刀间距要求和刀具安装不干涉要求，故将滚刀布局要求作为竖井掘进机异型刀盘上滚刀布局优化的约束条件.
3.3 滚刀整体布局优化方案
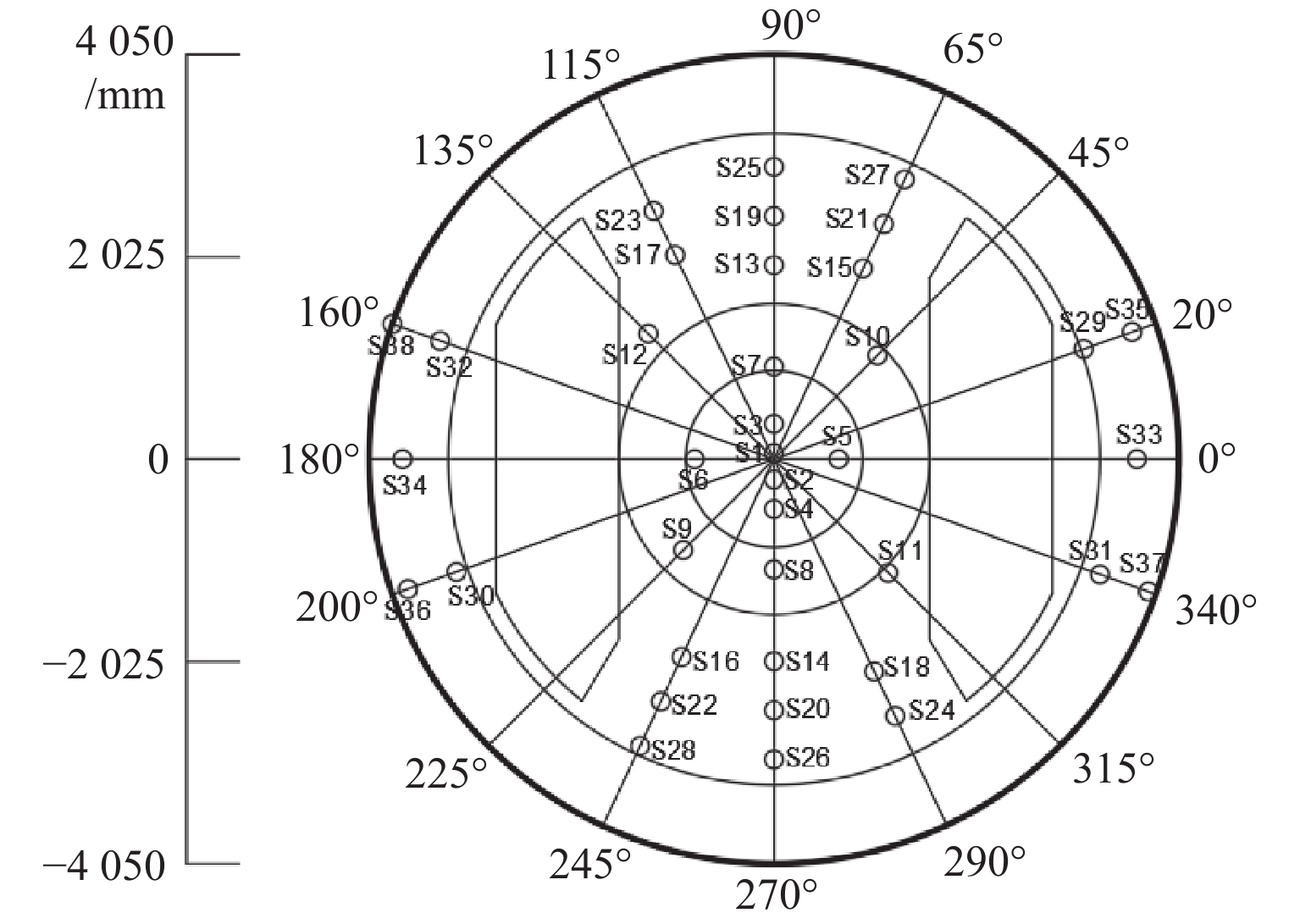
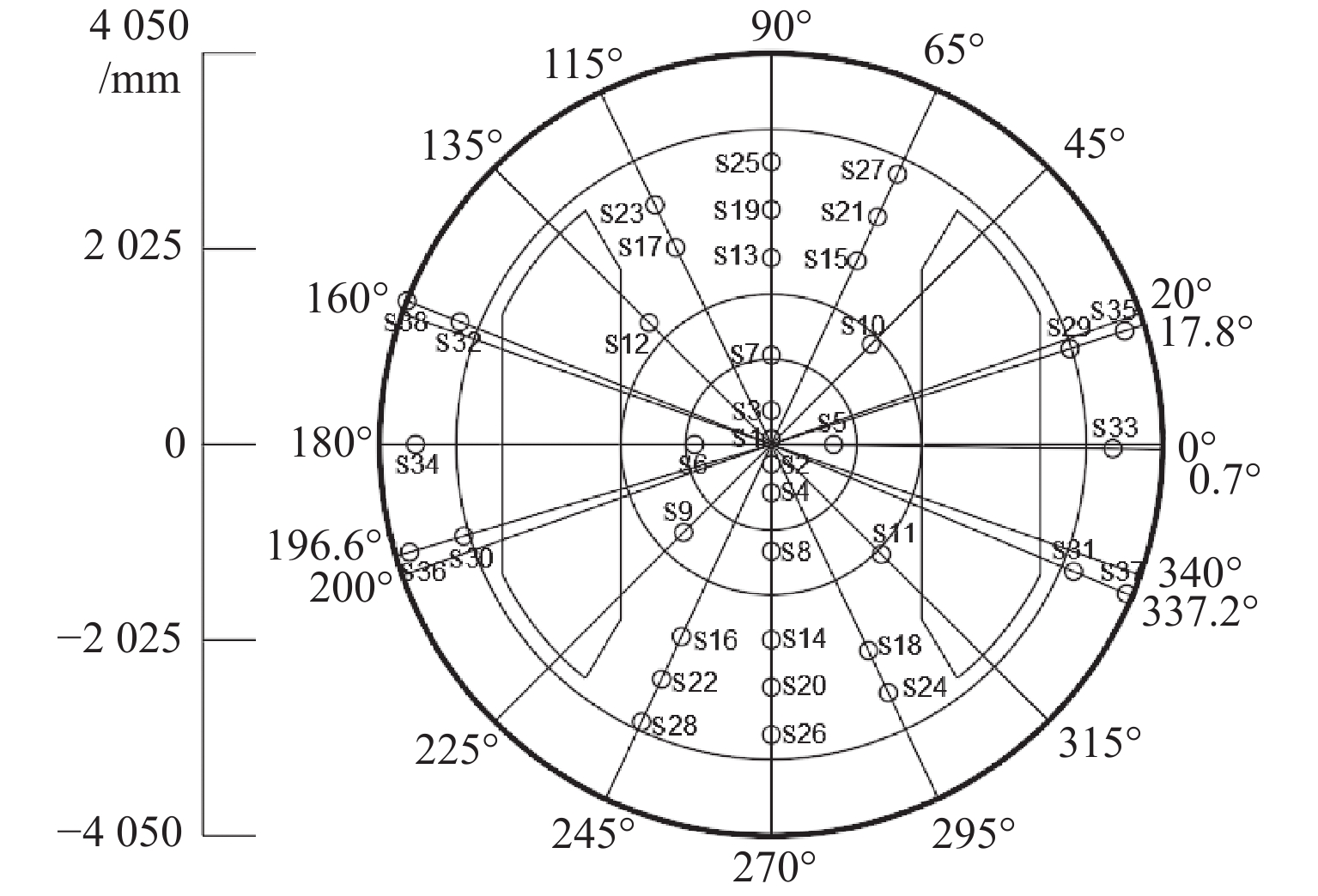
结合图16的异型刀盘上滚刀布局方案，利用粒子群优化（PSO）算法对刀盘凹陷区域及锥面的滚刀S11～S38位置进行优化，未优化部分刀具布局的参数如表3所示. 其中对滚刀S11～S28只进行极径的优化，S29～S38进行极径和极角的优化，优化前后刀具布局参数如表4所示，优化后滚刀布局方案如图17所示.
表 3 未优化的部分刀具布局参数Table 3. Partial cutter layout parameters not involved in optimization滚刀刀号 极径/mm 极角/（°） S1 57.34、130.66 90.0 S2 204.38、278.10 270.0 S3 351.82、425.54 90.0 S4 499.26、572.98 270.0 S5 646.70、720.42 0 S6 794.14、867.86 180.0 S7 925.20、 1015.20 90.0 S8 1105.20 、1195.20 270.0 S9 1285.20 、1375.20 225.0 S10 1465.20 、1555.20 45.0 滚刀布局优化前、后异型刀盘的径向载荷、刀盘合力矩和破岩方差的计算结果如表5所示.
表 5 优化前后各目标函数的对比Table 5. Comparison of objective functions before and after optimization目标函数 径向载荷/N 刀盘合力矩/
（×109 N•m）破岩量方差/
（ ×105 mm3）原刀盘 446.19 3.5 333.73 优化后 338.88 2.1 333.68 由表5可知：优化后刀盘的径向载荷减小24.07%，刀盘合力矩减少40.83%. 径向载荷和刀盘合力矩的优化程度较好，破岩量方差优化结果不太显著. 原因是破岩量方差只与滚刀的布局极径相关，而优化后的刀盘布局中滚刀的布局极径变化不大，破岩量方差优化结果不显著，但是总的优化结果较为成功，满足优化设计要求.
表 4 优化前、后滚刀布局参数Table 4. Partial cutter layout parameters before and after optimization滚刀刀号 优化前 优化后 极径/mm 极角/
（°）极径/mm 极角/
（°）S11 1612.54 、1694.46 315.0 1609.30 、1695.90 315.0 S12 1776.38 、1858.30 135.0 1781.80 、1859.30 135.0 S13 1940.22 90.0 1932.80 90.0 S14 2022.14 270.0 2021.10 270.0 S15 2104.06 65.0 2098.50 65.0 S16 2185.98 245.0 2194.50 245.0 S17 2267.90 115.0 2265.10 115.0 S18 2349.82 295.0 2357.60 295.0 S19 2431.74 90.0 2432.20 90.0 S20 2513.66 270.0 2511.30 270.0 S21 2595.58 65.0 2599.70 65.0 S22 2677.50 245.0 2680.50 245.0 S23 2759.42 115.0 2755.90 115.0 S24 2841.34 295.0 2845.40 295.0 S25 2923.26 90.0 2924.40 90.0 S26 3005.18 270.0 3008.80 270.0 S27 3087.10 65.0 3085.50 65.0 S28 3169.02 245.0 3171.00 245.0 S29 3242.74 20.0 3245.20 17.8 S30 3316.46 200.0 3318.40 196.6 S31 3390.18 340.0 3392.80 337.2 S32 3463.90 160.0 3460.00 158.5 S33 3537.62 （3611.34 ）0 3535.50 （3611.30 ）−0.7 S34 3685.06 （3758.78 ）180.0 3678.30 （3751.20 ）180.0 S35 3832.50 20.0 3839.80 17.8 S36 3906.22 200.0 3903.50 196.6 S37 3979.94 340.0 3985.80 337.2 S38 4050.00 160.0 4050.00 158.5 4. 结 论
1） 竖井全断面掘进机类“W”型刀盘在掌子面凹陷区域处应该缩小布刀间距，千枚岩地层下当布刀间距选取为70 mm时，凹陷区域处滚刀协同破岩效果较好.
2） 以最小破岩比能为指标得到千枚岩地层下异型刀盘锥面处滚刀刀间距为100 mm，通过综合裂纹分布、滚刀载荷、破岩体积、比能及滚刀安装工艺，确定异型刀盘锥面处滚刀适合采取垂直锥面的安装方式.
3） 采用斗轮机排渣方式的竖井全断面掘进机异型刀盘适合采用星型布局方式，在结合高效破岩的滚刀刀间距及安装倾角参数的基础上，采用粒子群优化算法可为国内首台千米硬岩竖井全断面掘进机异型刀盘提供合理的滚刀布局优化方案.
-
图 8 地中测点沉降与支护压力关系曲线
Figure 8. Relationship between subsurface settlement and support pressure
图 10 典型横断面上地层变形情况
Figure 10. Typical vertical displacement curve at transverse profile
图 12 地表测点沉降与支护压力关系曲线
Figure 12. Relationship between surface settlement and support pressure
图 14 地中沉降槽宽度参数随深度比的变化
Figure 14. Width parameter of subsurface settlement trough versus buried depth ratio
图 15 C/D=2.0掌子面前方应力沿隧道埋深重分布(y=0.5D)
Figure 15. Stress redistribution at C/D=2.0 along buried depth in front of tunnel face (y=0.5D)
图 16 C/D=4.0掌子面前方应力沿隧道埋深重分布(y=0.5D)
Figure 16. Stress redistribution at C/D=4.0 along buried depth in front of tunnel face (y=0.5D)
表 1 PFC3D细观力学参数
Table 1. Calibrated PFC3D microscopic parameters
砂
土粒径
分布/cm法向刚度/
(N·m-1)切向刚度/
(N·m-1)颗粒密度/
(kg·m-3)摩擦
因数1# 8~12 7.0×107 7.0×107 2 400 0.80 2# 15~20 7.5×107 7.5×107 2 500 0.85 
下载: 导出CSV
表 2 不同埋深条件下掌子面极限支护压力
Table 2. Limit support pressure under various C/D
C/D 0.5 1.0 2.0 4.0 pf/kPa 7.5 9.0 10.0 10.5
下载: 导出CSV
表 3 不同埋深条件下地表位移突增时的支护压力
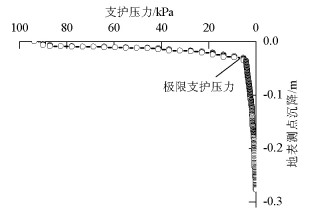
Table 3. pk under various C/D
C/D 0.5 1.0 2.0 4.0 pk/kPa 6.5 6.0 4.5 4.0
下载: 导出CSV
-
MURAYAMA S, ENDO M, HASHIBA T, et al. Geotechnical aspects for the excavating performance of the shield machines[C]//The 21st Annual Lecture in Meeting of Japan Society of Civil Engineers. Tokyo: [s.n.], 1966: 134-140. KRAUSE T. Schildvortrieb mit flüsigkeits-und erdgestüzter ortsbrust[D]. Brunswick: Technical University Carolo Wilhelmina, 1987. HORN N. Horizontal earth pressure on the vertical surfaces of the tunnel tubes[C]//National Conference of the Hungarian Civil Engineering Industry. Budapest: [s.n.], 1961: 7-16. ANAGNOSTOU G, KOVÁI K. Face stability condition with earth pressure balanced shields[J]. Tunnelling and Underground Space Technology, 1996, 11(2):165-73. doi: 10.1016/0886-7798(96)00017-X BROERE W. Tunnel face stability and new CPT application[D]. Delft: Delft University, 2001. ATKINSON J H, POTTS D M. Stability of a shallow circular tunnel in cohesionless soil[J]. Geotechnique, 1977, 27(2):203-215. doi: 10.1680/geot.1977.27.2.203 DAVIS E H, GUNN M J, MAIR F R, et al. The stability of shallow tunnels and underground openings in cohesive material[J]. Geotechnique, 1980, 30(4):397-416. http://www.nrcresearchpress.com/servlet/linkout?suffix=refg6/ref6&dbid=16&doi=10.1139%2Ft11-078&key=10.1680%2Fgeot.1980.30.4.397 LECA E, DORMIEUX L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material[J]. Geotechnique, 1990, 40(4):581-606. doi: 10.1680/geot.1990.40.4.581 MOLLON G, DIAS D, SOUBRA A H. Face stability analysis of circular tunnels driven by a pressurized shield[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(1):215-229. doi: 10.1061/(ASCE)GT.1943-5606.0000194 CHAMBON P, CORTÉ J F. Sallow tunnels in cohesionless soil:stability of tunnel face[J]. Journal of Geotechnical Engineering, 1994, 120(7):1148-1164. doi: 10.1061/(ASCE)0733-9410(1994)120:7(1148) KIRSCH A. Experimental investigation of the face stability of shallow tunnels in sand[J]. Acta Geotechnica, 2010, 5(1):43-62. doi: 10.1007/s11440-010-0110-7 IDINGER G, AKLIK P, WU W, et al. Centrifuge model test on the face stability of shallow tunnel[J]. Acta Geotechnica, 2011, 6(2):43-62. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a70c6918dc14459f22917a817382e04d CHEN R P, LI J, KONG L G, et al. Experimental study on face stability of shield tunnel in sand[J]. Tunnelling and Underground Space Technology, 2013, 33(1):12-21. http://www.sciencedirect.com/science/article/pii/S0886779812001447 VERMEER P A, RUSE N M, MARCHER T. Tunnel heading stability in drained ground[J]. Felsbau, 2002, 20(6):8-18. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CC0211513617 LI Y, EMERIAULTB F, KASTNERB R, et al. Stability analysis of large slurry shield-driven tunnel in soft clay[J]. Tunnelling and Underground Space Technology, 2009, 24(4):472-481. doi: 10.1016/j.tust.2008.10.007 CUNDALL P A, STRACK O D. A discrete numerical model for granular assemblies[J]. Géechnique, 1979, 29(1):47-65. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1208.0565 王俊, 何川, 封坤, 等.砂卵石地层中大断面泥水盾构泥膜形态研究[J].现代隧道技术, 2014, 51(6):108-113. http://d.old.wanfangdata.com.cn/Periodical/xdsdjs201406018WANG Jun, HE Chuan, FENG Kun, et al. Research on the dynamic behavior of the slurry membrane of a large-section slurry shield in a sandy cobble stratum[J]. Modern Tunnelling Technology, 2014, 51(6):108-113. http://d.old.wanfangdata.com.cn/Periodical/xdsdjs201406018 缪林昌, 王正兴, 石文博.砂土盾构隧道掘进开挖面稳定理论与颗粒流模拟研究[J].岩土工程学报, 2015, 37(1):98-104. http://d.old.wanfangdata.com.cn/Periodical/ytgcxb201501011MIU Lingchang, WANG Zhengxing, SHI Wenbo. Theoretical and numerical simulations of face stability around shield tunnels in sand[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(1):98-104. http://d.old.wanfangdata.com.cn/Periodical/ytgcxb201501011 CHEN R P, TANG L J, LING D S, et al. Face stability analysis of shallow shield tunnels in dry sandy ground using the discrete element method[J]. Computers and Geotechnics, 2011, 38(2):187-195. doi: 10.1016/j.compgeo.2010.11.003 MELIS MAYNAR M J, MEDINA RODRIGUEZ L E. Discrete numerical model for analysis of earth pressure balance tunnel excavation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(10):1234-1242. http://www.emeraldinsight.com/servlet/linkout?suffix=b12&dbid=16&doi=10.1108%2F02644400910996862&key=10.1061%2F(ASCE)1090-0241(2005)131%3A10(1234) Itasca Consulting Group Inc. PFC3D (particle flow code in three dimensions) version 4.0 manual[M]. Minneapolis:Itasca Consulting Group Inc, 2001:101-235. MAIR R J, TAYLOR R N, BRACEGIRDLE A. Subsurface settlement profiles above tunnels in clays[J]. Gétechnique, 1993, 43(2):315-320. MAIR R J. Centrifugal modeling of tunnel construction insoft clay[D]. Cambridge: University of Cambridge, 1979. DYER M R, HUTCHINSON M T, EVANS N. Sudden valley sewer: a case history[C]//International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground. London: [s.n.], 1996: 671-676. 期刊类型引用(13)
1. 丁海滨，喻义天，梁禄钜，孙洋，余辉，何建国，徐长节. 基于椭球体理论粘性土层隧道松动土压力研究. 湖南大学学报(自然科学版). 2025(01): 228-238 . 
百度学术2. 肖福坤，谢锴，劳志伟，单磊，刘刚，郝传波. 考虑力链屈服的垮落体中顶进阻力分析. 煤炭学报. 2025(01): 281-296 . 百度学术3. 刘明芳，陈明辉，吴振元，龙桂华. 基于流固耦合的双线盾构隧道施工诱发地表沉降分析. 湖南文理学院学报(自然科学版). 2024(01): 67-75 . 百度学术4. 刘金慧，屈克军，丁万涛，王杨. 硬塑粉质黏土层深埋马蹄形隧道开挖土拱演化分析. 人民长江. 2022(01): 189-197 . 百度学术5. 姜林杰. 基于物元融合云模型的地铁车站下穿建筑物安全风险评价. 四川建材. 2022(01): 219-221 . 百度学术6. 左光恒，倪四清，杨钦. 上覆溶洞影响下高速公路隧道开挖稳定性研究. 粉煤灰综合利用. 2022(01): 64-68 . 百度学术7. 房倩，杜建明，王赶，杨晓旭. 模型边界对圆形隧道开挖引起地表沉降的影响分析. 隧道与地下工程灾害防治. 2022(01): 10-17 . 百度学术8. 徐航，李斌. 砂土地层隧道掌子面的颗粒流模拟. 工程与建设. 2021(01): 77-79 . 百度学术9. 吕涛，李森阔，杨果林，徐浩栋，龙彪. 小半径曲线盾构隧道地面沉降变形特征研究. 水利与建筑工程学报. 2020(04): 198-203 . 百度学术10. 李梓亮，汤劲松，赵书银，姜景双，张宝，郜亮亮. 盾构隧道下穿砌体结构房屋影响因素敏感性分析. 现代城市轨道交通. 2020(10): 85-91 . 百度学术11. 房倩，杜建明，王赶，王中举，王官清. 砂土隧道开挖地层变形规律及影响因素分析. 隧道与地下工程灾害防治. 2020(03): 67-76 . 百度学术12. 牛豪爽，翁效林，余航飞，胡继波. 渗流作用下粉砂地层中盾构隧道开挖面失稳模式离心试验研究. 土木工程学报. 2020(S1): 99-104+118 . 百度学术13. 吴建宾. 偏压小净距公路隧道围岩稳定性与对策研究. 路基工程. 2019(01): 176-179 . 百度学术其他类型引用(15)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 651
- HTML全文浏览量: 303
- PDF下载量: 221
- 被引次数: 28