Air Traffic Flow Prediction Model Based on Improved Adding-Weighted One-Rank Local-rejion Method
-
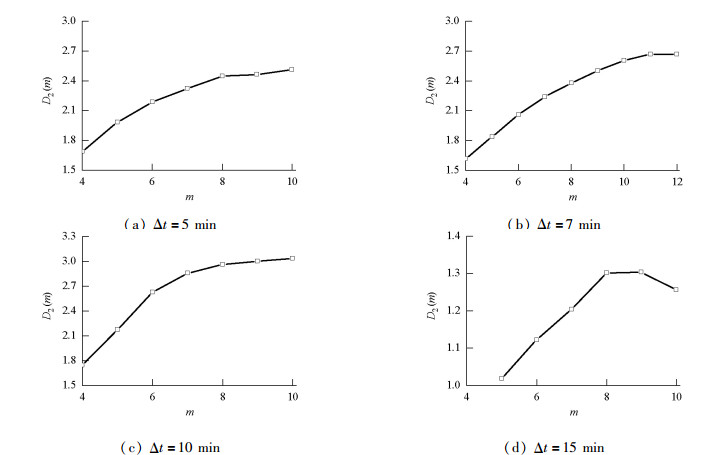
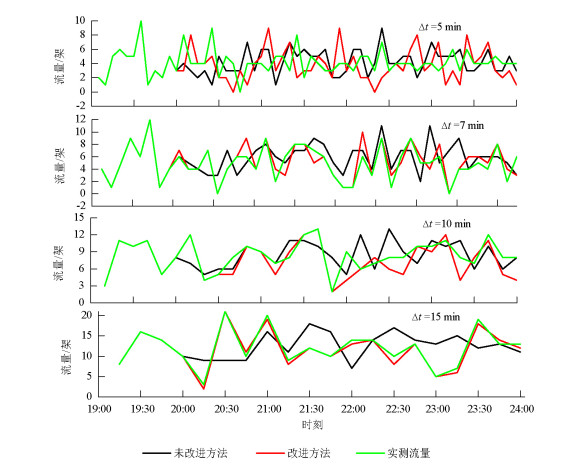
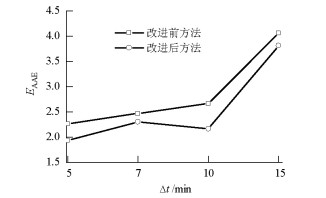
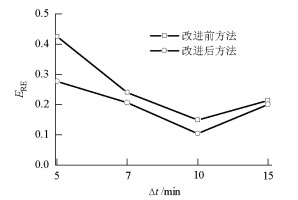
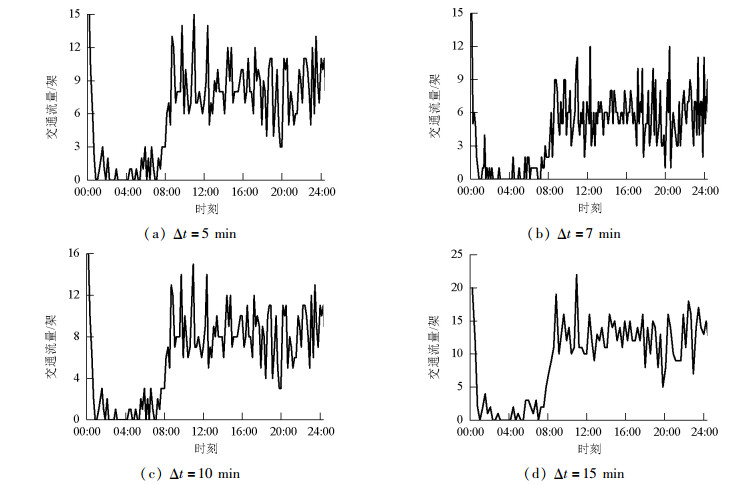
摘要: 空中交通流量精准预测是实施空中交通控制和管理的重要前提.针对空中交通流量时间序列的内在混沌动力特性，研究了基于改进加权一阶局域法的混沌交通流量时间序列预测模型.首先，提出了一种临近相点演化加权的改进一阶局域预测法，并通过在预测过程中构建误差序列进行预测结果修正；其次，利用关联维数出现饱和现象验证了4组不同统计时间间隔的实测空中交通流量时间序列均存在混沌特性；最后，在对空中交通流量时间序列进行相空间重构的基础上，利用改进加权一阶局域预测方法进行了流量预测结果的对比实验.结果表明，4组空中交通流量时间序列预测精度均有提高，时间尺度为10 min的流量预测效果最好，预测相对误差减小了29.7%.Abstract: Accurate air traffic flow prediction is an important basis for efficient air traffic control and management. Aiming at the inherent chaotic dynamic characteristics of air traffic flow time series, the chaotic traffic-flow time-series prediction model based on improved adding-weight one-rank local-region prediction method was analyzed herein. Firstly, an improved adding-weight one-rank local-region prediction method was proposed, which involved weighing the evolution of adjacent phase points. Further, the prediction results were corrected by construction of error sequences during the prediction process. Secondly, the chaotic characteristics were verified to exist in four groups of air traffic flow time series at different time scales, using the saturation phenomenon of correlation dimension. Finally, a validation experiment for air traffic flow prediction was carried out using the improved method, after phase space reconstruction of air traffic flow time series. The results show that the prediction accuracy of all four groups is improved, wherein the traffic flow time series with time scale of 10 min has the best precision; the relative error in this case reduces by 29.7%.
-
图 2 Δt=10 min时的自相关系数函数
Figure 2. The auto correlative function of Traffic flow time series of 10 min
图 6 空中交通流量预测的平均绝对误差对比
Figure 6. Comparison Average absolute error of Air traffic flow prediction
图 7 空中交通流量预测的相对误差对比
Figure 7. Comparison Relative error of Air traffic flow prediction
表 1 不同时间尺度空中交通流量时间序列的时间延迟和嵌入维数
Table 1. Time delay and Embedding dimension of Air traffic flow time series under different time scales
参数 Δt=10 min Δt=7 min Δt=10 min Δt=15 min τ/min 2 3 3 4 m 6 9 7 4 
下载: 导出CSV
-
耿睿, 崔德光, 徐冰.应用支持向量机的空中交通流量组合预测模型[J].清华大学学报:自然科学版, 2008, 48(7):1205-1208. http://d.old.wanfangdata.com.cn/Periodical/qhdxxb200807036GENG Rui, CUI Deguang, XU Bing. Support vector machine-based combinational model for air traffic forecasts[J]. Journal of Tsinghua University, 2008, 48(7):1205-1208. http://d.old.wanfangdata.com.cn/Periodical/qhdxxb200807036 张明, 韩松臣, 黄林源.基于双重力模型和人工神经网络的空中交通流量组合预测[J].西南交通大学学报, 2009, 44(5):764-770. doi: 10.3969/j.issn.0258-2724.2009.05.025ZHANG Ming, HAN Songchen, HUANG Linyuan. Air traffic flow combinational forecast based on double gravity model and artificial neural network[J]. Journal of Southwest Jiaotong University, 2009, 44(5):764-770. doi: 10.3969/j.issn.0258-2724.2009.05.025 王超, 郭九霞, 沈志鹏.基于基本飞行模型的4D航迹预测方法[J].西南交通大学学报, 2009, 44(2):295-300. doi: 10.3969/j.issn.0258-2724.2009.02.028WANG Chao, GUO Jiuxia, SHEN Zhipeng. Prediction of 4D trajectory based on basic flight models[J]. Journal of Southwest Jiaotong University, 2009, 44(2):295-300. doi: 10.3969/j.issn.0258-2724.2009.02.028 吕金虎, 张锁春.加权一阶局域法在电力系统短期负荷预测中的应用[J].控制理论与应用, 2002, 19(5):767-770. http://d.old.wanfangdata.com.cn/Periodical/kzllyyy200205022LÜ Jinhu, ZHANG Suochun. Application of adding-weight one-rank local-region method in electric power system short-term load forecast[J]. Control Theory & Applications, 2002, 19(5):767-770. http://d.old.wanfangdata.com.cn/Periodical/kzllyyy200205022 金玉婷.基于混沌和小波神经网络的短时交通流量预测方法研究[D].成都: 西南交通大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10613-1014251940.htm 陈丹, 胡明华, 张洪海, 等.考虑周期性波动因素的中长期空中交通流量预测[J].西南交通大学学报, 2015, 50(3):562-568. doi: 10.3969/j.issn.0258-2724.2015.03.028CHEN Dan, HU Minghua, ZHANG Honghai, et al. Forecast method for medium-long term air traffic flow considering periodic fluctuation factors[J]. Journal of Southwest Jiaotong University, 2015, 50(3):562-568. doi: 10.3969/j.issn.0258-2724.2015.03.028 张洪海, 杨磊, 别翌荟, 等.终端区进场交通流广义跟驰行为与复杂相变分析[J].航空学报, 2015, 36(3):949-961. http://d.old.wanfangdata.com.cn/Periodical/hkxb201503028ZHANG Honghai, YANG Lei, BIE Yi Hui, et al. Analysis on generalized following behavior and complex phase-transition law of approaching traffic flow in terminal airspace[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3):949-961. http://d.old.wanfangdata.com.cn/Periodical/hkxb201503028 PACKARD N H, CRUTCHFIELD J P, FARMER J D. Geometry from a time series[J]. Physics Review Letters, 1980, 45(9):712. doi: 10.1103/PhysRevLett.45.712 吕金虎, 陆君安, 陈士华.混沌时间序列分析及应用[M].武汉:武汉大学出版社, 2002:102-105. CONG W, HU M H. Chaotic characteristic analysis of air traffic system[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2014, 31(6):636-642. http://www.cqvip.com/QK/85388X/201406/663464141.html LI S M, XU X H, MENG L H. Flight conflict forecasting based on chaotic time series[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2012, 29(4):388-394. http://en.cnki.com.cn/Article_en/CJFDTOTAL-NJHY201204014.htm 王超, 郑旭芳, 王蕾.交汇航路空中交通流的非线性特征研究[J].西南交通大学学报, 2017, 52(1):171-178. doi: 10.3969/j.issn.0258-2724.2017.01.024WANG Chao, ZHENG Xufang, WANG Lei. Research on nonlinear characteristics of air traffic flows on converging air routes[J]. Journal of Southwest Jiaotong University, 2017, 52(1):171-178. doi: 10.3969/j.issn.0258-2724.2017.01.024 STROGATZ S H. Nonlinear dynamics and chaos:with applications to physics, biology, chemistry, and engineering[M]. Boulder:Westview Press, 2014:317-335. XUE J, SHI Z. Short-time traffic flow prediction based on chaos time series theory[J]. Journal of Transportation Systems Engineering & Information Technology, 2008, 8(5):68-72. http://www.sciencedirect.com/science/article/pii/S1570667208600409 LAN L W, SHEU J B, HUANG Y S. Investigation of temporal freeway traffic patterns in reconstructed state spaces[J]. Transportation Research Part C Emerging Technologies, 2008, 16(1):116-136. doi: 10.1016/j.trc.2007.06.006 TAKENS F. On the numerical determination of the dimension of an attractor[M]. Berlin:Springer, 1985:99-106. MAÑÉ R. On the dimension of the compact invariant sets of certain non-linear maps[M]. Berlin:Springer, 1981:230-242. 贺国光, 马寿峰, 冯蔚东.对交通流分形问题的初步研究[J].中国公路学报, 2002, 15(4):82-85. doi: 10.3321/j.issn:1001-7372.2002.04.022HE Guoguang, MA Shoufeng, FENF Weidong. Preliminary study of fractals of traffic flow[J]. China Journal of Highway & Transport, 2002, 15(4):82-85. doi: 10.3321/j.issn:1001-7372.2002.04.022 马庆禄.基于混沌理论的交通状态预测研究[D].重庆: 重庆大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10611-1012047358.htm KANTZ H, SCHREIBER T. Nonlinear time series analysis[M]. Cambridge:Cambridge University Press, 2004:69-72. GRASSBERGER P, PROCACCIA I. Measuring the strangeness of strange attractors[J]. Physica D Nonlinear Phenomena, 1983, 9(1):189-208. http://www.sciencedirect.com/science/article/pii/0167278983902981 -
下载:
点击查看大图
图(7) / 表(1)
计量
- 文章访问数: 458
- HTML全文浏览量: 174
- PDF下载量: 98
- 被引次数: 0